试论如何在小学数学教学中“以学定教”
2017-03-31贾亚健
贾亚健
【摘要】本文针对“以学定教”理念下的教师如何构建和谐课堂教学进行了论述,阐述了教师在设计教学时应当站在学生高度,重视学生的认知需要;要基于学生视角,培养学生的问题意识;要充分预设生成,引导学生深化问题思考。教师应当做到把课堂讲解还给学生、把课堂展示让给学生以及把课堂思辨留给学生,同时,在学生思维短路时点醒学生、在学生方法多样时点拨学生择优、在学生进行认知建构时点化学生。
【关键词】和谐课堂 以学定教 为生设计 还生舞台 点生所惑
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2017)02A-0026-03
数学“和谐课堂”是生本教育理念下“以学定教”的新课堂,体现了高度和谐的师生关系,它改变了传统数学课堂中学生被动仰望教师的现状,真正地化“课堂”为“学堂”。学生在“和谐课堂”上敢于提出问题,畅所欲言地讨论问题,乐于建设性地解决问题,学习状态生机盎然,新思想、新方法不断动态生成。笔者对如何设计“和谐课堂”教学、教师怎样“为生而教”以及学生怎样“展现自我”进行了教学实践与思考。
一、为学生设计
教学应当为学生设计。但实际上,目前教师的教学设计更多的是为教材而设计,为教师的教而设计。“和谐课堂”的教学设计要求教师从学生的高度、角度出发,在动态生成的学情中,关注学生、读懂学生、把握好教学的尺度,及时进行智慧的引领,从而实现弹性的预设,丰富的生成。
(一)站在学生高度,重视认知需要
《义务教育数学课程标准(2011年版)》指出:教师应充分利用学生的生活经验,设计生动有趣、直观形象的数学活动,激发学生的学习兴趣,让学生在生动具体的情境中理解并掌握数学知识。数学“和谐课堂”坚持“以学定教”,教学活动贴着学生的思维行进,尊重学生认知需求,着力帮助学生在认知的过程中弄清楚“是什么”和“为什么”。
蘇教版五年级数学下册《用数对确定位置》,例1出示了5行6列的教室座位图,设计了基于学生认知水平的开放性问题“小军坐在哪里?”学生运用已有的经验,呈现出多种表示方法:第3排第4个、第4组第3个、第3行第4个等,学生并没有意识到是因为观察方向和顺序的不同而导致了表示方法的不确定,因此不会产生“用数对确定位置”的需要。这时教师可站在学生的高度,设计能够造成学生认知冲突的问题,从而激发学生的认知需要,例如,“小军的位置没有变,为什么你们的说法都不一样呢?怎样才能让观察的方法和顺序变得一致?确定位置有没有更简洁的表示方法?”这样的问题基于学生,源于教材,激活了学生的元认知,让学生真实经历数学的发展过程,同时为接下来的研究数对提供了素材。
(二)基于学生视角,培养问题意识
“和谐课堂”是动态的课堂,教师的教学设计要富有弹性,在板块的设计中要树立问题意识,设计开放性的数学活动,有意识地留下探究的入口,创造机会让学生成为问题的发现者,问题的探究者,问题的创造者,引导学生围绕数学的本质进行有针对性的问题思考,引领学生向知识的内核和思维的更深处延伸。
在苏教版数学五年级下册《奇妙的图形密铺》中,教材安排学生操作探究五种平面图形能否独立密铺,学生为实验而实验,缺乏对数学本质的思考。教师可以在操作实验之前设计这样一个问题激发学生主动探究问题:“通过生活中的铺砖现象,我们看到长方形、正方形和正六边形可以密铺,你会联想到其他问题吗?”学生很容易联想到“平行四边形能密铺吗?三角形、梯形呢?是不是平面图形都能密铺?”问题源于学生,学生的实验和思考的热情被调动起来。在学生通过实验发现正五边形不能密铺后,教师又设计了“能激发问题”的问题,引导学生走向思维的深处,如:“正五边形不能密铺,有没有激起你心中的疑问,你想问什么?”学生短暂思考后,接二连三地抛出问题:“正五边形为什么不能密铺?其他直边的平面图形为什么可以密铺?能密铺的图形有什么秘密?密铺究竟和什么有关?……”同伴之间的问题引燃了思维的火花,为接下来探究密铺的奥秘明确了方向。
(三)充分预设生成,深化问题思考
“和谐课堂”教学设计的出发点是学生的学情,而课堂上学生的学情是不断发展,动态生成的,教师要明白动态生成的是学生个性的思考,不变的是知识发展的脉络,所以教师在进行教学设计时要根据学生的学习起点充分预设,合理把握学生的动态生成,及时调整教学思路,深化问题思考,促使学生在丰富的生成中完善知识结构。
以苏教版数学四年级下册《用字母表示数》一课为例。在学习用字母表示数量关系的环节时,为了帮助学生学会数学化的表达,教师提供了一条信息:“小红今年5岁,妈妈今年30岁”,然后提问:“如果用a表示其中一个人的年龄,怎样表示另一个人的年龄?学生面对开放的问题,思维火花不断迸发:(a,b)、(a,a+25)、(a-25,a)、(a,a×6)。面对学生的动态生成,此时教师的引领对帮助学生学会正确地表示数量关系显得尤为重要,“你喜欢哪一种表示方法?为什么没有人选(a,b)?对于很多人选(a,a×6),你有什么话说?为什么女儿的年龄可以是a,又可以是a-25?a可以是任意自然数吗?”教师设计的这一系列问题,促进学生对用字母表示数量关系的反思并进行自主优化,帮助学生积累了符号化的数学活动经验。
二、还学生舞台
“和谐课堂”要求教师让出讲台,为学生提供一个表演、表达和表现的虚拟舞台,这个舞台有独角戏但更多需要的是“群戏”,学生都是舞台的明星,他们通过舞台研学,彰显个性,相互启发,辨别真伪,智慧碰撞,学会交流,学会欣赏,在多元互动中不断将思维引向深入,走向深刻,使自己真正成为学习的主人。
(一)把课堂讲解还给学生
学生的声音永远是“和谐课堂”的好声音,课堂讲解是一个将知识内化的过程,把知识的讲解权还给学生不仅可以调动学生学习的主动性,培养学生的表达能力,而且可以看出学生理解数学知识的差异,这种差异正是“和谐课堂”的动力和源泉,教师围绕学生之间的差异对不同的学生进行有针对性的点拨和引导,让不同的学生在“和谐课堂”的舞台上获得不同的提升。
在苏教版数学六年级下册《平面图形面积计算的总复习》教学中,教师安排学生自主整理平面图形面积计算的知识,然后在学习小组交流整理的成果,最后推荐小组代表在全班交流。发言学生指着自己的图或表进行讲解,汇报各种平面图形的计算方法和字母公式,并通过“我想提醒同学的是……”唤醒其他学生重新审视学习的难点。客观地说,这样的整理表现和学生的年龄特点与认知水平是相对应的。为了引导学生更深入地思考和建构,教师点拨学生继续围绕“我们还可以复习什么?面积公式之间有联系吗?你能用线将有关联的图形连一连吗?”进行交流,由浅入深地促进学生进入深层次的知识建构。
(二)把课堂展示让给学生
传统数学课堂上,教师展示的往往是教师需要的、有利于突破教学障碍的学习成果,对富有学生个性、思路另辟蹊径的数学思维,由于害怕“节外生枝”,教师多采取忽略的教学行为。“和谐课堂”就是要营造自然生长的生态环境,为学生提供施展才华的空间,呈现思维的典型性、独特性、开放性,表现百花齐放的勃勃生机。
在苏教版六年级下册《平面图形面积计算的总复习》中,教师坚持“和谐课堂”的理念,在练习的环节,让学生展示自己的“练习设计”——讲解自己的易错题。错误是学生造成的,学生对自己的错误最有发言权,展示错题的时候,就是学生暴露思维、反思、自我否定的时候。课堂展示还需要其他学生的互动交流,从独角戏演变成“群戏”,同学间精彩的互动会让他们从明白一道题的错误,到明晰一类题的错误,从而放大错误的资源,举一反三,既见树木又见森林,最终在错误中孕育成功。
(三)把课堂思辨留给学生
“和谐课堂”培养的学生往往“好为人师”,不甘心只当听众,他们乐于思考、勇于质疑、敢于思辨,善于通过辨析完善认知结构。
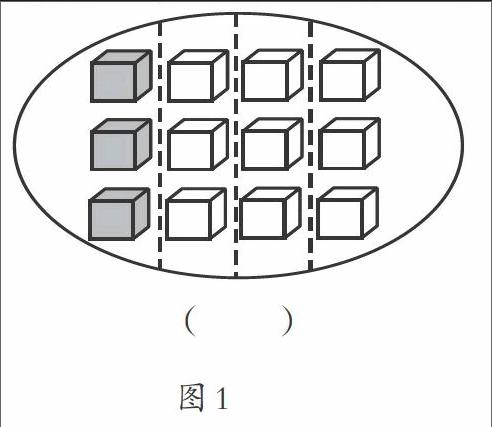
苏教版数学三年级下册《认识分数》第一课时“想想做做”第2题,如下所示,是一道用分数表示涂色部分的问题。
学生汇报时,出现了1/4、3/12、3/4三种答案。教师没有急于帮助学生弄清分母和分子的意义,而是先让答案是3/12的学生说出自己的想法,其次让那些急不可耐、支持1/4的学生说出反对意见,从而明晰了正确的方法,即先看这个整体被平均分成了几份,再看涂色的物体有这样的几份,最后再请那些写3/4的学生,允许他们重新选择答案,并说说当时的思考和现在的想法,学生在有序的思辨中加深了对“分数”与“份数”的沟通与联系的理解。
三、点学生所惑
在“和谐课堂”上,教师要有意识地隐匿自己的光芒,教师的“教”要像高手论剑一样,不轻易出手,只有在学生思维短路时巧妙点醒、在方法多样时精妙点拨、在经验建构时奇妙点化,学生才能在自主、开放、宽松的环境中释放个性,数学思维才能在主动发展中顿悟,教师的教才能避免越俎代庖。
(一)在学生思维短路时点醒学生
“和谐课堂”拒绝“灌输”,但不反对有针对性的“点醒”,当学生在数学活动中偏离、困顿、无法深入,同伴互助又无效时,教师可策略性地介入,及时进行学法指导。“点醒”不是和盘托出,而是凝练简洁地暗示思维的线索,用问题触发思考,让学生从紊乱的思维中醒来,找到思维行进的方向。
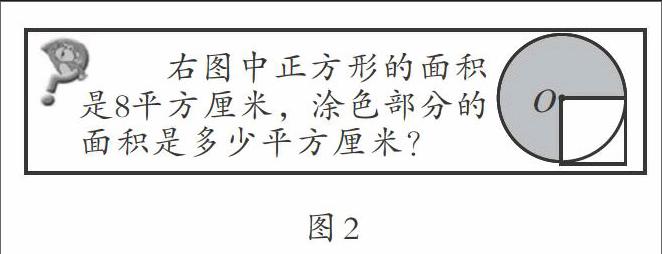
以苏教版五年级下册《圆的面积》教材第108页的思考题为例,如图2。
学生在解答时,或认为缺少条件不好解,或用8÷4=2(cm),以为2cm就是圆的半径。通过对学生的学情分析,教师会发现学生根据以往的解题经验,认为半径是求圆的面积的唯一条件,因此陷入思维的困顿,停滞在思维的误区。这时教师可以轻轻地叩问:“根据半径可以求圆的面积,但半径是求圆面积的唯一条件吗?想想圆的面积和小正方形的面积之间有什么直接的关系?”此时教师的点醒就像黑暗中划过的一颗流星,瞬间照亮了学生思维的荒野。学生恍然大悟后,教师追问:“以后求圆的面积,你认为需要什么条件,为什么?”教师在“和谐课堂”上介入性地“点醒”,对帮助学生驱走思维的障碍,挣脱思维的束缚,开阔认知的视野,起到了不可或缺的作用。
(二)在方法多样时点拨学生
数学“和谐课堂”突出培养学生思维的多样性和灵活性,在追求方法多样化的背后,“和谐课堂”更致力于培养学生根据不同的问题情境选择合适的方法,当学生下意识地进行方法的优化,但说不清为什么这样做的时候,教师的点拨犹如思维的催化剂,为每一个思考的心灵拨亮心灯。
在苏教版数学三年级下册《平均数》的学习中,学生掌握了求平均数的方法:移多补少与求和平分。為了帮助学生积累在问题情境中选择合适方法的经验,教师对教材“想想做做”的第1题进行了改进。先出示3个笔筒,要求学生求平均数的同时,比一比谁的反应快,学生通过观察发现3个笔筒里的铅笔数量都不多,不约而同地选择了移多补少的方法。然后教师增加了2个笔筒,仍然要求学生尽快求出平均数,此时5个笔筒里面的铅笔数量相差很大,学生在观察了一段时间后,放弃了移多补少的方法,选择了用求和平分的计算方法。“为什么求5个笔筒铅笔的平均数换了一种方法?你认为什么情况下用哪种方法更合适?”通过教师巧妙的点拨,引导学生静心思考两种方法对应的问题特征,使学生不仅知其然,而且知其所以然,提高了思维的深刻性。
(三)在学生进行认知建构时点化
小学生的年龄特点和认识水平往往束缚了他们向知识的核心内涵发展,容易对新知一知半解,或认识了表象,却无法接近本质。“和谐课堂”需要教师点化学生进行知识建构,引导学生把零散的认知穿成线、结成网,建立起牢固的知识结构,帮助学生既要看到知识的枝叶,又要看到知识的脉络和根须。
在苏教版数学二年级下册《倍的认识》的学习中,教师设计了认识“倍”、理解“倍”、抽象“倍”、设计“倍”四个活动来进行教学。在认识“倍”的数学活动中,学生借助图示对“倍”的概念进行了初步的表征,但对“倍”的认知建构缺乏自觉,理解的角度比较局限,漂浮在认知的浅层。因此在理解“倍”的数学活动中,教师可以增设题组练习,让“倍”动起来,在变化中引导学生进行观察思考:“2朵蓝花没变,为什么黄花朵数是它的2倍,而红花朵数是它的4倍?”“如果增加2朵蓝花,黄花朵数和蓝花朵数的倍数关系变了吗?为什么?红花朵数现在又是蓝花的几倍?”这样的问题点化就像一盏明灯,完善了“倍”的认知结构,在“倍”的学习中起到了画龙点睛的效果。
总之,在“和谐课堂”上教师要解放学生的双手和大脑,把认知和思想的主动权还给学生,贴近学生设计数学活动,促进学生成为问题的发现者、问题的提出者、问题的探究者,放手让学生去研究、去展示、去交流,改变什么都要教,什么都能教的教学习惯,在动态的生成中审时度势相时引导,让学生的激情在“和谐课堂”上飞扬,让学生在“和谐课堂”上幸福生长,提升学生的数学素养。
(责编 刘小瑗)
