初中数学符号语言的教学策略

蓝源添

【摘要】本文论述了初中数学符号语言的教学应结合初中生的思维特点，引导学生在理解数学符号的基础上展开记忆，渗透符号化思想，促使学生在应用数学符号的过程中形成符号意识，养成规范、准确运用数学符号的良好习惯。

【关键词】初中数学 数学符号 教学策略

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2017）02A-0078-02

众所周知，数学符号是数学学科经过不断传承与发展而形成的专用语言，在世界范围内通用。初中阶段是学生使用数学符号的重要时期，但是，由于多方面的原因，当前初中生对数学符号的掌握和应用现状存在着一些问题，主要表现为学生数学符号意识不强、符号记忆不够清晰准确、书写不够规范、没有养成使用数学符号的良好习惯等。为了让学生更加高效地学习数学，准确地掌握数学符号语言，并可以灵活地应用，教师可以采用以下四种策略展开教学。

一、诠释符号蕴含意义，帮助学生理解记忆符号

纵观当前初中阶段的数学符号语言学习活动，很多教师都是采取简单直接的方式展开教学，让学生机械地记忆数学符号。由于学生只能孤立地记忆数学符号的形状，不能建立各种数学符号之间的联系，所以大脑中存储的符号信息也比较单薄。教师应结合不同的数学符号，挖掘符号所代表的意义，诠释数学符号蕴涵的价值，帮助学生理解记忆，提升数学符号记忆的效果。

例如，在教学人教版数学七年级上册《有理数的乘方》一课时，内容涉及an这个用来表示“乘方”运算的符号，以及由这个符号衍生出来的a2、b2、a3、b3等相关的数学符号。对于这些符号，学生只有清晰地理解符号代表的意思，才能准确地书写，正确地解答数学题目。因此，笔者在教学时特别强调了对a2+b2、（a+b）2、a+b2、a3+b3、（a+b）3等一些常见的算式符号的意思，让学生展开比较记忆，进一步培养学生思维的条理性。笔者先让学生结合已经学习的知识，尝试着逐一阐述各个算式的意思：a2+b2表示甲乙两个数的平方和；（a+b）2表示甲乙两个数和的平方；a+b2表示甲数与乙数平方的和；a3+b3表示甲乙两个数的立方和；（a+b）3表示甲乙两个数和的立方。最后让学生进行对比，区别不同，加强学生对这些基本算式所表示的意思的理解，有效地帮助学生避免混淆这些数学符号，让学生在今后的数学学习中正确使用。

理解记忆已经逐渐成为初中生记忆知识要点的主要方式。教师通过构建数学符号的意义体系，增强学生对数学符号相关信息的感知，让学生在理解符号意义的基础上进行识记，促使学生记得更加牢固。

二、讲述历史知识，引导学生学习内化符号

初中生的思维逐渐由形象思维向抽象思维转变，对事物的认知也更加倾向于抽象的理性认识，对事物所形成的知觉也更加准确和快速，尤其是在观察事物细节方面的能力有很大的提升，更擅长对事物细微差别的认识与把握。学生的这些认知能力的提升无疑对数学符号的学习是有帮助的。教师应结合初中生的能力结构和水平，通过讲述一些数学符号的历史，引导学生在记忆的基础上快速内化并掌握数学符号。

例如，在教学八年级上册《平方根》一课时，教材引入了“平方根号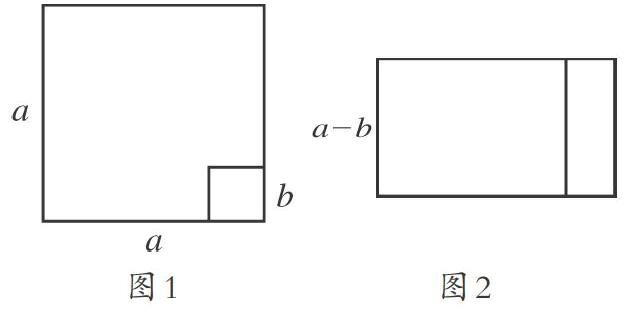”这一非常重要的数学符号，由于学生小学阶段没有接触过有关根号的信息，无法产生联想记忆，为了帮助学生准确地记忆和应用这一符号，教师对平方根号的由来进行了简要说明：“在英语中，‘根的单词是‘radix，而这个单词追根溯源来自于拉丁文中的单词‘Radix。开始人们用R和X两个字母表示平方根号，但是比较复杂，在17世纪初期，数学家笛卡尔在编写《几何学》一书时，率先使用了‘√来表示‘二次根号。大家仔细观察，笛卡尔当时用的这个符号与字母r比较像，也就是说二次根号的符号是由字母r变形得到的，后来因为需要表示‘开平方的范围，所以在‘√的基础上又增添了上面的‘-，从而变成了现在我们看到的‘的形式。”学生在听完笔者的介绍后，对平方根号的发展演变获得了一定的认识和了解，大脑中丰富了平方根号的信息，进而内化并吸收了这个符号。

三、创设解决问题情境，促使学生练习应用符号

应用数学符号解决实际问题既是学习掌握这种数学语言的最终目标，也是强化学生数学符号学习效果的有效途径。教师应结合学生所学习的数学符号，运用恰当的方式为学生创设解决问题的情境，为学生提供应用数学符号的机会，让学生可以自由地选用数学符号，准确地应用符号来解决问题。在这种真实的应用实践中，通过有效地练习应用符号，达到掌握数学符号的最终目标。

例如，在教学八年级数学下册《平行四边形》一课后，为了增强学生数学符号的应用意识，笔者创设了一个解决问题的学习情境：“平行四边形的底比高多10厘米，在这个平行四边形上剪掉一个以平行四边形的高为边长的正方形，求剩余部分的面積是多少？”对这种问题，学生首先想到了平行四边形的面积计算公式S=a×ht和正方形的面积计算公式S=a×a。接着，笔者让学生根据题意“平行四边形的底a比高h多了10厘米，即a-h=10cm”，那么，平行四边行的面积减去边长为h的正方形的面积，可以列出算式是S=a×h-h×h，然后把h=（a-10）代入，化简后得到S=10a-100。学生在解答这个题目的过程中，自觉地运用了数学算式、数学符号，强化了对数学符号的记忆。在这样的解题活动中，学生的数学符号意识得到了有效加强，学生应用数学符号解决实际问题的能力也得到了有效锻炼。

学以致用可以强化学生对数学符号的认知，也能够让学生真正体验掌握数学符号的意义和价值，从而产生强烈的学习数学符号的动机。教师通过为学生创造机会，加强数学符号的应用练习，提高了学生掌握数学符号的效果。

四、解析数学思想方法，增强学生认识理解符号

数学符号是数学语言的重要组成部分，而数学语言是数学思想方法的集中体现。教师通过为学生分析数学符号所包含的数学思想方法，以数学符号为载体和途径，成功地向学生渗透数学思想，能够促使学生数学思维的形成，指导自己的数学学习行为，也可以增强学生认识数学符号、拓展数学符号，让学生能更加准确地应用数学符号。

例如，数学符号中有用字母来表示数字、用字母与几何图形一起来表示几何图形等，这些数学符号简练地反映出了数字与数字、数字与算式等各种数学关系，体现了数学中最基本的“数形结合”的数学思想。笔者在引导学生学习数学符号的同时，也以数学符号为载体，对学生进行数形结合思想方法的渗透。“结合我们学过的数学知识，在图形的帮助下，尝试推导平方差公式，即a2-a2=（a+b）×（a-b）。”笔者设计学习任务，并且画出了下面两个图形给学生提示。

学生根据笔者的提示，运用正方形、长方形的面积公式，结合图形顺利地推导出了a2-b2=（a+b）（a-b）。在这个过程中，学生不仅运用了数学符号、图形符号，还亲身体验了数形结合的思想方法，从而加深了对数学符号的理解。

掌握数学符号，学好数学语言，不但是学好数学的必然要求，也是训练学生数学思维、培养数学学习能力的重要手段。教师要积极探寻数学符号教学的有效手段，避免简单机械的记忆，帮助学生正确地读写、规范地使用数学符号，开启数学学习的大门，引领学生真正走进神奇的数学天地。

（责编 林 剑）