一种优化的AES算法及其FPGA实现*

张 伟 高俊雄 王耘波 武文斌

(华中科技大学光学与电子信息学院 武汉 430074)

一种优化的AES算法及其FPGA实现*

张 伟 高俊雄 王耘波 武文斌

(华中科技大学光学与电子信息学院 武汉 430074)

针对AES算法加密解密结构的不一致提出了一种优化算法,得到了统一的加密解密流程,有效节省了资源消耗。为取得速度和资源的折中,AES加密解密主体采用内外混合流水线结构,其中S-box和逆S-box采用基于正规基的有限域算法实现。基于对各电路模块路径延时的分析,对AES轮变换进行了6级流水线划分。在Xilinx公司XC7VX485T FPGA上综合结果显示:电路资源消耗为19006LUTs,最高工作频率为724.323MHz,数据吞吐量为92.713Gbps,获得了非常好的加速效果且有效降低了资源消耗。

AES算法; 全流水线; FPGA

Class Number TP309.7

1 引言

计算机、网络与通信技术的飞速发展,各类敏感数据通过开放网络进行传输带来了严峻的信息安全问题,一个有效的解决办法就是使用分组密码算法。其中,高级加密标准(Advanced Encryption Standard,AES)算法[1]以其安全、简洁和高效等优点广泛应用在智能卡、移动电话和电子金融等各种应用中。

AES硬件实现相比软件实现提供了更好的物理安全性及更快的处理速度,FPGA以其可编程性成为了AES算法的理想实现平台。随着业界不断提高的计算性能需求,提升AES电路吞吐量相比于减小资源消耗、降低功耗等目标得到了更大的关注。Zhang[2]、Hodjat[3]、Zambreno[4]等采用全流水线结构大大提高了AES电路的吞吐量。

本文在分析AES算法结构的基础上提出了一种加密解密流程一致的优化AES算法,有效减小了资源消耗。安全性分析及密码学测试表明该优化方案不会减弱密码安全强度。采用全流水线结构在FPGA平台上实现优化算法,达到了速度与资源的平衡。

2 AES算法及优化

2.1 算法简介

AES是一种迭代分组密码算法,加解密主体采用代替/置换网络(Substitution/Permutation Net,SPN)结构,算法流程如图1所示。AES加密算法中分组长度固定为128bits,密钥长度可选择为128bits、196bits或256bits,对应的轮变换次数Nr分别为10、12和14,本文密钥长度选择为256bits。AES加密算法轮函数由四层变换组成:字节替换是对状态矩阵中每一字节的非线性替换;行移位变换将状态矩阵中每一行分别循环左移0、1、2和3个字节;列混合变换将状态矩阵每一列看作系数取自GF(28)次数小于4的多项式,将其与一个固定多项式c(x)={03}x3+{01}x2+{01}x+{02}相乘后模x4+1;轮密钥加变换将轮密钥异或到状态矩阵中每个字节。AES解密算法通过逆序使用加密算法中各变换的逆变换,将密文转换为明文,其中轮密钥加变换中各轮密钥的使用顺序与加密流程相反。对于AES算法中各变换详细操作可参考文献[1],不再赘述。

2.2 算法优化

AES算法中加密解密流程是不同的,在同时实现加密和解密功能的电路中解密流程一般采用等效解密算法结构,通过共用部分资源以减小电路面积。AES电路轮变换结构如图2所示。上面的数据通路实现加密功能;下面的数据通路实现解密功能。然而,每一时刻电路只能实现加密或解密一种功能,部分功能模块将不会起作用,造成了资源的浪费。虽然可以采用在字节替换与逆字节替换中共用乘法逆变换,将逆列混合变换矩阵分解为列混合矩阵与常数矩阵的乘积等方式实现部分电路的共用,电路中还是有部分资源浪费。

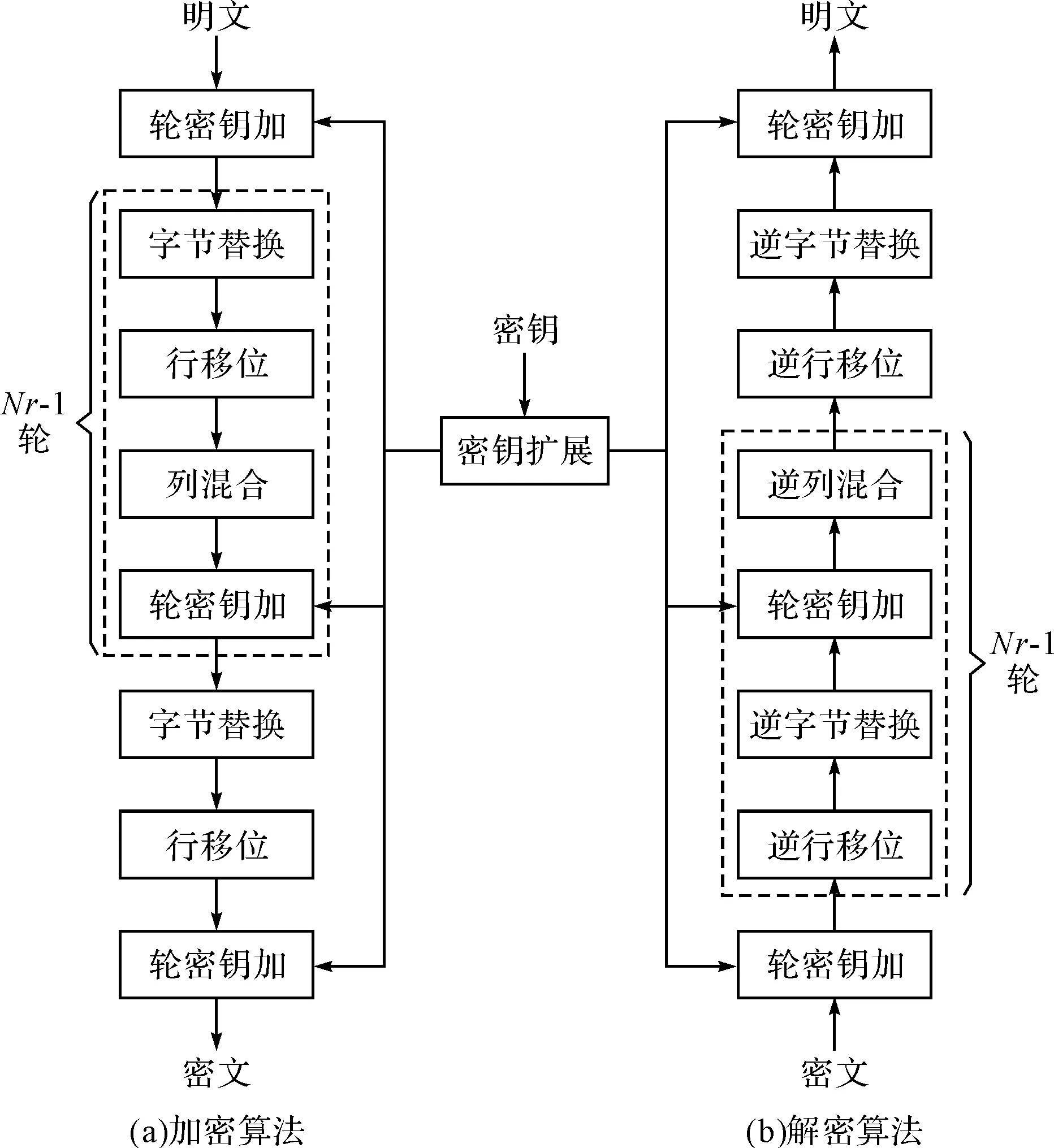
图1 AES加解密流程

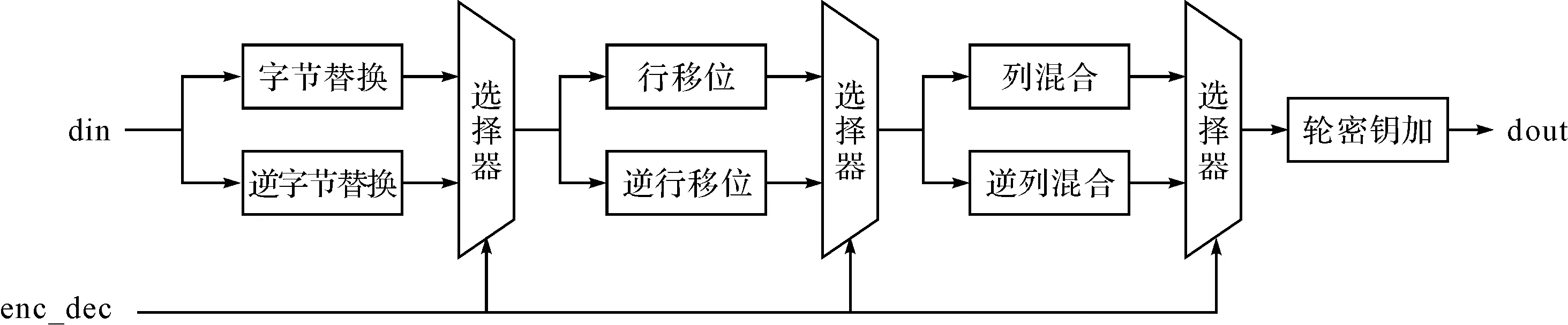
图2 AES加解密轮变换结构图

文献[5]提出将列混合中固定多项式c(x)变为正交矩阵使得逆列混合变换与列混合变换相同,即d(x)=c-1(x)。这种优化方案可以减小资源消耗,并且路径延时也会降低。令c(x)=c3x3+c2x2+c1x+c0,由c(x)·c(x)=E(E为单位矩阵)可得到c1=c3且c0+c2={01}。本文改进方案中选择c(x)={01}x3+{02}x2+{01}x+{03},选择较小的系数有利于减小硬件资源消耗。

将14次轮变换分为奇数轮和偶数轮交替进行,在奇数轮和偶数轮中分别使用原AES算法中加密轮变换和等效解密轮变换,即奇数轮由字节替换、行移位、列混合和轮密钥加组成,偶数轮由逆字节替换、逆行移位、列混合(本文改进方案中列混合变换的逆变换为列混合本身)和轮密钥加,优化后AES加密解密流程如图3所示。由于奇数轮变换和偶数轮变换互逆,改进算法解密流程与加密流程完全相同。与原AES算法一样,解密算法需要将中间13个轮密钥进行一次列混合变换以得到等效的解密子密钥。

图3 优化算法加解密流程

2.3 优化算法安全性分析与测试

AES算法中S-box的密码性质决定了算法的安全性。文献[6]分析了S-box和逆S-box的密码学性质,可以看出S-box和逆S-box差分均匀度、非线性度等完全一致,差别在于S-box比逆S-box严格雪崩准则距离小但代数式项数也较小,所以S-box扩散性能比逆S-box要好但代数结构复杂度要低。本文交替使用S-box和逆S-box可以充分利用两种置换表的优点。

行移位和逆行移位都是将状态矩阵每一列中4个字节移动到不同列中,只是字节移位的方向不同,两种变换的扩散性能完全一样。文献[7]证明了当c(x)是GF(28)中不可约多项式时,改变c(x)不会降低算法抵抗截断差分分析和差分分析的能力;文献[8]证明了本文选择的c(x)与原AES算法中列混合系数都具有最大分支数5,故本文优化方案不会影响列混合变换的扩散效率。

分组密码算法本身应是一个好的伪随机数发生器。目前分组密码的统计测试通常关注密文随机性、明密文独立性和明文扩散性等,具体测试方法可参考文献[9]。对原AES算法及改进AES算法进行统计性测试,分组长度和密钥长度分别为128bits和256bits,显著性水平为0.05,测试次数为120次,统计结果表明原AES算法和优化AES算法都能够很好地隐蔽输入明文的数据特征,使密文表现出良好的随机性,优化算法安全性并未减弱。

3 优化算法FPGA实现

本文设计电路整体结构如图4所示。

图4 AES加密解密电路结构图

KeyExpansion模块将输入的256bits初始密钥扩展生成各轮变换所需轮密钥。KeyBuffer为15个128bits寄存器组,用于存储轮密钥。Encryption/Decryption是加密/解密主体部分,包含上文所述的各变换。字节替换/逆字节替换、列混合电路是高性能AES硬件电路实现的关键,将在下文进行详细介绍。

表1为图4中各信号定义及功能说明。

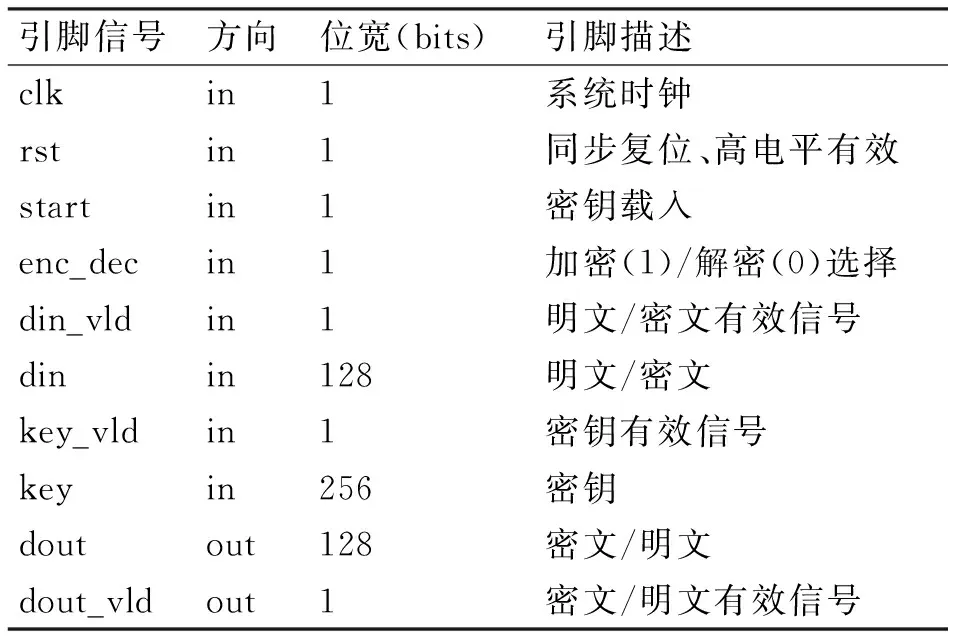
表1 接口声明

3.1 S-box/逆S-box

基于查找表的S-box/逆S-box方案可以避开繁杂的数学公式推导和内部逻辑优化,然而此方案缺点也很明显:加密和解密需要两个不同查找表使得电路资源消耗较大;固定的电路路径延时限制了频率提高,因此在高速应用中较少采用基于查找表结构的S-box。

文献[10]最先提出基于复合域分解的可复用S-box方案使得电路易于进行流水线处理提高吞吐量。文献[2]采用基于多项式基的复合域GF((24)2)运算实现了最快速的S-box。文献[11]采用基于正规基的复合域算法得到了最紧凑的S-box电路。本文采用文献[11]中S-box实现方案以减小资源消耗,图5所示为奇数轮中S-box结构图,S-box与逆S-box各部分电路资源消耗和路径延时如表2所示。

图5 奇数轮S-box电路结构

表2 S-box与逆S-box资源消耗和路径

3.2 列混合电路

优化算法选择c(x)={01}x3+{02}x2+{01}x+{03}作为固定多项式来统一实现列混合和逆列混合,相应矩阵形式为

(1)

式(2)为{02}x计算结果,资源消耗和路径延时分别为3XOR和1XOR,带入式(1)可得列混合电路资源消耗和路径延时分别为86XOR和3XOR,其中s0,c+s2,c、s1,c+s3,c、{02}(s0,c+s2,c)和{02}(s1,c+s3,c)为公共项。{02}x={02}·{x7,x6,x5,x4,x3,x2,x1,x0}

={x6,x5,x4,x3⊕x7,x2⊕x7,x1,x0⊕x7,x7}

(2)

3.3 轮单元流水线划分

根据上述对S-box、逆S-box、列混合电路的设计,考虑到各模块的路径延时,对AES算法中轮变换进行6级流水线划分,图6为奇数轮变换示意图。

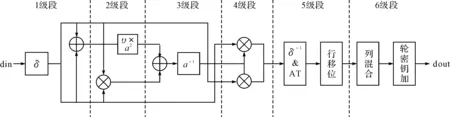
图6 奇数轮流水线

由各模块路径延时可得出流水线关键路径出现在第2级和第4级,路径延时为5XOR+1AND,最小路径延时为第5级的3XOR,显然路径延时不够均匀。

图7 GF(24)乘法器

图7为GF(24)中乘法器电路,根据路径延时将乘法器分为了三部分:第1部分计算乘数和被乘数各自高低2位的异或,路径延时为1XOR;第2部分路径延时为GF(22)中乘法器延时(2XOR+1AND)加上N×c模块路径延时(1XOR)的和,即3XOR+1AND;第3部分为N×c模块输出与第2部分中上下2个乘法器输出的异或,路径延时为1XOR。为平衡流水线各级路径延时,实现第2级中乘法器时将乘法器中第1部分移动到流水线第1级,实现第4级中2个乘法器时将乘法器第3部分移动到流水线第5级。通过对GF(24)中乘法器的分解,可将流水线关键路径减小为4XOR+1AND,提高了系统时钟频率。本设计中最终流水线结构各分段延时如表3所示。

表3 AES-256轮单元流水线各级路径时延

4 仿真与综合

加密算法仿真结果如图8所示,输入初始明文为128′h00112233445566778899aabbccddeef0,此后每一时钟周期明文加1;密钥为256′h603deb101

5ca71be2b73aef0857d77811f352c073b6108d72d981

0a30914dff4,输出初始密文为128′h82ac6b0710da9

87ad96d8867c2141f56。采用同样的密钥,将加密输出密文进行解密可得输出明文为128′h00112233

445566778899aabbccddeef0等,经验证加解密功能完全正确。

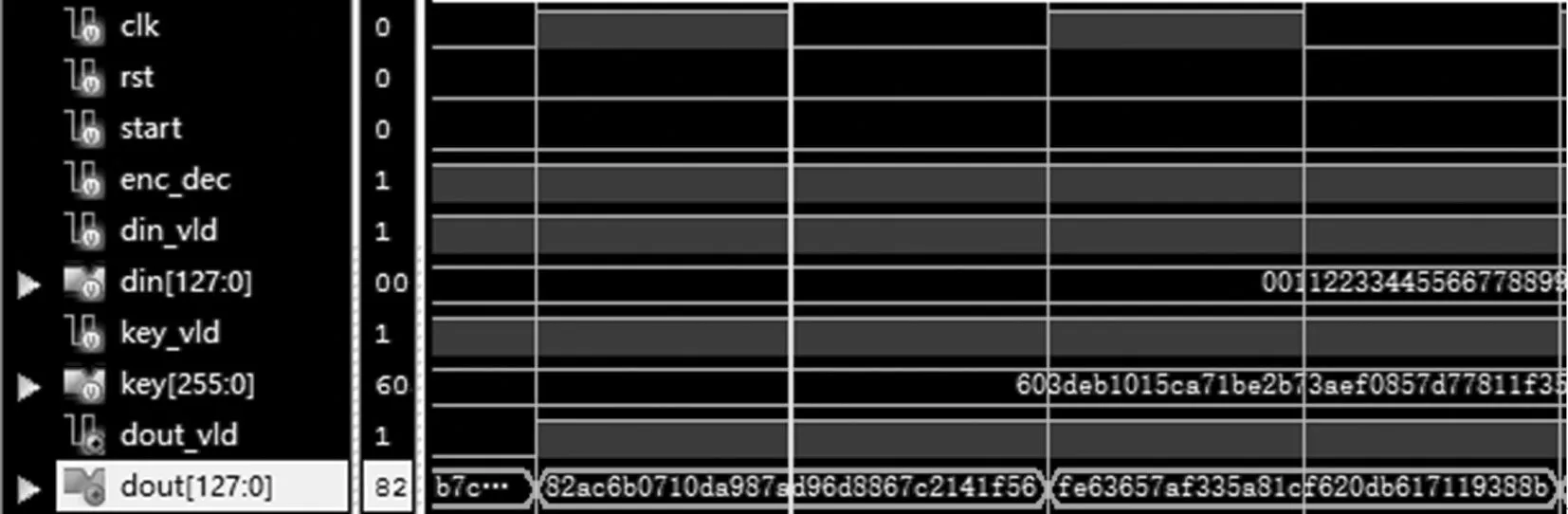
图8 加密功能仿真

选择Xilinx公司的XC7VX485T,使用ISE综合显示资源消耗为19006LUTs,最高工作频率为724.323MHz,计算得到数据吞吐量为92.713Gbps,获得了非常好的加速效果且有效降低了资源消耗。

5 结语

AES算法以其安全、高效得到了广泛的应用。本文针对AES算法加解密流程不一致提出了一种优化方案以减小资源消耗。在FPGA实现中,采用基于正规基的复合域算法实现S-box和逆S-box有效缩减了资源消耗。通过分析电路各模块路径延时进行了轮单元的6级流水线划分,实现了工作频率和吞吐量的提升。最终实现结果表明本设计达到了资源与速度的有效折中,实现了高性能的AES加解密电路。

[1] Dobbertin H, Knudsen L, Robshaw M, et al. Advanced Encryption Standard — AES[J]. Lecture Notes in Computer Science,2005,3373(8):2200-2203.

[2] Zhang X, Parhi K K. High-speed VLSI architectures for the AES algorithm[J]. IEEE Transactions on Very Large Scale Integration Systems,2004,12(9):957-967.

[3] Hodjat, A, Verbauwhede, I. A 21.54 Gbits/s fully pipelined AES processor on FPGA[M]. IEEE,2004:308-309.

[4] Zambreno J, Nguyen D, Choudhary A. Exploring Area/Delay Tradeoffs in an AES FPGA Implementation[M]. Heidelberg: Springer Berlin Heidelberg,2004:575-585.

[5] Jing M H, Chen J H, Chen Z H. Diversified Mixcolumn transformation of AES[C]//International Conference on Information, Communications & Signal Processing,2008:1-3.

[6] 张丽红,凌朝东.基于AES算法中S盒的分析研究与改进[J].信号处理,2011,27(9):1428-1433. ZHANG Lihong, LING Chaodong. The analysis and improvement of S box based on AES[J]. Signal Processing,2011,27(9):1428-1433.

[7] 冯国柱,李超,多磊,等.变型的Rijndael及其差分和统计特性[J].电子学报,2002,30(10):1544-1546. FENG Guozhu, LI Chao, DUO Lei, et al. Transmutative Rijndael with the Differential and Statistical Charactartics[J]. Acta Electronica Sinica,2002,30(10):1544-1546.

[8] 李京,李永珍.AES改进算法在CCMP协议中的应用[J].延边大学学报:自然科学版,2015(3):244-248. LI Jing, LI Yongzhen. Improvement of the AES encryption algorithm and its application in CCMP protocol[J]. Journal of Yanbian University(Nature Science Edition),2015(3):244-248.

[9] 冯登国.分组密码的设计与分析[M].北京:清华大学出版社,2000:407-415. FENG Dengguo. Design and analysis of block cipher[M]. Beijing: Tsinghua university press,2000:407-415.[10] Wolkerstorfer J, Oswald E, Lamberger M. An ASIC Implementation of the AES SBoxes[C]//Topics in Cryptology-CT-RSA 2002, The Cryptographer’s Track at the RSA Conference, 2002, San Jose, CA, USA, February 18-22, 2002, Proceedings,2002:67-78.

[11] 曾纯,吴宁,张肖强,等.基于多因子CSE算法的AES S-盒电路优化设计[J].电子学报,2014(6):1238-1243. ZENG Chun, WU Ning, ZHANG Xiaoqiang, et al. The Optimization Circuit Design of AES S-Box Basedon a Multiple-Term Common Subexpression Elimination Algorithm[J]. Acta Electronica Sinica,2014(6):1238-1243.

An Optimized AES Algorithm and Its FPGA Implementation

ZHANG Wei GAO Junxiong WANG Yunbo WU Wenbin

(School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074)

For the encryption and decryption structure of AES is not consistent,an optimized AES algorithm with a unified encryption and decryption process is proposed in this paper. Using the fully pipelined architecture, the proposed circuit achieves an effective tradeoff between speed and resources, among which the S-box and inverse S-box are implemented applying the finite field algorithm based on regular basis. With the analysis of the path delay of each module, the AES round transformation is divided into 6 stages. Results implemented in the Xilinx’s XC7VX485T FPGA show that the hardware resource consumption is 19006LUTs,the maximum frequency is 724.323MHz and the throughput can get to 92.713Gbps, thus obtaining a very good acceleration effect.

AES, full pipelining, FPGA

2016年9月7日,

2016年10月20日

张伟,男,硕士研究生,研究方向:加密算法。高俊雄,男,博士,讲师,研究方向:虹膜识别。王耘波,男,博士,副教授,硕士生导师,研究方向:人工智能与系统集成。武文斌,男,硕士研究生,研究方向:人脸识别。

TP309.7

10.3969/j.issn.1672-9722.2017.03.020