基于DS证据理论的粉尘浓度数据融合算法研究*

景 航 于小宁

(西安工业大学电子信息工程学院 西安 710021)

基于DS证据理论的粉尘浓度数据融合算法研究*

景 航 于小宁

(西安工业大学电子信息工程学院 西安 710021)

针对采用DS证据理论处理粉尘浓度数据时,不能有效处理冲突问题,结合粉尘检测原理,分析了粉尘颗粒在空间中的受力情况,粉尘颗粒在空间中的运动状态分析了粉尘颗粒的扩散,获得粉尘浓度分布,依据粉尘浓度分布特点,提出适用于粉尘浓度数据的一种概率赋值函数获取方法,并提出一种新的融合规则消除冲突。

DS证据理论; 粉尘浓度; 冲突

Class Number TP391

1 引言

证据理论是一种不确定性推理方法,近年来有了很大发展,正受到越来越多的关注。D-S理论提供了一个有用的相关证据的合成方法,能够融合多个证据源提供的证据,从而成功地应用于数据融合与目标识别领域。但是,D-S理论的合成公式存在不足,特别是,证据之间存在冲突时,合成结果可能有悖常理。Yager[1]提出一种方法,把支持证据冲突的那部分概率全部赋给了未知领域,方式过于保守,在多个证据冲突时,结果也不理想。孙全[2]把支持证据冲突的那部分概率分配给各个命题,融合结果比较理想。本文针对浓度数据特点,提出了一种融合方法。多点检测粉尘浓度方式下,采用本方法进行数据融合,结果优于经典DS证据理论,尤其在数据高度冲突时,融合结果符合实际情况。

2 DS证据理论及其不足

2.1 DS证据理论

DS证据理论是一种不确定推理方法,最初在1967年由Dempster[3]创立,1976年,其学生Shafer针对统计问题给出了来自两个独立信息源的证据的合成法则,即Dempster合成法则[4]。DS证据理论可以清楚地表达不确定、不知道的信息,在无须任何先验信息的基础上有效地处理不确定信息,因此,被广泛应用于模式识别、不确定信息决策、目标识别等广大领域。

DS证据理论定义如下:

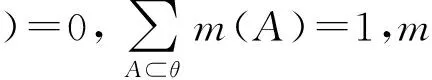
2) 在辨识框架θ=(φ1,φ2,φ3,…,φn)下,有两条证据F1,F2,m1和m2为其相对应的基本概率赋值函数,DS证据组合规则如下:

(1)

(2)

当K-1=0时,m1⊕m2无定义,m(A)不存在,即m1和m2高度冲突,因此,K的大小反映的是两条证据之间的冲突程度。

2.2 证据理论的不足

在证据冲突较小时,DS证据理论组合规则能够将证据置信度不断地向确定性较高的命题集中,但是在证据冲突较大或者完全对立时,由于DS证据理论将冲突全部丢弃[5],失去了其融合能力,合成结论往往有悖于实际情况[6]。下面举例说明。

有识别框架θ=(F1,F2,F3),有两条证据如下

m1(F1)=0.9,m1(F2)=0,m1(F3)=0.1
m2(F1)=0,m2(F2)=0.8,m2(F3)=0.2

根据DS证据理论融合结果如下:

K=0.02,m(F1)=0,m(F2)=0,m(F3)=1

显而易见这个融合结果不正确,证据对F1和F2高度支持,F3支持度低,但是融合结果却高度支持F3。因此,当证据高度冲突时,DS证据理论失效。

3 粉尘浓度检测原理及数据特点

3.1 粉尘检测原理

透射法的基本原理:当一束单色平行光垂直通过某一均匀非散射的待测物质时,由于颗粒的散射和吸收作用,出射光强会有一定程度的衰减[11],根据Lambert-Beer定律得:

I(λ)=I0(λ)exp[-α(λ)LC]

(3)

式中:λ为入射光的波长,I0(λ)和I(λ)分别为光线经过待测物质时的入射光强和出射光强,α(λ)为待测物质在波长λ处的吸收系数,C为待测物质的浓度,L为光束传播方向上待测物质的长度。因此可通过检测出射光强I(λ)获得待测物质的浓度C。

(4)

对于确定系统,-α(λ)L是一个定量,只要得出I与I0的比值即可求出浓度值C。粉尘检测原理图如图1所示,光源射出的光经过准直透镜变为平行光,由分光镜分成两束具有同一性的光,一束平行光经聚焦透镜汇聚到探测器1处,探测器1输出信号作为参考信号I0;另一束平行光通过粉尘检测区,经聚焦透镜汇聚到探测器2处,探测器2输出信号作为浓度信号I。

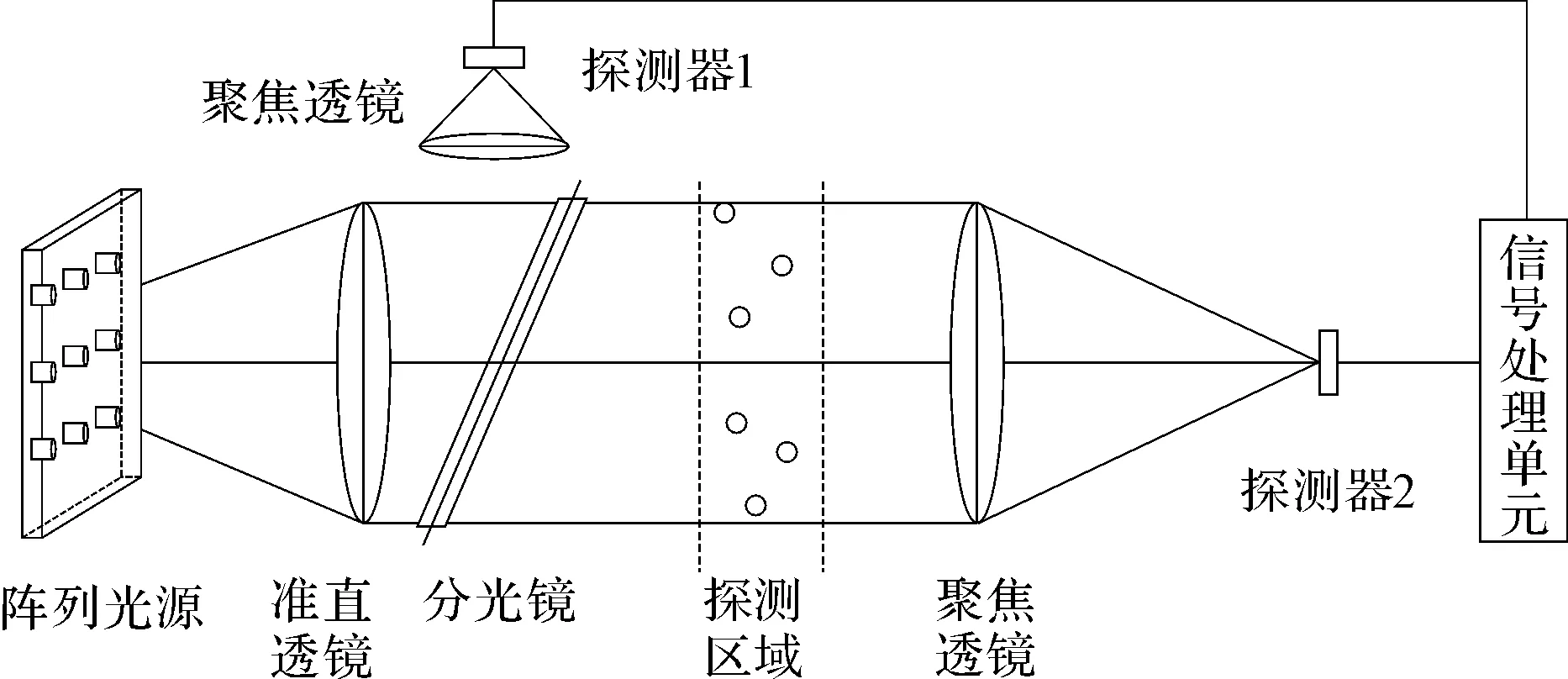
图1 粉尘检测原理图

3.2 粉尘浓度分布

由于单点测试不能全面、有效地检测被侧区域的浓度值,并且,单点测试容错率低,易受干扰,所以本文提出了多点检测。

3.2.1 粉尘颗粒的受力情况

粉尘颗粒由于受到空气流动中各个力的作用,如式(5)所示：

(5)

式中:m是尘粒的质量,kg;Vm代表尘粒的运动速度,m/s;t为尘粒的运动时间,s。fg为重力,ff为浮力,fd为气动阻力,fp是压强梯度力,fm、fa、fs、ft分别为附加质量力、巴塞特(Basset)力、萨夫曼(Saffman)升力以及马格努斯(Magnus)效应。

通过量阶分析可知,在粉尘浓度较低的情况下,阻力、重力、浮力为主要作用力,其它各力的量级很小,可忽略不计。尤其在稀相气固两相流中,粉尘颗粒的浓度较低,而且气体密度比尘粒密度小得多,约为10-3数量级,所以尘粒所占的体积比气体所占体积小得多,因此为简化尘粒的运动方程,忽略尘粒所占的体积。忽略力fa、fp、fs和ft的作用,只考虑重力fg浮力ff和阻力fd的作用,则球形尘粒的运动方程为

(6)

式中:ρm代表尘粒的密度,kg/m3；d表示尘粒的直径,m；Cm为阻力系数,表示阻力的性质和大小；g是重力加速度；Vg是气体的运动速度。

3.2.2 粉尘颗粒在空间中的运动状态

由于各个力的作用,颗粒在空间有一定的运动状态。

粉尘自身重力对粉尘在空间中运动影响较大,重力对粒子扩散的影响可使其扩散中心向下倾斜,在z向需用粒子沉降距离加以修正,以z+vt来代替。T是粉尘扩散至下风向x距离所用的时间,t=x/u;vt为粒子在大气中的沉降速度。

(7)

式中:ρm是粒子密度，ρg是空气密度，d是粒子半径，Cs是空气阻力系数。

针对尘粒与风流的相对运动状态,一般都在雷诺数Re≤1的范围,且ρg≤ρm,由stokes方程可得:

(8)

式中μ为空气粘性系数。

当不同直径的尘粒以一定的速度v0抛向空中,由于空气阻力的存在,尘粒的运动速度将减慢,最终在重力的作用下沉降。忽略运动过程中重力的作用,尘粒的初速度将克服摩擦而在气流中做克服摩擦减速运动,这样可以推导出粉尘的水平运动速度为

(9)

从0时刻到τ时刻的水平运动距离为

(10)

3.2.3 粉尘颗粒的扩散

由于气流的存在,粉尘颗粒在空间有扩散过程,实际情况中气流处在湍流,而在湍流状态下,使粉尘扩散过程十分复杂,很难用简单的方程式来描述,这里仅用有向单一方向均匀流动的湍流扩散过程进行讨论。

(11)

其中，Hx、Hy、Hz为扩散的三个方向的湍扩散系数。

给定边界条件:在原点x=y=z=0时,c→∞,在无限远处x,y,z→∞时c=O。同时假定扩散过程中粉尘质量守恒,在下风向任一yoz平面的粉尘总量等于源强J可以写出积分式：

式中u为气流速度。

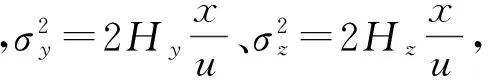
(12)

在实际环境中,粉尘颗粒处在大气环境中属于气固两相流体,由式(5)可知作用在粉尘颗粒上的作用力有多种,在这些力的作用下,粉尘颗粒在空间中有一定的运动状态,如式(7)、(9),这些运动状态在空间中形成了一定的扩散运动,使得粉尘浓度分布在一定区域内时均匀分布,各个位置的浓度值在理想条件下相等,以各个位置为横坐标,以浓度值为纵坐标,在理想状态下各点的浓度值成一条直线存在。但是,在实际中由于环境的因素和颗粒自身的差异性,各点的浓度值会在这条理想直线上下波动,在一定范围内成连续变化,如图2所示。

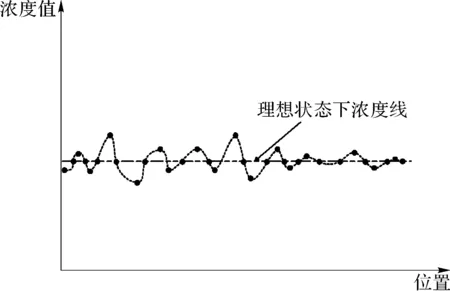
图2 浓度理想状态直线图

4 粉尘浓度数据融合

4.1 概率赋值函数的获取

DS证据理论的概率赋值函数不易获取,由第3节可知,粉尘浓度分布在一定空间内均匀分布,各浓度值在一定范围内连续变化,针对此特点,本文提出一种概率赋值函数获取方法。

1) 周期性同时采集多个浓度值。

2) 由于一定区域内的浓度值连续变化,且在一定范围内提取出最大值和最小值,把最大值和最小值之间的值域按周期数等分,得出几个区域,那么辨识框架θ内就有几个元素,也就有几个命题。

3) 统计各个检测点周期性得到的浓度值,把每个检测点测的浓度值按所划分区域分别落入对应的区域,统计每个检测点在每个区域内的个数,最后依次除以周期数,得到概率赋值函数。

4.2 改进的融合规则

辨识框架θ有n个元素,统计辨识框架θ内第一个元素中所包含的所有浓度值[10],并统计这些浓度值与其他元素中的浓度值的差值,分别记为D12,D13,D14,…,D1n。

以此类推分别统计每个元素中的浓度值与其他元素的浓度值的差值,得到矩阵A

(13)

这个矩阵是一个对称矩阵,对角线上的元素均为1。

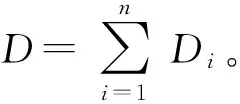
定义元素的信度为

(14)

即每一个元素与其他元素的浓度值之差越小,被证据的支持程度越高[7],信度越高。

构建新的组合规则

(15)

将冲突按元素B的信任度βi大小分配。

将结果中置信度最高的元素的浓度值进行统计,哪个浓度值的D最小,即此浓度值为融合结果[8]。

5 计算与分析

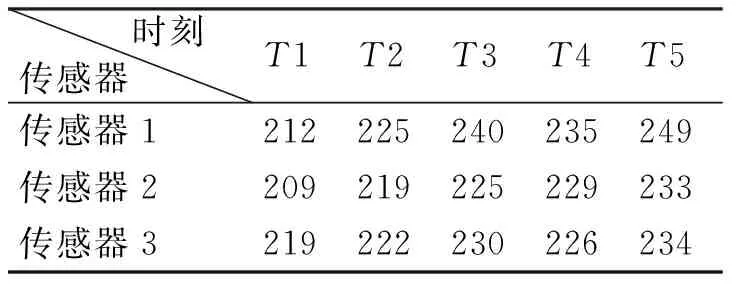
表1 3个不同位置的粉尘浓度值

表1是由三个不同位置的传感器在五个时刻同时采集到的大气粉尘浓度值[9],单位为μg/m3,三个证据源分别记作m1,m2,m3。采用本文所提方法获得的概率赋值函数,具体步骤如下:

1) 最大的浓度值为249,最小的浓度值为209,按周期数五等分,[209,217]、(217、225]、(225、233]、(233、241]、(241、249]。

即统计辨识框架θ有五个元素，分别记作B1、B2、B3、B4、B5,三条证据的概率赋值分别为

m1(B1)=0.2、m1(B2)=0.2、m1(B3)=0、
m1(B4)=0.4、m1(B5)=0.2
m2(B1)=0.2、m2(B2)=0.4、m3(B3)=0.4、
m2(B4)=0、m2(B5)=0
m3(B1)=0、m3(B2)=0.4、m3(B3)=0.4、
m3(B4)=0.2、m3(B5)=0

2) 获得A矩阵

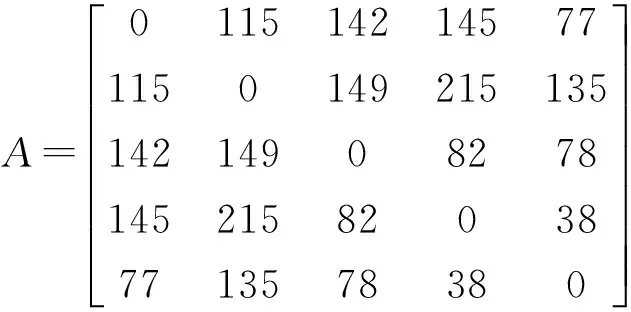
各参数计算结果:

D1=479、D2=614、D3=451、D4=480、D5=328、D=2352β1=0.1991、β2=0.1847、β3=0.2021、β4=0.1990、β5=0.2149K=0.968

结果分析,B1、B2、B3、B4、B5五个元素在三个证据中均有出现,采用DS法则获得的结果是肯定B2,否定其他元素,这与事实不符,采用本文方法获得的结果与事实比较一致,优于经典DS法则。

B2的置信度最高,且219μg/m3的D=115,小于其他浓度值的D,因此,融合结果为219μg/m3。

6 结语

本文给出了一种粉尘检测系统,结合粉尘检测原理,分析了粉尘颗粒在空间中的运动状态,获得粉尘浓度分布,依据粉尘浓度分布特点,提出一种适用于粉尘浓度数据的概率赋值函数获取方法,给出了一种新的融合方法,并通过计算与分析,验证了方法的合理性,在数据高度冲突时,融合结果符合实际情况,优于经典DS证据理论。

[1] Yager R R. On the D-S framework and new combina-tion rules[J]. Information Sciences,1987,41(2):93-138.

[2] 孙全,叶秀清,顾伟康.一种新的基于证据理论的合成公式[J].电子学报,2000,28(8):117-119. SUN Quan, YE Xiuqing, GU Weikang. A new synthesis formula based on evidence theory[J]. Journal of electronics,2000,28(8):117-119.

[3] Shafer G. A mathematical theory of evidence[M]. Princeton, N J: Princeton U P,1976:10-40.

[4] Dempster A P. Upper and lower probabilities induced by a multi-valued mapping[J]. Ann Mathematical Statistics,1967,38:325-339.

[5] 刘海燕,赵宗贵,刘熹:DS证据理论中冲突证据的合成方法[J].电子科技大学学报,2008,37(5):701-704. LIU Haiyan, ZHAO Zonggui, LIU Xi. DS evidence theory synthesis method of conflict evidence in[J]. Journal of University of Electronic Science and Technology,2008,37(5):701-704.

[6] 史超,程咏梅.基于证据冲突度的多传感器冲突信息组合方法[J].计算机应用研究,2011,28(3):865-868. SHI Chao, CHENG Yongmei. Based on the degree of evidence conflict conflict of multi-sensor information combination method[J]. Computer Application Research,2011,28(3):865-868.

[7] 邓勇,施文康.一种改进的证据推理组合规则[J].上海交通大学学报,2003,37(8):1275-1278. DENG Yong, SHI Wenkang. An improved evidence combination reasoning rule[J]. Journal of Shanghai Jiaotong University,2003,37(8):1275-1278.

[8] 王刚.证据理论及其在图像目标识别中的应用[D].西安:西北工业大学硕士论文,2002:78-83. WANG Gang. Evidence theory and its application in image target recognition[D]. Xi’an: Master Thesis of Northwestern Polytechnical University,2002:78-83.

[9] 赵宗贵,等.多传感器数据融合[M].北京:机械电子工业部第二十八研究所,1993,2:46-52. ZHAO Zonggui, et al. Compilation. Such as multi-sensor data fusion[M]. Beijing: Institute of Machinery and Electronics Industry of 28,1993:46-52.

[10] 马国清,赵亮,李鹏.基于Dempster-Shafer证据推理的多传感器信息融合技术及应用[J].现代电子技术,2003,19:41-44. MA Guoqing, ZHAO Liang, LI Peng. Based on the Dempster-Shafer evidential reasoning of multi-sensor information fusion technology and application[J]. Journal of Modern Electronic Technology,2003,12:41-44.

[11] 王玉茹,冯德振,张智杰.光散射法测烟尘浓度的实验研究[J].济南大学学报,2001,15(3):253-255. WANG Yuru, FENG Dezhen, ZHANG Zhijie. The experiment of measuring smoke concentration light scattering method research[J]. Journal of Jinan University,2001,15(3):253-255.

Dust Concentration Data Fusion Algorithm Based on DS Evidence Theory

JING Hang YU Xiaoning

(School of Electronic and Information Engineering, Xi’an Technological University, Xi’an 710021)

Due to the conflict issues can not be solved effectively when processing dust concentration data based on DS evidence theory, combined with dust detection theory, this paper analyzes the forces when dust particles are in space force, gets the movement of dust particles in space and diffusion process, obtains the distribution of dust concentration. According to the distribution of dust concentration, this paper presents probability assignment function acquisition method that is suitable for dust concentration data, proposes a new fusion rules to eliminate conflicts in the meantime.

DS evidence theory, dust concentration, conflicts

2016年9月8日,

2016年10月18日

陕西省教育厅2016年度专项科学研究计划(编号:16JK1368)资助。

景航,男,硕士研究生,研究方向:粉尘浓度检测。于小宁,男,工程师,研究方向:表面光散射。

TP391

10.3969/j.issn.1672-9722.2017.03.007