单幅运动模糊图像模糊核参数估计*

库鹏森 玉振明 彭国晋

(1.桂林电子科技大学信息与通信学院 桂林 541004)(2.梧州学院 梧州 543002)

单幅运动模糊图像模糊核参数估计*

库鹏森1玉振明2彭国晋2

(1.桂林电子科技大学信息与通信学院 桂林 541004)(2.梧州学院 梧州 543002)

针对模糊图像傅立叶变换过程由于边缘截断效应在频谱图中产生的十字亮线,和图像中心亮斑对模糊核估计精度干扰的问题,首先利用设计的模版腐蚀二值化倒频谱图,只保留十字亮线和中心亮斑。然后使用原始二值化频谱图减去仅包含十字亮线和中心亮斑的图像,达到剔除十字亮线和中心亮斑的目的,再对所得倒频谱图利用Radon变换准确估计出模糊角度。最后在上述基础之上,分析频谱图灰度变化估计出模糊长度。实验验证,该方法简单可行、精度高、抗噪能力强。

运动模糊; 倒频谱; Radon变换; 模糊核; 腐蚀

Class Number TN911.73

1 引言

在图像获取过程中,成像设备与目标之间的相对运动会引起成像模糊,称为运动模糊。由运动模糊造成的图像模糊严重影响对图像中所需信息的提取,使图像应用受到了极大阻碍,所以对模糊图像的复原就成了一个亟待解决的问题。模糊图像复原的关键在于对模糊图像点扩散函数的精确估计,而估计点扩散函数实质是对模糊图像模糊参数的估计,即模糊角度和模糊长度。因此模糊图像参数的准确估计对图像复原至关重要。

在频域对运动模糊图像参数估计的研究中,由于傅立叶变换的边缘截断效应,使频谱图中出现的十字亮线与图像中心亮斑都会严重影响到模糊参数的估计精度。针对此问题,A.M.Deshpande等[1]利用比特平面分层的方法进一步提取频谱图所包含的模糊参数信息以提高估计精度,但并没有提出剔除十字亮线和中心亮斑的实际解决方法。乐翔等[2]依据十字亮线位置对频谱图进行分块,再将分块后的频谱图按照一定阈值做反色处理,最后利用Radon变换估计模糊参数。该方法虽然有效避开了亮线干扰,估计精度也有所提高,但在分块过程中多次对频谱图的转换会影响到估计精度,其鲁棒性也较差。孔勇奇等[3]通过计算频谱图中每个像素邻域范围内像素灰度的平均值,然后利用滑动邻域操作的方法将十字亮线所处像素灰度置0,避免亮线对参数估计的干扰,而对亮斑未做任何处理。王琳等[4]提出使用频谱分块与边缘检测相结合的方法,避开亮线干扰。该方法在乐翔等方法的基础之上,改进了频谱图分块的条件,并利用边缘检测使分块更加精确。付强等[5]在小模糊尺度下,当图像大小为M×N时,根据M、N的奇偶情况将亮线所在行和列置0,达到剔除十字亮线的目的。

首先求出模糊图像倒频谱图,选取合适的阈值将倒频谱图做二值化处理。分析二值化频谱图中十字亮线和中心亮斑的成因及分布特点,利用二值形态学和图像加减法将其剔除,使用Radon变换绘制极值曲线,从而估计出模糊角度,再根据所得角度旋转频谱图至水平方向,并分析频谱图灰度值变化,绘制曲线图估计模糊长度。实验结果表明,该方法简单有效,精度高,且具有较好的鲁棒性。

2 运动模糊模型

成像过程中由于曝光时间很短,可近似认为成像设备与目标之间的相对运动是匀速直线运动。运动模糊图像是原始清晰图像与点扩散函数的卷积结果,再加一个加性噪声形成,可表示为

g(x,y)=f(x,y)*h(x,y)+n(x,y)

(1)

其中g(x,y)、f(x,y)、h(x,y)、n(x,y)分别表示模糊图像、原始图像、模糊核、加性噪声,*为卷积符号。

在没有噪声的情况,设T为曝光时间,令x0(t)和y0(t)分别表示在时间T内x和y方向上的运动分量,则运动模糊的退化过程可表示为

(2)

对式(2)做傅立叶变换得:

(3)

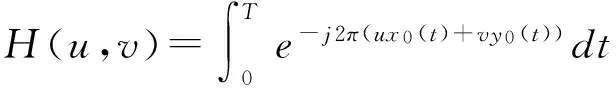
(4)

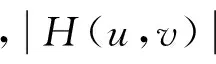
图1 运动模糊图像和频谱图

由PSF函数的频谱表达式可得出其在时域表达式为[7]

(5)

其中,L和θ分别表示模糊核函数的模糊长度和模糊角度。

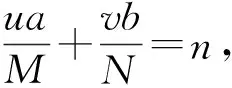
(6)

设模糊图像频谱图中心两条暗条纹间距为2d,设M=σN,则模糊长度为[8～9]

(7)

当M=N时,条纹倾斜角与模糊角度垂直,即：

(8)

同时模糊长度为

(9)

3 模糊参数估计

3.1 Radon变换原理

Radon变换是在一个平面内沿着不同直线做线积分的变换。对于二维图像函数g(x,y)的Radon变换定义为[10]

R(G)(ρ,θ)=

(10)

式中ρ表示直线l到原点的距离,θ表示l与y轴正方向的夹角,如图2所示。

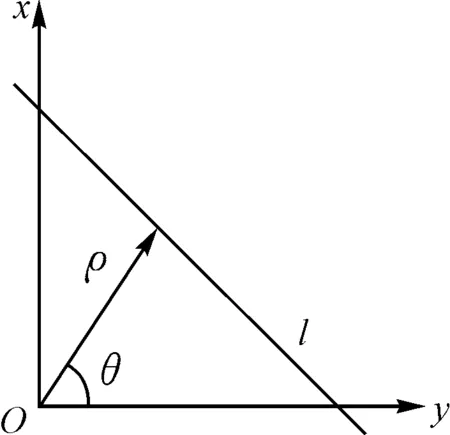
图2 Radon变换

3.2 模糊角度估计方法改进

在对运动模糊模型分析过程中已经指出,模糊图像的傅立叶频谱图会呈现出明暗相间的规律条纹,如图1(c)所示。但是由于傅立叶频谱图中存在诸多的噪点,且条纹特征并不是十分明显,直接利用Radon变换估计模糊角度误差较大。针对上述问题,采用倒频谱分离出更细化的模糊信息[11～12],同时将倒频谱一般定义改进为

(11)

在式(11)基础之上,对倒频谱再取对数进一步细化模糊信息,在倒频谱图中清晰显示出低频部分包含的模糊信息,如图1(d)所示。

为了更加准确地估计出模糊角度,对倒频谱做二值化处理。通过多次实验对比选取二值化阈值为0.011,对图1(d)二值化结果如图3(a)所示。

在图1(c)所示的模糊图像傅立叶频谱图中可以看到十分清晰的十字亮线,由于傅立叶变换中的边缘截断效应产生,在倒频谱图中更加清晰,如图3(a)所示。十字亮线的出现对模糊角度的估计会产生极大干扰。图3(a)中还可看见清晰的中心亮斑,而中心亮斑并不包含原始图像的方向特征信息[5],也会对估计造成干扰。

针对倒频谱图中十字亮线和中心亮斑对模糊角度估计干扰问题,本文利用二值形态学和图像加减的方法剔除十字亮线和中心亮斑。

十字亮线和中心亮斑在二值化后的倒频谱图中像素值为全1,排布十分规律,且与包含模糊角度的斜线排列不同。依此特点,设计出模版R=[1,1;1,0]对图3(a)进行腐蚀,只保留包含十字亮线的一个亮斑,如图3(b)所示。然后用原始二值化图3(a)减去腐蚀后的二值化图3(b),以达到剔除十字亮线和中心亮斑的目的,如图3(c)所示。

图3 剔除十字亮线和亮斑过程

剔除十字亮线和中心亮斑后利用Radon变换估计出图3(c)中斜线角度θ′,再通过式(12)修正估计出模糊角度θ。在Radon变换极值曲线中,极大值对应角度即为斜线角度θ′,如图4所示。

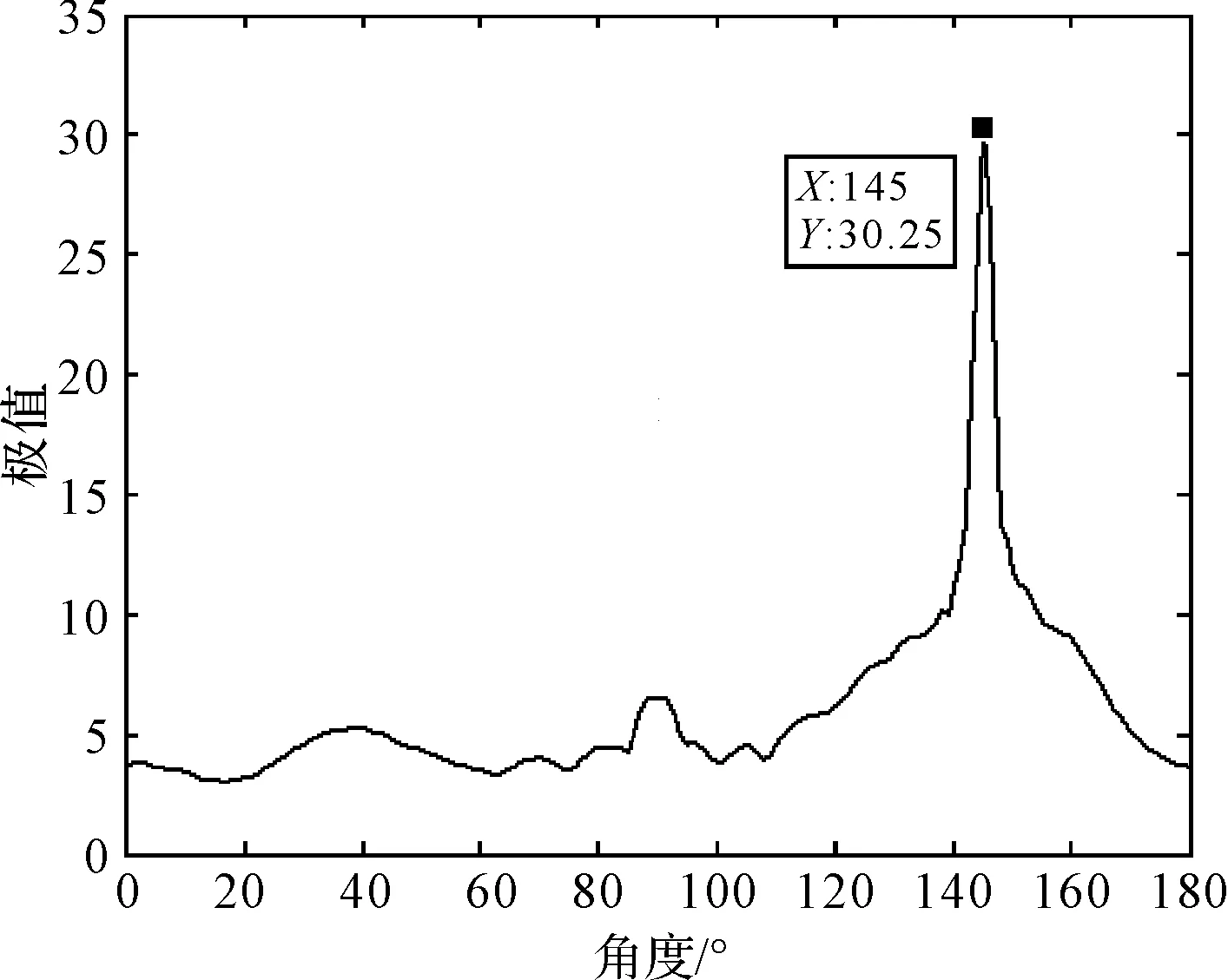
图4 Radon变换极值曲线(θ=55°)

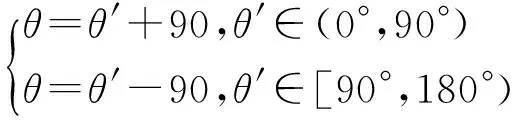
(12)

3.3 估计模糊长度

估计出模糊角度后,将傅立叶频谱图按照估计出的模糊角度旋转到水平方向的模糊,并将其剪切为与原图大小一致,如图5(a)所示。为了更准确地提取图像灰度值,截取图像中心条纹特征更明显的区域,如图5(b)所示。然后求出每列灰度值的和并做出曲线,如图5(c)所示。

在灰度曲线上,主瓣宽度即为频谱图中心两条暗条纹间距。最后利用主瓣和两个旁瓣间距的平均值作为条纹间距d,然后根据式(9)计算出模糊长度。

图5 旋转图和灰度曲线

3.4 算法实现

基于上述理论分析,算法实现步骤如下：

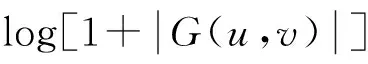
2) 将上述倒频谱图用阈值0.011做二值化处理。

3) 用模版R=[1,1;1,0]腐蚀2)中图像。

4) 用2)中图像减去3)中图像,剔除十字亮线和中心亮斑。

5) 在0°～180°对4)中图像做Radon变换,并绘制极大值曲线。并找出极大值对应角度,利用式(12)计算出模糊角度。

6) 根据5)所估计模糊角度,将频谱图G(u,v)旋转至水平方向的模糊,并截取中心条纹特征明显的区域。

7) 对6)中图像按列求灰度值的和,并绘制曲线,根据主瓣和旁瓣间距求取条纹间距d,并依据式(9)计算出模糊长度。

4 算法验证

在Matlab平台下,将大小为512×512的liftingbody标准图像作为实验图像,如图1(a)所示。在不同模糊长度和模糊角度下验证算法,模糊图像如图1(b)所示。实验估计模糊角度如表1所示,估计模糊长度如表2所示。

为了进一步说明算法的有效性,在不添加噪声的情况下,对多个模糊长度和模糊角度将本文算法与同类型算法做出比较,结果如表3所示。同时再利用估计出的模糊核参数对模糊图像使用维纳滤波进行恢复,图像信噪比设为0.001,与同类算法图像恢复结果对比如图6所示。利用文献[2]恢复过程中直接使用原模糊长度。

表1和表2的数据表明,算法将模糊长度估计误差控制在1个像素,模糊角度估计误差控制在0.05到0.49之间,充分说明了算法的有效性。同时表3数据和图6对模糊图像的恢复结果与同类算法的对比,表明了本文算法估计结果的准确性,优于同类算法。

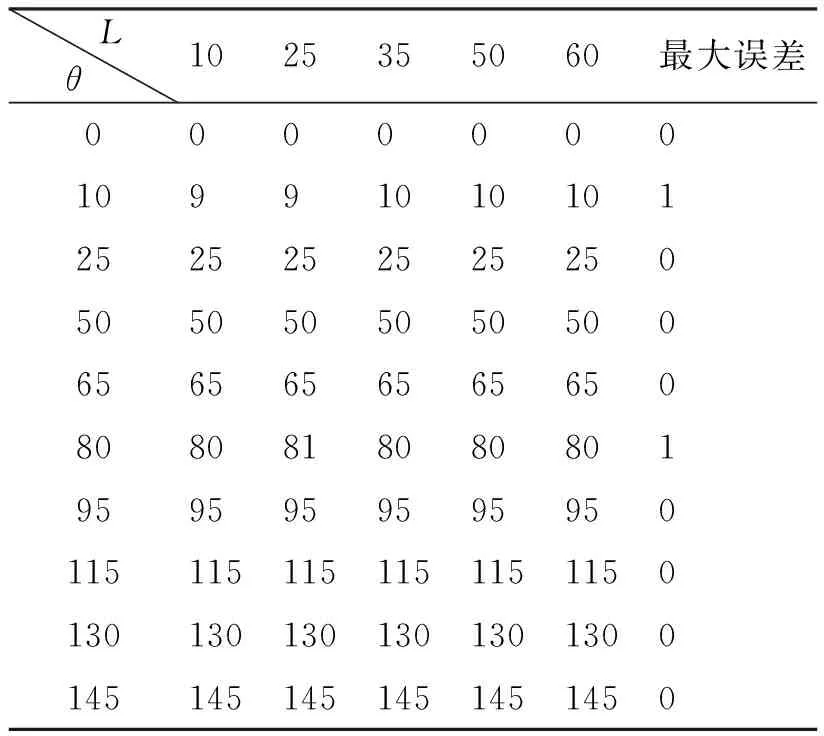
表1 模糊角度估计

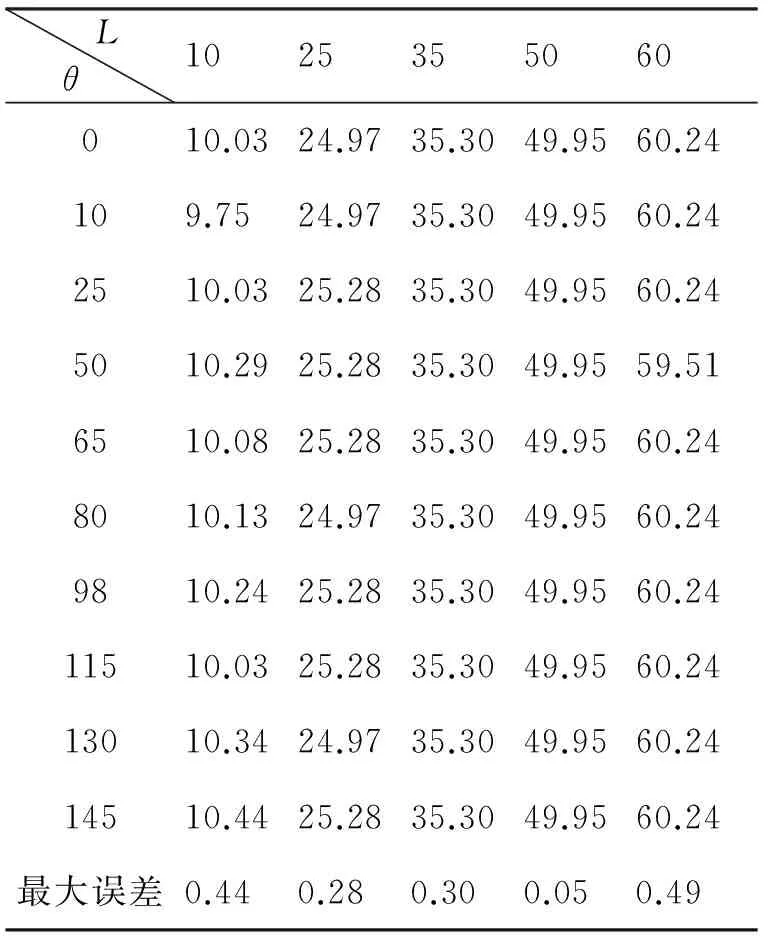
表2 模糊长度估计

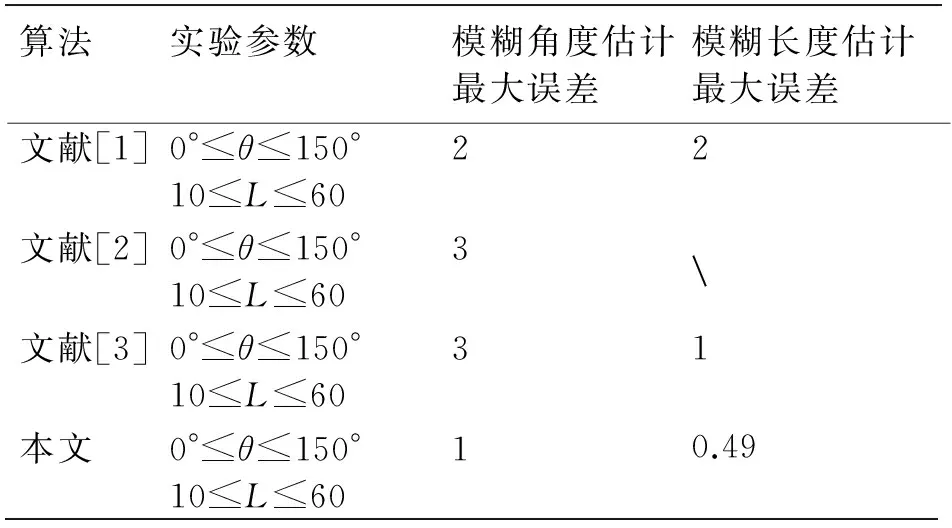
表3 算法对比

其中文献[2]没有说明模糊长度的估计方法。

图6 模糊图像维纳滤波恢复结果对比(实际模糊参数L=25,θ=50°)

5 结语

主要针对运动模糊图像倒频谱图中的十字亮线和中心亮斑,压缩频谱图灰度值,并分析其成因及分布特点并提出新的方法将其剔除,避免其对模糊参数估计的干扰。尽管实验验证该算法简单有效,但仍有不足之处,例如并没有将十字亮线完全剔除,可作为之后的研究重点,然后再将算法适用于任意尺寸的图像,进一步优化算法以提高估计精度和抗噪性,应用于实际采集的图像当中,验证算法在实际图像中的性能。

[1] Deshpande A M, Patnaik S. Single image motion deblurring: An accurate PSF estimation and ringing reduction[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(14):3612-3618.

[2] 乐翔,程建,李民.一种改进的基于Radon变换的运动模糊图像参数估计方法[J].红外与激光工程,2011,40(5):963-969. LE Xiang, CHENG Jian, LI Min. Improved approach to motion blur identification based on Radon transform[J]. Infrared and Laser Engineering,2011,40(5):963-969.

[3] 孔勇奇,卢敏,潘志庚.频谱预处理模糊运动方向鉴别的改进算法[J].中国图象图形学报,2013,18(6):637-646. KONG Yongqi, LU Min, PAN Zhigeng. Motion blur direction detection based on pre-processing of spectrum image[J]. Journal of image and Graphics,2013,18(6):637-646.

[4] 王琳,师雪艳,张少辉,等.基于Radon变换的遥感图像运动模糊参数精确估计[J].计算机应用研究,2015,32(12):3798-3800. WANG Lin, SHI Xueyan, ZHANG Shaohui, et al. Accurate estimation of remote sensing image motion blur parameters based on Radon transform[J]. Application Research of Computers,2015,32(12):3798-3800.

[5] 付强,孙秀霞,刘树光,等.小模糊尺度下运动模糊方向鉴别算法研究[J].应用光学,2015,36(5):748-754. FU Qiang, SUN Xiuxia, LIU Shuguang, et al. Novel accurate direction detection method of small-scate motion blurred image[J]. Journal of Applied Optics,2015,36(5):748-754.

[6] 贺卫国,黎绍发.匀速直线运动模糊长度的精确估计[J].计算机应用,2005,25(6):1316-1317. HE Weiguo, LI Shaofa. Estimating the blurring length of uniform linear motion blurred images[J]. Journal of Computer Applications,2005,25(6):1317-1317.

[7] Mishra S, Sengar R S, Puri R K, et al. Efficient motion blur parameters estimation under noisy conditions[C]//Computational Intelligence and Computing Research (IC-CIC), 2014 IEEE International Conference on. IEEE,2014.

[8] 李宇成,贾宝华,杨光明.运动模糊图像的参数估计与恢复[J].计算机工程与设计,2010,31(19):4247-4249. LI Yucheng, JIA Baohua, Yang Guangming. Blur parameter identification and restoration of motion blurred image[J]. Computer Engineering and Design,2010,31(19):4247-4249.

[9] Zhang P, Wang S, Fu D. Blind Estimation of Blur Parameters by 2D-DFT on Polar Coordinate System Presented on Rectangular Grids[C]// Seventh International Conference on Image and Graphics. 2013:95-98.

[10] Deshpande A M, Patnaik S. Radon trans-form based uniform and non-uniform motion blur parameter estimation[C]// Communication, Information & Computing Technology (ICCICT), 2012 International Conference on. IEEE, 2012:1-6.

[11] 王秋云.基于倒谱特性的运动模糊图像PSF参数估计[J].自动化与仪器仪表,2014(12):180-183. WANG Qiuyun. Cepstral feature based motion blur image PSF parameter estimation[J]. Automation & Instrumentation,2014(12):180-183.

[12] Shah M J, Dalal U D. Blind estimation of motion blur kernel parameters using Cepstral domain and Hough transform[C]//International Conference on Advances in Computing, Communications and Informatics,2014:992-997.

Blur Kernel Parameter Estimation of Single Motion Blurred Image

KU Pengsen1YU Zhenming2PENG Guojin2

(1. School of Information and Communication, Guilin University of Electronic and Technology, Guilin 541004) (2. Wuzhou University, Wuzhou 543002)

Aiming at the problem of the cross-shaped bright lines in the spectrum image due to the edge truncation effect of the Fourier transform and the bright spots which could interrupt the blur parameter estimation, the designed template erosion the binary image of Cepstrum is used to hold on the cross-shaped bright lines and bright spots. Then the original binary image of Cepstrum is used subtract the image which contains only the cross-shaped bright lines, remove the cross-shaped bright lines and bright spots, and then accurate estimation the blur angle of the image of Cepstrum based on Radon transform is conducted. Finally, based on the above fundamental theories, the gray scale change of spectrum image is analyzed to estimate the blur length. Experiments demonstrate that this method is simple, has high estimation accuracy, good robustness.

motion blur, Cepstrum, Radon transformation, blur kernel, erosion

2016年9月4日,

2016年10月24日

国家自然科学基金项目(编号:6156050342)资助。

库鹏森,男,硕士研究生,研究方向:运动图像模糊。玉振明,男,博士,教授,研究方向:图像融合,信号处理。彭国晋,男,硕士,助教,研究方向:视频图像处理。

TN911.73

10.3969/j.issn.1672-9722.2017.03.027