基于有序对的不确定XML小枝模式查询算法*

刘立新 王永平

(内蒙古科技大学信息工程学院 包头 014010)

基于有序对的不确定XML小枝模式查询算法*

刘立新 王永平

(内蒙古科技大学信息工程学院 包头 014010)

随着不确定数据的广泛应用,不确定数据管理成为一个重要的研究方向。针对目前不确定XML小枝模式查询技术并没有很好解决含父子关系的查询,论文提出基于有序对的ProOPCTwig算法。该算法以有序对的形式存储查询树和P-文档,通过查询树标签流的流指针所指节点的有序对和P-文档中该结点标签流中的节点有序对来进行匹配进行查询。有效处理了不确定XML中的分布节点、查询结果概率的计算。且在有序对匹配时不需要逐条扫描删除,提高匹配速度。理论分析和实验结果证明了ProOPCTwig算法的查询效率。

不确定XML数据; P-文档; 小枝模式; 父子关系; 有序对

Class Number TP312.2

1 引言

不确定性数据在经济、军事、物流、金融、电信等领域中普遍存在[1],离散型不确定数据通常是以一定概率出现的离散值,连续型不确定数据常用概率密度函数表示[2～3]。半结构化数据XML以其灵活性、可扩展性、自描述性等特点为不确定数据提供了更自然的表达方式。概率XML数据是近年来提出的一种新的不确定数据表示方法,目前应用概率XML管理不确定数据已经取得一系列的研究成果,包括概率XML数据模型、概率XML代数和查询[4]、关键字查询[5～6]、原型系统等内容,其中概率XML小枝模式查询是其中一个重要的分支。

不确定XML小枝模式查询,即Twig Pattern查询,是概率XML查询处理的重要方法,目前大多算法是扩展普通XML小枝模式查询。文献[7]根据查询语义将小枝模式查询分为布尔查询语义、完全语义查询和不完全语义查询。文献[8]扩展区间编码后使用整体小枝模式的方法查询,需要存储中间结果和归并中间结果。考虑概率小的查询结果可能没有意义,文献[9]扩展杜威编码查找大于一定概率阈值的小枝模式,采用两步过滤策略加快查询。文献[10]扩展杜威编码查找概率值最大的Top-K小枝模式,并采用按概率大小对元素流进行排序的方法来提高查询效率。

上述关于概率XML小枝模式查询算法并不能很好处理父子关系。在普通XML小枝模式查询处理算法中,Twigstacklist算法[11]通过向前看的策略能较好地处理小枝模式中的父子关系,但当分支结点含父子关系时,仍有中间结果产生。陶[12～13]提出了基于有序对的算法处理父子关系,能克服Twigstacklist算法中存在的问题,但是有序对匹配时查找效率低。针对上述问题,本文提出基于有序对的不确定XML小枝模式查询算法,重点研究基于有序对处理概率XML小枝模式查询时分布节点的处理、查询结果概率的计算以及有序对匹配效率的提高等问题。最后通过大量实验分析了所提出的ProOPCTwig算法的效率。

2 相关知识

2.1 数据模型

目前概率XML数据模型主要包括P-文档、PXDB、PXML、PrXML等,其中P-文档是其他几种模型的基础,目前大多数概率XML数据查询处理都是基于P-文档模型。

在P-文档模型中有普通节点和分布式节点两种类型的节点。每一个普通节点都有一个标签和一个唯一的标识符,普通节点可能出现在样本空间的文件中,分布式节点仅用于定义产生随机文件的概率过程。分布式节点有[14]: 1) 独立分布节点ind,其孩子节点在P-文档树中的存在互相独立,互不影响。 2) 互斥分布节点mux,其孩子只能出现一个,或者全部都不出现。 3) 事件驱动节点cie,其孩子节点的存在是互相独立的,每个节点的存在由外部事件变量e1,e2,…,en所决定,对应一个外部事件。 4) 组合节点exp,它包含多个孩子节点,可选择不同的孩子节点组成exp节点集合,且所有孩子节点的存在概率和为1。 5) 确定型节点det,这种节点类型是上述四种节点类型的特例,它要求确定型节点的所有孩子节点必须存在。 6) 连续概率分布节点cont,cont描述当前节点的孩子节点分布情况符合哪种连续概率分布曲线,如二项分布、高斯分布和泊松分布等,存储概率密度函数及其参数。在上述六种分布节点类型中,独立分布节点和互斥分布节点类型所组成的模型应用最为广泛。

在P-文档模型中概率值附加到文档树的边上,各节点的概率依赖于其祖先的概率。一条边e的权重,记为Pr(e),它表示分布节点选择孩子节点的概率。在P-文档中,一个节点Vi在文档中出现的概率等于从根节点到节点Vi经过的所有的边的概率的乘积。图1为一包含mux,ind两种类型的分布节点的P-文档,可表示为PrXMLmux,ind,节点B1出现的概率Pr(B1)=0.2*0.3=0.06。

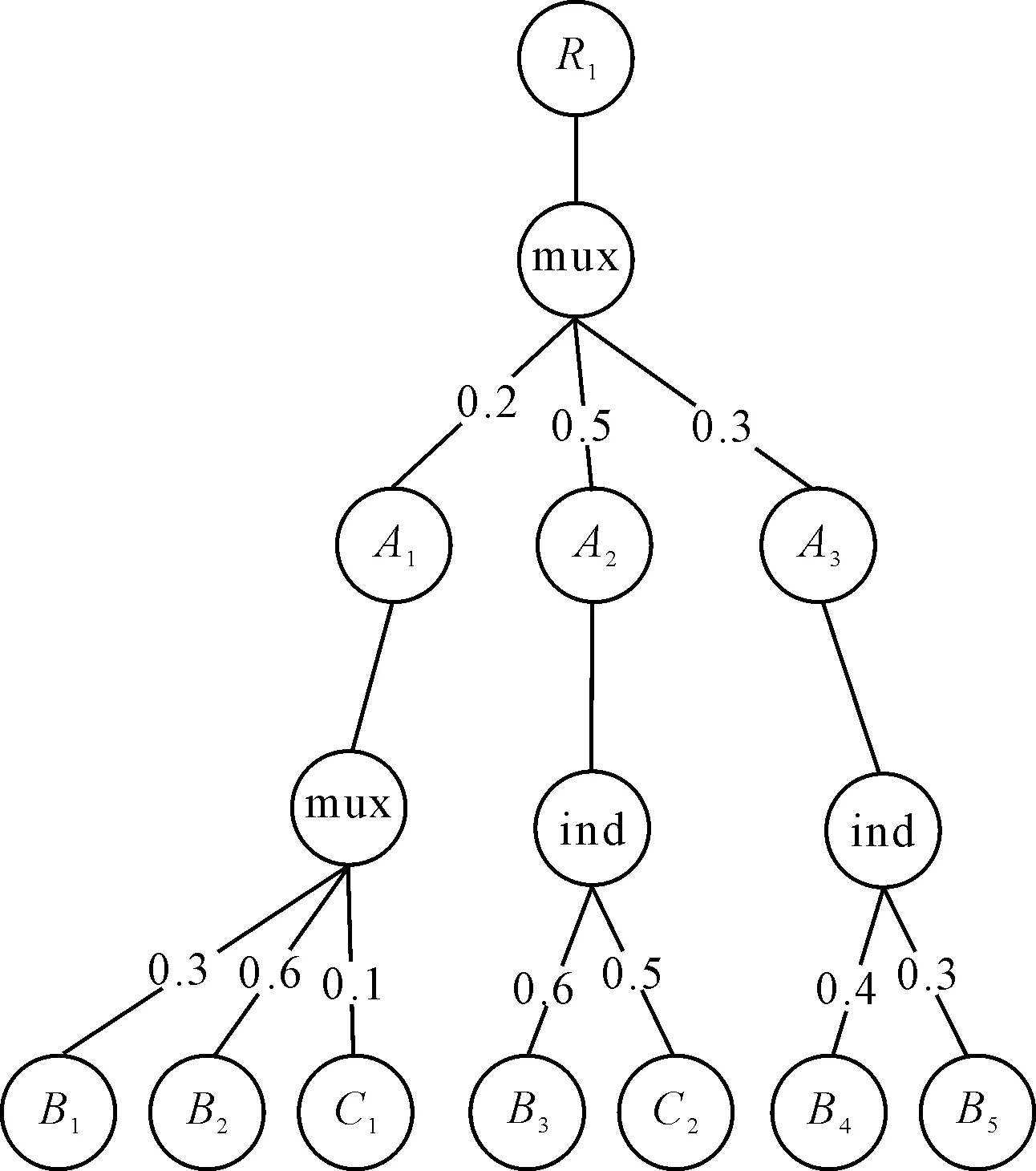
图1 P-文档示例

2.2 不确定XML小枝模式查询

不确定XML小枝模式查询不仅需要在包含分布节点的概率XML数据中找出满足小枝模式出现的所有匹配结果,而且同时还需要计算每个结果的概率值。为描述清晰,文中以带下标的大写字母表示P-文档中的元素节点,以大写字母表示小枝模式中的查询节点。

定义1 不确定XML小枝模式查询:给定一个小枝模式查询Q=(V,E)和一个P-文档D=(VD,ED),其中V和E分别表示小枝模式中的节点集合和边集合,VD和ED分别表示P-文档中的节点集合和边集合。小枝模式匹配就是在D上匹配Q的过程,是Q中的查询节点到D中的元素节点的映射过程,满足以下条件:

1) 对于每一个查询节点X∈V,VD中的元素节点Xi与X具有相同的标签名,且满足X的谓词约束。

2)VD中的元素节点Xi和Yj之间的关系必须满足V中相应查询节点X和Y之间的结构约束关系,如P-C关系、A-D关系。

3) 计算查询结果出现的概率值。

图2是XPath为R/A[/C]/B对应的小枝模式Q′,Q′在图1的P-文档上的一个查询结果是(R1,A2,B3,C2),出现的概率:0.5*0.6*0.5=0.15。而(R1,A2,B1,C1)不是查询结果,因为B1,C1是同一个互斥分布节点mux的孩子,不能同时存在。

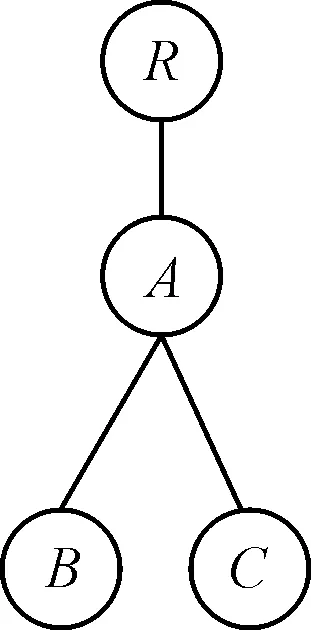
图2 小枝模式Q′

2.3 有序对

定义2 结点有序对:在查询树中,某个结点的结点有序对是由该结点和其父亲结点按先后顺序组成,记做(结点,父亲结点),没有父亲结点的设置父亲结点为null。但在,在P-文档中,分布节点不参与有序对的存储,则结点有序对为(结点,从根结点到此结点的路径上最近的普通结点),没有父亲结点的设置父亲结点为null,例如:(A1,R1)。

定义3 查询树标签流:按后序遍历查询树中结点的顺序排列,由查询树中所有结点对应的结点有序对组成。例如在图2中的Q′的标签流是(B,A),(C,A),(A,R),(R,null)。

定义4 元素结点标签流:在P-文档中,一个元素结点标签流是指按先序遍历P-文档中该类型结点的顺序排列,由所有该类型结点对应的结点有序对组成。例如Q′中A结点的元素结点标签流对应P-文档中的元素结点标签流为(A1,R1),(A2,R1),(A3,R1)。

3 基于有序对的不确定XML小枝模式查询算法

3.1 数据存储

为查询树建立一个查询表Query(name,pname,pnum,flag,level),存放所有查询结点的相关信息,采取查询结点按层遍历查询树并由底向上的顺序进入表。在表中,name表示当前节点类型,pname表示其父节点类型,pnum表示父节点的分支数,当在表中同一父节点分支数不为1且出现次数等于分支数时flag值为当前父节点类型,否则flag的值为null。level表示节点的层数,根节点所在的层数为1。例如Q′对应的查询表如表1所示。

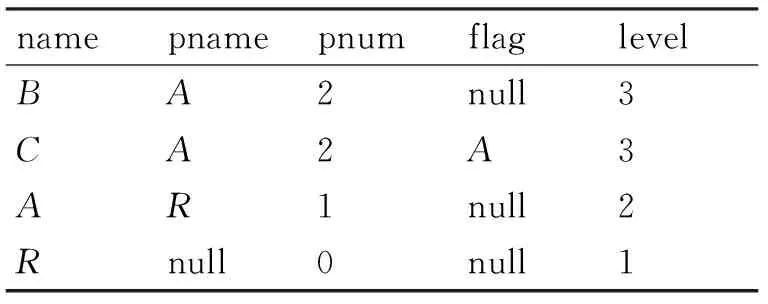
表1 Q′对应的查询表Query

为不同类型的节点分别建立文档表Document(name,id,pname,pid,path,pro),存放其所有结点的信息,结点按照先序遍历P-文档的顺序进入表。其中,name和pname分别指当前节点类型和其父节点类型,id指当前节点的编号,pid指父节点的编号,path表示由父节点到当前节点经过的分布节点,pro为父节点到当前节点的概率值。图1中P-文档对应的文档表如表2～表5所示。

表2 图1中P-文档R类型节点对应的文档表

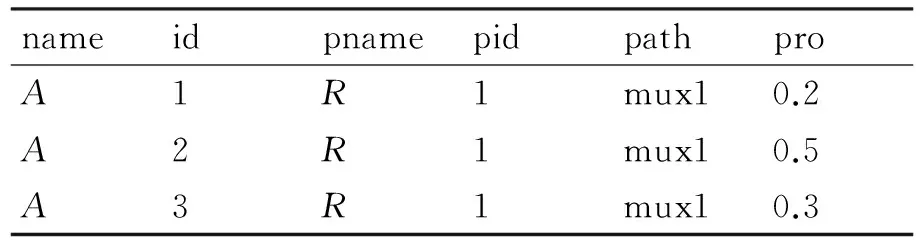
表3 图1中P-文档A类型节点对应的文档表

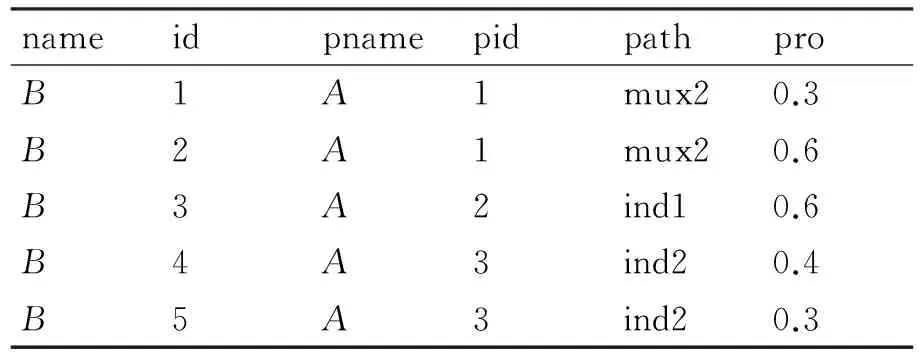
表4 图1中P-文档B类型节点对应的文档表

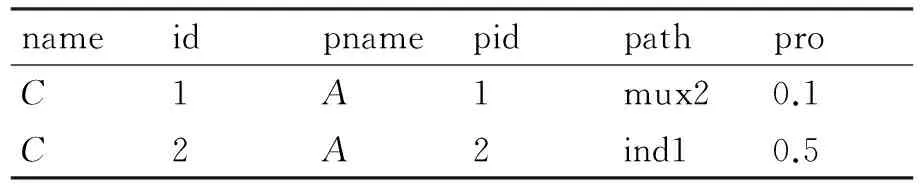
表5 图1中P-文档C类型节点对应的文档表

3.2 算法描述

ProOPCTwig算法是基于上述查询表和文档表进行查询的,通过查询树标签流的流指针所指节点的有序对和P-文档中该结点标签流中的节点有序对来进行匹配进行查询。由于查询表是按层遍历由底向上入表的,保证了它之前的节点有序对是匹配的,从而避免了无用结果的产生。例如,当Q′标签流所指节点有序对为(B,A),在P-文档中的节点有序对为(B1,A1)(B2,A1),(B3,A2),(B4,A3)(B5,A3),通过相应的匹配方法进行查询。

查询树中结点分为叶子节点、根节点和中间结点。叶子节点在P-文档对应的查询表中找到匹配的有序对中可能存在无用的有序对,这是因为分布节点mux的存在、以及其父亲结点是否包含其应该包含的所有叶子节点。而对于中间结点,由于处理时先序遍历查询表,保证了在处理中间结点前已经处理了其所有孩子节点,可以根据中间结点是否包含了所有的应该包含的孩子节点,来删除其孩子节点匹配时得到的有序对中的无用的有序对。对于根节点,只要保证其有所有的孩子节点,即可以得到最后的匹配结果。

当给定小枝模式Q和P-文档,得到对应的查询表Query和文档表,并得到Q的层数为m。ProOPCTwig算法主要步骤如下:

1) 指针P指向查询表Query的第一个元素。

2) 找到与P指向元素name相等的节点对应的文档表,利用该文档表进行有序对匹配,利用匹配结果初始化u。

3) 若P指向元素的flag不为null,P指针后移,找到与P指向元素name相等节点对应文档表,利用该文档表中进行有序对匹配,并利用匹配结果初始化v,合并u和v得到新的u。

4) 重复3)将u加入中间结果链表Lm中,P指针后移。

5) 若P指向元素层数为m,重复2)～4);m=m-1。

6) (a)若P指向元素为叶子节点,找到与P指向元素name相等的节点对应的文档表,利用该文档表进行有序对匹配,利用匹配结果初始化x。(b)否则,P指向元素为中间节点,找到与P指向元素name相等的节点对应的文档表,利用该文档表进行有序对匹配,利用匹配结果初始化x,根据Lm+1中元素更新x。

7) 若P指向元素的flag不为null,P指针后移,找到与P指向元素中name相等节点对应的文档表。若P指向元素为叶子节点,利用6)(a)初始化y,否则利用6)(b)初始化y;合并x,y得到新x。

8) 重复7),将x加入到中间链表Lm中,P指针后移。

9) 若P指向元素的层数m,重复6)～8);m=m-1。

10) 重复6)～9),直到P指向元素为空。

上述步骤中,1)～5)为处理第m层的节点,每次合并u和v得到新的u继续合并,结果保存在Lm中。6)开始由底层向上处理,(a)为中间层节点中叶子节点的情况(b)中间层节点中非叶子节点的情况,此时要考虑其上有父亲节点匹配和下有孩子节点的匹配问题。7)～9)实现循环处理中间层节点,直至根节点处理完毕,即查询表为空为止。

算法中每当合并节点时,要考虑待处理的节点下面是否含有分布结点。如果含有ind节点,则待处理节点的孩子节点可以同时出现,可以继续向上匹配;如果是mux节点,说明待处理节点的孩子节点不可以同时出现,停止关于此节点的查询。

为提高匹配效率,结点在查询过程中,为P-文档中与它匹配的节点有序对建立hash表并以有序对中父结点的name和id为关键值。这样,当发现某个中间结点不包含它应该包含的所有的孩子节点时,可以删除对应的hash表中的几条记录,不用逐条扫描删除记录。

最后得到的每一个匹配结果都是以一定概率值出现,此概率值可以通过文档表中存储的概率信息来计算,即为得到的有序对的概率的乘积。

3.3 算法举例

以图1的P-文档图2的小枝模式Q′为例来说明ProOPCTwig算法的工作原理,执行步骤如下:

1)P指针指向查询表中(B,A),进行有序对(B,A)匹配。到B节点对应的文档表去进行匹配,得:

A1(mux2,B1)(mux2,B2)

A2(ind1,B3)

A3(ind2,B4)(ind2,B5)

2) 此时flag为null,P指针继续后移,进行有序对(C,A)匹配。到C节点对应的文档表去进行匹配,得:

A1(mux2,C1)

A2(ind1,C2)

此时flag不为null,合并结果,得到中间结果A2(ind1,B3,C2),概率为0.3。

3)P指针继续后移,进行有序对(A,R)匹配,A为中间节点,到A节点对应的文档表去进行匹配,得:

R1(mux1,A1)(mux1,A2)(mux1,A3)

此时,R的所有孩子节点已经匹配结束。需要寻找可以和2)得到的中间结果可以匹配的结果,可以得出R1(mux1,A2)可以匹配。在此合并,得R1(mux1,A2(ind1,B2,C2)),概率为0.15。

4)P指针继续后续,进行有序对(R,null)匹配,得到最终结果R1(A2,(B3,C2)),最终概率为0.15。

3.4 算法分析

ProOPCTwig算法可以输出整个小枝模式的匹配结果。目前大多数算法都需要对P-文档中结点进行编码和对查询语句的解析,ProOPCTwig算法采用把P-文档和查询语句存入表格的方法,效率相当,所以这里不考虑构造表的时间和空间开销,只考虑算法的查询效率。

有n个节点的小枝模式查询,最坏的情况下,ProOPCTwig算法的时间复杂度与n个查询节点对应的元素节点标签流Tq的大小和最后匹配结果大小总和成线性关系,即O(|T1|+…+|Ten|+|output|)。ProOPCTwig算法的空间复杂度最坏的情况下是查询树标签流和他对应元素节点标签流匹配节点的大小。

4 实验结果与分析

实验分为有序对匹配效率分析和ProOPCTwig算法效率分析。实验的硬件环境为:CPU Inter(R) Core i3(3.2GHz),RAM为4G,操作系统为64位的Windows 7旗舰版SP-1,实验工具为Eclipse SDK 3.7.1,JDK 6.0。实验采用DBLP作为测试数据集,由于原始DBLP数据集不包括概率分布信息,根据文献[15]中的方法对DBLP进行转换得到概率XML数据集。实验中使用五个不同的小枝模式查询,查询用例见表6。

表6 实验中用到的小枝模式查询用列表

4.1 有序对匹配效率对比分析

为准确分析有序对匹配的效率,本文同时实现文献[13]中的PCTwig算法。鉴于PCTwig算法是在普通XML中处理父子关系查询并不需要计算查询结果的概率,所以实验一和实验二采用原始的数据集DBLP;并且ProOPCTwig算法暂时除去和分布节点及概率处理相关部分(简称OPCTwig算法)。对比OPCTwig算法和PCTwig算法的查询效率

实验一:采用原始DBLP数据集(大小为56.4M),小枝查询模式变化(Q1～Q5)。对比测试OPCTwig算法和PCTwig算法的有序对匹配效率,实验结果如图3所示。

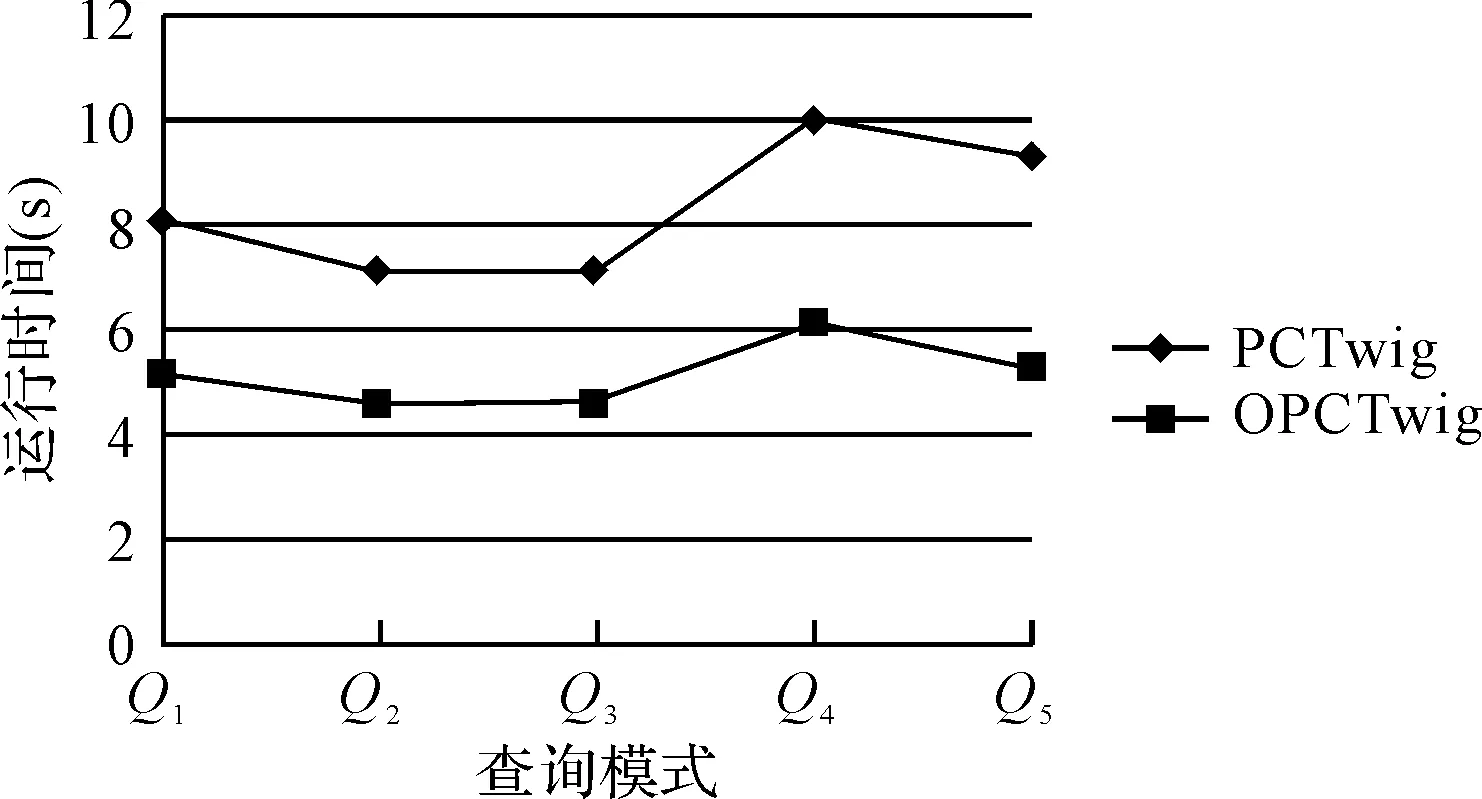
图3 不同查询模式下两算法运行时间比较

实验二:采用原始DBLP数据集(大小变化),小枝模式查询固定(以Q1为例),对比测试OPCTwig算法和PCTwig算法的有序对匹配效率,实验结果如图4所示。

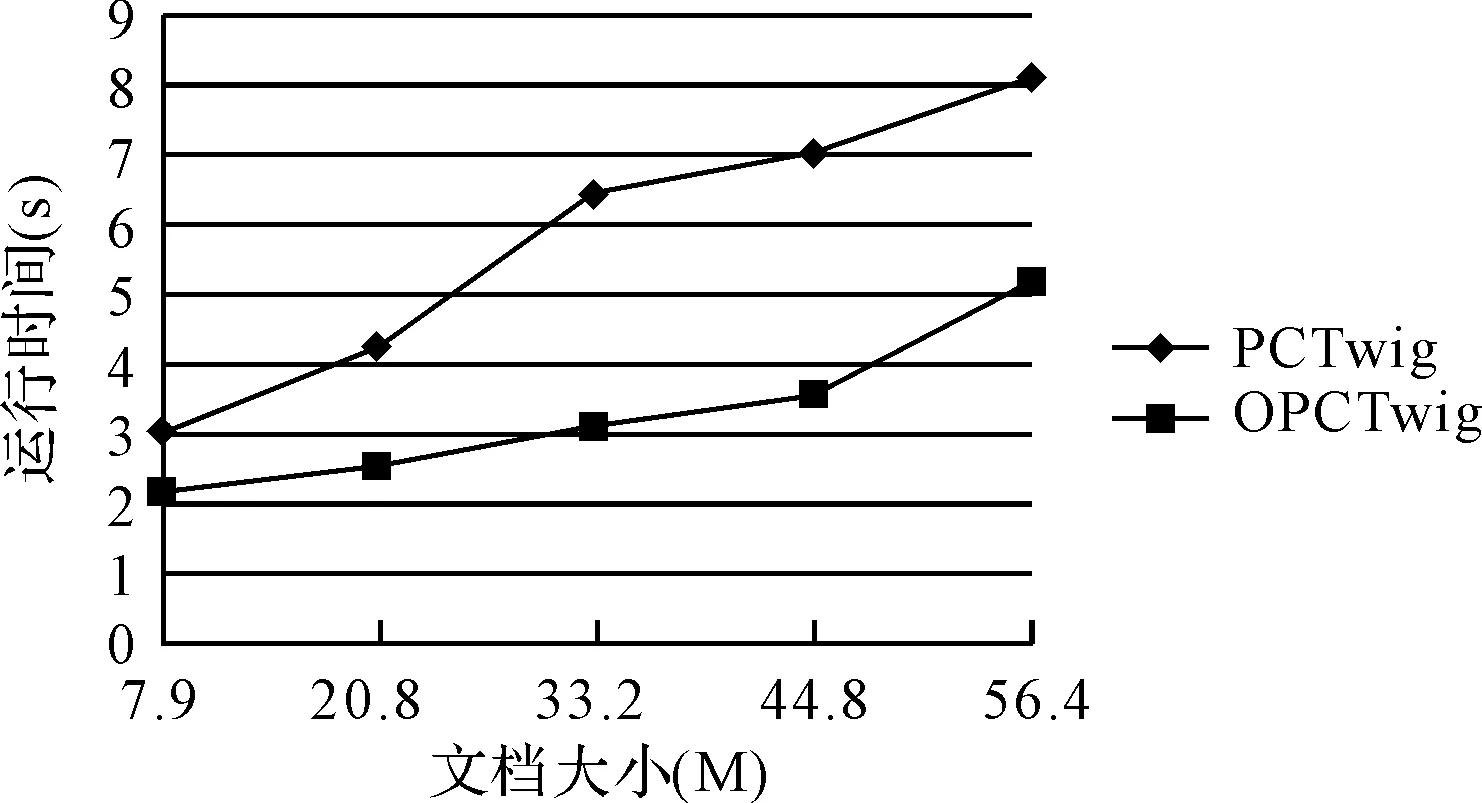
图4 不同大小数据集下两算法运行时间比较

实验一测试在文档相同而查询模式不同情况下,两算法的对比效率。实验二测试查询模式相同(以Q1为例)而文档大小不同时,两算法的效率。可以看出OPCTwig算法查找速度明显优于PCTwig算法,这是因为OPCTwig算法当遇到不匹配的有序对时,可以同时删除几条记录,而不需要逐条扫描删除,提高了有序对匹配效率。

4.2 ProOPCTwig算法的查询效率分析

为测试ProOPCTwig算法在不确定XML数据中处理父子关系的查询效率,实验数据集采用在DBLP数据集中随机插入分布节点形成P-文档。查询时仍采用表6中的小枝模式。

实验三:采用转换后的DBLP数据集。P-文档大小固定(大小为56.4M),小枝查询模式变化(Q1～Q5),测试ProOPCTwig算法的查询效率,实验结果如图5所示。

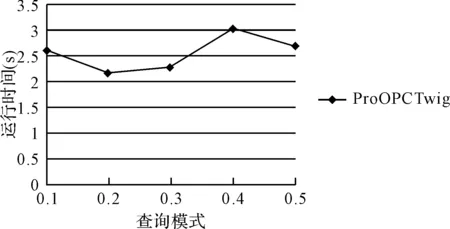
图5 不同查询模式下ProOPCTwig算法的查询效率

实验四:采用转换后的DBLP数据集。P-文档大小变化,小枝查询模式固定(以Q1为例),测试ProOPCTwig算法的查询效率,实验结果如图6所示。

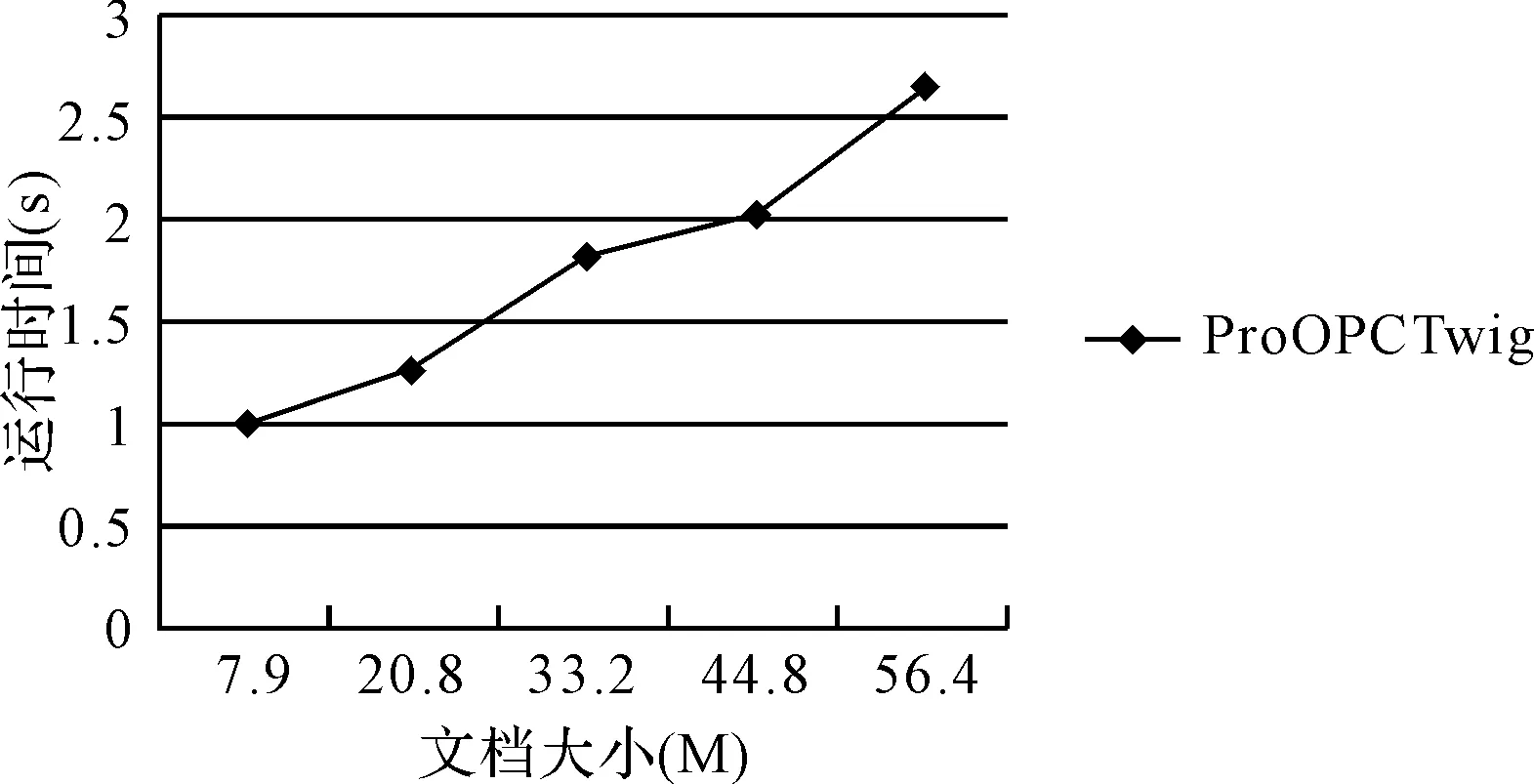
图6 不同大小文档下ProOPCTwig算法的查询效率

实验三和实验四分别在P-文档相同而查询语句不同,和P-文档不同而查询语句相同的情况下测试ProOPCTwig算法的查询效率,实验结果表明ProOPCTwig算法能有效处理不确定XML中包含父子关系的小枝模式查询。实验一、二和实验三、四的运行时间相差很大,这是因为不确定XML中分布节点的存在,使得符合条件的查询结果减少。

5 结语

本文提出基于有序对的不确定XML小枝模式查询算法ProOPCTwig。该算法不需要结构连接和归并操作,且在有序对匹配时可以同时删除几条数据,而不需要逐条扫描,大大提高有序对匹配效率,在处理不确定XML仅含父子关系的小枝模式查询时非常有效的。该算法的局限性是只能处理含父子边的小枝模式进行查询,下一步的工作目标是: 1) 基于有序对处理包含祖先后代关系的小枝模式; 2) 基于有序对处理包含谓词的复杂的小枝模式查询。

[1] 周傲英,金澈清,王国仁,等.不确定性数据管理技术研究综述[J].计算机学报,2009,32(1):1-16. ZHOU Aoying, JIN Cheqing, WANG Guoren, et al. A Surey on the Management of Uncertain Data[J]. Chinese Journal of Computer,2009,32(1):1-16.

[2] 李文凤,彭智勇,李德毅.不确定性Top-k查询处理[J].软件学报,2012,26(3):1-19. LI Wenfeng, PENG Zhiyong, LI Deyi. Top-k Query Processing Techniques on Uncertain Data[J]. Journal of Software,2012,26(3):1-19.

[3] LI Jian, Amol Deshpande. Ranking Continuous Probabilistic Datasets[C]//Proceeding of the 36thInternational Conference on Very Large Data Bases.Singapore: VLDB Endowment,2010:13-17.

[4] 张晓琳,郑珍珍,刘立新.连续概率XML数据查询处理技术[J].计算机工程与科学,2012,34(12):134-139. ZHANG Xiaolin, ZHENG Zhenzhen, LIU Lixin. Query Processing Techniques on Continuous Probabilistic XML Data[J]. Computer Engineering and Science,2012,34(12):134-139.

[5] 张晨静,王晓玲,周傲英.基于概率的SCLA的XML过滤[J].计算机学报,2014,37(9):1959-1971. ZHANG Chenjing, WANG Xiaoling, ZHOU Aoying. Filtering SLCA on Probabilistic XML[J]. Journal of Computers,2014,37(9):1959-1971.

[6] 周小平,史一民,张俊.概率XML文档Top-k关键字并行检索算法[J].计算机科学,2013,40(3):232-236. ZHOU Xiaoping, SHI Yimin, ZHANG Jun. Parallel algorithm of Top-k keyword query on Probabilistic XML document[J]. Computer Science,2013,40(3):232-236.

[7] Benny Kimelfeld, Yehoshua Sagiv. Matching Twigs in Probabilistic XML[C]//Proceeding of the 33thInternational Conference on Very Large Data Bases. Vienna: VLDB Endowment,2007:23-28.

[8] LI Yawen, WANG Guoren, XIN Juanchang. Holistically Twig Matching in Probabilistic XML[C]//Proceedings of the 25th International Conference on Data Engineering. Shanghai: IEEE,2009:1649-1656.

[9] LIU Siqi, WANG Guoren. Boosting Twig Joins in Probabilistic XML[C]//Proceeding of the 22ed International Conference on Database and Expert Systems Applications. France: Springer-Verlag,2011:51-58.

[10] Bo Ning, LIU Chengfei, Jeffrey Xu Yu, et al. Matching Top-k Answers of Twig Patterns in Probabilistic XML[C]//Proceeding of the 15th International Conference on Database Systems for Advanced Applications. Tsukuba: Springer-Verlag,2010:125-139.

[11] LU Jiaheng, CHEN Ting, Ling T W. Efficient processing of XML twig patterns with parent child edges: A look-ahead approach[C]//Proc of the ACM conference on information and Knowledge Management. New York: ACM,2004:533-542.

[12] 王瑞,陶世群.一种基于有序对的小枝模式匹配算法[J].计算机研究与发展,2009,46(Suppl.):69-73. WANG Rui, TAO Shiqun. A Match Algorithm for Twig Patterns Based on Ordered Pair[J]. Journal Of Computer Research and Development,2009,46(Suppl.):69-73.

[13] 王瑞,陶世群.一种基于有序对的含父子边的小枝模式匹配算法[J].计算机应用,2009,10(3):2778-2780. WANG Rui, TAO Shiqun. Matching Algorithm for Twig Pattern with Parent-Child Edges based on ordered pair[J]. Journal of Computer Applications,2009,10(3):2778-2780.

[14] Nierman A, Jagadish H V. Probabilistic data in XML[C]//Proceeding of the 28th international conference on Very Large Data Bases, Hong Kong: Springer-Verlag,2002:646-657.

[15] Kimelfeld B, Sagiv Y. Modeling and querying probabilistic XML data[J]. SIGMOD Record,2008,37(4):69-77.

Matching Twig Patterns in Uncertain XML Based on Ordered Pair

LIU Lixin WANG Yongping

(Information Engineering School, Inner Mongolia University of Science and Technology, Baotou 014010)

As the current uncertain XML twig pattern queries do not solve the patent-child relationship effectively, this paper proposes ProOPCTwig algorithms based on ordered pair. The algorithm stores query tree and P-document by ordered pair. It compares the ordered pair of query tree pointed by pointer of stream nodes and the ordered pair with the same label in P-document to query. The main works include dealing with the distributed nodes effectively, calculating probability of every result, and improving efficiency of matching ordered pair. Theoretical analysis and experimental results prove the efficiency of ProOPCTwig.

uncertain XML data, P-document, twig pattern, patent-child relationship, ordered pair

2016年9月3日,

2016年10月17日

国家自然科学基金:连续不确定XML数据管理关键技术研究(编号:61163015);内蒙古高等学校科学研究项目:云计算环境下海量XML数据关键字查询处理技术研究(编号:NJZY143);内蒙古科技大学创新基金(编号:2014QDL046)资助。

刘立新,女,硕士,讲师,研究方向:数据挖掘,数据库技术。

TP312.2

10.3969/j.issn.1672-9722.2017.03.018