阵列式射频仿真系统模拟大视场角方法研究*
2017-03-31刘志永褚建川
刘志永 褚建川 许 轲
(1.航空制导武器航空科技重点实验室 洛阳 471099)(2.中国空空导弹研究院 洛阳 471099)
阵列式射频仿真系统模拟大视场角方法研究*
刘志永1,2褚建川1,2许 轲1,2
(1.航空制导武器航空科技重点实验室 洛阳 471099)(2.中国空空导弹研究院 洛阳 471099)
阵列式射频仿真系统是验证导弹性能的重要手段。针对仿真试验过程中,由于天线阵列的目标角度模拟范围受限,论文分别介绍了天线阵列和转台所做相应设置来解决这一问题,通过这些设计有效地扩大了阵列式仿真系统目标角度模拟能力,并通过仿真试验验证了文章观点的正确性。
阵列式射频仿真系统; 目标角度模拟; 飞行转台设置
Class Number TP311
1 引言
阵列式射频仿真系统是验证导弹性能的主要验证手段,某阵列式射频仿真系统如图1所示[1],其中三轴转台和和阵列式天线阵列是射频仿真系统的关键设备,三轴转台主要是模拟导弹在空中飞行时姿态的变化,而阵列式天线阵列主要模拟目标的角运动。这样,导弹和目标的相对角运动在暗室的电磁环境中,可以逼真地模拟外场环境下的弹目运动,在这里进行半实物仿真,可以评估雷达制导导弹的作战性能。
但是在阵列式射频仿真系统中,由于试验设备的物理硬件的限制,目标相对于导弹的视线角往往局限在较小的范围内,使得某些发射条件无法得到满足,为了解决此类问题,本文通过分析各个坐标系之间的关系,通过数学剖析的方法来分析问题,从而分别设计转台的驱动方法和阵列式天线角度设置,通过这些设计,解决了导弹视线角受限问题,扩大了阵列式射频仿真系统的模拟能力。
2 阵列式射频仿真系统视线角受限分析
在阵列式射频仿真系统中,目标信号的模拟是通过阵列天线辐射电磁波来实现的。目标阵列有圆形阵列、六角形阵列、带状阵和混合阵等形式,某阵列式射频天线为六角形天线阵列。在通常情况下,在进行仿真试验时,以目标天线阵列的几何中心为目标初始位置,随着弹道的进行,目标的轨迹如图2中的实线1所示。但是,随着某些弹道的特殊需要,设计人员往往需要的目标轨迹如图2中虚线2所示,这超出了阵列的范围,就无法达到验证弹道的目的。

图1 阵列式射频仿真系统的组成
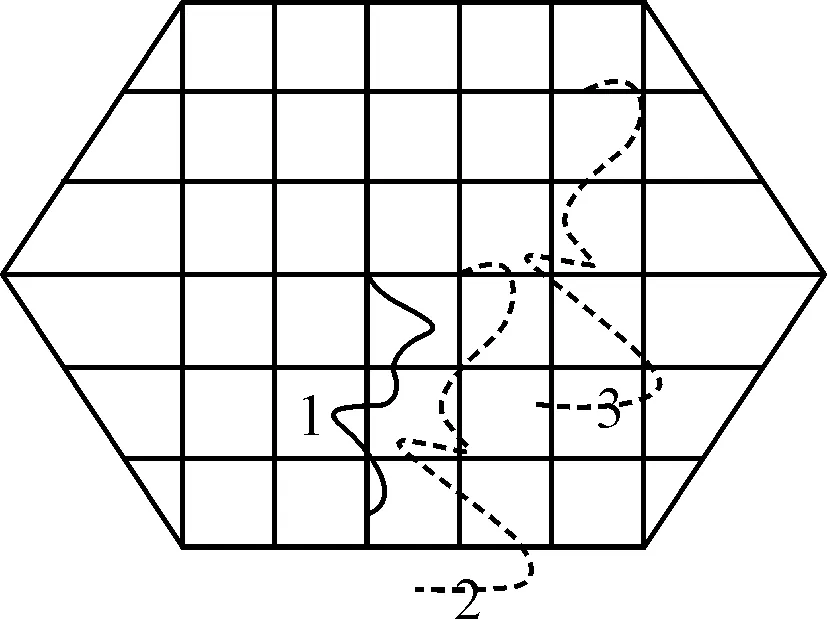
图2 目标模拟示意图
为了解决这一问题,合理做法就是设计方法使得目标运动轨迹如图2中虚线3所示。该方法就是要使得目标在阵列辐射位置相对于轨迹2的起始位置分别旋转高低角β和方位角α,这样,在整个弹道的目标轨迹全部都在阵列辐射信号的范围内,可以实现验证弹道的需求。旋转高低角β和α大小确定的准则是在进行弹道过程中,使得弹体在转台上摆动时,整个弹道的视线角都在阵列辐射信号范围内。该种方法的引入可以有效地改善半实物仿真系统的系能,扩大了阵列式射频仿真试验系统的能力。
本文下述部分将针对天线阵列旋转的高低角和方位角来讨论三轴转台的驱动设置和天线阵列角度设置,使得该方法顺利应用于阵列式射频半实物仿真系统中,提高试验室的验证能力。
3 模拟大视场角方法的实现
3.1 坐标系定义
阵列式射频仿真系统涉及多个坐标系,为了方便描述问题并引入转台发射坐标系,首先介绍常用坐标系统[2]。
1) 惯性坐标系(地面坐标系Axyz):与地球表面固联,原点A常取在导弹发射点;Ax轴指向弹道面与水平面的交线,指向目标为正;Ay轴沿垂线向上,Az轴与其他两轴垂直并构成右手坐标系。
2) 弹体坐标系Ax1y1z1:Ax1轴与弹体纵轴重合,指向头部为正;Ay1轴位于弹体纵向对称面内与Ax1轴垂直,指向上为正;Az1轴垂直于Ax1y1平面,方向按右手直角坐标系确定。
3) 试验室坐标系(转台发射坐标系)Aztxztyztzzt:定义三轴转台的回转中心(天线阵列的球面的球心)为坐标系原点,Aztxzt轴指向阵列的中心点,Aztyzt轴垂直向上,Aztzzt轴由右手法则确定。当转台不旋转时,试验室坐标系与转台三个轴重合,因此试验室坐标系又称转台发射坐标系;当设置初始角度时,转台发射坐标系依次旋转两个角度:即先绕OztYzt轴转动α角,再绕OztZzt轴转动β角,最终形成惯性系Axyz。
4) 目标阵列坐标系:目标的辐射的高低角bet和方位角alfa是由惯性系下的弹目位置关系确定的,其关系为
bet=asin(YO/D)
(1)
alfa=-atan(ZO/XO)
(2)
式中XO,YO,ZO为弹目相对距离在惯性系下的投影,D为弹目相对距离。
各个坐标变换关系如图3所示。

图3 各个坐标系之间的关系
3.2 目标辐射角度确定
由于天线阵列使用的也是转台发射坐标系,设目标在坐标系为旋转之前的辐射坐标为M,对应的惯性系下的直角坐标系的值为(XO,YO,ZO),则对应的角度值为(alfa,bet);如果要旋转的高低角和方位角分别为β和α,则转台发射坐标系依次绕对应的Y、Z轴旋转α和β角度,假设在转台发射坐标系下的目标的直角坐标系值M′为(XOzt,YOzt,ZOzt),则有
(3)
式中,L(α),L(β)分别为坐标系绕Y,Z轴旋转角度常值α,β角的方向余弦值:

(4)

(5)
则目标M′在转台发射坐标系下的目标实际辐射角位置为(alfazt,betzt)为
alfazt=-atan(ZOzt/XOzt)
(6)
betzt=asin(YOzt/D)
(7)
3.3 三轴转台初值设置和驱动方程设计
从图3中各个坐标系间的旋转变换关系可知,已知弹体坐标系相对于惯性坐标系旋转的角度为ψ,θ,γ,惯性系相对于转台发射坐标系旋转的角度为α和β,则在转台发射坐标的任意的单位向量[x,y,z]′,则有
(8)
式(8)中,等式的右边ψ,θ,γ为已知的弹体姿态角,α,β为目标在阵列上旋转的方位角、高低角,等式的左边的ψ2,θ2,γ2为要求的转台发射坐标系转动的角度。则根据式(8)可以得到
(9)
(10)
其中
A12=cos(θ)*cos(ψ)*sin(β)+sin(θ)*cos(β)
A13= -cos(θ)*cos(ψ)*sin(β)*sin(α)
+sin(θ)*sin(β1)*sin(α)
-cos(θ)*sin(ψ)*cos(α)
A11= cos(θ)*cos(ψ)*cos(β)*cos(α)
-sin(θ)*sin(β)*cos(α)
-cos(θ)*sin(ψ)*sin(α)
A32= (sin(θ)*cos(ψ)*sin(γ)+sin(ψ)
*cos(γ))*sin(β)+(-cos(θ)
*sin(γ))*cos(β)
A22= (-sin(θ)*cos(ψ)*cos(γ)+sin(ψ)
*sin(γ))*sin(β)+(cos(θ)
*cos(γ))*cos(α)
可以求得在阵列旋转角度相应的方位角和高低角(α,β)后,转台应执行的初始角度(ψ2,θ2,γ2)。

根据欧拉角旋转的次序和坐标转换关系[2],可以求得弹体角速度和环架旋转角速度的关系如下所示。
(11)

图4 仿真转台环架结构图
则可以求得转台的转动角度为
(12)
即方程(13)
(13)
由式(13)可得转台在整个弹道过程中应执行的转动角速度。
4 仿真试验情况
为了保证在进行半实物仿真试验时,使用本文设计的方案不会改变制导雷达的目标检测信息,也就是不改变导引头在弹体上观察目标的角位置信息。即未旋转前的目标M(在天线阵列角位置(alfa,bet))在弹体姿态角ψ,θ,γ投影下的弹体视线角和旋转后的目标M′(在天线阵列角位置(alfa′,bet′))在弹体姿态角ψ2,θ2,γ2投影的弹体视线角应是相等的。通过验证旋转前后的弹体视线角的变化来验证半实物仿真系统模拟大视场角试验方法的正确性。为了验证上述方法开展了半实物仿真试验。以某型雷达导弹的弹道条件为例,对目标的方位和高低分别旋转-8°和15°,则弹体系下目标角位置对比示意如图5~6所示。

图5 目标在弹体系下的方位角

图6 目标在弹体系下高低角
由图5和图6可知,对目标方位和高低分别旋转-8°和15°,并未改变导引头在弹体上观察目标的角度,由此可见,所设计的方法不会影响导弹末制导对目标检测信息。
而此时,目标阵列的目标辐射信号,方位角从[0 12]变化到[-8 4],高低角从[-18 0]变化到[-4.5 13.5],可以有效地将辐射目标的轨迹从天线阵列的靠下区域移到靠近阵列的中心区域;转台的转动范围也发生变化,导弹偏航角从[0 30]变化到[-8 21],俯仰角从[-18 0]变化到[-5.88 15]。这样可以有效利用目标阵列中心部分的目标模拟能力,防止因为目标视场角过大,出现天线阵列的范围,造成仿真试验无法进行的状况。目标在天线上的方位角和转台的弹体姿态角变化曲线如图7~10所示。
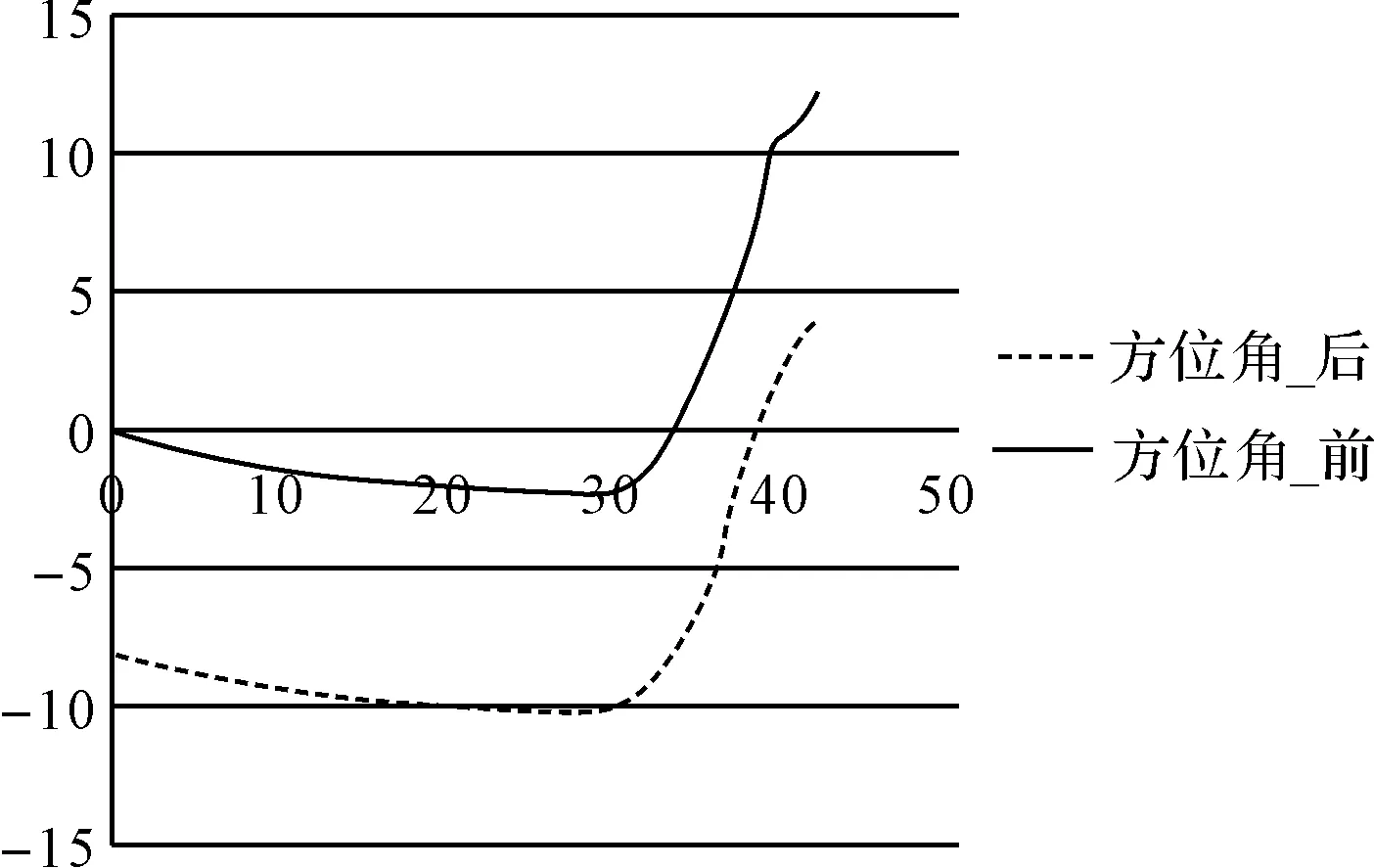
图7 目标在天线阵列上的方位角变化图

图8 目标在天线阵列上的高低角变化图

图9 转台俯仰角变化图
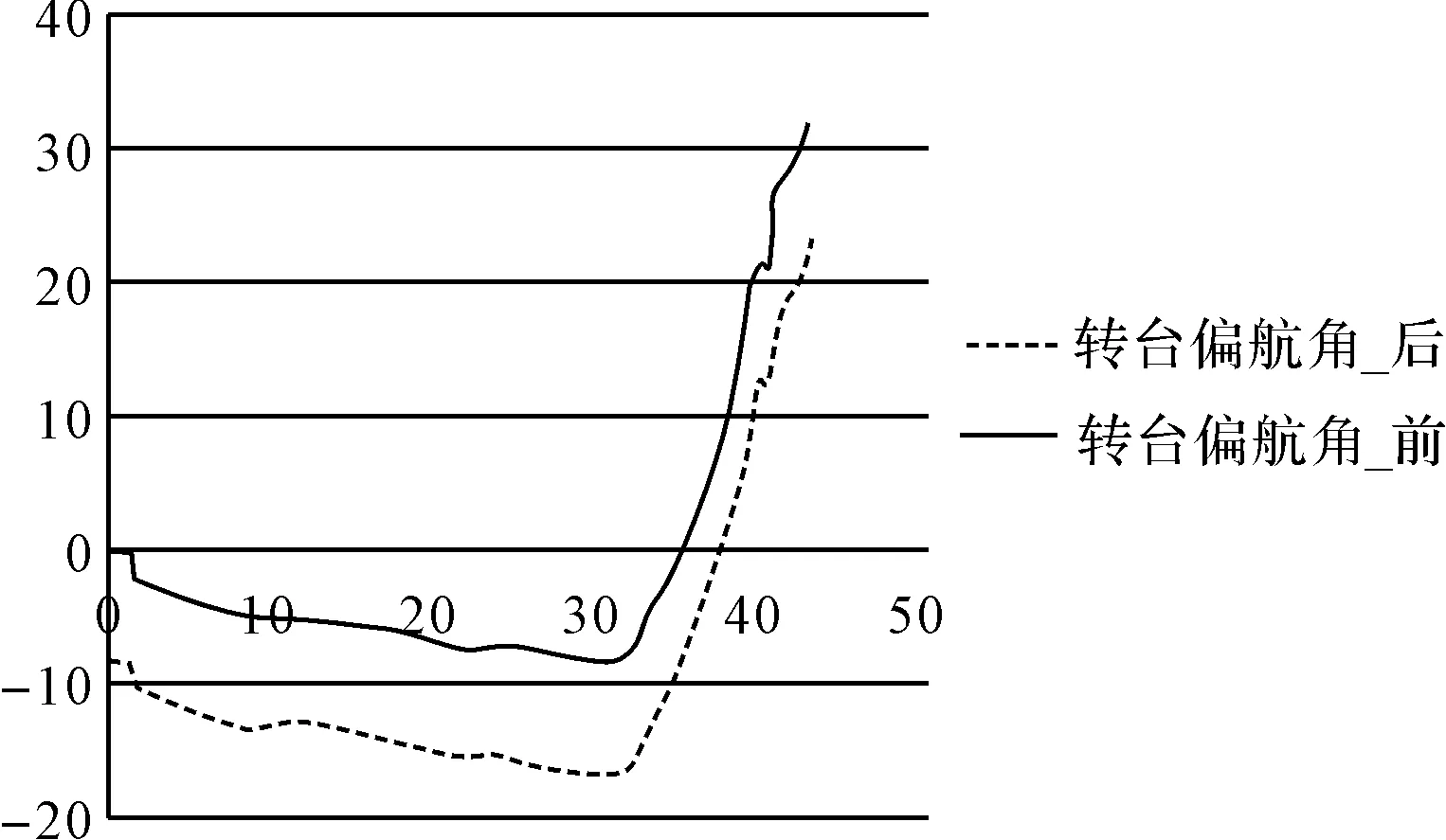
图10 转台偏航角变化图
5 结语
本文针对阵列式射频半实物仿真试验过程中,由于设备空间的局限性,使得某些发射条件无法得到满足的问题,通过分析各个坐标系之间的关系,设计了转台的驱动方法和阵列式天线角度的设置,从而解决目标角度模拟受限等实际问题,扩大了阵列式射频仿真系统的模拟能力,拓展了半实物仿真试验能力。
[1] 梁艳青,崔彬,刘晓宁.阵列式射频目标仿真系统中的目标控制方法[J].航空兵器,2007,2(1):36-39. LIANG Yanqing, CUI Bin, LIU Xiaoning. Target control method in Radio Frequency Target simulation system in antenna Array Pattern[J]. Aero Weaponry,2007,2(1):36-39.
[2] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2006. QIAN Xingfang, LIN Ruixiong. Missile Flight Mechanics[M]. Beijing: Beijing institute of technology press,2006.
[3] 孟秀云.导弹制导与控制原理[M].北京:北京理工大学出版社,2003. MENG Xiuyun. Missile guidance and control principle[M]. Beijing: Beijing institute of technology press,2003.
[4] 梅晓榕,陈明,张卯瑞.三轴仿真转台的建模与仿真[J].系统仿真学报,2001,13(3):278-279. MEI Xiaorong, CHEN Ming, ZHANG Maorui. Mathematical Modeling and Simulation of Three-Axis Flight Motion Simulator[J]. Journal of System Simulation,2001,13(3):278-279.
[5] 宋涛.射频仿真系统中目标阵列的误差分析[D].南京:南京航空航天大学,2008. SONG Tao. Error Analysis of target array in Radio Frequency Simulation System[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2008.
[6] 毛继志,郭陈江,张麟兮.幅相误差对射频仿真系统目标位置精度的影响[J].系统仿真学报,2003,15(8):1149-1151. MAO Jizhi, GUO Chenjiang, ZHANG Linxi. The Influence of Amplitude and Phase Error for Target Positioning Error in RFSS[J]. Journal of System Simulation,2003,15(8):1149-1151.
[7] 赵军仓,樊红社.射频仿真系统中目标的研究[J].陕西理工学院学报,2006,22(2):19-22. ZHAO Juncang, FAN Hongshe. Research on target in radio frequency simulation system[J]. Journal of Shanxi university of Technology,2006,22(2):19-22.
[8] 刘学军,朱根才.一种新的射频仿真目标位置控制办法与软件研究[J].南京航空航天大学学报,2001,33(3):296-299. LIU Xuejun, ZHU Gencai. Target Orientation Handling Method and Program in Radio Frequency Simulation System[J]. Journal of Nanjing University of Aeronautics & Astronautics,2001,33(3):296-299.
[9] 郭晶.三轴转台设计问题研究[D].哈尔滨:哈尔滨工业大学,1995. GUO Jing. Research on the Problem of The three-axis Flight Motion Simulator[D]. Harbin: Harbin Institute of Technology,1995.
[10] 刘春芳,吴盛林.三轴飞行模拟仿真转台的设计及控制问题研究[J].中国惯导技术学报,2003(1):62-65. LIU Chunfang, WU Shenglin. Design and Research on Control Strategy of Three-axis Motion Simulator[J]. Journal of Chinese inertial Technology,2003(1):62-65.
[11] 陆军杰.射频仿真系统误差分析[M].哈尔滨:哈尔滨工程大学出版社,2001. LU Junjie. Error analysis of RF Simulation system[M]. Harbin: Harbin Engineering University Press,2001.
Target Simulation Enrichment Method of Simulation System in Antenna Array Pattern
LIU Zhiyong1,2CHU Jianchuan1,2XU Ke1,2
(1. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Luoyang 471099) (2. China Airborne Missile Academy, Luoyang 471099)
The radio frequency simulation system (RFSS) is an important method to validate the performance of missile, Target simulation is confined to the limit of field viewing angles in process of HIL expermentation. Aimming at solving the problem, the paper introduces the setting of the flight simulation and the anternna array pattern to enrich the target simulation of angles. The simulation results indicate that the method is right.
RFSS, simulation of target angles, setting of the flight simulation
2016年9月14日,
2016年10月21日
刘志永,男,硕士,工程师,研究方向:射频制导与仿真。褚建川,男,硕士,高级工程师,研究方向:射频制导总体设计。许轲,男,高级工程师,研究方向:射频制导仿真设计。
TP311
10.3969/j.issn.1672-9722.2017.03.012
