GRACE重力反演中的轨道数值积分方法分析

余 彪，范东明，游 为，谷延超，苏 勇

(1.西南交通大学地球科学与环境工程学院，成都611756；2.西南石油大学土木工程与建筑学院，成都610500)

GRACE重力反演中的轨道数值积分方法分析

余 彪1，范东明1，游 为1，谷延超1，苏 勇2

(1.西南交通大学地球科学与环境工程学院，成都611756；2.西南石油大学土木工程与建筑学院，成都610500)

首先,对比分析Runge-Kutta积分法、Adams-Cowell联合并行积分法、Gauss-Jackson积分法以及天体力学中常用的外插积分法用于GRACE卫星轨道积分及变分方程解算时的优缺点,得出Gauss-Jackson算法优于其它算法并推荐了相对较优的阶数和步长，从算法的推导过程中分析出了Gauss-Jackson算法优于其它算法的原因。其次,对比不同积分方法抵抗误差的能力，结果表明这些方法都不能有效抵抗误差的干扰；并分析初始状态向量误差和摄动力误差对轨道积分的影响，结果表明,卫星初始状态向量中的速度误差(0.1mm/s)对轨道积分的影响大于位置误差(10mm)对轨道积分的影响，摄动力中的随机误差对轨道积分的影响较大且无规律可循。针对Gauss-Jackson算法中的不足，提出基于移动窗口的多项式内插算法和Gauss-Jackson算法相结合的组合方法(改进Gauss-Jackson算法)，通过模拟和实测数据的计算表明该方法在保证积分精度的前提下不仅提高了积分效率而且可以得到任意时刻的积分值。

轨道积分；积分精度；积分效率；误差影响

0 引 言

在利用重力恢复与气候实验(Gravity recovery and climate experiment, GRACE)卫星数据反演静态或时变地球重力场模型以及下一代重力卫星(如NGGM: Next generation gravity measurements和GRACE-FO:GRACE follow-on)反演重力场的模拟计算中，需要用数值积分方法计算卫星参考轨道和动力学反演方法中的变分方程等。而高精度、高效率和高稳定性的数值积分方法对于地球重力场模型的计算至关重要。

目前,广泛使用的数值积分方法主要有Runge-Kutta积分法(简称RK方法)、Adams-Cowell联合并行积分法(简称AC方法)、Gauss-Jackson积分法(简称GJ方法)、天体力学中常用的外插积分法(简称EX方法)和Collocation积分法(配置法)[1-9]。不同的积分方法优缺点不同[1-2]，单步法(如RK方法)可以自起步积分，但是计算效率较低；多步法(如AC方法，GJ方法)虽然计算效率高于单步法，但是无法自起步；Collocation积分法一般用于受力相对简单的高轨卫星轨道积分，如国际上著名的GNSS定轨定位软件Bernese就是采用这种方法，但低轨GRACE卫星，受力比较复杂，实际计算时并不能很好地模型化卫星受力情况，采用此种方法进行轨道积分时积分精度不如其它方法，所以本文未对其进行对比分析。即使同一种积分方法，采用不同的阶数和步长进行计算时也会得到不同精度的结果。在对卫星进行轨道积分时，卫星初始状态向量及摄动力中含有各种误差，为了得到高精度和高稳定性的积分结果需要分析误差对轨道积分的影响。低轨卫星轨道积分往往效率比较低，而且一般只能得到历元为步长的整数倍处的轨道状态，若采用GPS解算的几何轨道作为标准轨道进行地球重力场模型反演，则可能需要将历元为非步长整数倍处的轨道归算到历元为步长整数倍处的轨道。

因此本文首先从轨道积分精度、积分效率及状态转移矩阵积分精度方面对比分析现有的常用数值积分方法，然后分析了初始状态向量和摄动力误差对轨道积分的影响。针对目前轨道积分算法的不足，基于本文的研究提出了改进GJ算法，该算法采用适当阶数和较大步长的GJ算法，保证积分精度并结合基于移动窗口的多项式内插算法计算出步长范围内任意历元处的轨道。由于采用了较大的积分步长，使得积分效率相比于采用5s步长的积分效率成倍增加，而积分精度并不会降低；由于采用了基于移动窗口的多项式内插算法可以内插出任意时刻的积分轨道，降低了不规则历元处轨道处理的难度。

1 数值积分方法

RK方法是最常用的单步积分法且存在多种不同算法[1]，即便是同一阶方法也存在不同的算法且算法之间计算精度相差较大，本文采用轨道积分精度较高的8阶RK算法[5-6,8-9]，8阶RK积分方法每积分一步都需计算10次右函数，对于GRACE卫星实际观测数据，计算一次右函数(主要指卫星所受的所有摄动力)大约需要耗时0.1s(在配有Intel Core四核处理器，主频为2.50GHz的PC机上采用Fortran语言计算)，这对于实际轨道积分计算效率低下。

EX积分法是单步积分法[1,4]，其计算过程分为两步，首先以不同步长计算某一历元处的近似值然后对近似值外插逐渐逼近轨道真值。通过计算发现,对于GRACE卫星轨道，三角EX法[1]比菱形EX法[4]具有更高的数值稳定性，所以本文采用三角EX算法。

AC方法为多步积分法，计算效率高于单步法，为了提高计算精度，本文在计算中结合预估校正迭代算法[1-3,5]，并与单步法的计算效率进行对比，本文在计算中采用8阶RK方法提供初值。

GJ算法也为多步积分法，为了起到更好的对比效果，GJ方法起步值的计算并未采用文献[3]和[10]中介绍的Mid-Corrector公式，而采用与AC方法相同的起步算法(8阶RK方法)，计算中同样结合预估校正迭代算法。

2 不同方法轨道和状态转移矩阵积分对比

通过比较不同方法的轨道和状态转移矩阵积分精度，得出最优方法；比较同一方法不同阶数和步长的计算结果得出计算精度较高的阶数和步长范围。目前GRACE重力反演是分弧段进行处理的，弧段长度一般定为一天，但卫星绕地球运行时受地球引力的作用是连续累积的，从理论上说采用连续的弧段而不进行分弧段处理有益于地球重力场的反演；并且由于目前GRACE时变地球重力场模型的时间尺度一般为一个月，本文在积分时直接采用一个月作为积分的时间跨度。

为了得到轨道的解析解，考虑卫星只受地球中心引力的二体问题。根据开普勒轨道理论计算卫星轨道解析解，将不同积分方法以不同的阶数和步长计算积分轨道并与开普勒轨道比较得到积分误差。采用表1中的GRACE卫星轨道参数作为初始历元的开普勒轨道根数，并以不同步长计算得到一个月的开普勒轨道。

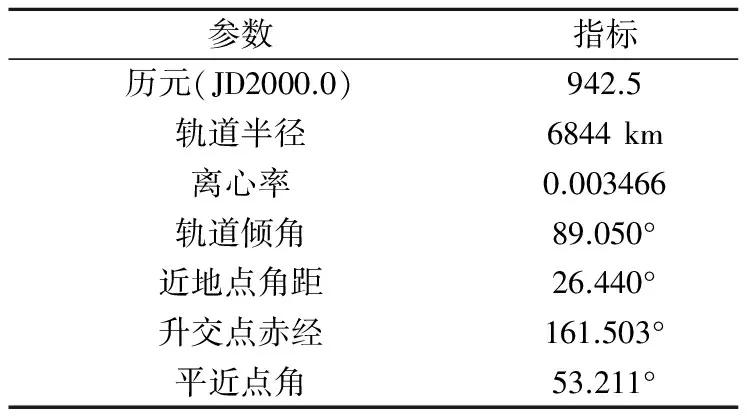
表1 GRACE卫星初始轨道根数

2.1 卫星轨道积分误差对比

对于EX方法，外插计算一次算法阶数增加2[1]，所以该方法只有偶数阶。当选取的阶数很高时，积分轨道仍收敛，但是该算法的积分效率会随着阶数的增加迅速降低(第2.2节详细说明)，考虑到实际计算效率本文只分析前20阶的计算精度。图1(b)表示不同阶数和步长的EX方法积分轨道误差。

对于AC方法，满足积分精度要求的阶数为8阶到13阶。图1(c)表示不同阶数和步长的AC方法积分轨道误差。从图1(c)可以看出，该方法在步长小于15s时，采用任何一种阶数进行积分都无法满足mm级的误差要求(如常用的12阶5s步长积分一个月的最大误差为40.4mm)。

对于GJ方法，满足积分精度要求的阶数为3阶到12阶。图1(d)表示不同阶数和步长的GJ方法积分轨道误差。从图1(d)可以看出，GJ方法积分误差普遍比上述几种方法小(可达两个量级)，而且该方法3到12阶5s步长的积分误差皆满足要求。

对比分析图1的结果可以得出以下两点结论：1)对于卫星轨道积分并不是积分步长越短越好、积分阶数越高越好。其可能的原因为，当积分步长较小时，积分计算的历元个数增多，则轨道积分累计误差或计算机的累计舍入误差会增大；当积分步长较大时，用于内插右函数值的弧段较长，则内插出的右函数值与实际右函数值的差值较大[11]，从而影响轨道积分的精度。当积分的阶数较大时，积分下一个历元时所用到的前面历元的个数增多，则用于内插右函数的弧段增长，内插出的右函数误差可能增大[11]；而当阶数较小时，则用于内插右函数的多项式的阶数小，右函数的插值余项变大[11]，即右函数的近似误差大。所以积分步长和积分阶数应根据精度、效率和观测数据采样要求合理选择。2)从不同方法轨道积分误差角度看，GJ方法优于其它方法。通过对比分析各积分算法的推导过程，以GJ算法和AC算法为例来说明GJ算法优于其它算法的原因。GJ算法与AC算法同为多步法，而且公式推导过程相似。两套算法都是基于基本数学物理公式：

(1)

(2)

之前可认为都是一样的。AC算法将式(2)化为：

(3)

GJ算法将式(2)转化为：

(rn+1-rn)-(rn-rn-1)=▽2rn+1=

(4)

2.2 卫星轨道积分效率对比

在卫星轨道积分时，除了要考虑积分误差，还应该考虑积分效率，影响轨道积分效率的主要因素是右函数的计算次数。一般情况下，单步法的计算效率低于多步法，但为了提高多步法的计算精度，常常结合预估校正迭代算法，本节主要比较结合预估校正迭代算法的多步法和单步法的计算效率。

对于8阶RK方法，积分一步大约需要花费1s的时间。图2(a)反应了不同步长8阶RK方法计算一个月的积分轨道时右函数计算次数。

对于EX方法，该方法需要以不同的步长计算某一历元处卫星的状态得到EX方法的初值，在计算初值的过程中需要多次计算右函数。图2(b)反应的是不同步长和阶数的EX方法计算一个月的积分轨道时右函数计算次数。从图2(b)可以看出，EX方法右函数的计算次数会随着阶数的增高成倍的增加，而且相比于同阶的RK方法，EX方法右函数的计算次数明显要更多。

对于AC联合并行预估校正迭代算法，虽然需要进行迭代计算，但在对GRACE卫星轨道的积分计算中发现不需要迭代几次即可满足精度要求，所以并不会增加多少额外的计算时间。图2(c)反应的是不同步长的偶数阶AC方法计算一个月的积分轨道时右函数的计算次数。通过与图2(a)和图2(b)对比发现,该方法的右函数计算次数明显少于RK方法和EX方法。

对于GJ方法，采用同样的积分策略得到图2(d)。从图中可以看出，GJ方法也不需要迭代几次就可满足精度要求，且阶数越高计算效率相对越高。对比图2(c)与图2(d)可知，AC方法与GJ方法的计算次数几乎相等，且都小于RK方法和EX方法。

通过分析比较不同方法用于GRACE卫星轨道积分时右函数计算次数，可以得出EX方法计算时右函数计算次数最多，所以积分效率最低，其次为RK方法，AC方法和GJ方法。

2.3 状态转移矩阵积分误差对比

在用动力学法反演地球重力场模型时需要计算状态转移矩阵和参数敏感矩阵，一般通过对变分方程进行数值积分实现[1,5-6]。积分过程中，首先要积分每个历元处卫星的状态向量，再由卫星状态向量计算状态转移矩阵或参数敏感矩阵的导数(右函数)，最后由右函数计算下一历元的状态转移矩阵或参数敏感矩阵。对于二体问题，可通过解析法得到状态转移矩阵，文献[12]提供了二体问题状态转移矩阵解析解算法。本文在二体问题下比较不同方法用于状态转移矩阵积分时的积分误差，仍然采用表1中的GRACE卫星轨道参数作为初始历元的开普勒轨道根数。由于在积分状态转移矩阵时需要积卫星轨道，EX方法积分卫星轨道效率低下，所以此处并未对EX方法进行比较。状态转移矩阵积分效率主要受轨道积分的影响，所以轨道积分效率高的方法状态转移矩阵积分同样效率高。表2为不同方法积分一个月的状态转移矩阵误差(状态转移矩阵36个元素中积分误差最大值)，表中符号*表示积分发散。从表2可以看出,GJ方法积分状态转移矩阵误差比AC方法小一个量级，与RK积分方法的积分误差相当。

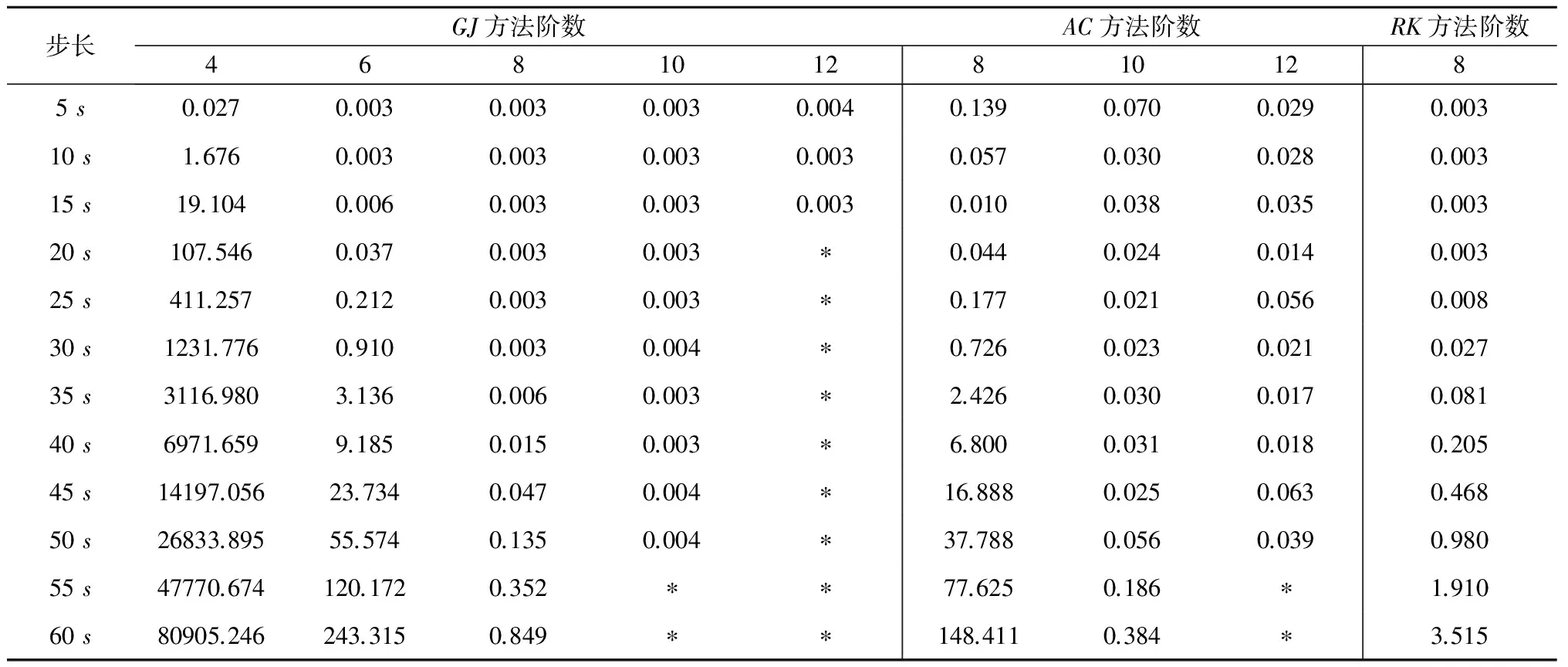
表2 不同参数下的各种方法状态转移矩阵积分误差最大值

基于第2.1～2.3节的分析考虑到GJ算法用于GRACE卫星轨道和状态转移矩阵积分相对于其它三种积分方法有较大优势，表3给出了GJ算法积分误差相对较小的阶数以及对应的步长，其它三种积分方法不推荐用于长弧段的GRACE卫星轨道及状态转移矩阵积分。

表3 GJ算法相对较优阶数及对应步长

3 误差对轨道积分影响分析

由于轨道积分需要初始时刻的卫星状态向量，而从GRACELevel1B的GNV1B文件或其它轨道文件中获得的数据含有误差，该误差会影响积分轨道的计算。除了初始时刻的卫星状态含有误差之外，积分计算时摄动力中含有的误差也会对积分轨道产生影响。

3.1 初始状态误差对轨道积分的影响

为了分析卫星初始时刻状态向量误差对轨道积分的影响，在轨道积分时分别仅对初始状态向量中的位置和速度向量加入不同量级的误差，分析该误差对轨道积分的影响。通过采用不同的积分方法积分后发现初始状态误差对不同积分方法的影响几乎相同，因此本文以GJ方法为例分析初始状态误差对轨道积分的影响。图3(a)为仅对初始时刻卫星位置向量加入不同量级误差(100mm级误差表示X、Y、Z方向各加100mm误差，其它情形类似)后积分轨道误差图。图3(b)为仅对卫星初始时刻速度向量加入不同量级误差(mm/s级误差表示X、Y、Z方向各加1mm/s误差，其它情形类似)后积分轨道误差图。为了分析初始状态中位置和速度向量误差对积分轨道的综合影响，在初始状态中共同加入不同量级的位置和速度误差后得到积分轨道误差图3(c)。

通过比较分析图3的计算结果可以得出以下结论：初始状态误差对积分轨道的影响为随着积分时间增加积分轨道误差呈现线性累加特性。卫星初始状态误差对轨道积分的影响远远大于积分算法本身的误差。对比图3(a)、3(b)和3(c)发现，卫星初始位置和速度向量中速度向量误差(0.1mm/s)对轨道积分的影响大于位置向量误差(10mm)对轨道积分的影响，若位置误差为10mm量级，则当速度误差为0.01mm/s量级时，两者对轨道积分的影响才能保持一致，而在当前卫星定轨精度下是很难达到的。其可能的原因为，轨道积分时速度为位置的右函数，而速度的右函数为卫星所受的力。位置误差所引起的摄动力变化相对较小，从而引起的速度变化也相对较小，所以在随后的积分中位置误差相对较小；而如果初始状态中速度存在误差，由于速度为位置的右函数则在对位置进行数值积分时受该速度误差影响较大，会使位置产生相对较大的偏差，具有较大偏差的位置对应的摄动力偏差也相对较大，则在随后的积分中位置误差较大。

3.2 摄动力中的随机误差对轨道积分的影响

在对卫星进行轨道积分时，由于先验力模型及非保守力测量数据的不准确会对轨道积分产生较大的影响。非保守力数据的误差大致为10-10ms-2量级，保守力中主要是先验重力场模型的误差较大，虽然在重力反演中会对先验重力场模型和非保守力数据进行校正，但如果误差较大会影响参数的估计，本文取两个不同的先验重力场模型并取至不同的阶次得到先验重力场模型误差引起的卫星引力误差量级。通过分别计算GGM05C模型(取至140阶次)和EGM2008模型(取至70阶次)对卫星的引力并对引力的差做统计(时间为1d，间隔为5s)得到图4(a)。根据图4(a)的结果在二体问题下，对中心引力加上一个服从正态分布N(0, (5×10-7ms-2)2)的随机误差，图4(b)为以GJ方法计算100次摄动力误差对轨道积分结果影响图。从图4(b)可以看出，摄动力误差对轨道积分的影响可超过20000m,大于初始状态误差对轨道积分的影响且无规律可循，影响也是随机的。基于本文的分析得出若直接采用1个月作为积分弧段进行重力反演，则必须考虑如何减小该误差的影响。

4 改进Gauss-Jackson方法

虽然GJ算法具有较高的计算精度且有多种阶数和步长可以选择，但是该算法只能计算出历元为步长整数倍处的积分轨道。由于GRACE LEVEL1B数据中给出的是5s间隔的标准轨道和星间距观测数据，所以一般采用5s步长进行轨道积分，对于长弧段轨道积分积分效率较低。基于前文的分析得出采用较大的步长进行积分也可以达到较高的积分精度，而且提高了积分效率。为了得到步长内任意点的积分轨道可采用适当的内插算法[13]，只要步长的大小控制在一定的范围内，并选择合适的内插算法，内插的精度可以很高。内插计算不仅可以得到5s步长整数倍处的轨道值，而且可以得到任意历元处的轨道值，当以GPS解算的几何轨道作为标准轨道时可简化几何轨道的预处理。

本文选择8阶30s作为积分阶数和步长，在内插算法上，采用10点9阶基于移动窗口的多项式内插算法[6,14]，在起始段和末尾段采用同阶拉格朗日算法[11]，除了弧段两端外，其它区域能保证为内插窗口的中心区域。通过模拟数据计算得到该种内插算法内插出的轨道误差在10-8～10-9m量级，起始段和末尾段内插出的轨道误差为10-6～10-7m量级，状态转移矩阵误差在10-11量级，完全能满足轨道积分和状态转移矩阵积分要求。内插算法的计算时间相对于右函数的计算时间几乎可以忽略不计，所以改进GJ算法不仅保证了轨道积分精度，而且提高了轨道积分效率。图5为二体问题下采用改进GJ方法计算的积分轨道误差图，完全能满足GRACE卫星积分精度要求。

为了分析改进GJ方法在实际卫星轨道积分中的性能，本文以GRACE Level1B数据以及相应的力模型(见表4)进行轨道积分试验。计算时分别采用8阶5s步长的GJ方法和改进GJ方法进行积分，并从积分精度和积分效率方面进行比较。由于真实数据中存在数据间断和粗差，需要对间断数据进行填充并剔除粗差。为了计算方便，此处利用一天的实际数据进行轨道积分(未对初始状态向量和力模型参数校正)并与JPL提供的轨道数据(GRACE GNV1B)对比。

对比发现，改进GJ方法的最大积分误差比8阶5s步长GJ方法略小(200mm左右)，并在计算效率上有了较大提高。采用8阶5s步长GJ方法用时约57min，采用改进GJ方法用时约18min，积分效率提高了将近3倍。

表4 轨道积分计算所用的力模型

5 结 论

本文对比了多种轨道积分方法并分析了积分起始数据误差对轨道积分结果的影响，提出了改进GJ算法。基于对比分析得出了以下有益的结论：

1)对于GRACE卫星长弧段轨道积分，GJ算法由于在积分的过程中没有直接采用前面历元的积分轨道值使得其积分误差比RK、EX和AC算法小(可达2个量级)。

2)EX算法在积分阶数很高的情况下仍可以保持较高的积分精度，但是对于低轨卫星计算效率低下；AC算法和GJ算法同为多步法，但对于GRACE卫星轨道积分AC算法不及GJ算法，不推荐在长弧段轨道积分中使用EX算法和AC算法，RK算法只建议用于多步法的起步值计算。

3)对于GRACE卫星轨道和状态转移矩阵积分，GJ算法较适宜的积分阶数为8～10阶，对应的步长为5～40s和5～50s。

4)卫星初始状态误差和力模型误差对轨道积分的影响远大于算法本身的误差；初始状态中的速度误差(0.1mm/s)对轨道积分的影响比位置误差(10mm)大将近1个量级，且该类误差对轨道积分的影响呈现线性累加特性；力模型误差对轨道积分的影响较大且无规律可循。

5)GJ算法中取合适的较大积分步长(30s)并结合适宜阶数(9阶)的基于移动窗口的多项式内插算法不仅可以大大提高积分效率而且可以得到任意时刻卫星的积分轨道和状态转移矩阵，有利于GRACE卫星不规则历元的几何轨道和星间观测值联合进行卫星重力反演。

[1] Montenbruck O, Gill E. Satellite orbits: models, methods, and applications[M]. Berlin: Springer-Verlag, 2005.

[2] Beutler G. Methods of celestial mechanics[M]. Berlin: Springer-Verlag, 2005.

[3] Berry M M, Healy L M. Implementation of Gauss-Jackson integration for orbit propagation [J]. The Journal of the Astronautical Sciences, 2004, 52(3): 331-357.

[4] Bulirsch R, Stoer J. Numerical treatment of ordinary differential equations by extrapolation methods [J].Numerische Mathematik, 1966, 8(1): 1-13.

[5] 王正涛. 卫星跟踪卫星测量确定地球重力场的理论与方法[D]. 武汉: 武汉大学, 2005.[Wang Zheng-tao. Theory and methodology of earth gravity field recovery by satellite-to-satellite tracking data[D]. Wuhan: Wuhan University, 2005.]

[6] 游为. 应用低轨卫星数据反演地球重力场模型的理论和方法[D]. 成都: 西南交通大学, 2011. [You Wei. Theory and methodology of earth′s gravitational field model recovery by LEO data[D]. Chengdu: Southwest Jiaotong University, 2011.]

[7] 龚晓颖, 蔡诗响, 李征航. 小步长低阶Collocation方法轨道积分性能研究[J]. 宇航学报,2013, 34(5): 642-648. [Gong Xiao-ying, Cai Shi-xiang, Li Zheng-hang. Performance research of small-step length and low-order collocation method in orbit determination[J]. Journal of Astronautics, 2013, 34(5): 642-648.]

[8] Xu G C. GPS theory, algorithms and applications[M]. Berlin: Springer-Verlag, 2007.

[9] 刘大杰, 施一民, 过静珺.全球定位系统(GPS)的理论与数据处理[M]. 上海: 同济大学出版社, 1997: 257-263.

[10] 罗志才,周浩, 钟波, 等. Gauss-Jackson积分算法分析与验证[J]. 武汉大学学报·信息科学版, 2013, 38(11)：1364-1368.[Luo Zhi-cai, Zhou Hao, Zhong Bo, et al. Analysis and validation of Gauss-Jackson integral algorithm[J]. Geomatics and Information Science of Wuhan University, 2013, 38(11): 1364-1368.]

[11] 李大美, 李素贞, 朱方生. 计算方法[M]. 武汉: 武汉大学出版社, 2012: 94-130.

[12] 蒋虎, 黄珹, 胡小工. 二体问题状态转移矩阵的分析解和数值解比较[J]. 云南天文台台刊,1999, 4: 19-29. [Jiang Hu, Huang Cheng, Hu Xiao-gong. Comparison between analytic and numerical solutions of state transition matrices of two body problem[J]. Publications of the Yunnan Astronomical Observatory, 1999, 4: 19-29 .]

[13] 郑伟, 许厚泽, 钟敏, 等. 不同插值法对下一代卫星重力反演精度的影响[J]. 宇航学报, 2014, 35(3): 269-276. [Zheng Wei, Xu Hou-ze, Zhong Min, et al. Influences of different interpolation methods on accuracy of next-generation satellite gravity recovery[J]. Journal of Astronautics, 2014, 35(3): 269-276.]

[14] 游为, 沈云中, 范东明, 等. 基于卫星轨道扰动理论的重力反演方法[J]. 地球物理学报, 2010, 53(11): 2574-2581. [You Wei, Shen Yun-zhong, Fan Dong-ming, et al. The algorithm of earth′s gravitational field recovery based on satellite′s orbital perturbation theory[J]. Chinese Journal of Geophysics, 2010, 53(11): 2574-2581.]

通信地址：四川省成都市郫都区西南交通大学地球科学与环境工程学院(611756)

电话：18382157390

E-mail:yubiao0221@qq.com

游 为(1985-)，男，讲师，博士，主要从事卫星重力测量及测量数据处理研究。本文通信作者。

通信地址：四川省成都市郫都区西南交通大学地球科学与环境工程学院(611756)

电话：18123216821

E-mail: youwei1985@foxmail.com

(编辑：牛苗苗)

Analysis of Orbit Numerical Integration Methods in Earth′s Gravitational Field Recovery by GRACE

YU Biao1, FAN Dong-ming1, YOU Wei1, GU Yan-chao1, SU Yong2

(1.Faculty of Geosciences and Environmental Engineering, Southwest Jiao-tong University, Chengdu 611756, China; 2.School of Civil Engineering and Architecture, Southwest Petroleum University, Chengdu 610500, China)

This paper assesses the existing numerical integration methods including the Runge-Kutta methods, the Adams-Cowell methods, the Gauss-Jackson methods and the extrapolation methods in the computation of the GRACE satellite orbits and state transition matrix. According to the results, we recommend the Gauss-Jackson methods with optimal parameters to integral orbit and also analyze the advantages of the Gauss-Jackson methods relative to the other methods. Then the resistance capacity of the random errors which are included in the satellite initial state for those methods is analyzed, and the numerical results indicate that all methods show the similar little resistance capacity. The integral orbits are more sensitive to the satellite initial state velocity errors (0.1mm/s) than the initial state position errors(10mm). Compared to the errors in the satellite initial state, the perturbation force model errors have a significant impact on the orbit integral precision. Finally, we proposes a modified method which combines the Gauss-Jackson algorithm and the moving-window polynomial interpolation algorithm to overcome the shortage of the large step size of the Gauss-Jackson method. The simulated and actual results show that the modified method can give the satellite position and state transition matrix at any time and has a significant improvement in computing efficiency while possessing high accuracy.

Orbit integration; Integral precision; Integral efficiency; Error influence

2016-10-24;

2017-01-03

国家自然科学基金(41574018,41404018)

P228.1

A

1000-1328(2017)03-0253-09

10.3873/j.issn.1000-1328.2017.03.005

余 彪(1990-)，男，硕士生，主要从事卫星重力测量研究。