新型高超声速飞行器耦合姿态控制系统设计

郭宗易，周 军，郭建国

(西北工业大学精确制导与控制研究所，西安710072)

新型高超声速飞行器耦合姿态控制系统设计

郭宗易，周 军，郭建国

(西北工业大学精确制导与控制研究所，西安710072)

针对具有强耦合和强不确定性特点的高超声速飞行器控制问题，提出一种考虑耦合特性的新型鲁棒姿态控制律。首先，建立高超声速飞行器的姿态动力学方程，并基于反步法思想转化为误差动态模型；然后结合干扰观测器提出基于耦合特性的飞行器鲁棒控制方法，并设计滑模补偿项保证姿态角渐近收敛到跟踪指令；最后基于绝对误差积分(IAE)指标从理论上证明本文方法相对于未考虑耦合特性的方法具有更好的动态性能。本文提出的控制方法不仅保证系统渐近稳定性和强鲁棒性，而且将耦合特性考虑进控制器设计中，进而提升了系统的动态性能。数值仿真考虑气动参数拉偏以及实际的执行机构幅值和速率限制，仿真结果校验了本文控制系统设计的有效性。

高超声速飞行器；耦合特性；干扰观测器；滑模补偿项；绝对误差积分(IAE)

0 引 言

高超声速飞行器以其快速响应能力、高突防能力和军事战略意义成为近些年各国的研究热点[1]。高超声速飞行器的高速、高空域飞行特点，导致其存在强不确定性、强非线性和强耦合等控制难题，尤其耦合问题目前仍是亟待研究和解决的关键。

解决耦合问题的思路之一是进行解耦控制。由于飞行器模型的复杂性，常规的线性解耦方法已经难以应用到飞行器控制器设计中，所以近些年常用的方法主要是微分几何动态逆控制策略，其基本思想是利用微分几何方法实现系统的精确反馈线性化，实现解耦目的，再结合各种方法设计动态逆控制器。文献[2]针对再入飞行器进行反馈线性化，得到其解耦模型，然后设计滑模干扰观测器对不确定性进行估计和补偿；文献[3]利用动态逆与μ综合结合的方法设计飞行器纵向通道鲁棒控制器；文献[4]采用反馈线性化得到解耦模型，然后基于H∞方法设计控制器。然而，动态逆对模型精确度十分敏感，飞行器的非线性动态特性非常复杂，难以建立精确的数学模型，设计的控制器鲁棒性也较差。

另一种处理耦合的思路是在设计控制器时考虑耦合因素。文献[5]模型中考虑了飞行器姿态模型的通道耦合，在进行解耦后定义残余耦合量，将之考虑进系统的不确定性并采用变结构控制保证系统稳定；文献[6]将高超声速飞行器耦合系统表示成具有非匹配不确定性的关联大系统形式，基于广义关联大系统Lyapunov稳定理论及Riccati方程设计变结构控制方法；文献[7]建立考虑控制通道间耦合因素的制导与控制一体化设计模型，设计非光滑扩张状态观测器进行观测补偿，然后结合块动态逆方法设计保证系统的全局有限时间稳定；文献[8]针对飞行器耦合系统，采用反步法保证系统状态的一致最终有界。此类方法本质上是将耦合视之为不确定性，通过鲁棒控制方法(比如变结构控制)或者扰动估计补偿方法(比如扩张状态观测器)进行处理，缺乏对系统耦合特性的详细分析。目前对于系统耦合对系统性能影响的研究较少，也没有在高超声速飞行器控制中的应用。文献[9]首次在理论上提出基于能量指标的耦合利弊评价方法，并分析耦合对系统性能的影响，但其仅基于传递函数形式，缺乏对常用状态空间形式的分析。

针对以上问题，本文针对高超声速飞行器姿态控制系统，提出一种新型的基于耦合特性的鲁棒控制方法(Coupling-based control, CBC)，并结合干扰观测器和滑模补偿项保证其渐近收敛。本文与其他文献研究的区别在于：1)提出基于耦合特性的飞行器姿态闭环控制器，控制器中反映了耦合对系统性能的影响；2)针对干扰观测器估计不准导致跟踪存在误差的问题，结合鲁棒补偿项实现系统渐近收敛；3)基于绝对误差积分指标(Integral absolute error，IAE)，从理论上证明本文提出的控制方法相对于未考虑耦合特性的控制具有更好的动态性能。

1 飞行器数学模型

1.1 高超声速飞行器姿态系统模型

飞行器姿态系统模型如下所示：

(1)

式中：α、β和γV分别是攻角、侧滑角和倾侧角，ωx、ωy和ωz分别是滚转、偏航和俯仰角速度，θ为速度倾角，L和N代表升力和侧向力，V是飞行器速度，g是重力加速度。Δα、Δβ和ΔγV表达式为：

(2)

式中：ψV为航迹偏航角，φ是飞行器纬度，R为飞行器相对地心的距离。由于实际中存在R>>V，所以一般在模型简化处理中可以将Δα、Δβ和ΔγV考虑到不确定性中。另外，关于坐标系定义、飞行器模型中各量的详细定义和方程推导过程，本文不再赘述，具体请参考文献[8]。

下面给出飞行器的绕质心动力学方程。考虑飞行器为面对称，绕质心动力学方程可以写为

(3)

式中：Mx、My和Mz是飞行器受到的气动力矩，Jx、Jy和Jz分别是飞行器相对机体坐标系三轴的转动惯量。

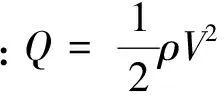
(4)

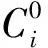
令ξ=[α,β,γV]T,ω= [ωz,ωy,ωx]T，u=[δz,δy,δx]T, 那么将式(4)代入式(1)和式(3)经过简化可得如下高超声速飞行器姿态系统模型

(5)

式中：DF和DM代表飞行器受到的集总不确定性，包括未建模动态、气动系数不确定性和外界扰动等。各系数矩阵的表达式见式(7)，而gξ表达式为

(6)

(7)

控制目标是使得α、β和γV跟踪参考指令αc、βc和γVc。

对于飞行器模型，可以认为ω+gξ项是ξ系统的耦合项，其中ω代表姿态角速度对各通道角度的状态耦合，而gξ代表通道耦合项，反映了各个通道之间的交联影响。在角速度动力学方程中，Aωξξ项是ω系统的耦合项，Aωξξ代表姿态角对各自通道的角速度的状态耦合。模型(5)中Aωω(ω)项包含的交叉耦合项是复杂的非线性耦合，为了简便将之视为已知项，所以本文主要考虑状态耦合和各通道耦合影响。

接下来，需要把式(5)转化为误差系统。指令ξc=[αc,βc,γVc]T，设误差状态eξ=ξ-ξc，对其求导有

(8)

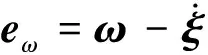
(9)

进一步对eω求导可得

(10)

(11)

如果控制器使得eξ→0，那么有[α,β,γV]T→ [αc,βc,γVc]T。下面，针对误差模型(11)，本文提出一种基于耦合特性的新型鲁棒控制器。

2 控制系统设计

高超声速飞行器的快速响应特点和受到各种不确定性影响的特性，要求设计的控制系统不仅达到良好的动态性能，而且能够具有抵抗不确定性的强鲁棒性。为了满足这种要求，本部分首先引入一种干扰观测器设计方法；然后结合干扰观测器提出考虑耦合特性的鲁棒控制器，并证明系统的有界稳定；最后结合滑模补偿器实现了整个系统的渐近稳定。

2.1 干扰观测器设计

令x=[ξT,ωT]T，那么系统(5)变为如下形式

(12)

其中：

(13)

受文献[11]启发，本文提出新型干扰观测器：

(14)

式中：z∈R6×1是观测器状态，σ0和σ1是观测器增益，其中矩阵Λ∈R6×6是待设计矩阵。

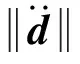
引理 1. 针对系统(12)设计如式(14)的干扰观测器，如果满足假设1，而且σ0=2Λ,σ1=Λ2，矩阵Λ取为Λ=diag(λ,λ,λ,λ,λ,λ)，其中λ> 0，那么干扰的估计误差满足

(15)

式中：r=μ/λ2。

(16)

(17)

下面参考文献[11]中引理1的求解方法可得结论(15)。

2.2 基于耦合特性的鲁棒控制

定理 1. 考虑姿态误差系统(11)，设计如下的控制器

(18)

(19)

式中：(∘)表示Hadamard乘积，函数sgn(x) = [sgn(x1), sgn(x2), …, sgn(xn)]T(x=[x1,x2, …,xn]T)。Jξ1= [Jξ11,Jξ12,Jξ13]T,Jξ2= [Jξ21,Jξ22,Jξ23]T和Jω= [Jω1,Jω2,Jω3]T均是3×1矩阵。而Θ函数定义为

Θ(J)=diag(sgn(J1),sgn(J2),…,sgn(Jn))

(20)

式中：矩阵J=[J1J2…Jn]T。那么姿态系统(11)的跟踪误差渐近稳定到原点附近邻域内。

证. 将控制器(18)代入系统(11)得到闭环系统

(21)

(22)

容易证明不论eξieωi正负，必然有

(23)

1.形象思维和抽象思维的统一符合儿童思维和认知发展特点。儿童主要以形象思维来观察世界。情境教学抓住儿童的这一思维特点，将“形真、情切、意远、理寓其中”融为一个整体，一以贯之，将知识从具体到抽象，再从抽象到具体，让儿童真正理解，这符合儿童思维和认知的发展特点。[1]

(24)

(25)

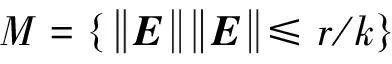
注1. 控制器中的Θ函数即考虑耦合特性的控制器附加项。如果符号函数判断为-1，控制律中将耦合进行抵消；符号函数判断为1，则对耦合加强，最终保证耦合始终对系统性能有利。

注2. 耦合特性量Jξ1、Jξ2和Jω是定义在误差状态基础上的，所以耦合特性是在时刻变化的。这和经典的耦合评价方法相比在本质上是不同的。耦合评价大多针对开环系统耦合评估，但本文提出的耦合特性量可以设计闭环控制器。

注3. 值得注意的是，本文提出的控制器中存在切换项，所以稳定性要在Filippov意义[13]下理解。

2.3 补偿器设计

定理 2. 考虑如式(11)的误差姿态系统，设计如下的控制器

(26)

证. 仍取Lyapunov函数V，将控制器(26)代入系统(11)，对V求导并变换可得

(27)

3 基于绝对误差积分的性能分析

绝对误差积分指标是控制系统中一种常用的性能分析指标[12]：

(28)

式中：e代表系统的跟踪误差。IAE指标能够综合反映出系统跟踪控制的动态特性。下面将基于此指标分析本文方法的优点。针对系统(11)，不考虑耦合特性的常规控制器(Non-coupling-based control, NCBC)为如下形式

u′=B-1(-Kωeω-eξ-Aωω(ω)-Aωξeξ-h+

(29)

定理 3. 不考虑耦合特性的控制器(29)的系统绝对误差积分指标为ΦIAE1，而采用基于耦合特性控制器(26)的指标为ΦIAE2，那么有ΦIAE2≤ΦIAE1。

证. 将控制器(29)代入系统(11)得到闭环系统

(30)

根据式(30)并结合定义(28)计算ΦIAE1，将式(26)代入式(11)，并结合定义(28)可计算ΦIAE2，分别如下所示

(31)

ΦIAE2-ΦIAE1=

(32)

注意到

(33)

将式(33)代入式(32)可得ΦIAE2-ΦIAE1≤ 0。证毕。

4 仿真校验

仿真校验中飞行器的基本参数如表1所示[8]。

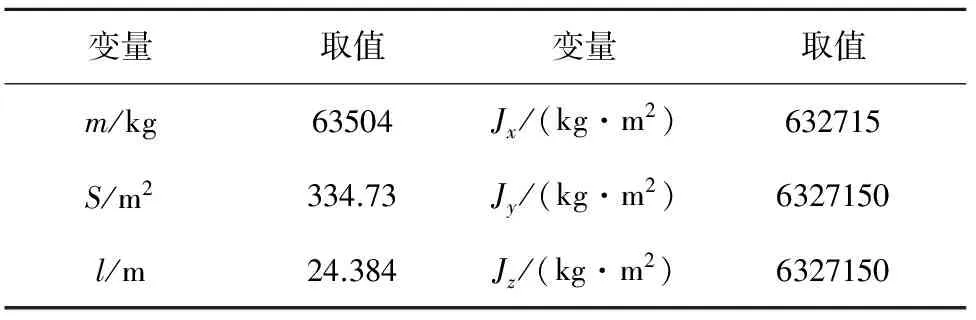
表1 飞行器基本参数

气动系数取值参考文献[14]。文中飞行器速度马赫数为6，飞行高度为20km。跟踪指令如表2所示。

表2 姿态角跟踪指令

初始值分别为α0=2°,β0=0.1°,γV0=1°。执行机构限幅为[-20°, 20°]，限速率为[-300°/s, 300°/s]。干扰观测器参数λ=20，滤波器参数T=diag(30, 30, 30)。控制器参数取值为

(34)

4.1 有效性校验及对比仿真

为了检验本文控制方法的有效性和鲁棒性，t=6s时在仿真中加入外界扰动为

(35)

分别采用本文的控制器(26)和不考虑耦合特性的控制器(29)进行仿真对比，结果如图1～4所示。

图1～3分别是姿态角、干扰估计和舵偏的对比变化曲线。

从图1可以看出，本文的控制方法保证了系统的渐近稳定跟踪，而且在相同的控制器参数下，相对于未考虑耦合特性的控制器NCBC，飞行器姿态系统实现了更快的上升时间和更小的超调量，获得了更好的动态性能。

由图1可知，在加入外部扰动的情况下，本文提出的CBC控制方法依然能够保证姿态角对跟踪指令的精确跟踪；而图2反映了干扰估计值对真值的跟踪情况，可以看出干扰估计值能够较快跟踪上真值，从而校验了本文所设计干扰观测器的有效性。仿真结果说明本文的高超声速飞行器姿态控制方法具有较强的鲁棒性。

表3列出了本文设计方法CBC和未考虑耦合特性的NCBC之间IAE性能指标的对比。从表3可以看出，三个通道中CBC方法相对于NCBC都具有更小的IAE指标，说明本文设计的控制方法使得姿态系统获得了更好的动态性能。

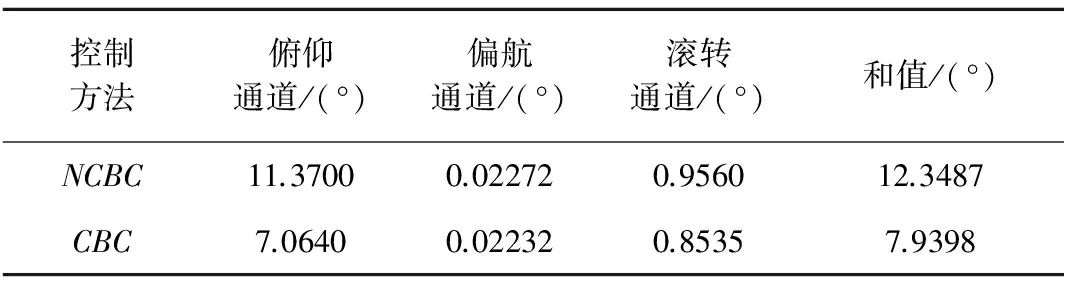
表3 IAE性能指标对比

从图3可以看出，系统的舵偏出现了一定程度的抖动。这同样是由于控制舵偏的速率限制和控制器中采用了切换项而导致的。实际仿真中可以考虑采用边界层方法将切换函数sgn(·)替换为饱和函数sat(·)，从而减小舵偏的抖振。

4.2 气动系数拉偏情况

采用本文的控制律，考虑气动系数拉偏，拉偏范围为±20%。为简便起见，仿真时间取为6s，仿真结果如图4～6所示。

图4～6分别是俯仰、偏航和滚动通道的姿态角以及舵偏的变化曲线。从图4可以看出，在正负拉偏情况下攻角均能够保证对跟踪指令的精确渐近跟踪，且具有良好的动态性能。同样地，图5和图6反映出偏航和滚动通道的良好动态特性。这说明本文设计的姿态控制器能够适应气动系数的不确定性变化，具有较强鲁棒性。

5 结 论

本文提出了一种新型的基于耦合特性的高超声速飞行器姿态控制方法，然后基于干扰观测器技术和滑模补偿增强了控制器的鲁棒性能。仿真校验了本文方法具有较好鲁棒性和动态性能。本文是作者对耦合性质及控制器设计的初步研究，在以后的工作中将进行进一步的理论拓展和深入研究。

[1] Duan H B, Li P. Progress in control approaches for hypersonic vehicle [J]. Science China - Technological Sciences, 2012, 55(10): 2965-2970.

[2] Charles E H, Yuri B S. Sliding mode disturbance observer-based control for a reusable launch vehicle[J]． Journal of Guidance，Control, and Dynamics, 2006, 29(6): 1315-1328．

[3] Georgie J, Valasek J. Evaluation of longitudinal desired dynamics for dynamic inversion controlled generic reentry vehicles [J]. Journal of Guidance, Control, and Dynamics, 2003, 26(5): 811-819.

[4] Su X F, Jia Y M. Self-scheduled robust decoupling control withH∞performance of hypersonic vehicles [J]. Systems Control & Letters, 2014, 70: 38-48.

[5] 周军, 刘玉玺, 周凤岐. 动态解耦和变结构鲁棒补偿的导弹再入控制[J]. 系统仿真学报, 2009, 21(10): 3071-3073, 3083. [Zhou Jun, Liu Yu-xi, Zhou Feng-qi. Study of missile reentry dynamic decoupling control based on variable structure robustness compensation [J]. Journal of System Simulation, 2009, 21(10): 3071-3073, 3083.]

[6] 周凤岐, 王延, 周军, 等. 高超声速飞行器耦合系统变结构控制设计[J]. 宇航学报, 2011, 32(1): 66-71. [Zhou Feng-qi, Wang Yan, Zhou Jun, et al. Design of variable structure controller for hypersonic coupled vehicle system [J]. Journal of Astronautics, 2011, 32(1): 66-71.]

[7] 孙向宇, 晁涛, 王松艳, 等. 考虑通道耦合因素的制导控制一体化设计方法 [J]. 宇航学报, 2016, 37(8): 936-945. [Sun Xiang-yu, Chao Tao, Wang Song-yan, et al. Integrated guidance and control design method considering channel coupling [J]. Journal of Astronautics, 2016, 37(8): 936-945.]

[8] 王建华, 刘鲁华, 汤国建. 高超声速飞行器俯冲段制导与姿控系统设计[J]. 宇航学报, 2016, 37(8): 964-973. [Wang Jian-hua, Liu Lu-hua, Tang Guo-jian. Guidance and attitude control system design for hypersonic vehicle in dive phase [J]. Journal of Astronautics, 2016, 37(8): 964-973.]

[9] Gigi S, Tangirala A K. Quantification of interaction in multiloop control system using directed spectral decomposition [J]. Automatica, 2013, 49(5): 1174-1183.

[10] Krstic M, Kanellakopoulos I, Kokotovic P V. Nonlinear and adaptive control design [M]. New York: John Wiley & Sons, 1995.

[11] 张天翼, 周军, 郭建国. 基于干扰观测器的高速飞行器预测控制律设计[J]. 航空学报, 2013, 35(1): 215-222. [Zhang Tian-yi, Zhou Jun, Guo Jian-guo. Design of predictive controller for hypersonic vehicle based on disturbance observer[J]. Acta Aeronautica et Astronautica Sinica, 2013, 35(1): 215-222.]

[12] Astrom K J, Hagglund T. PID controllers: theory, design and tuning [M]. Research Triangle Park, North Carolina: Instrument Society of America, 1995.

[13] Filippov A F. Differential equations with discontinuous righthand sides [M]. Dordrecht, the Netherlands: Kluwer Academic Publishers, 1988.

[14] Colgren R, Keshmiri S, Mirmirani M. Nonlinear ten- degree-of-freedom dynamics model of a generic hypersonic vehicle [J]. Journal of Aircraft，2009, 46(3) : 800-813.

通信地址：陕西省西安市碑林区友谊西路西北工业大学234邮箱(710072)

电话：(029)88493113

E-mail:Eason.work@qq.com

(编辑：牛苗苗)

Novel Coupling Based Attitude Control System Design for Hypersonic Vehicles

GUO Zong-yi, ZHOU Jun, GUO Jian-guo

(Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi’an 710072，China)

This paper presents a novel coupling characterization based robust control scheme for hypersonic vehicles. First of all, the attitude equations of a hypersonic vehicle are denoted, and the error dynamic model of the hypersonic vehicle is obtained based on the backstepping technique. Then, a robust coupling-based control scheme is proposed combining with the disturbance observer, and the asymptotic convergence is guaranteed through the sliding mode compensation. Finally, the integral absolute error (IAE) performance index is introduced, and the better performance of the proposed method is proven theoretically. The proposed method not only guarantees the asymptotic stability and the strong robustness, but also improves the dynamic performance via considering the coupling characterization into the controller design. The aerodynamic parameters perturbation and actual actuator constraints are considered in the numerical simulations, and the results demonstrate the validity of the control method in this paper.

Hypersonic vehicle; Coupling property; Disturbance observer; Sliding mode compensation; Integral absolute error (IAE)

2016-12-01;

2017-01-17

国家自然科学基金(61473226)

V448

A

1000-1328(2017)03-0270-09

10.3873/j.issn.1000-1328.2017.03.007

郭宗易(1988-)，男，博士生，主要从事飞行器制导控制与仿真研究。