煤矿水灾变坡巷道堵塞堆积体的力学特性

蒲文龙， 郝传波， 张国华

(1.黑龙江科技大学 安全工程学院， 哈尔滨 150022； 2.黑龙江科技大学， 哈尔滨 150022； 3.黑龙江科技大学 矿业工程学院， 哈尔滨 150022)

煤矿水灾变坡巷道堵塞堆积体的力学特性

蒲文龙1， 郝传波2， 张国华3

(1.黑龙江科技大学 安全工程学院， 哈尔滨 150022； 2.黑龙江科技大学， 哈尔滨 150022； 3.黑龙江科技大学 矿业工程学院， 哈尔滨 150022)

在分析煤矿突水灾区变坡巷道堵塞对应急救援有重要影响基础上，阐述了灾区变坡巷道堵塞特征，构建了灾区变坡巷道物理模型和力学模型。根据岩土工程边坡滑移相关理论，推导了堵塞堆积体与围岩外边界水平抗力、堆积体中任意一点位置处作用力计算公式，绘制了堆积体边界上的水平抗力分布曲线，以及堆积体中任意横向和纵向剖面上块体间相互作用力的分布曲线，进而描述堆积体内部不同区域内岩块的移动特征。该研究可为提高应急救援时效提供理论与技术支持。

矿井水灾； 变坡巷道； 堵塞； 力学特性

0 引 言

随着开采深度及强度的增加，我国煤矿水灾已成为继瓦斯灾害之后的第二类型的灾害[1-3]。矿井突水后，高压水流携带大量碎矸在灾区巷道轴线方向逐渐沉淀堆积，造成巷道堵塞。最易导致灾区巷道沉淀堆积的地点当属巷道变坡点，这是由于巷道变坡点的变向区段的阻挡作用所致。据统计，井下重大灾害第一现场瞬间死亡人员比例不到10%，其余绝大部分是因气体中毒、逃生路线阻断无法及时逃离、氧气逐步耗尽而窒息、救援通道受阻长时间得不到补给和及时救治等所致[4-6]。大量的矿井水灾实战案例表明，在煤矿井下灾后应急救援过程中，沿着原巷道进行救援是到达遇险人员驻留区最佳的救援路径，这也是矿井水灾应急救援决策中，即便遇到灾区巷道淤积堵塞仍将沿原巷道进行救援作为首选方案的主要原因。当前，煤矿水灾堵塞区原位开挖形成应急救援通道仍然采用人工挖掘的方法，不仅作业人员多、劳动强度大、作业效率低，而且容易导致堵塞区溃决诱发二次突水。为了提高灾区变坡巷道堵塞区开挖的应急救援时效，杜绝诱发次生灾害，对块体堵塞体的力学特性进行研究，成为变坡巷道堵塞体应急救援通道开挖的关键。

巷道堵塞一直以来被认为是生产过程中出现的巷道局部失稳现象，所以相关研究文献很少。已有研究[7-9]主要集中在三个方面：一是巷道掘进过程中遇到地质破碎带时的冒空处理；二是巷道在正常使用过程中出现局部支护失稳时的修复；三是煤与瓦斯突出、冲击地压等动力灾害发生后巷道的恢复。从其研究目的来看，均是满足生产需要，并非为了救援，研究内容多集中在处理方式上。因此，针对矿井突水灾区垮塌巷道以及在垮塌巷道内安全快速形成救援通道方面的研究，亟待广大学者、工程技术人员、救援人员给予足够重视。

基于此，笔者以解决矿井水灾应急救援过程中的关键问题为出发点，开展矿井水灾变坡巷道堵塞体力学特性研究，明确灾区变坡巷道堵塞体之间及堵塞块体与外围巷道之间的相互作用关系，为实现煤矿水灾灾区变坡巷道堵塞区段的安全、快速、有效应急救援提供理论和技术支持。

1 灾区变坡巷道堵塞体特征

煤矿突水形成堵塞体是产生于巷道中的一种由液体和固体组成的固-液两相流体[7-8]，固相物质由不同粒径区段的岩石块体组成，液相物质是水。在突水发生后，岩块介质在高压水的冲击携带搬运过程中，在灾区巷道变坡点形成具有一定粒度分布的松散堆积体，并形成堵塞。堵塞体呈现如下物理特征：堵塞体并非该位置处巷道围岩垮落体，而是在外力作用下从突水点运移过来的岩石块体，巷道自身处于稳定状态；高压水的水力携带输送作用，岩块沿着巷道轴向方向逐渐沉淀堆积，并且由于分选特性，较大岩块距离突水点位置较近，较小岩块会在距离突水点较远位置；灾区变坡巷道堵塞体由于分选原因，岩块三向尺寸相当、块径较小。灾区变坡巷道淤积堵塞状态及范围与巷道变坡长度L、巷道变坡角θ、巷道变坡高度h、变坡巷道断面尺寸与形状有关[10]，见图1。

图1 灾区变坡巷道堵塞

Fig. 1 Disaster area changing slope roadway block diagram

2 灾区变坡巷道堵塞体力学特性

矿井水灾发生后，预想在灾区变坡巷道堵塞体开挖应急救援通道，确定开挖方式、开挖位置、开挖断面形状与尺寸。安全、快速、有效开挖的前提是弄清如下几个问题：一是变坡巷道断面内堆积体与外围巷道作用力呈现的特点；二是堵塞堆积体内块体间作用力呈现的规律；三是堵塞堆积体不同区域内块体移动特点。

2.1 建立模型假设条件

建立变坡巷道堵塞堆积体力学模型，如图2所示。模型假设条件：

(1)为将问题简化，利用“散粒介质作为整体连续介质”的概念，用沿着散粒体任意截面上连续分布的假想力，来代替作用在散粒体接触点上的实际力。

(2)堆积体应急通道开挖是基于应急排水之后，因此，堆积体力学模型不考虑其后侧水压作用。

(3)堆积体含有表面水膜形成的表面张力可以忽略不计，即堵塞堆积体当做无水状态下的固相处理。

(4)堆积体是有周边限制且挡护作用下形成的，堆积体内部的作用力源自于岩块本身自重；变坡巷道外部围岩对内部堆积体的侧向作用力处于水平状态，源于堆积体堆积过程中的边坡滑移效应，且属于被动抗力。

图2 变坡巷道堵塞断面

由图2可知，灾区变坡巷道堵塞断面有两部分组成，一部分为矩形堵塞区域，另外一部分是半椭圆形堵塞区域。为研究方便，将堆积体断面用外接矩形来表示，如图3所示。

图3 堵塞区域外接矩形计算示意

2.2 被动抗力计算

根据岩土工程边坡滑移相关理论，堵塞堆积体在矩形断面稳定迹线的边界位置将受到外围围岩的限制，其间的作用力源于堆积力在边界位置处沿着自然堆积角在迹线的堆积下滑效应。如图4所示，考虑到对称性，取右半部分进行堵塞堆积体边界抗力分析。

图4 堵塞堆积体边界抗力计算示意

(1)

式中：a=B/2； b=H/2； B——变坡巷道断面宽度； H——变坡巷道断面高度。

设Q2点的坐标为(xQ2,yQ2)，Q2点距巷道底板的距离H1，则Q2点纵坐标yQ2为

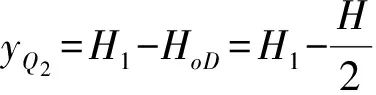
(2)

将式(2)代入矩形方程(1)，可求得Q2点的横坐标xQ2，设为w，即

xQ2=w。

(3)

设堆积体的自然堆积角为θ，则对于Q2，该点位置处的横向抗力Rx是由于MQ3Q2阴影部分堆积体沿Q3Q2迹线下滑而被动产生的。

将原坐标原点O向上平移到O1点，则原矩形在新坐标系中的方程为：

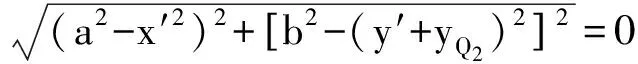
(4)

将式(3)代入式(4)，可推算y′，设为s,

y′=s ，

(5)

即在新坐标中，矩形满足方程

f(x′)=y′=s。

(6)

同时，在新坐标系中， 的直线方程为：

f(x′)=-tanθ·(x′-xQ2) ，

(7)

故，MQ3Q2阴影部分的重量

(8)

于是，图4阴影部分沿自然堆积角迹线Q3Q2下滑可简化为图5。

图5 堵塞体边界抗力计算

由于抗力Rx是沿Q3Q2迹线下滑而被动产生的，而自然堆积角θ是在堆积下滑之后所表现出来的，故简化图5中的块体与斜面Q3Q2之间的摩擦力为零，有下列等式成立：

Rx·cosθ=FMQ3Q2·sinθ，

即

Rx=FMQ3Q2·tanθ0，

(9)

由式(8)、(3)和(5)可知：

f(FMQ3Q2)=f(γ,θ,H1,H,B)。

据此可知，当灾区变坡巷道堵塞断面在距离巷道底部高度为H1的矩形垮落迹线上的Q2点处，该点的横向抗力Rx可通过式(8)、(3)和(5)联合求得，其值是距离巷道底板高度、堵塞堆积体容重、堵塞堆积体自然安息角、变坡巷道宽度与变坡巷道高度的函数。

于是，可获得灾区变坡巷道堵塞堆积体外边界位置处的抗力分布，如图6a所示，将其转化成直角坐标系，如图6b所示。

a

b

2.3 堵塞堆积体内块体间作用力分析

设定：

yP1=T ，

(10)

则堵塞堆积体中P点位置处的块体间纵向应力FP为

FP=γ·(yP1-yP)=γ·(T-yP) 。

(11)

为便于应用，设P点距离巷道底板的距离为hP，则：

(12)

将式(12)代入式(11)，整理得

通过分析可知，沿纵向(Ⅱ-Ⅱ剖线)方向上的块体间的压力Fy与其所处的埋深成正比关系，而在同一水平面得横向(Ⅰ-Ⅰ剖线)方向上，其各点的纵向压力Fx与其到堆积体上边缘的铅垂距离成正比关系。于是，可获得堵塞堆积体块体纵向之间作用力分布，见图8。

图7 块体间作用力计算

图8 块体间纵向作用力分布

由图8分析可知，其一，在距离巷道底板高度相同的位置上，堆积体中各点的纵向作用力相比较而言，纵向作用力受矩形堵塞体形态影响，均匀受力；其二，在距离矩形对称轴相同的距离位置处，同一纵向方向上堆积体中各点的纵向作用力相比较而言，距离巷道底部越近即埋深越大，其上的纵向作用力越大；第三，在距离巷道底板高度相同的位置上，纵向作用力轮廓与其上部堆积体的轮廓线形状基本相似，而在对称轴相同的距离位置处的同一纵向方向上，纵向力则自上而下呈现三角形轮廓。

2.4 堵塞堆积体内块体移动特征

根据对称性特点，在堆积体内部任意取自然堆积角迹线，见图9。在堆积体内部任意取自然堆积角迹线Q1Q3和Q3Q2，则在Q1位置处的水平抗力RxQ1是由位于其上部的MG1Q1Q3堆积体沿Q1Q3迹线下滑而产生的，而在Q2位置处的水平抗力RxQ2是由位于其上部的MG2Q2Q3堆积体沿Q2Q3迹线下滑而产生的。

据此类推，一直到巷道底部E1E2位置处，相应在E1位置处的水平抗力RxE1是由位于其上部的MG1E1O3堆积体沿E1O3迹线下滑而产生的，而在E2位置处的水平抗力RxE2是由位于其上部的MG2E2O堆积体沿E2O迹线下滑而产生的。相应自然堆积角迹线E1O、E1E2、E2O所圈定的三角形部分的堆积体则处于自然安息的无侧向滑动状态。由于堆积迹线E1DE2位于E1E2O自然堆积体下部，因此在E1DE2区域处于自然安息无侧向滑动状态。

根据以上分析，可将整个堆积体分成三部分，即无侧向滑动倾向的E1DE2O区、具有向两侧滑动倾向的MG1E1O区和MG2E2O区。在E1DE2O区，块体仅有纵向移动，没有横向移动。在MG1E1O区和MG2E2O区，块体既有纵向移动，也有横向移动。

以上对不同区域内块体位移趋势特征的分析，对后续救援通道开挖位置、开挖形状及尺寸优选提供依据。

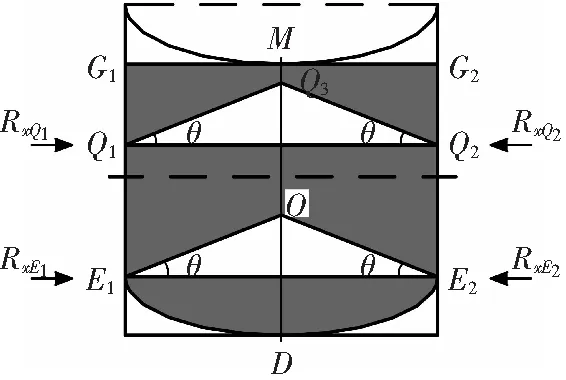
图9 堵塞堆积体内块体移动特征

Fig. 9Blockedaccumulationinbodyblockmovementcharacteristics

3 结 论

(1)堵塞堆积体并非该处围岩垮落体，而是外来岩石块体，巷道自身处于稳定状态；岩块沿着巷道轴向方向逐渐沉淀堆积，具有分选特性；灾区变坡巷道堵塞堆积体岩块三向尺寸相当、块径较小；灾区变坡巷道淤积堵塞状态及范围与巷道变坡长度、巷道变坡角、巷道变坡高度、变坡巷道断面尺寸与形状有关。

(2)在分析堵塞堆积体边界特征的基础上，从理论上推导了堵塞堆积体与围岩外边界水平抗力、堆积体中任意一点位置处作用力计算公式。

(3)给出堆积体边界上的水平抗力分布曲线，以及堆积体中任意横向和纵向剖面上块体间相互作用力的分布曲线。

(4)根据岩土工程边坡滑移相关理论，块体作用力源于变坡巷道边界位置处沿着自然堆积角在迹线的堆积下滑效应，进而描述了堆积体内部不同区域内岩石块体的移动特征，为应急救援通道开挖位置、开挖形状及尺寸优选提供依据。

[1] 周兴龙. 煤矿应急救援技术研究现状综述[J]. 科技资讯, 2007, 7 (2): 62-65.

[2] 李学来, 胡敬东. 煤矿应急救援技术的研究及应用现状[J]. 煤炭工程, 2005(4): 62-64.

[3] 宋元明, 刘志军, 王万生. 快速钻孔技术在煤矿应急救援中的实践[ J]. 中国安全科学学报, 2004, 14 (1): 63-65

[4] 郝传波, 张国华. 煤矿井下灾后救援中垮塌巷道研究的展望[J]. 黑龙江科技学院学报, 2012, 22(6): 549-552.

[5] 郝传波, 张国华. 顶板节理裂隙发育条件下回采巷道垮塌形态研究[J]. 黑龙江科技学院学报, 2013, 23(1): 28-33.

[6] 郝传波, 于会军, 张国华， 等. 井下断层地质破碎带巷道堆积体垮落形态[J]. 黑龙江科技大学学报, 2016, 26(3): 251-255.

[7] 左宏伟. 岩石块体滑动的界面摩擦阻抗时效研究[J]. 工程地质学报, 2000, 8(2): 154-159.

[8] 王思敬, 张菊明. 岩体结构稳定性的块体力学分析[J].地质科学, 1980(1): 19-32.

[9] 郝传波, 于会军, 张国华， 等. 井下断层地质破碎带巷道垮落体力学特性[J]. 黑龙江科技大学学报, 2016, 26(4): 351-357.

[10] 蒲文龙， 郝传波， 张国华. 煤矿突水灾区变坡巷道堵塞特征[J]. 黑龙江科技大学学报, 2016, 26(6): 573-577.

(编辑 晁晓筠 校对 李德根)

Study on mechanical properties of clogging deposit in mine flood changing slope point of roadway

PuWenlong1，HaoChuanbo2，ZhangGuohua3

(1.School of Safety Engineering, Heilongjiang University of Science & Technology, Harbin 150022，China； 2.Heilongjiang University of Science & Technology, Harbin 150022，China； 3.School of Mining Engineering, Heilongjiang University of Science & Technology, Harbin 150022，China)

This paper is based on an analysis of the important influence on emergency rescue due to a changing slope roadway congestion occurring in coal mine water inrush disaster area. The analysis consists of introducing the characteristics behind the changing slope roadway congestion in the disaster areas; developing physical and mathematical models on a changing slope roadway congestion in disaster area; deducing the calculation formula for the horizontal resistance found in accumulation body and surrounding rock, and force acting at any point in the accumulation body, according to the geotechnical slope sliding correlation theory; mapping the horizontal force distribution curve on the side of the deposit and distribution curve in any interaction between transverse and longitudinal profile block in deposits; and describing the characteristics behind the movement of the rock deposit within different area. This study may provide a theoretical and technical support for an improvement in emergency rescue.

mine flood; changing slope roadway; jam; mechanical properties

2016-12-09

国家自然科学基金项目(51374097； 51674107)

蒲文龙(1977-)，男，黑龙江省讷河人，副教授，博士研究生，研究方向：煤矿围岩控制与灾害防治、矿山爆破安全、煤矿应急救援等，E-mail：pwl0451@126.com。

10.3969/j.issn.2095-7262.2017.01.006

TD745

2095-7262(2017)01-0026-05

A