空间双柔性机械臂刚-柔耦合建模及定标误差分析
2017-03-30古青波李昂赵会光
古青波,李昂,赵会光
北京空间飞行器总体设计部,北京 100094
空间双柔性机械臂刚-柔耦合建模及定标误差分析
古青波*,李昂,赵会光
北京空间飞行器总体设计部,北京 100094
为研究空间多自由度机械臂在作大范围运动时臂杆柔性和关节柔性对末端定标精度的影响,考虑柔性臂杆的横/侧向弯曲变形所引起轴向伸缩的二次耦合项,采用计入集中质量的转子扭簧模型描述关节的柔性效应;提出了基于臂杆柔性的D-H参数法,递推出空间机械臂的柔性机构运动方程;应用Hamilton原理建立了空间双柔机械臂的一次近似刚-柔耦合动力学方程。对空间六关节双柔机械臂末端定标误差进行仿真,结果表明:臂杆的柔性和关节的柔性在空间机械臂的大范围运动中是相互耦合的;在工程应用中,需要将抓取目标设定在机械臂定标误差较小的方向上,以提高抓捕和操作的成功性。
空间机械臂;柔性臂杆;柔性关节;刚-柔耦合;定标误差
空间机械臂作为航天器在轨应用的重要操作执行工具,可用于大型复杂航天器的在轨装配与维修及空间站的舱段转位与交会对接,并可作为航天员在轨出舱工作的辅助工具,甚至可以替代航天员执行指定的任务1-2]。如图1所示为空间六关节机械臂构型,由关节、臂杆和末端执行器构成3]。
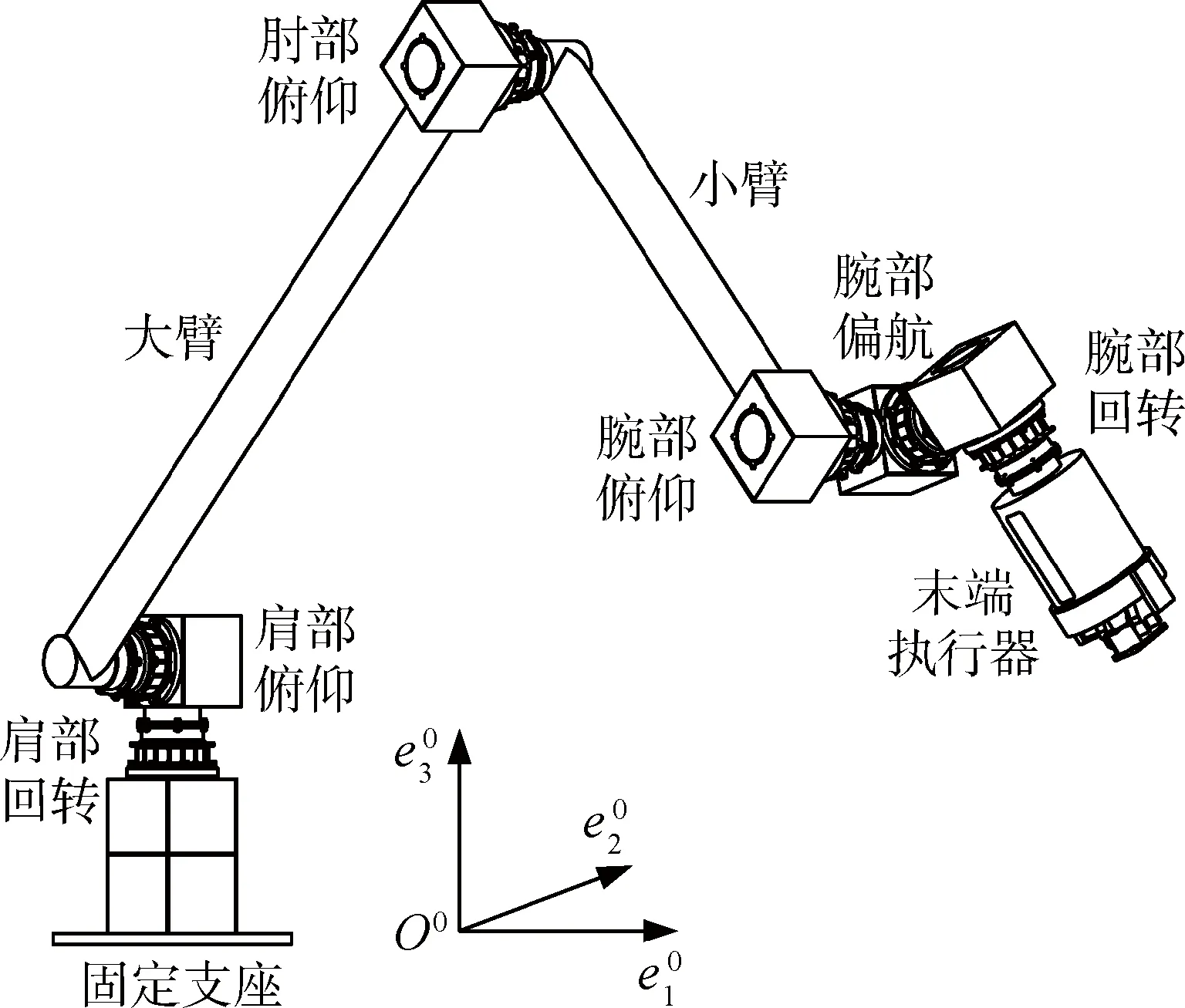
图1 空间两杆六关节机械臂构型Fig.1 Configuration of two arms and six joints space manipulator
空间机械臂在轨执行操作任务时,其末端对指定目标的定位精度是实现成功捕获的关键,而空间机械臂系统作为一种典型的链式无根多体系统,由于臂杆和关节的柔性效应,在作大范围刚性运动的同时会伴随臂杆的柔性变形,使系统呈现明显的刚-柔耦合特性,造成执行器在到达目标位置后,会存在小幅的残余振动,将严重影响空间机械臂的末端定标精度4-6]。为了实现空间机械臂系统更精准的操控,建立准确的空间双柔性机械臂动力学方程具有非常重要的理论价值和工程意义。
空间机械臂的柔性主要集中在柔性臂杆和柔性关节两部分7-9]。文献7]采用两套广义坐标分别描述机械臂的刚体运动和臂杆的柔性变形,柔性臂杆和柔性关节分别以杆单元和关节单元进行描述,但分析过程中未考虑二者的耦合作用;文献8]研究了由单臂杆和单关节所组成系统的全柔性耦合作用,并从中取得了一些有价值的规律,但对于复杂多杆和多关节的机械臂系统很难适用;文献9]利用柔性转子梁单元模型,综合考虑了柔性臂杆和柔性关节及其耦合作用的影响,但仅建立了平面柔性机械臂的动力学方程,且在分析过程中未计及动力刚化10]的一次耦合效应,对于空间大范围刚体运动的柔性机械臂分析时,会导致结果的发散。
本文以空间多自由度机械臂系统作为研究对象,在动力特性分析的过程中,计及臂杆和关节的双柔效应,采用计入臂杆柔性的D-H参数法进行空间机械臂的机构运动分析,应用Hamilton原理建立空间双柔性机械臂的一次近似刚-柔耦合动力学方程,并对臂杆柔性、关节柔性及双柔性对机械臂末端定标精度的影响进行了仿真分析。
1 空间双柔性机械臂刚-柔耦合动力学建模
1.1 柔性机械臂的变形关系描述

(1)
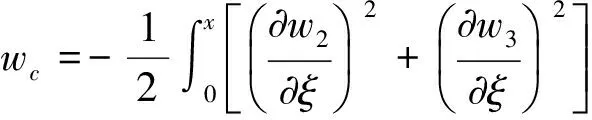
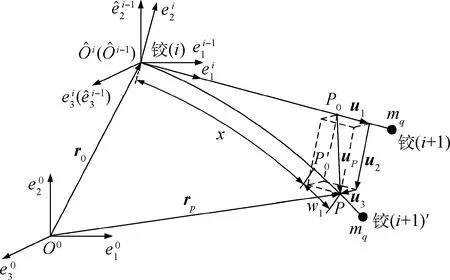
图2 空间机械臂柔性臂杆等效力学模型Fig.2 Equivalent mechanical model of space manipulator flexible arm
应用一致质量有限元离散化原理,可将单元的变形量w用插值形函数12]表示,则柔性臂杆中心轴线上任意点P在浮动基下的变形位移矢量可表示为:
(2)

1.2 柔性机械臂的机构运动学描述
采用计入臂杆柔性效应的D-H参数法对空间机械臂系统进行运动学分析,如图3所示,各坐标系13]确立方式如下:

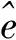
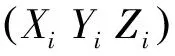
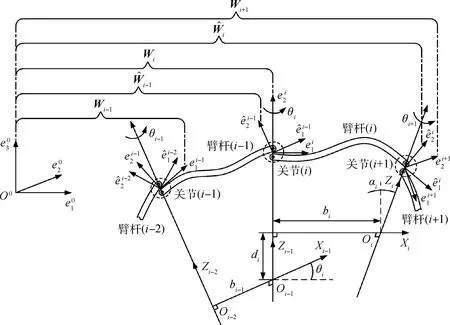
图3 计入柔性效应的D-H坐标系及转换矩阵示意Fig.3 D-H coordinate and transformation matrix schematic included flexible effects
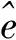
(3)
式中:
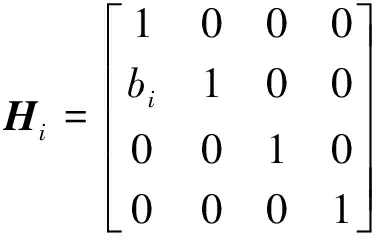
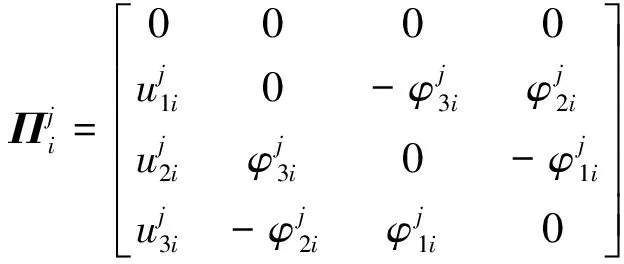
(4)

(5)
将式(5)对时间求导,即可得到点P相对于基准坐标系的速度和加速度为:
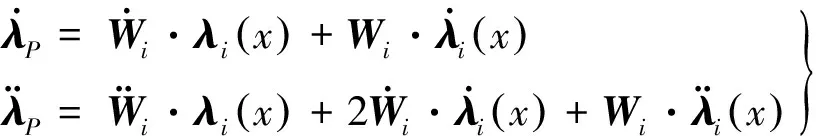
(6)
由Wi=Wi-1Ei-1Ai可得:
1.3 柔性关节的动力特性描述
在小变形情况下,柔性关节可以等效为“齿轮减速器-弹性扭簧”模型14],如图4所示。令qi为臂杆i的理论转角,θi为臂杆i的实际转角,εi为弹性扭簧所引起的变形转角,则有θi=qi+εi,若齿轮减速器的传动比为ni,则qi=ωi/ni,其中ωi为关节驱动电机转子的转角。
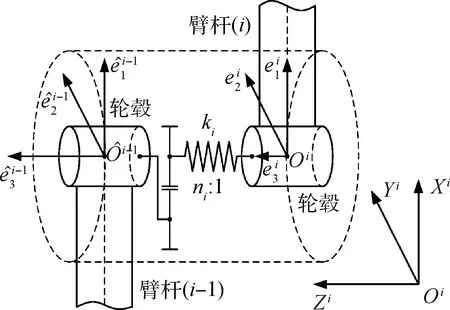
图4 空间机械臂柔性关节等效模型Fig.4 Flexible joint equivalent model of space manipulator
(7)
(8)
1.4 空间双柔性机械臂的刚-柔耦合动力学方程
应用Hamilton原理建立空间双柔机械臂的刚-柔耦合动力学方程15]:
(9)
式中:T为系统的总动能:U为系统的总势能:W为系统外力所做的功。系统的总动能T主要包括柔性臂杆的动能Tb和柔性关节的动能Tr;系统的总势能U主要包括柔性臂杆的势能Ub和柔性关节的势能Ur;系统外力所做的功W为各关节驱动力矩MH所做的总功。
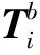
(10)
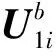
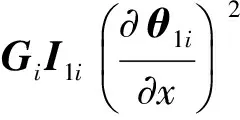
(11)
(12)
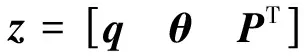
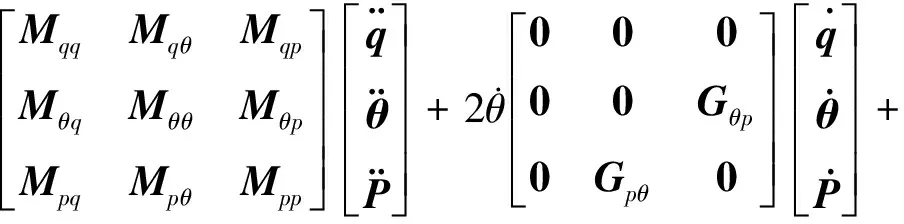
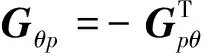
2 空间双柔性机械臂末端定标误差仿真计算与分析
对图1所示的空间两杆六关节械臂在抓捕目标过程中的末端定标误差进行仿真计算与分析。空间机械臂的D-H参数及坐标系的建立如图5所示。各给定参数如下:柔性臂杆的长度为b1=2 m、b2=1.8 m,截面积为A=8×10-3m2,密度为ρ=1.7×103kg/m3,弹性模量为E=90 GPa,泊松比为u=0.3;各关节的质量为m=5 kg,转子的转动惯量为J=1.25×10-2kg·m2,关节驱动的减速比为n=10,柔性关节的扭转弹性刚度系数为k=2.5×103N·m/rad。不计空间微重力影响。
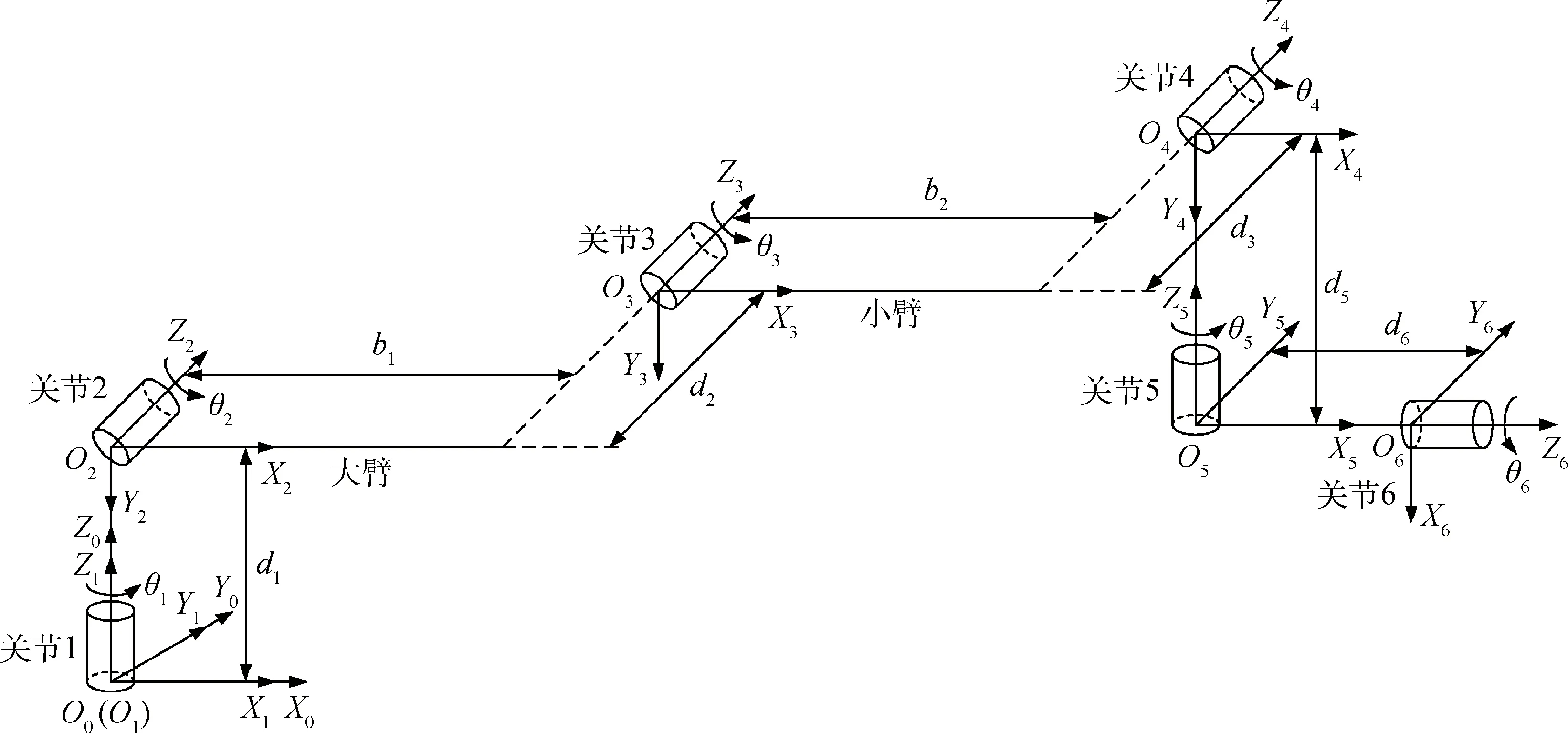
图5 空间两杆六关节机械臂D-H坐标系机构简图Fig.5 D-H coordinate mechanism chart of two arms and six joints space manipulator
空间双柔性机械臂系统各关节初始角度和角速度均为0,各关节的驱动控制力矩为:

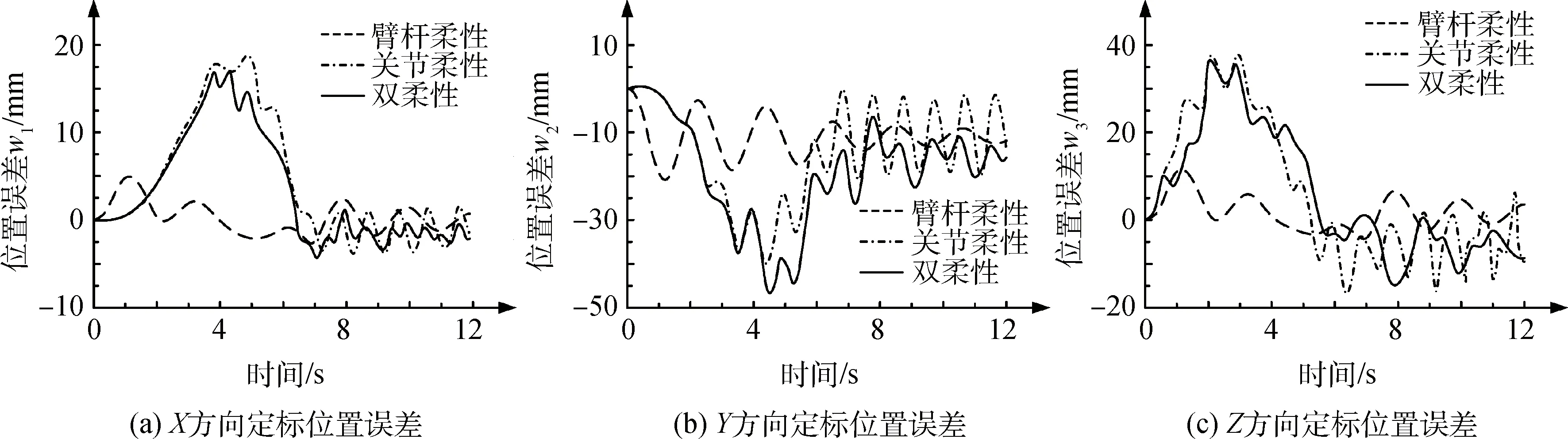
图6 空间双柔性机械臂的末端定标位置误差Fig.6 Terminal calibration position error of space arm
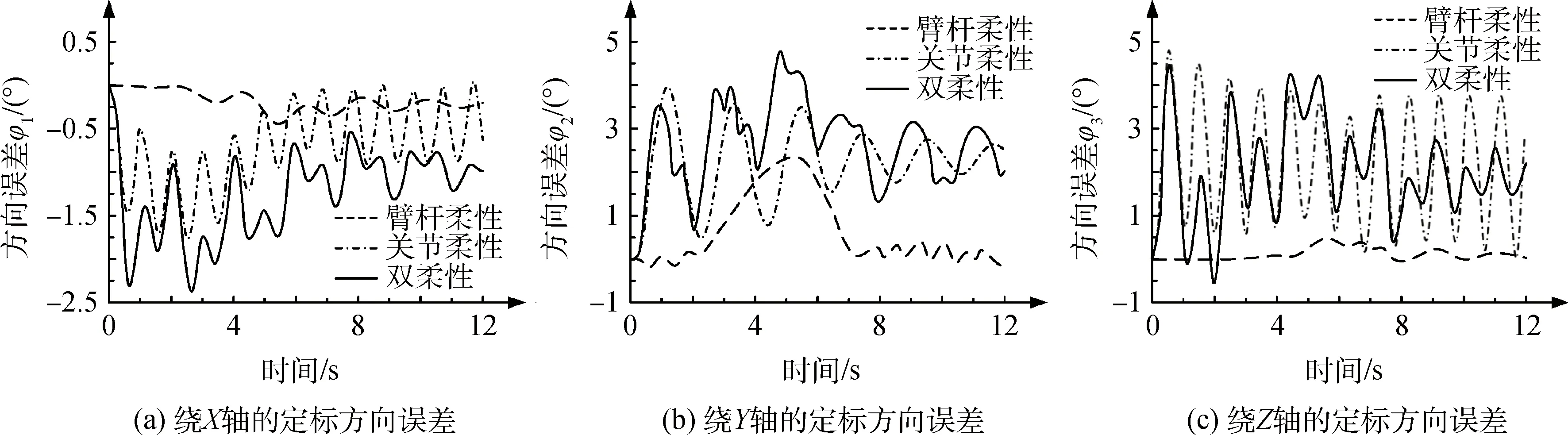
图7 空间双柔性机械臂的末端定标方向误差Fig.7 Terminal calibration direction error of space arm
仿真结果图6和图7给出空间双柔性机械臂末端定标的位置误差和方向误差,由于臂杆和关节柔性效应所引起机械臂末端定标的位置误差和方向误差均比较大。机械臂在运动过程中,Y方向的位置误差最大,最大值出现在4.5 s,约为45 mm;X方向的位置误差最小,最大值出现在4 s,约为17 mm。绕Z轴的方向误差最大,最大值出现在4.5 s,约为4.5°;绕X轴的方向误差最小,最大值出现在2.8 s,约为2.3°。机械臂在运动结束后,末端依然存在一定幅度的残余振动,Y方向残留的位置误差最大,约为15 mm;X方向残留的位置误差最小,约为2.3 mm;绕Z轴残留的方向误差最大,约为2.5°;绕X轴残留的方向误差最小,约为0.9°。
3 结束语
在空间多自由机械臂动力特性的分析中,计及了臂杆和关节的双柔效应,采用基于臂杆柔性变形的D-H参数法,递推出空间机械臂的柔性机构运动学方程,应用Hamilton原理建立了空间双柔性机械臂的一次近似刚-柔耦合动力学方程,并对机械臂的末端误差进行了仿真分析。可得出结论:
1)在空间多自由度双柔性机械臂动力特性的分析中,计入了臂杆横/侧向弯曲变形所引起轴向变形的二次耦合项,采用基于臂杆柔性变形的D-H参数法,分析了柔性机械臂的运动特性,所建立的双柔性一次近似刚-柔动力学方程为空间机械臂末端定标误差的分析提供了更准确数学模型。
2)空间多自由度双柔性机械臂在运动过程中,由于臂杆和关节的柔性所引起末端定标的位置误差和方向误差并不独立,而是相互耦合的;通过单独去分析二者的柔性效应,再进行简单的叠加,并不能真实地反映出空间机械臂的双柔特性。
3)空间多自由度双柔性机械臂末端定标的位置误差和方向误差在不同的方向上存在较大的差异,在工程实际应用中,可以将抓取目标设定在空间机械臂定标误差较小的方向上,从而提高机械臂末端抓捕和操作的成功性。
References)
[1] 赵志刚,赵阳,葛卫平,等.空间站机械臂转位系统动力学建模及特性分析J].中国空间科学技术,2013,33(3):22-29.
ZHAO Z G,ZHAO Y,GE W P,et al.Dynamic modeling and characteristics analysis for manipulator transformation system of the space stationJ].Chinese Space Science and Technology,2013,33(3):22-29(in Chinese).
[2] 于登云,潘博,孙京.空间机械臂关节动力学建模与分析的研究进展J].航天器工程,2010,19(2):1-10.
YU D Y,PAN B,SUN J.A literature review on dynamic modeling and analysis of the joints in space manipulatorJ].Spacecraft Engineering,2010,19(2):1-10(in Chinese).
[3] 贾宏亮,姚琼,黄强.基于质量分配的空间机械臂刚度优化J].中国空间科学技术,2008,28(3):45-52.
JIA H L,YAO Q,HUANG Q.Stiffness optimization of space manipulator based on mass allocationJ].Chinese Space Science and Technology,2008,28(3):45-52(in Chinese).
[4] 徐文福,杜晓东,王成疆,等.空间机械臂系统总体技术指标确定方法J].中国空间科学技术,2013,33(1):53-60.
XU W F,DU X D,WANG C J,et al.Determination method of overall technology index for space manipulatorJ].Chinese Space Science and Technology,2013,33(1):53-60(in Chinese).
[5] 潘冬.空间柔性机械臂动力学建模分析及在轨抓捕控制D].哈尔滨:哈尔滨工业大学,2014:2-8.
PAN D.Research on dynamics modeling and capture control of space flexible manipulatorD].Harbin:Harbin Institute of Technology,2014:2-8(in Chinese).
[6] 徐拴锋,杨保华,张笃周,等.面向非合作目标抓捕的机械臂轨迹规划方法J].中国空间科学技术,2014,34(4):8-15.
XU S F,YANG B H,ZHANG D Z,et al.Trajectory planning algorithm for manipulators capturing non-cooperative objectsJ].Chinese Space Science and Technology,2014,34(4):8-15(in Chinese).
[7] MODI V,CHAN J.Performance of an orbiting flexible mobile manipulatorJ].Mechanical Design,1991,1(13):516-524.
[8] XI F,FENTON R.Coupling effect of a flexible link and a flexible jointJ].Journal of Robotics Research,1994,13(5):443-453.
[9] YUE S G,YU Y Q,BAI S X.Flexible rotor beam element for the manipulators with joint and link flexibilityJ].Mech Mach.Theory,1997,32(2):209-219.
[10] KANE T R,RYAN R R,BANER-JEE A K.Dynamics of acantilever beam attached to a moving baseJ].Journal of Guidance,Control of Dynamics,1987,10(2):139-151.
[11] RYU J,KIM S S.A general approach to stress stiffening effects on flexible multibody dynamic systemsJ].Mechanics of Structures and Machines,1994,22(2):157-180.
[12] 刘锦阳.刚-柔耦合动力学系统的建模理论研究D].上海:上海交通大学,2000 :15-26.
LIU J Y.Study on dynamic modeling theory of rigid-flexible coupling systemsD].Shanghai:Shanghai Jiaotong University,2000:15-26(in Chinese).
[13] ZHANG D G.Recursive Lagrangian dynamic modeling and simulmion of multi-link spatial flexible manipulator armsJ].Applied Mathematics and Mechanics,2009,30(10):1283-1294.
[14] SPONG M W.Modeling and control of elastic joint robotsJ].Journal of Dynamic,Measurement and Control,1987,109(4):310-319.
[15] SHARF I.Geometric stiffening in multibody dynamics formulationsJ].Journal of Guidance,Control of Dynamics,1995,18(4):882-890.
[16] 陈思佳.刚-柔耦合问题与空间多杆柔性机械臂的动力学建模理论研究D].南京:南京理工大学,2012:69-74.
CHEN S J.Researches on the rigid-flexible coupling problem and the dynamic modeling theory of multi-link spatial flexible manipulator armsD].Nanjing:Nanjing University of Science & Technology,2012:69-74(in Chinese).
(编辑:车晓玲)
Rigid-flexible coupling modeling and calibration error analysis of the space double flexible manipulators
GU Qingbo*,LI Ang,ZHAO Huiguang
BeijingInstituteofSpacecraftSystemEngineering,Beijing100094,China
To study the impact of the arm and joint flexibility on the terminal calibration precision when the space multi-degrees of freedom manipulator did spatial motion in a large range,considering the secondary coupling term of axial stretching caused by the flexible arm horizontal/lateral bending deformation,a D-H method was proposed based on flexible arm by using a rotor torsion-spring model including lumped mass to describe the flexible effect of joints.The flexible mechanism movement equation of space manipulator was proposed.The first approximation rigid-flexible coupling dynamics equations of space double flexible manipulator was established by using the Hamilton principle.The simulation of the terminal calibration error of the space six joints double flexible manipulator was carried out.The results show that:arm and joint flexibility are coupled when the space manipulator is in a large range movement.To improve the success of the capture and operation,the fetching targets should be set in the direction with a smaller calibration error of manipulators in engineering applications.
space manipulator;flexible arm;flexible joint;rigid-flexible coupling;calibration error
10.16708/j.cnki.1000-758X.2017.0011
2016-06-27;
2016-10-13;录用日期:2016-11-24;
时间:2016-12-16 11:29:22
http:∥www.cnki.net/kcms/detail/11.1859.V.20161216.1129.012.html
古青波(1987-),男,工程师,gob06071202@163.com,研究方向为航天器总体设计、结构与机构设计
古青波,李昂,赵会光. 空间双柔性机械臂刚-柔耦合建模及定标误差分析J].中国空间科学技术, 2017,37(1):33-40. GU Q B,LI A,ZHAO H G. Rigid-flexible coupling modeling and calibration error analysis of the space double flexible manipulators J].Chinese Space Science and Technology, 2017,37(1):33-40 (in Chinese).
V423.7;TP241.3
A
http:∥zgkj.cast.cn
