基于行为的非合作目标多航天器编队轨迹规划
2017-03-30王涛许永生张迎春谢成清
王涛,许永生,张迎春,*,谢成清
1.哈尔滨工业大学,哈尔滨 150001 2.深圳航天东方红海特卫星有限公司,深圳 518057
基于行为的非合作目标多航天器编队轨迹规划
王涛1,2,许永生2,张迎春1,2,*,谢成清2
1.哈尔滨工业大学,哈尔滨 150001 2.深圳航天东方红海特卫星有限公司,深圳 518057
目前航天器编队轨迹规划的研究并未综合考虑目标非合作性、构型复杂性及控制协同性等问题,针对非合作目标多航天器编队系统,提出了一种基于行为的相对运动轨迹规划方法。首先,基于聚集行为模型设计了期望运动场,将期望速度视为一系列具有不同行为特性的速度矢量和,通过构造平衡态构型公式计算行为调节参数。其次,采用高斯型环境函数描述了非合作目标特性,并通过C-W方程对期望运动场进行了改进,使得该方法在多航天器编队系统与非合作目标形成期望构型的过程中,既能避免编队成员之间发生碰撞,又能保证与非合作目标之间的安全距离。仿真结果表明,该算法可以使多航天器编队系统在3 000 s内运动至期望构型。该方法在复杂的、多个控制目标的编队飞行轨迹规划中优势明显,具有自主性、协同性、鲁棒性强等特点,同时可应用于不同类型的编队构型相对运动规划。
行为策略;非合作目标;多航天器编队;碰撞规避; 轨迹规划
随着航天技术的飞速发展,以航天器在轨监视与维护、太空垃圾清理为目的的自主在轨服务技术受到高度重视,由多个成员组成的编队系统对非合作目标进行监视、维护等操作是一种可行并具有良好前景的在轨服务形式。由于系统的“群”特性与非合作特性,使得系统的相对运动轨迹规划成为一项急需解决的关键问题1,2]。
由于非合作目标的运动和结构的不确定性,会给编队飞行带来很大的碰撞可能性,因此很多学者将碰撞问题作为主要约束开展相对运动轨迹规划算法的研究。文献3]针对编队卫星在构型重构和构型失效重组时发生碰撞可能性最大的两种机动工况,采用数学规划的方法对其进行防碰撞规避准则、规避策略和控制方面的研究。文献4-5]将人工势函数制导方法应用于航天器的非合作自主交会对接任务和动态障碍物躲避问题。文献6]将相对运动模型建立在追踪星轨道坐标系上,设计了自主接近控制律,并用李雅普诺夫稳定性理论证明其有效性。
目前的非合作目标编队飞行轨迹规划算法主要还集中在双星或三星编队任务,虽然考虑了非合作目标的防碰撞约束,但是针对多星复杂编队构型的协同轨迹规划算法研究较少。文献7]将行为方式应用到多机器人编队系统,设计了机器人编队基于行为方式运动的试验方法,从而使行为方式控制策略进入到编队研究者的视野。文献8]中分析了通信受限的情况下,编队航天器利用行为策略进行路径规划的问题,给出了分布式的追踪策略,但是未结合具体轨道运动特性开展研究。文献9]提出了一种基于行为的太阳帆群编队路径规划算法,但是研究过程中仅考虑了编队成员之间的防碰撞问题,并未涉及与非合作目标之间的碰撞避免问题。
本文基于行为策略思想,分析了聚集行为模型,在考虑了目标非合作特性和轨道运动的情况下,设计了空间非合作目标编队飞行期望运动场,并以此为基础进行了相对运动轨迹规划。该方法适合复杂的、多个控制目标的多航天器编队系统,可广泛适用于不同类型的编队运动规划。
1 聚集行为模型
对于n维欧氏空间中由N个航天器组成的编队系统,令xi∈n描述航天器i的位置矢量。假设各航天器同时运动(无时延),且知道彼此的精确位置,则考虑连续时间运动动力学的个体运动方程为:
(1)
式中:g:n→n为描述个体之间相互作用的吸引/排斥函数,其一般形式定义如下:
(2)
式中:‖y‖为欧几里得范数;ga:+→+描述吸引项的大小,且在大范围内有效;gr:+→+描述排斥项大小,在小范围内起作用。这里定义的函数g(·)为奇函数(相对原点对称),即满足,正是这一重要特性使得编队系统产生聚集行为。
假设吸引/排斥函数分别存在对应的势函数为Ja:+→+与Jr:+→+,且满足:
(3)
因此个体i的运动动力学可写作:
(4)
2 基于行为策略的编队飞行轨迹 规划
本文基于行为思想构建了一个定义期望速度的动力学系统,将期望速度视为一系列具有不同行为特性的速度的矢量和,通过每个子航天器自主确定其在构型中的预期最终位置来实现编队构型。
2.1 期望运动场设计
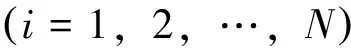
1)聚集行为:针对N个期望位置点引入N个不同的全局吸引作用。基于该行为的个体i的期望速度一般形式为:
(5)
式中:ψG:+→+是依赖于个体与期望位置距离的函数;为所有N个效应的加权和;c1,c2,…,cN分别为权重参数;cj为仅依赖于期望位置而不依赖于个体的参数。定义聚集行为的主要目的在于使得编队中各航天器收拢聚集,因此希望聚集行为在大范围内均产生作用。
2)驻留行为:针对N个期望目标点引入N个不同的局部吸引作用。基于驻留行为的期望速度场仅在吸引域附近存在不可忽视的作用,引入kD定义驻留行为影响球半径,则该行为的数学表达式为:
(6)
式中:ψD同样定义了一个从正实数到正实数的映射,但在超出给定影响球作用时为0。驻留行为与聚集行为相比是一个局部作用函数,仅在最后逼近终端位置时起作用。同样的dj仅依赖于目标的终端位置,与个体位置无关。
3)避让行为:用于描述两个个体在相互逼近时的行为,其期望速度差表现为排斥作用。数学表达式为
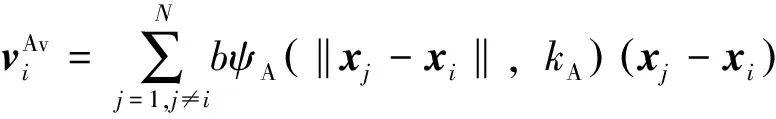
(7)
式中:ψA定义了从正实数到正实数的映射;kA定义了碰撞避免行为的安全影响球。当个体之间距离相对安全距离而言较大时,有ψA=0。
基于上述3种行为定义,对于由N个目标点组成的期望编队,编队中个体i在任意时间的期望速度是所有行为速度的线性加权求和,依赖于权重参数cj,dj,写作:
(8)
对于整个编队系统而言,其期望速度可简单定义为:
(9)
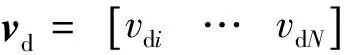
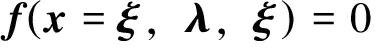
(10)
通过求解这一线性方程组,可方便通过系统平衡态寻找适合的参数λ。该公式由N个矢量方程组成,每个方程对应于一个特定目标位置ξi:
(11)
式中:未知量为参数,因此可写成关于未知量的平衡态构型公式的形式:
(12)
式中:矩阵E与向量g依赖于所选择的函数ψ与参数b,ψ用于描述关于目标位置ξ的各种行为。上述方程组实际上为3N个线性标量方程,其中包含2N个未知参数cj、dj,因此通常无法得出可行解,除非部分方程之间存在一定线性关系。这也说明了使用该方法不能完全实现所有可能的构型,构型需要具有对称性。一般可以通过给定ci=cj(或di=dj),进而求解其他未知参数。
3种行为函数的具体形式将影响算法的计算效率,本文将聚集行为定义为线性函数,驻留行为与避让行为定义为指数函数,其形式分别为:
(13)
为验证方法的有效性,假设编队系统由8个航天器组成,各成员初始时刻在距目标500m距离的50m空间范围内自由分布,期望构型以原点为中心,分别形成边长为12m的正立方体编队构型和正八边形构型。仿真参数设置如表1所示。
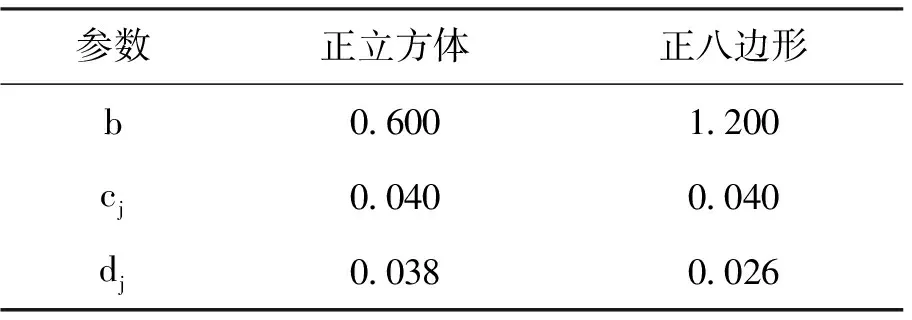
表1 仿真参数
规划得到的正立方体构型和正八边形构型编队运动轨迹如图1所示,仿真结果表明,该算法可实现编队向期望构型的机动与聚集,期间保证了航天器之间的碰撞避免,验证了该算法的有效性。
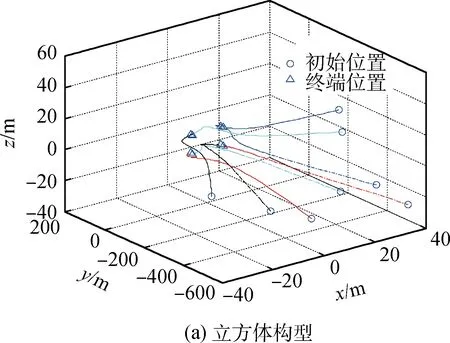
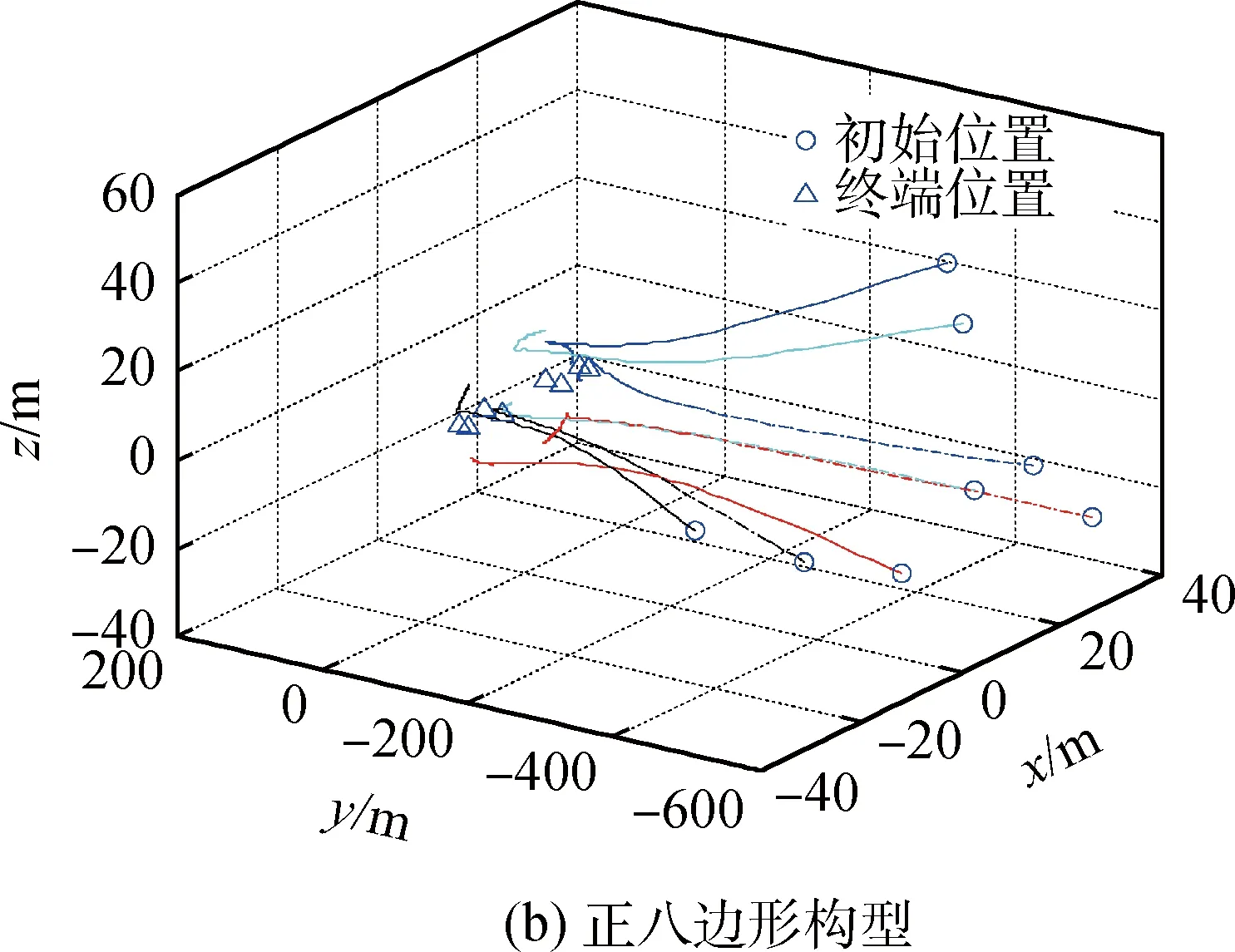
图1 立方体构型和正八边形编队飞行转移轨迹Fig.1 Transfer trajectory of cube and octagon configurationformation flying
2.2 考虑非合作目标碰撞避免的外部环境影响 分析
由于编队系统实际运动时要与非合作目标进行编队飞行,除了个体之间的交互之外,编队成员的运动需要避免与非合作目标发生碰撞,数学上可以采用环境势函数σ:n→对非合作目标带来的外部环境影响进行描述。本文将非合作目标看作障碍球体,选取高斯型环境势函数来描述由于非合作目标带来的外部环境影响。高斯型环境势函数形式可定义为:
(14)
其中,Aσ∈,lσ∈+。与梯度与编队中心运动分别计算如下:
(15)
则考虑非合作目标碰撞避免的期望速度为:
(16)
2.3 考虑轨道运动的期望速度场改进
以上设计的一般情形下期望速度场并未考虑轨道运动特性。下面考虑轨道特性进行期望速度场改进。
考虑近圆轨道,由C-W方程得到控制力为零且忽略摄动的情况下,有:
(17)
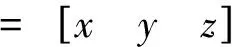
(18)
其中,A,B,C,D矩阵具体形式为:
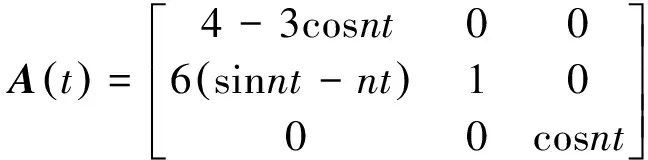
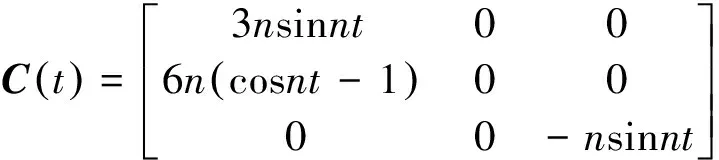

这一解析解实际上定义了引力场作用下实现期望构型的一种新的聚集行为。对于给定航天器,希望其在td时刻后到达所期望的位置点ρd,由式(18)可得:
(19)
基于这一考虑,对于空间中每个位置xi以及期望构型对应的每个目标点ξi,可定义聚集行为速度矢量为:
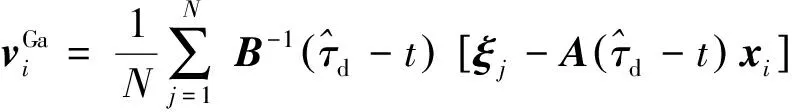
(20)
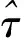
外段远离期望构型位置时,聚集行为考虑引力场作用:
(21)
内段在距离目标位置较近时,Gather行为采用式(13)中所示线性函数:
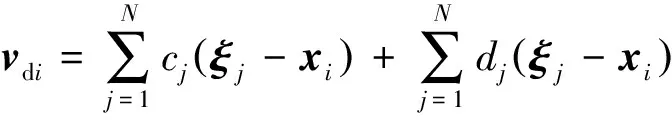
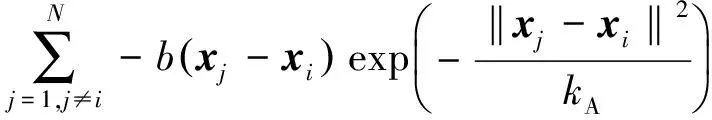
(22)
3 仿真算例
假设非合作目标运行于地球同步轨道,由5颗航天器组成的编队系统在非合作目标正后方1 000m的空间内任意分布,非合作目标的安全空间近似为半径3m的球,将描述与非合作目标碰撞避免的高斯函数对应的参数设为Aσ=2,lσ=16,驻留行为函数和避让行为函数的安全作用距离分别为kA=10 m,kD=10 m,编队系统的期望构型为以非合作目标为中心的金字塔构型,编队系统初始构型和期望构型如表2所示。
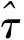
b=5.520 6,cj=c0=3.2×10-4
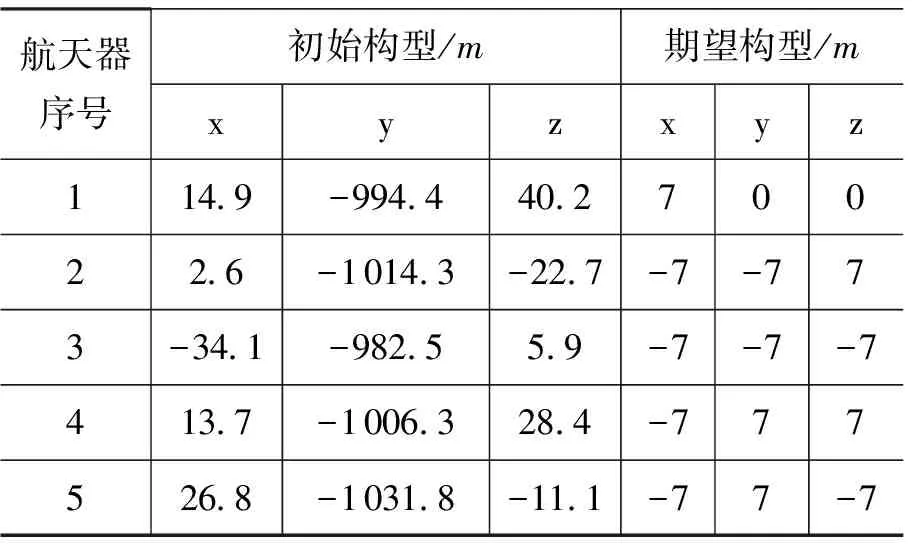
表2 编队系统初始构型和期望构型
仿真结果如图2~图4所示,通过仿真结果可知,编队系统到达期望构型的收敛时间为2 995s,实现了在有限时间内完成向期望构型的相对运动转移,避免了各成员间碰撞的同时,各航天器在非合作目标附近绕行,实现了与非合作目标的碰撞避免。
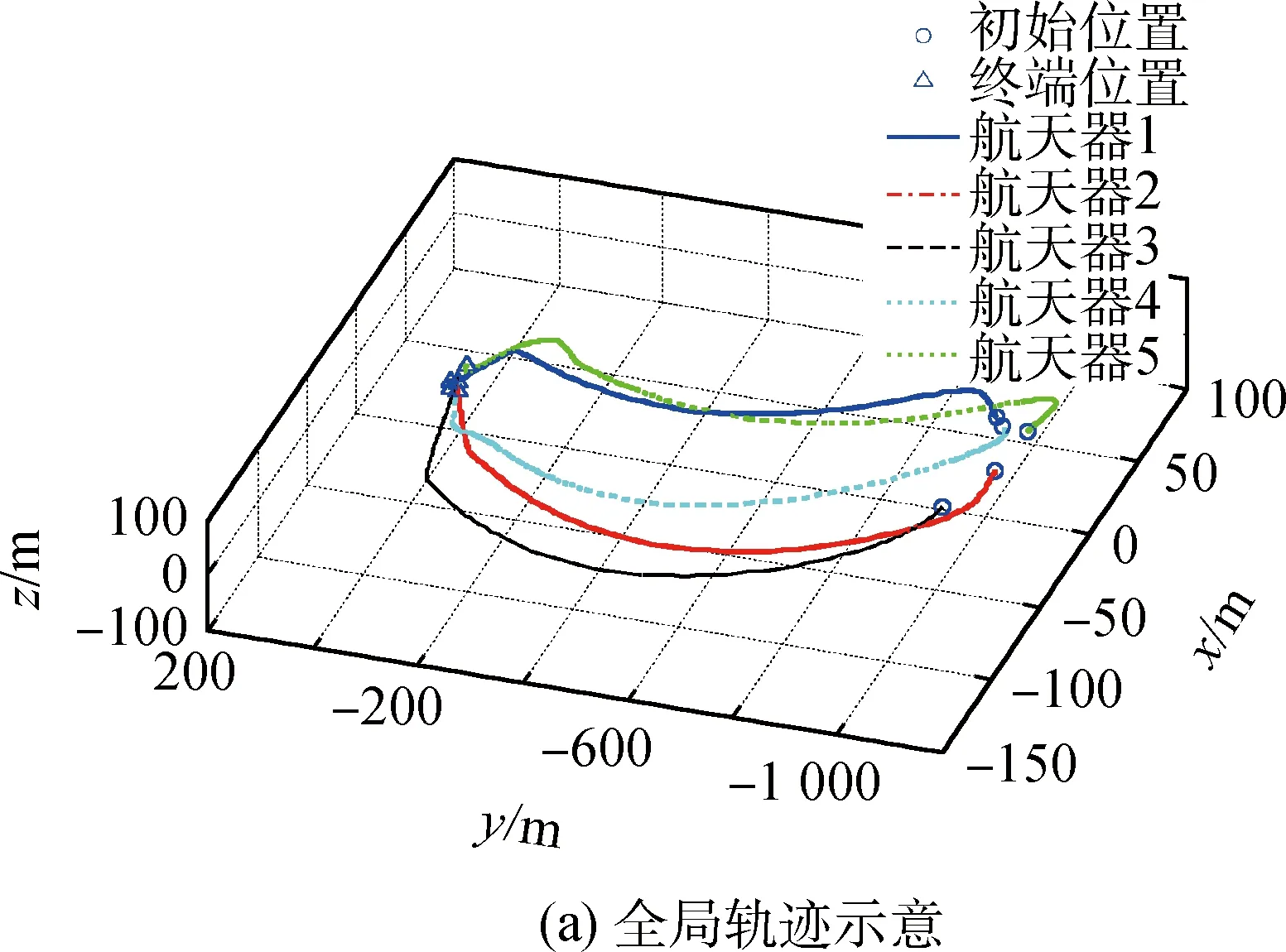
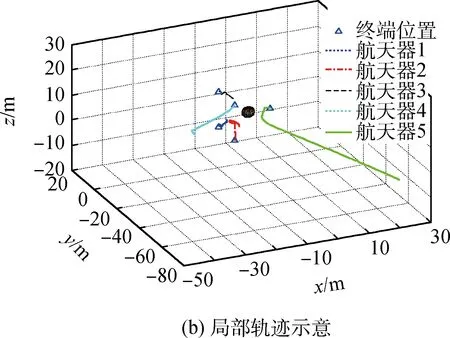
图2 相对运动转移轨迹全局和局部示意Fig.2 Global track and partial track of the relative motion
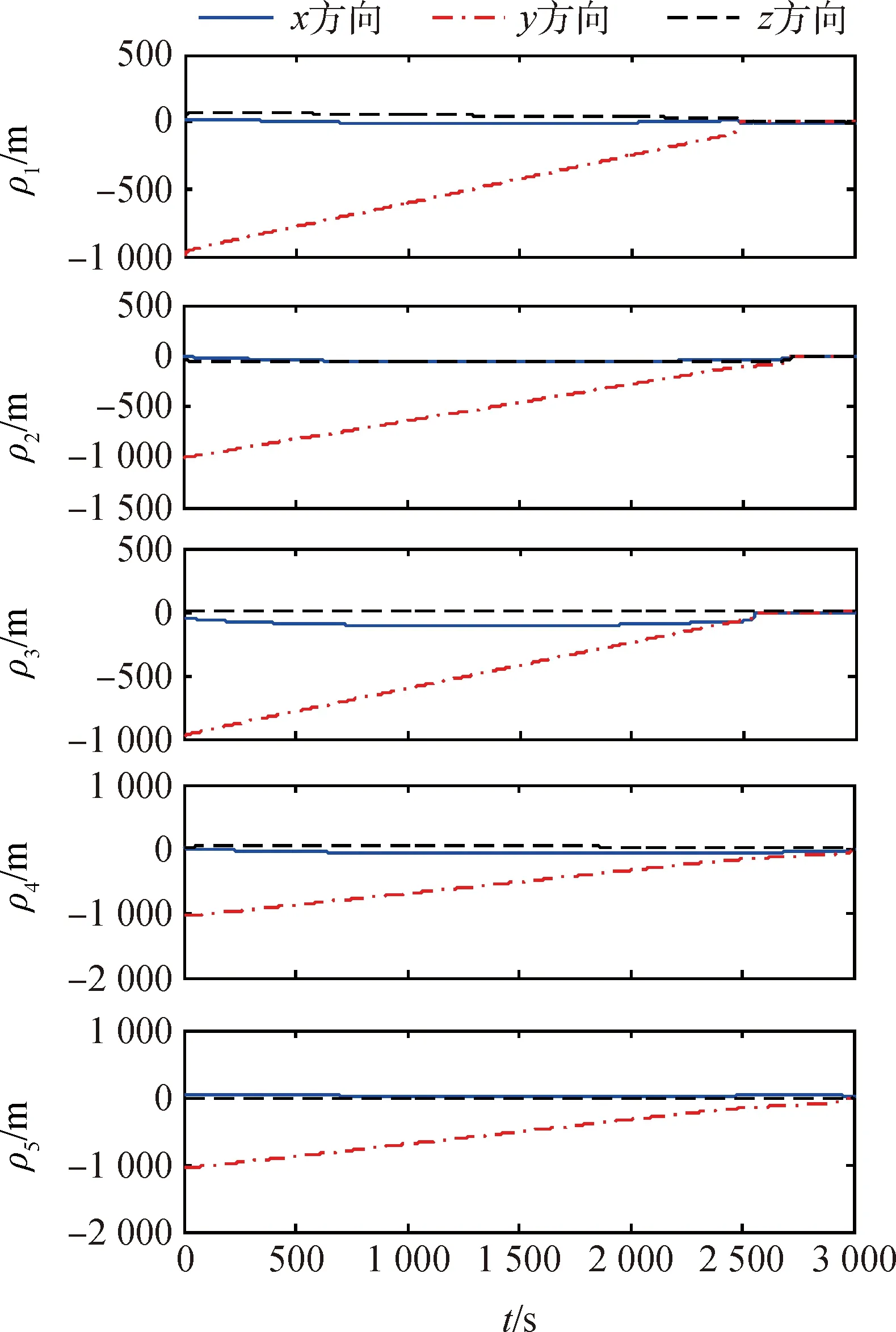
图3 各成员相对非合作目标的位置变化Fig.3 Position variation of members relative to the non-cooperative target
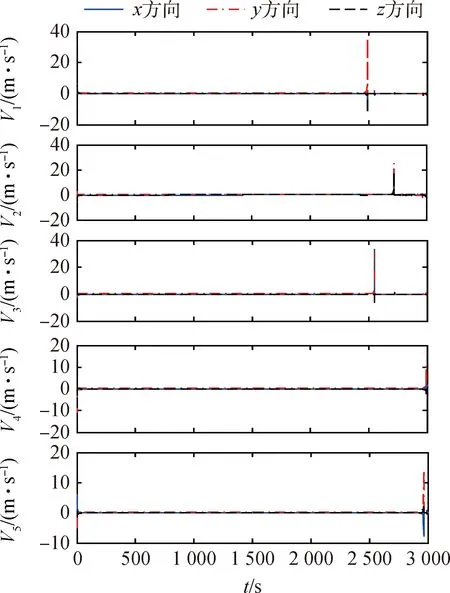
图4 各成员相对非合作目标的速度变化Fig.4 Velocity variation of members relative to the non-cooperative target
通过图4可以看出,编队系统各成员的速度变化经历了内段和外段两个阶段,仿真开始时,各航天器在外段速度场的作用下向目标转移,在约2 400s时各航天器到达期望速度场内段,之后各航天速度发生明显震荡,经短时间调整后,各航天器速度趋近于零。
行为调节参数的选取将对相对运动轨迹产生影响,b越大,碰撞避免权重越大,速度变化越剧烈,所需脉冲速度越大;cj越大,则到达期望位置的时间越短,参数设计时可根据需要进行折中选择。
4 结束语
本文研究了基于行为的空间非合作目标编队飞行轨迹规划算法,将任意时间各航天器的期望速度定义为聚集行为速度、驻留行为速度和避让行为速度的加权和,通过构造平衡态构型公式将轨迹规划转化成行为调节参数的设计问题,调节参数的求解方程组为线性系统,求解过程简单。仿真结果表明,编队系统可在3 000s内运动至期望构型,且避免了成员之间以及成员与非合作目标之间的碰撞。本文提出的算法能够较好解决复杂编队构型的轨迹规划问题,且成员数量越多优势越明显。但是该方法不能完全实现所有可能的构型,构型需要具有对称性,后续工作将针对非对称性编队构型开展算法的改进研究。
References)
[1] 张琪新,孙富春,许斌,等. 基于离散粒子群算法的多飞行器在轨服务任务分配J]. 中国空间科学技术,2012,32(2):68-76.
ZHANG Q X,SUN F C,XU B,et al. Multiple spacecrafts on-orbit service task allocation based on DPSOJ]. Chinese Space Science and Technology,2012,32(2):68-76(in Chinese).
[2] 徐李佳,胡勇. 椭圆轨道非合作目标交会接近策略与控制J]. 中国空间科学技术,2015,35(6):1-11.
XU L J,HU Y. Approach planning and control method for rendezvous with non-cooperative target in an elliptical orbitJ]. Chinese Space Science and Technology,2015,35(6):1-11(in Chinese).
[3] 王辉,顾学迈. 编队卫星防碰撞规避路径规划方法与控制研究J]. 中国空间科学技术,2009,29(5):67-74.
WANG H,GU X M. Autonomous determination of relative orbit for satellite formation flying using radio-only measurementJ]. Chinese Space Science and Technology,2009,29(5):67-74(in Chinese).
[4] 宋申民,张大伟,裴润. 非合作自主交会对接的动态障碍物躲避制导J].中国科学空间技术,2010,30(6):39-47.
SONG S M,ZHANG D W,PEI R. Guidance for dynamic obstacle avoidance of autonomous rendezvous and docking with non-cooperative targetJ]. Chinese Space Science and Technology,2010,30(6):39-47(in Chinese).
[5] 高鹏,罗建军.航天器规避动态障碍物的自适应人工势函数制导J].中国空间技术技术,2012,32(5):1-8.
GAO P,LUO J J. Adaptive artificial potential function guidance of dynamic obstacle avoidance of spacecraftJ]. Chinese Space Science and Technology,2012,32(5):1-8(in Chinese).
[6] 卢山,徐世杰. 非合作目标的自主接近控制律研究J]. 中国空间科学技术,2008,28(5):7-12.
LU S,XU S J. Control laws for autonomous proximity with non-cooperative targetJ]. Chinese Space Science and Technology,2008,28(5):7-12(in Chinese).
[7] BALCH T,ARKIN R C. Behavior-based formation control for multi-robot teamsJ]. IEEE Transactions on Robotics and Automation,1988,14(6):926-939.
[8] DARIO IZZO LORENZO PETTAZZI. Autonomous and Distributed Motion Planning for Satellite SwarmJ]. Journal of Guidance,Control,and Dynamics,2007,30(2):449-459.
[9] 曾志峰,汤一华,陈士橹,等. 基于行为的太阳帆群编队方法J]. 西北工业大学学报,2012,30(1):44-48.
ZENG Z F,TANG Y H,CHEN S L,et al. a better formation planning algorithm of solar sail swarm based on BehaviorJ]. Journal of Northwestern Polytechnical University,2012,20(1):44-48(in Chinese).
(编辑:车晓玲)
Trajectory planning for non-cooperative target multi-spacecraft formation based on behavior strategy
WANG Tao1,2,XU Yongsheng2,ZHANG Yingchun1,2,*,XIE Chengqing2
1.HarbinInstituteofTechnology,Harbin150001,China2.AerospaceDongfanghongDevelopmentLtd.,Shenzhen518057,China
The current spacecraft formation trajectory plannings don′t consider non-cooperative target,configuration complexity and collaborative control problem. A relative motion trajectory planning method based on behavior strategy was proposed for non-cooperative target multi-spacecraft formation system. Firstly,an underlying kinematical field was designed based on the gather model. Expect speed was defined as a series of speed vector with different behavior features. The behavior adjust parameters were calculated by constructing equilibrium shaping formula. Secondly,the non-cooperative target was described with Gauss environment function.The expect kinematical field was improved by using the C-W function. The method not only avoids the collision between the formation members,but also guarantees the safe distance between the non-cooperative targets. The simulation results show that the algorithm can make the multi-spacecraft formation system moving to the expect configuration in 3 000 seconds. The method has obvious advantages when used in complex,multiple control target of the formation system trajectory planning. It is autonomy,collaborative,strong robustness,and etc.At the same time the method can be applied to different types of formation configuration relative motion planning.
behavior strategy;non-cooperative target;multi-spacecraft formation;collision avoidance;trajectory planning
10.16708/j.cnki.1000-758X.2017.0006
2016-10-25;
2017-01-10;录用日期:2017-01-24;
时间:2017-02-16 18:28:12
http:∥www.cnki.net/kcms/detail/11.1859.V.20170216.1828.008.html
国家自然科学基金(61473297);深圳市知识创新计划基础研究项目(JCYJ20140903102802052)
王涛(1986-),男,博士研究生,terry1860@126.com,研究方向为航天器动力学与控制
*通讯作者:张迎春(1961-),男,教授,zhang@hit.edu.cn,研究方向为卫星总体设计技术
王涛,许永生,张迎春,等.基于行为的非合作目标多航天器编队轨迹规划J].中国空间科学技术,2017,37(1):19-25.WANGT,XUYS,ZHANGYC,etal.Trajectoryplanningfornon-cooperativetargetmulti-spacecraftformationbasedonbehaviorstrategyJ].ChineseSpaceScienceandTechnology,2017,37(1):19-25(inChinese).
V412.4
A
http:∥zgkj.cast.cn
