地月自由返回轨道设计
2017-03-30王丹阳邓辉
王丹阳,邓辉
南京大学 天文与空间科学学院,南京 210023
地月自由返回轨道设计
王丹阳*,邓辉
南京大学 天文与空间科学学院,南京 210023
载人月球探测任务需要着重考虑任务的安全性,能否“自由返回”是很重要的一项指标。在轨道设计上存在两项要求,首先是地月转移,然后是经月球近旁转向并判断能否返回地球,即实现飞越月球以后的无动力返回。文章结合精确的行星历表(DE405),首先比较不同力模型中同一条轨道的返回情况,以确定初始轨道设计过程中需要考虑的摄动力;然后分析了返回时近地距的各种影响因素,包括出发时刻、转移时间、倾角组合等,提出了一种可使返回近地距逐渐向设定的目标值靠拢的单向搜索方法,该方法简单易行,可信度高,能够满足轨道设计时要求的各项约束条件。该工作对中国将要进行的载人月球探测任务中需要用到的自由返回轨道的设计具有一定的参考价值。
自由返回轨道;力模型;返回近地距;影响因素;地球端倾角范围
嫦娥三号探测器的发射成功,说明中国无人软着陆月球探测技术的成熟,这是月球探测的重要一步,为接下来的载人探测任务奠定了基础。
在轨道设计时,载人探测任务要求探测器在近月点变轨时如果发生动力故障,经月球转向后可以返回地球1]。典型例子是阿波罗13号探测器,其出现动力故障以后借助自由返回轨道安全返回,被称为是“一次成功的失败”2]。对于这种轨道,文献3]从平面圆型限制性三体问题出发,研究了白道面内的自由转移轨道特征,然后推广到三维情形,不足之处是需要预先设置近月点。文献4]给出了双二体模型下自由返回轨道的设计方法,并使用二分法搜索影响返回的变量,文献5]通过引入优化算法提高了搜索的效率,不足之处是约束条件部分单薄。文献6]对自由返回轨道的特性进行了分析。以上文献多采用拼接法,对拼接法而言,近月点高度不是约束条件之一7-8],只要在一定范围内就认为满足条件,而载人登月需要在月球附近建立环月停泊轨道,近月点高度应该是固定的。本文采用固定近月点高度,改变其他约束条件的搜索策略设计自由返回轨道。
地月自由返回轨道设计的第一步是地月转移轨道,关于地月转移轨道的设计可以参考文献9],基本思路是采用双二体拼接方法,先赋初值然后微分修正至满足约束条件,这一过程在这里不作详细介绍。
1 坐标系与运动方程
DE405星历表采用的坐标系为国际天球参考系(ICRS),与历元J2000.0平赤道系差别很小,一般可认为二者等价。在地心J2000.0平赤道坐标系中,探测器需要满足的比较完整的力模型为
(1)
式中:rmp=rep-rem,rsp=rep-res,rem,res由DE405历表给出;μe,μm,μs分别是地球、月球、太阳的引力常数;as,ap分别是光压、七大行星的摄动,这里不考虑地、月的非球形引力、潮汐、大气等。对于限制性四体模型,只需要考虑前三项。本文在探讨发射窗口的问题时还涉及日地旋转坐标系(见图1),由于地月转移时间3d左右,这段时间地球只公转过很小的角度,不再进行转换。月心段轨道采用J2000.0月心平赤道系(坐标原点移至月心,坐标轴平行)。
光压的表达式为
(2)
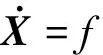
(3)
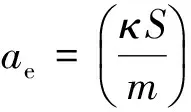
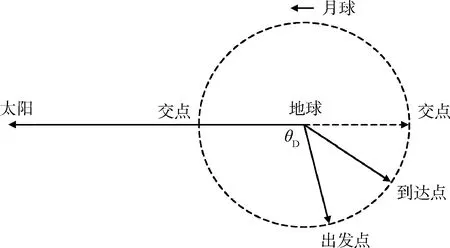
图1 日地旋转坐标系中天体构形示意Fig.1 Illustration of celestial bodies configuration in Sun-Earth rotating frame
2 不同模型中返回情况的比较
第三体摄动的表达式为
(4)
式中:r′为由天体指向探测器的距离矢量;rei为该天体的地心坐标。设探测器的地心坐标为r,探测器—地球—第三体夹角为θ。
(5)
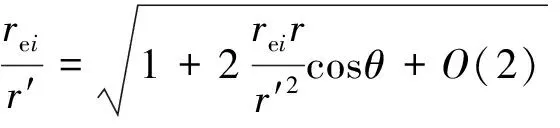
(6)
(7)
当θ=0°或180°时,
(8)
摄动量级
(9)
对地月转移轨道,r不超过地月距离,如果取为3.8×105km,对于太阳摄动(μs/μe≈332 946)该比值约为1.08×10-2。而考虑其他行星的摄动时,如木星的摄动(μj/μe≈317.9),木地最近距离近似取4AU,该比值为8×10-8,充分说明行星摄动很小。关于第三体摄动的具体影响,下面的数值计算也可以说明问题。同一条轨道在各种力模型中的返回近地距如表1所示。
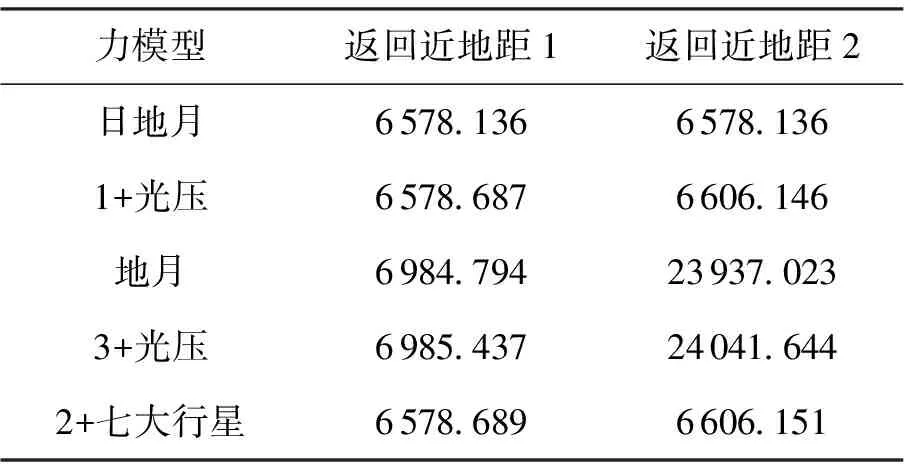
表1 同一条轨道在各种力模型中的返回近地距
这里同一条轨道是指出发时刻简化儒略日MJD=58 162.3,转移时间3.494 31d,两端倾角分别为140°、157°,近地(月)点高度200km,升轨出发、降轨到达,这些约束条件都相同。返回近地距1是由不同的力模型经过微分修正迭代出不同的初值在相应的力模型中外推给出的结果,限制性四体模型与最后一项较为完整的力模型给出的结果相差非常小,说明对于初始轨道设计采用限制性四体模型是合理的。返回近地距2是由限制性四体模型迭代出的相同的初值在不同的力模型中外推得到的结果,纵向比较说明太阳引力的影响很大,太阳光压的影响在数十千米的量级。两列结果同时说明的问题是地月系中的探测器不需要考虑太阳系中其他行星的影响。下面的计算中将采用力模型1(限制性四体模型),即只考虑日、地、月的质点引力并忽略探测器质量。
3 轨道设计方法与特征分析
3.1 轨道需要满足的约束条件
首先是地月转移,约束条件为
(10)
式中:re,rm为地球、月球半径;h1,h2,ii,i2为近地(月)点高度、倾角,对于停泊轨道h1=200 km。
自由返回轨道需要在此基础上增加约束条件,假设在近月点发动机故障没有变轨继续向前飞行,经过足够长的时间t在第一次靠近地球时到达环绕轨道高度或者更近的距离,最终利用大气减速降落到地面,增加的约束条件为
(11)
取等号表示返回高度为h3的环绕轨道(一般仍为200km高度的停泊轨道),近地点有两种计算方法,一是通过二分法判断,因为近地点恰好是位置速度内积为零的分界点;二是程序中每步都计算地心距记录最小值(大范围搜索时适用),这里采用RKF7(8)自适应步长积分器,截断误差设置为1D-10(10-10)。
自由返回轨道的设计总的来说是一个搜索的过程,不断变动影响rmin(t)的变量,搜索出满足条件的变量组合。由于影响因素较多,这里先固定转移时间,然后在搜索到的返回时近地点距离在目标值附近处通过微调转移时间使得近地点距离满足约束条件,找到自由返回轨道,具体流程见图2,eps表示可接受的距离误差,dev取1 000km。
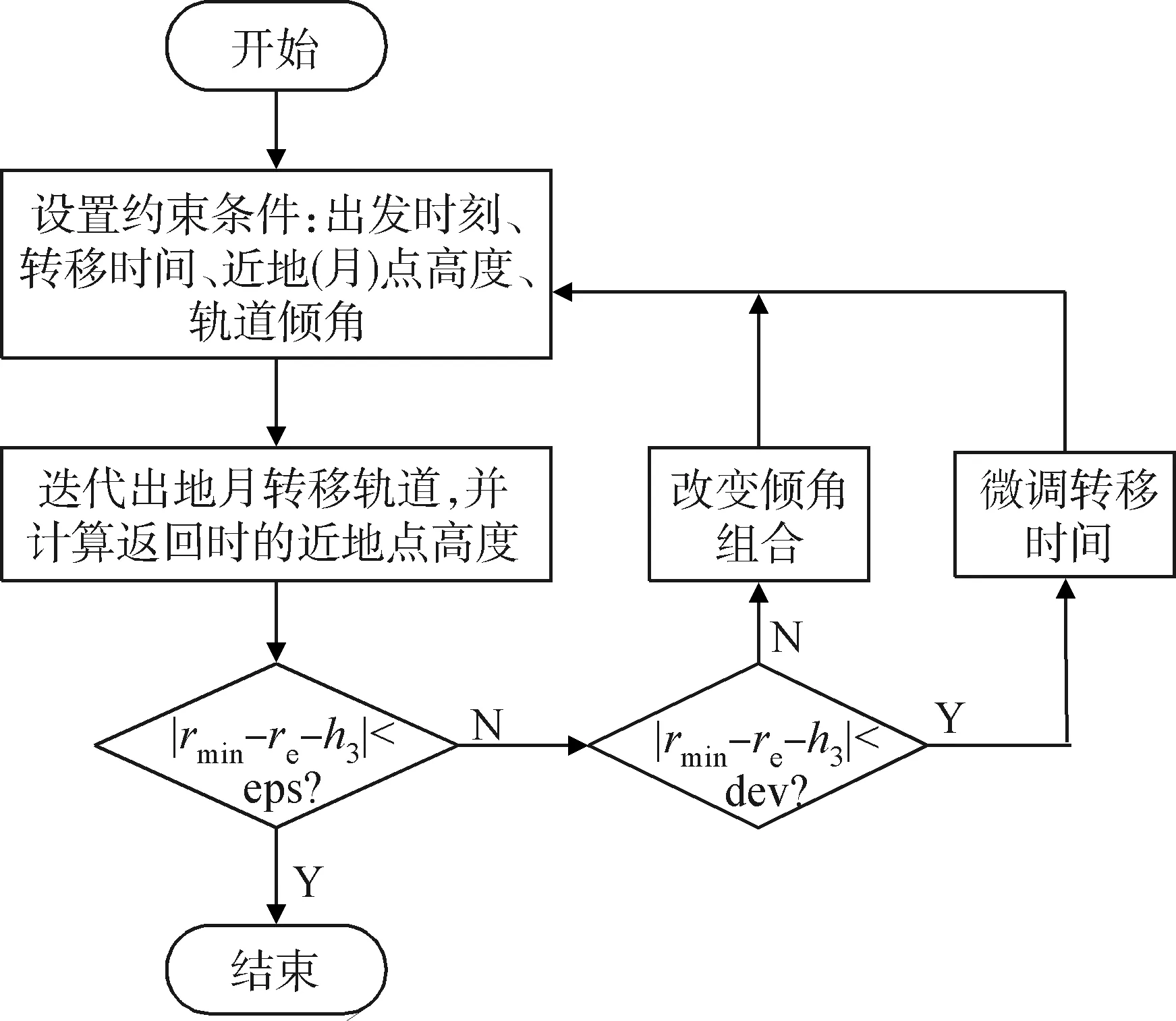
图2 地月自由返回轨道设计流程Fig.2 Flowchat of cislunar free return trajectory design
3.2 影响返回时近地点距离的因素
对返回时近地点距离有影响的因素就是设计地月转移轨道时的各项约束条件:近地(月)点幅角(升、降轨),地月两端倾角,近地(月)点高度,出发时刻和转移时间这几项,最终的返回时近地点距离是这几个变量综合作用的结果。一般来讲,近地(月)点高度应设置为停泊轨道高度为固定值,考虑到实现起来的困难地月两端倾角的设定最好是整数值。出发时刻的差别主要在于月球处在公转轨道上的位置不同,具有周期性特征。考虑到两脉冲转移的能量消耗,转移时间不能太小(小于3.0d)。下面将对上述几种影响因素做具体分析。
(1)近地(月)点幅角的影响分析
对于决定升、降轨转移方式的近地(月)点幅角,相同的约束条件不同的ω初值一般会收敛到两种不同的升、降轨转移方式上,但也有收敛到两条同为升、降轨转移方式的情况(两个ω所属区间相同),这是非常有意思的事情。两种出发方式,两种到达方式,返回时的近地点高度并不相同,意味着同一时刻有4种不同的返回距离。如果能够固定升、降轨出发方式,则降至2种返回距离,搜索时采用不同的赋初值方式得到2个可行的ω来“叠加”出某一时刻返回时的最小近地点距离。
这里以一个算例说明近地(月)点幅角、地月两端倾角、近月点高度对最终结果的影响。
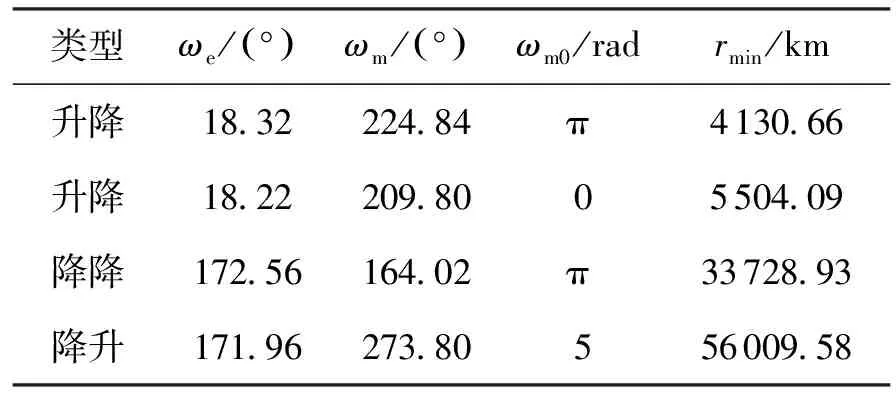
表2 4种转移方式对应的返回近地距
出发时刻为MJD=58 163.3,转移时间3.5d,地月两端的倾角分别为141°、157°。同一出发时刻,相同的转移时间,总是存在4条不同的转移轨道,并且这4条轨道的返回近地距差别很大。
(2)轨道倾角、近月点高度的影响分析
仍然采用上述算例,并采用升轨出发,降轨到达的初值设定(近月点幅角初值为π)。以此为基础,分别变更地月两端倾角、近月点高度得到图3和图4。
图3中地球端倾角变化范围140°~150°,月球端倾角变化范围154°~157°,最小近地点距离对应(141°,157°)这一组合。从图3可以看出返回时近地点距离对转移轨道地月两端的倾角变化非常敏感,月球端倾角差1°返回时近地距相差数千千米,地球端倾角差1°返回时近地距相差数百千米。返回时近地点距离与转移时间的关系如图5所示。
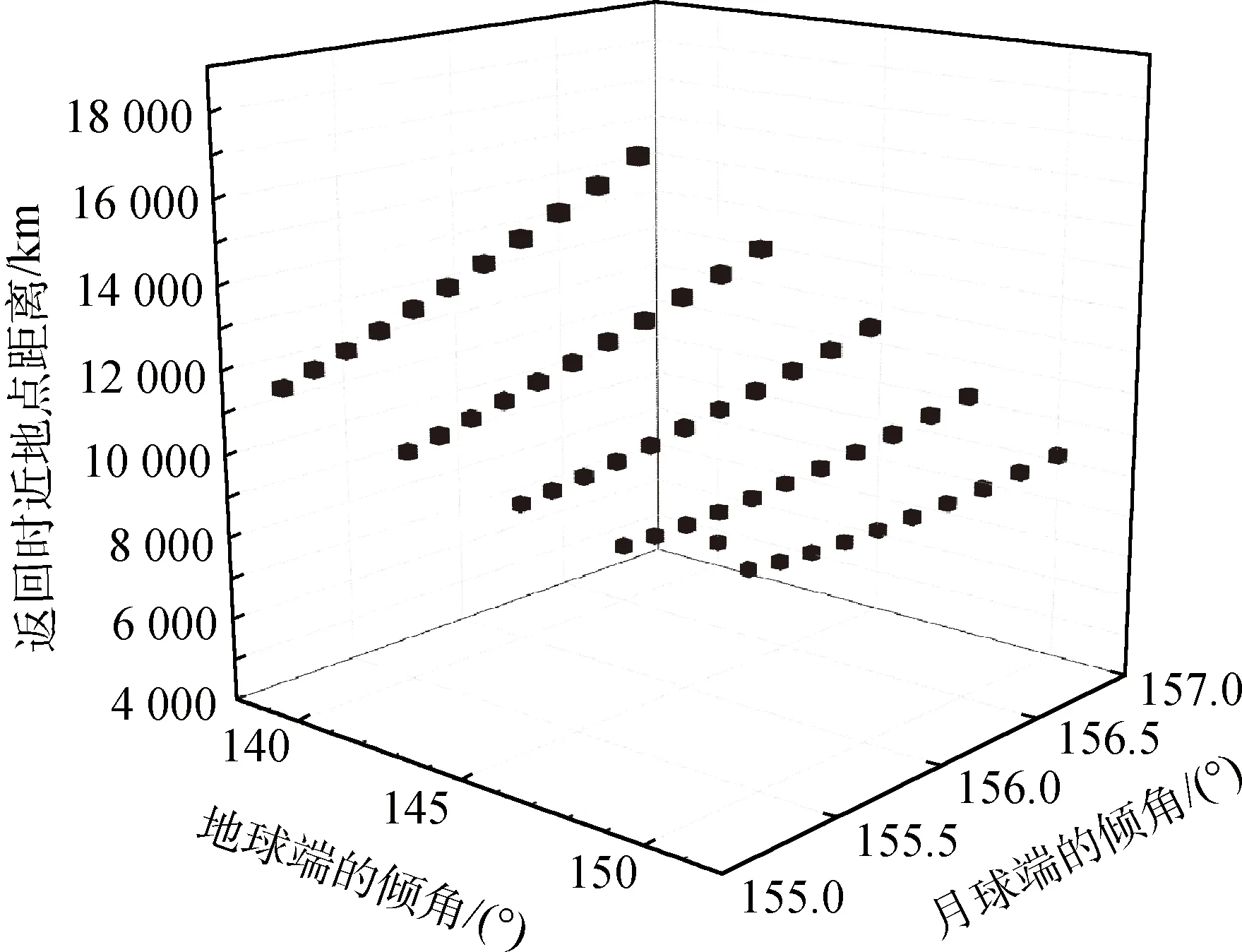
图3 返回时近地点距离与两端倾角的关系Fig.3 Relation between return perigee distances and inclination angles in both sides
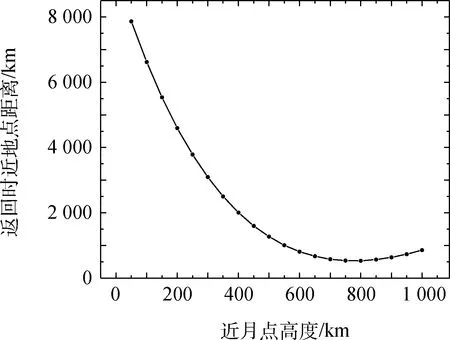
图4 返回时近地点距离与近月点高度的关系Fig.4 Relation between return perigee distances and heights of perilune

图5 返回时近地点距离与转移时间的关系Fig.5 Relation between return perigee distances and transfer time
(3)出发时刻、转移时间的影响分析
这里出发时刻都是指从停泊轨道奔月时的变轨时刻,转移时间是指从近地点到达近月点的时间。由于需要考虑月球位置的影响,以下算例中显示的时刻是到达近月点的时刻,出发时刻需要减去转移时间。相同的到达近月点时刻,返回近地距与转移时间关系见图5(约束条件同前),由该图可知在其他条件都相同的情况下,仅通过改变转移时间和出发时刻,存在两条自由返回轨道。需要说明的是,在某一时刻自由返回轨道成立的组合条件并不适用于另外一个时刻,原因主要是由于月球位置的不同,影响到地球端出发时的轨道倾角。所以从停泊轨道出发,在不同出发时刻自由返回轨道是否总是存在就是一个需要验证的问题。
对这个问题,这里采用在一定时间范围内搜索自由返回轨道的验证方式,具体搜索过程为:将近地、月点轨道高度都设为200km,到达近月点的转移时间为3.5d,到达近月点时刻从2018年2月15日19时开始(MJD=58 164.8,白赤交角约20°,日地月夹角约0°)搜索60d内飞越月球以后返回时的近地距,地球端均采用升轨出发,出发时倾角30°~150°,步长10°;月球端到达时的倾角搜索范围分为两个阶段,首先是大步长全局搜索,这时会发现可以实现自由返回的倾角范围很小;然后在该范围中采用小步长局域搜索,150°~165°、步长1°,搜索的目标是当前时刻存在的最小近地距离,只要该距离小于6 578km就存在自由返回轨道。
60d内出发时刻搜索步长为0.5d,该过程给出的结果如图6所示,图6中的4幅图分别对应不同的近月点幅角初值ω0(不同的初值会迭代到不同的ω,同一时刻同样的出发方式存在两个满足约束条件的值,当ω∈π/2,3π/2)时表示降轨,其余为升轨),图中两个相邻的峰(谷)值相差27.5d。
图7是由图6下面两幅图合并而成,返回时近地点距离满足停泊轨道高度的就是自由返回轨道,并且任一时刻只要最小距离小于该值自由返回轨道就一定存在。从图7中看出这种轨道的存在是分时间段的(横线以下的时间段)。
总体而言,转移时间为3.5d的自由返回轨道比较少,以至于最初认为其是周期性存在的。但实际上,当把转移时间缩减以后得到的结果会发生显著变化,图8是转移时间为3.2d的情况。
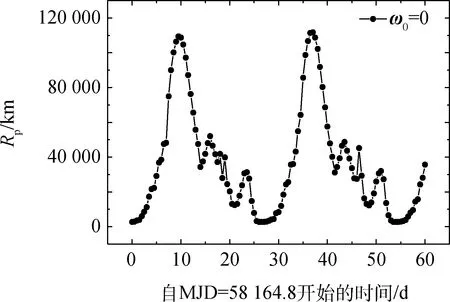
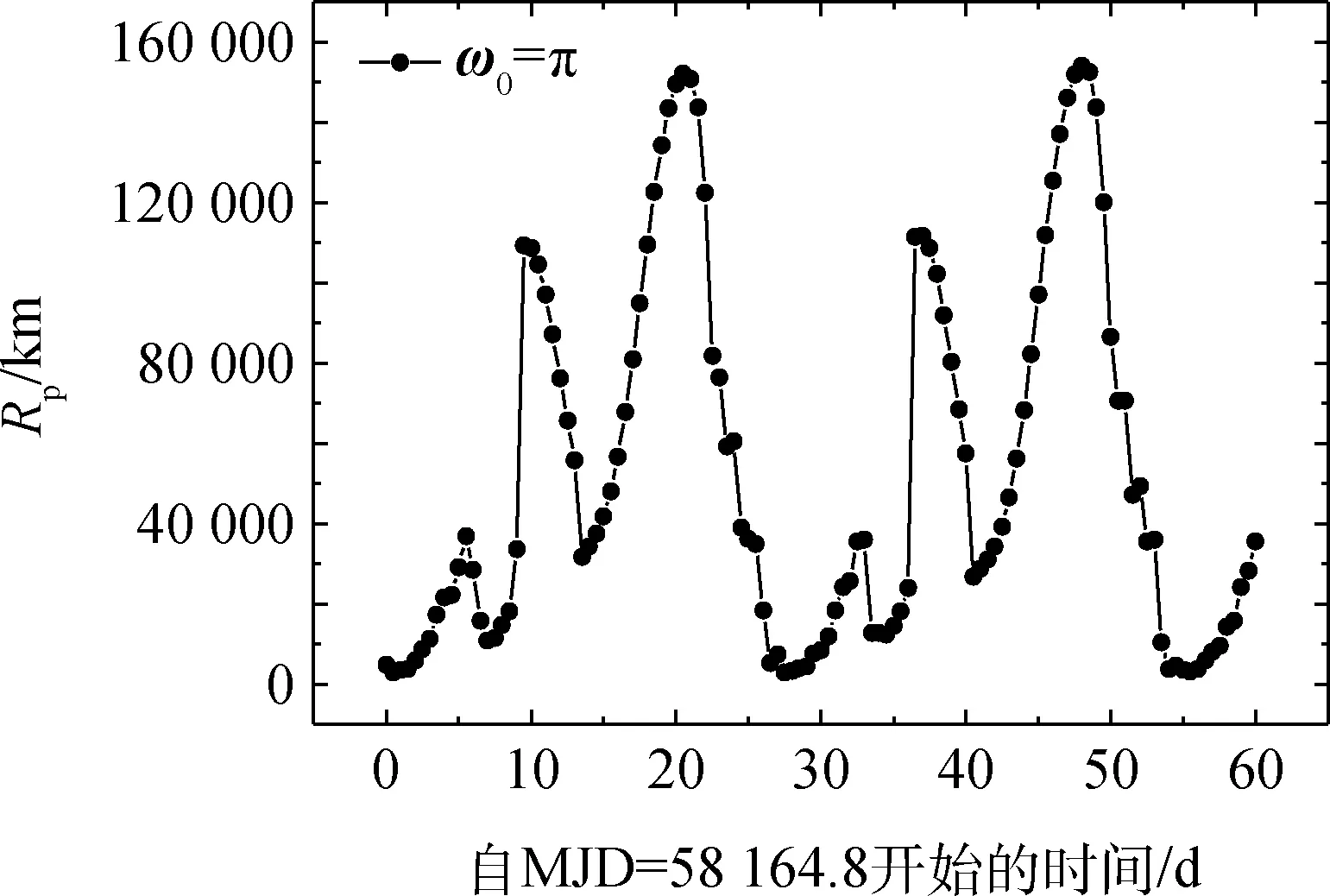
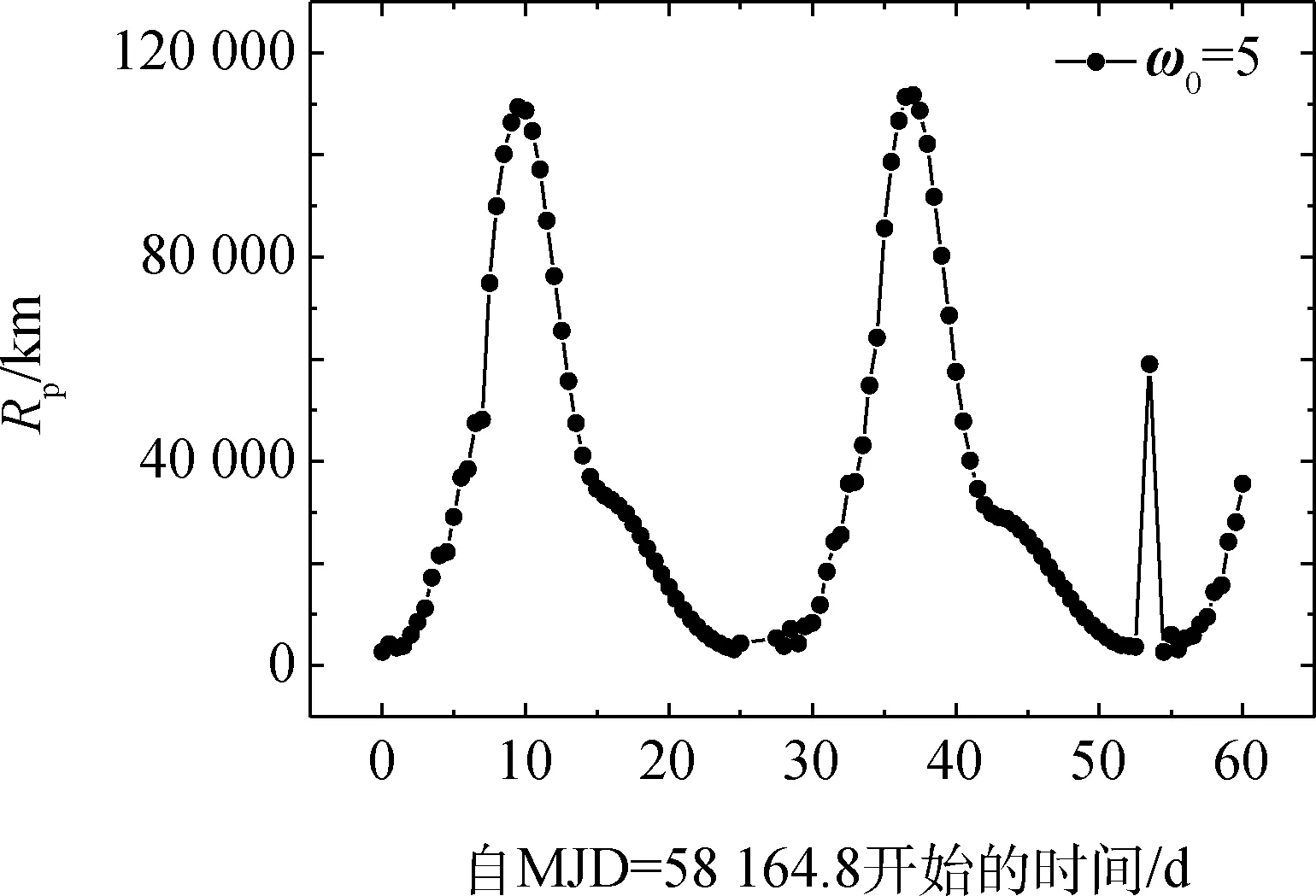
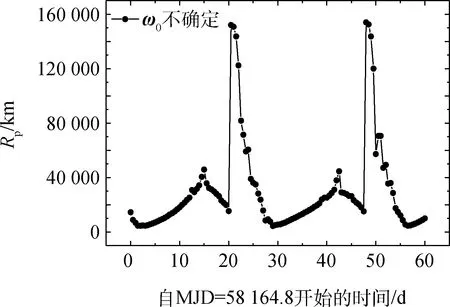
图6 不同近月点幅角初值在60 d内飞越月球以后返回时的最小近地点距离Fig.6 Min return perigee distances with lunar swing-by in 60 days with different initial argument of perilune
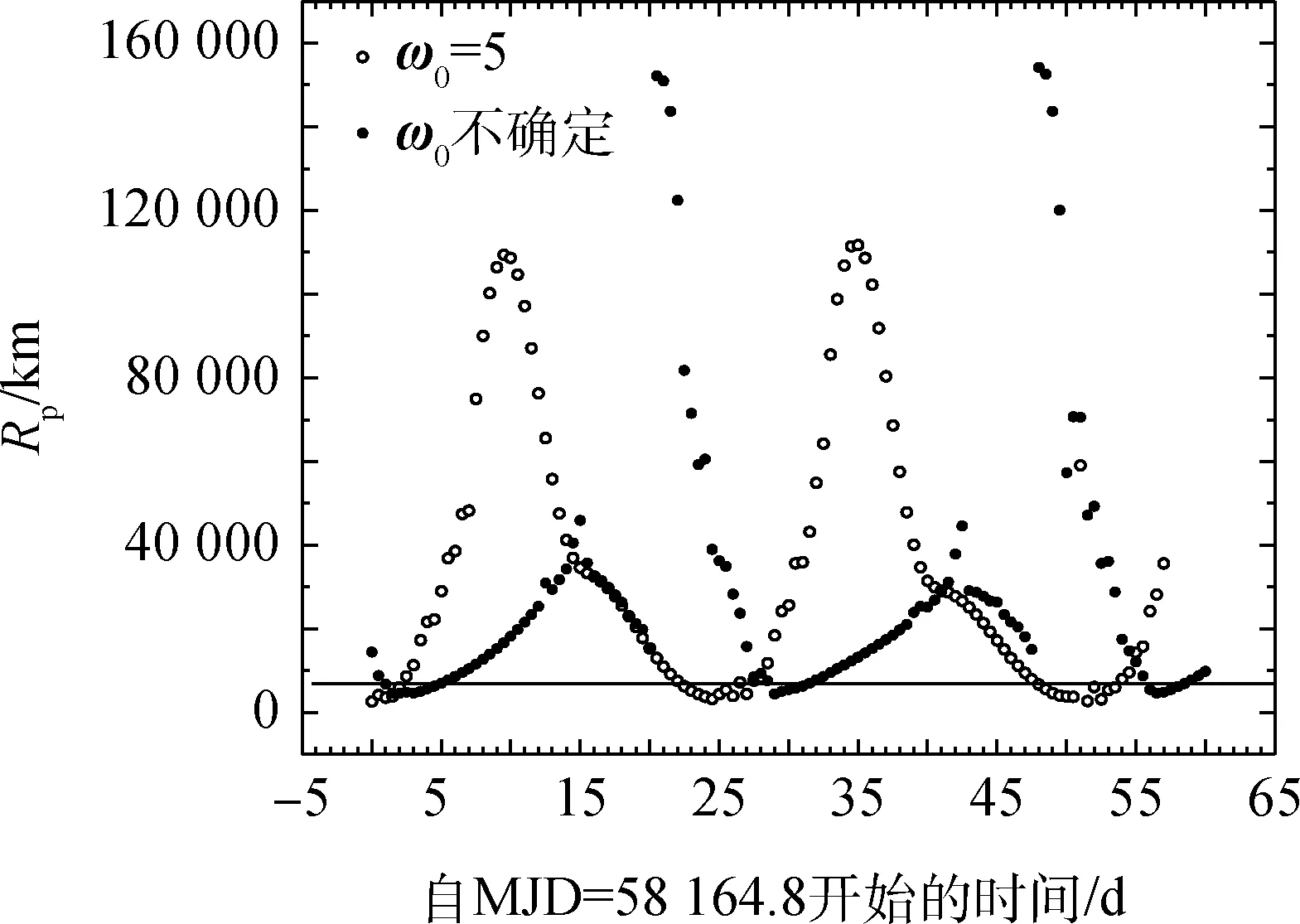
图7 转移时间为3.5 d的返回时最小近地距Fig.7 Minimum return perigee distances with 3.5 days transfer time
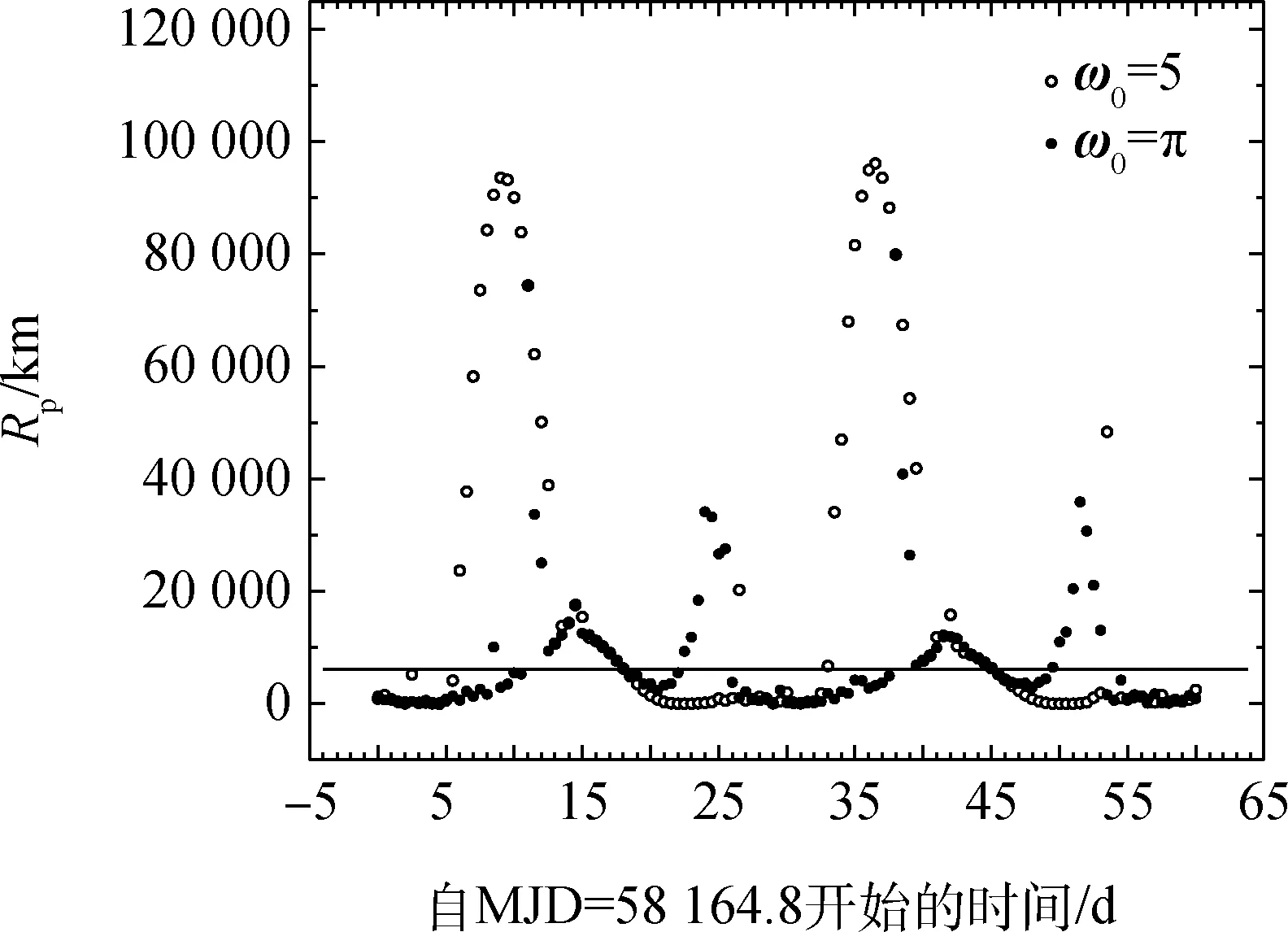
图8 转移时间为3.2 d的返回时最小近地距Fig.8 Minimum return perigee distances with 3.2 days transfer time
月球的公转轨道面(白道面)与地心天球坐标系的平赤道面有两个交点,图7、图8中的局部高点(两条线取较小值)处于第14.5d、42.0d这两个时刻,经历表分析,这时月球处于公转轨道的降交点附近。两图同时出现的现象是当月球处于降交点位置时,在其他条件都相同时返回近地距会偏大,这是升轨出发的一个现象。
转移时间对返回近地距的影响是显著的,转移时间为3.2d的自由返回轨道要明显多于3.5d的。同时相同转移时间的返回近地距离具有周期性,该周期非常接近月球的公转周期27.5d,说明返回近地点距离与月球的位置有关系。下面对30d范围内的返回情况进行了更多计算(与前面不同的是采用降轨出发),结果如图9所示。图9中3.0d、3.1d的图像说明从停泊轨道出发,自由返回轨道始终存在,这是非常好的结果。而当转移时间逐渐变长以后,自由返回轨道周期性存在,再变长估计就不存在了,这里不去考察转移时间很长的情况。
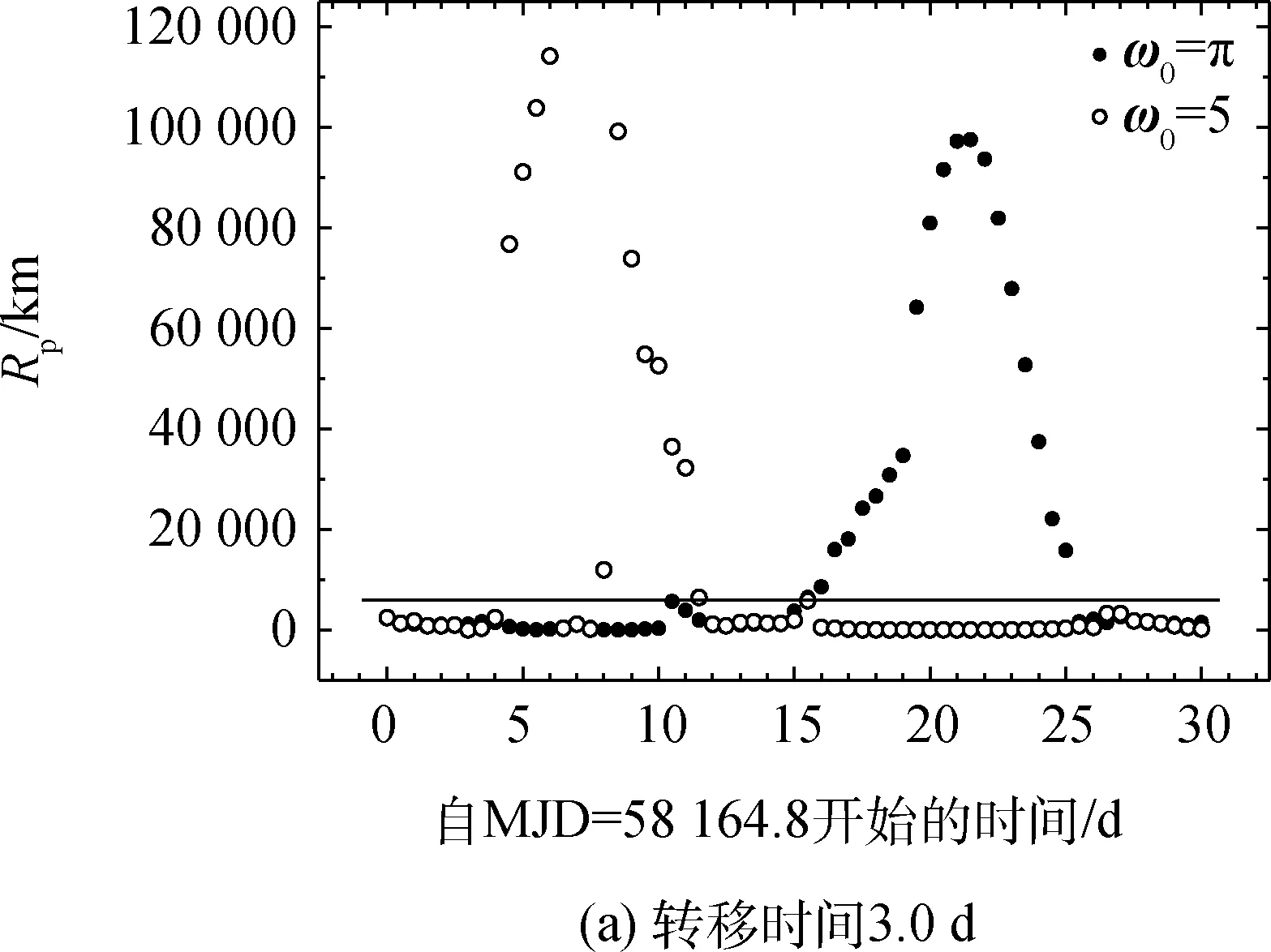
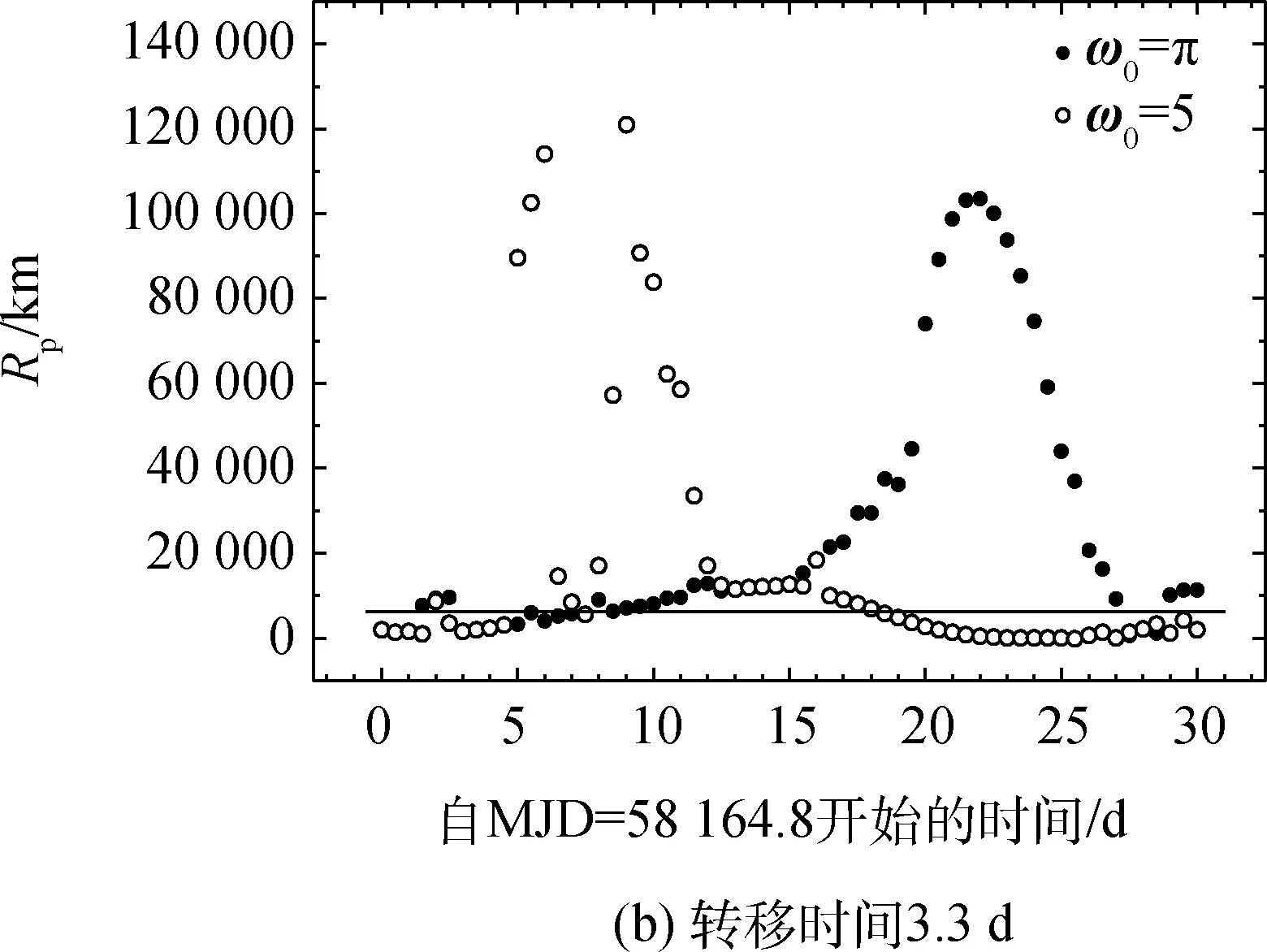
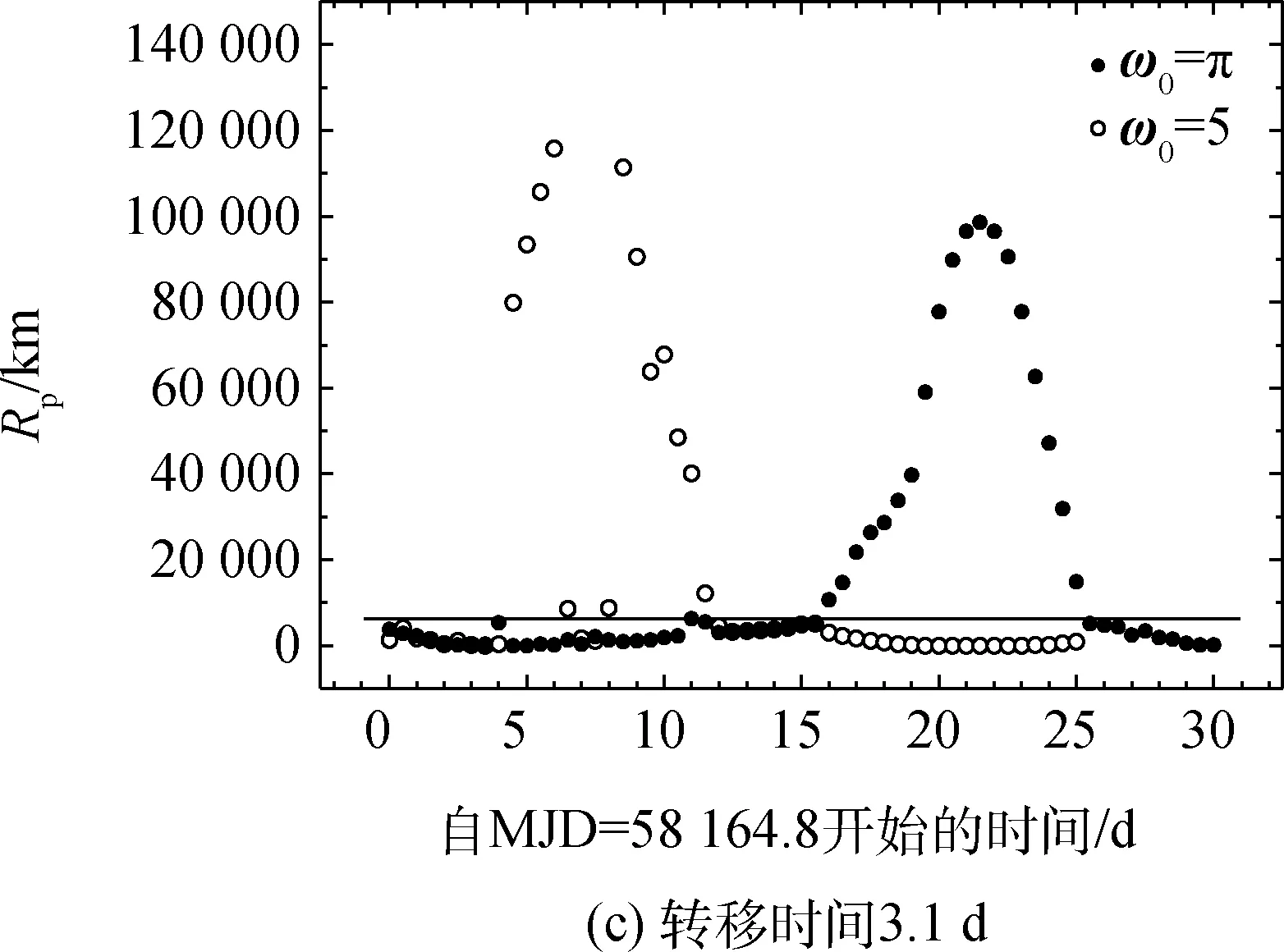
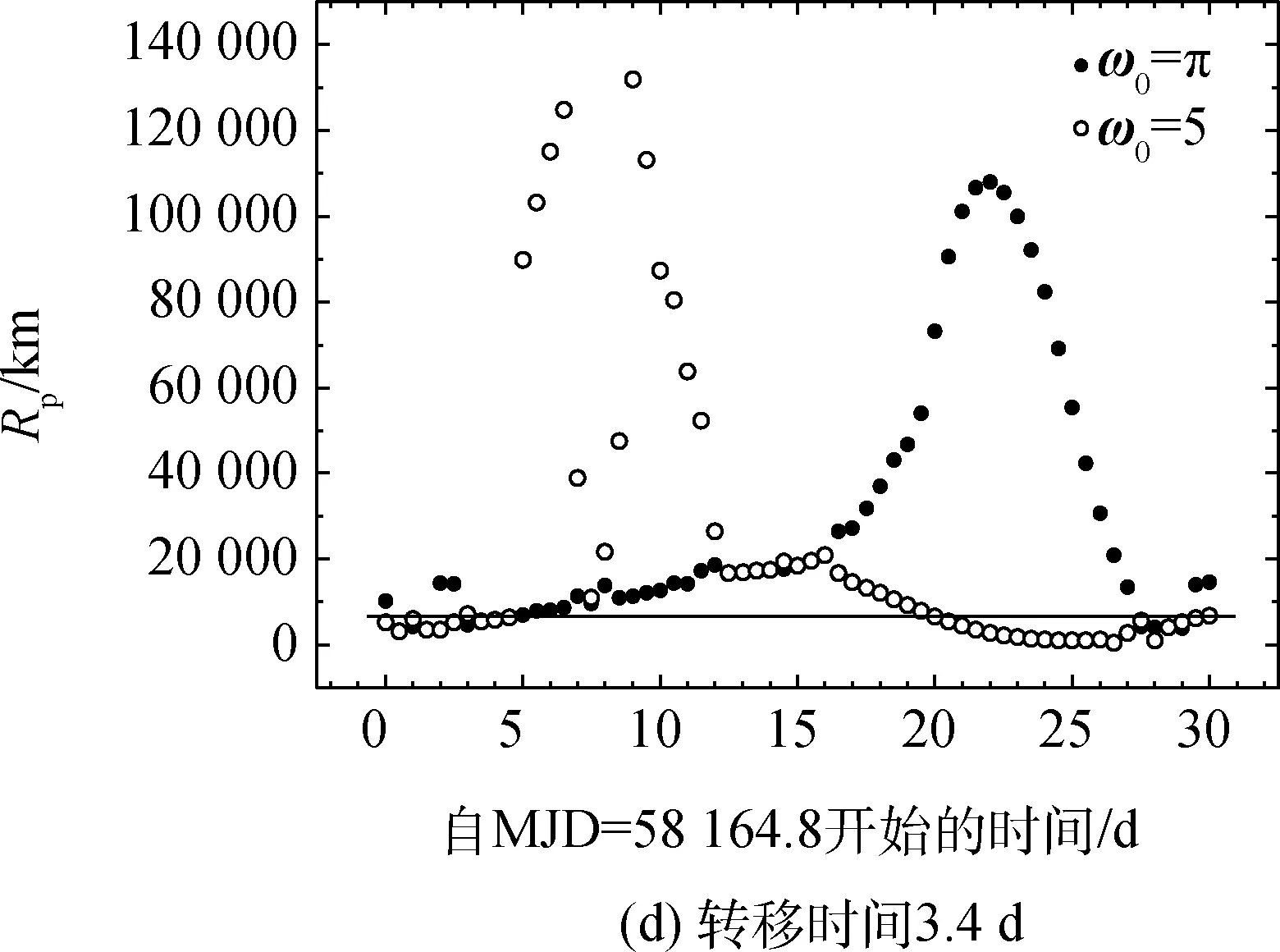
图9 不同转移时间返回时的最小近地距Fig.9 Min return perigee distances with different transfer time
需要说明的是,虽然转移时间短有利于自由返回轨道的存在,但同时也伴随着两脉冲能量消耗的增大(在本文计算的时间范围内会有数十米/秒的差别),这是地月转移轨道的能量特征,是容易理解的。所以这里也不去考察3.0d以下的转移时间,因为能量消耗会显著增加。
3.3 不同出发时刻地球端的倾角范围
本文在转移轨道设计时已设定从停泊轨道切向变轨,出发时地球端的转移轨道倾角就是停泊轨道的倾角。考虑到发射场因素,停泊轨道的倾角(超过90°时取其补角)不能小于发射场的纬度(原因与月球公转位置对地球端出发倾角的约束是相同的),所以有必要分析自由返回轨道在地球端的倾角范围。这里将转移时间初值设定为3.1d,按照自由返回轨道设计流程图在进入微调转移时间阶段记录地球端的倾角,将搜索步长降至1°(该过程非常耗时),得到图10。
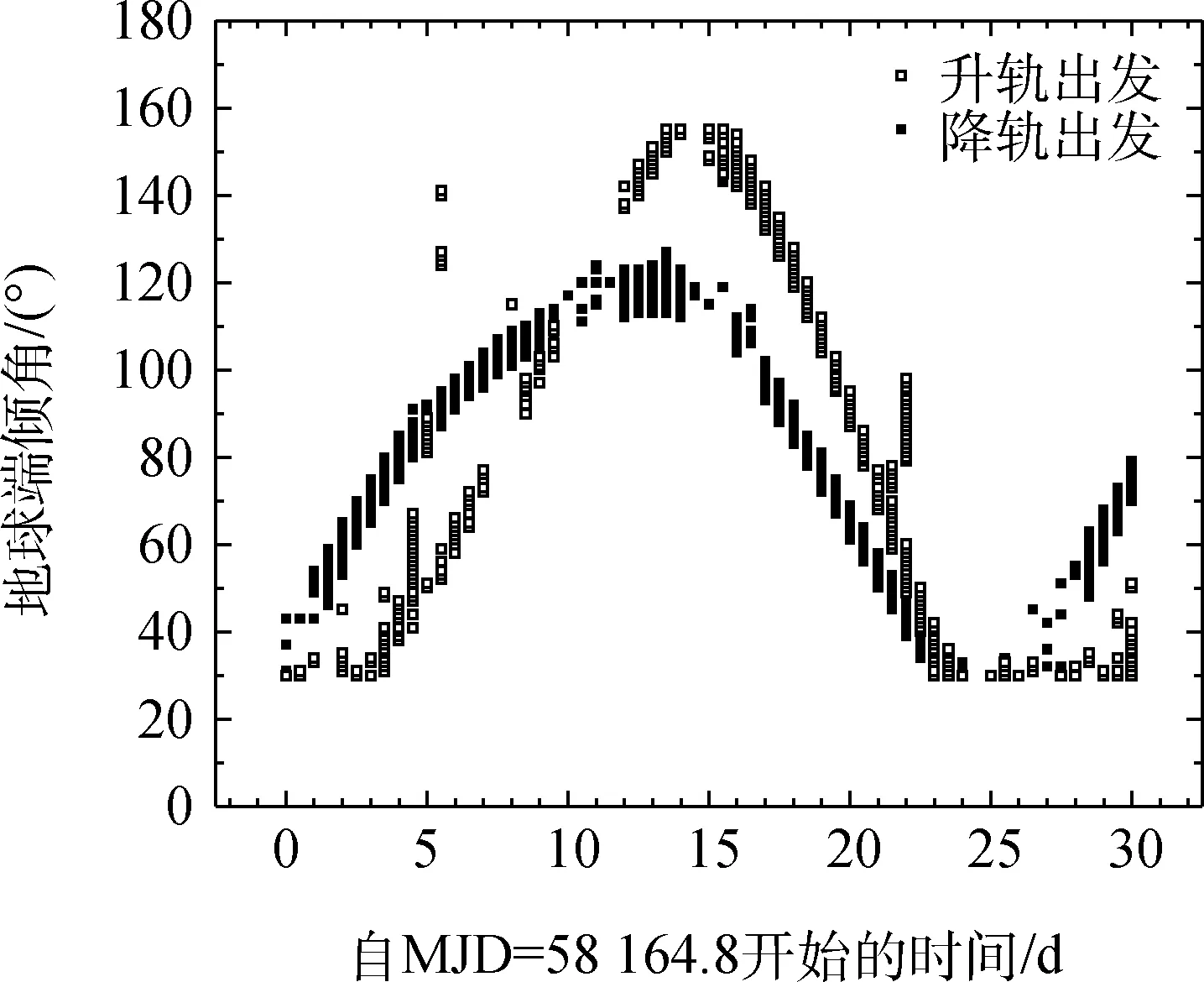
图10 转移时间在3.1 d附近的自由返回轨道地球端倾角范围Fig.10 Inclination angles near the earth of free return trajectories with about 3.1 days transfer time
图10的结果说明自由返回轨道对探测器在地球附近变轨时的轨道倾角范围并没有非常严格的要求,是在一个非常宽泛的区间内变化,这说明理论上来讲地月自由返回轨道对发射场的纬度因素几乎没有选择性,只要选择合适的出发时刻,几乎所有的发射场都有发射机会,只不过低纬度发射场这样的机会更多一些而已。
3.4 地月自由返回轨道的图像
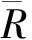
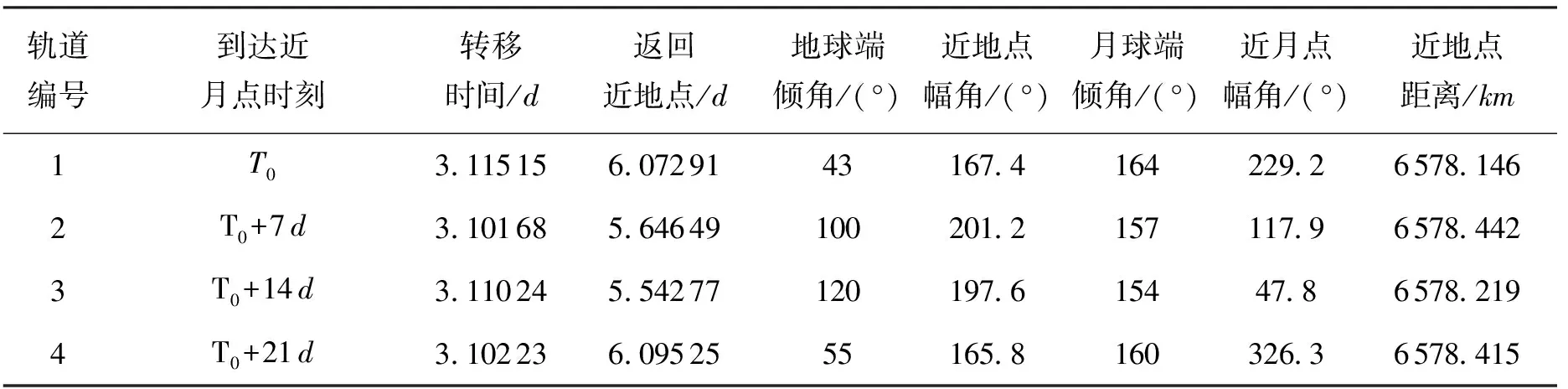
表3 4条地月自由返回轨道的具体参数
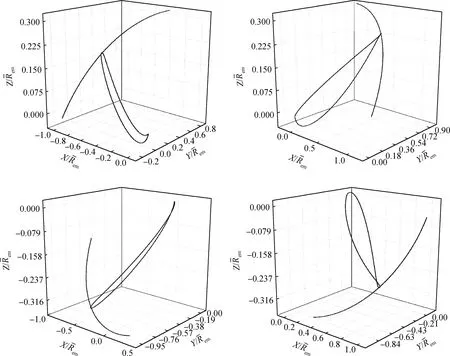
图11 4条地月自由返回轨道Fig.11 Orbit graphics of four cislunar free return trajectories
4 结束语
本文探讨了近月点高度固定的自由返回轨道的搜索方法,该方法在地月转移时间初值设置合理时通过改变地月两端倾角约束可以给出多个使得返回近地距在目标值附近的倾角组合,然后通过微调转移时间最终确定自由返回轨道。由于返回近地距在目标值附近对转移时间的变化是单调的,微调转移时间搜索自由返回轨道这一过程是比较容易的,意味着该方法切实可行。
References)
[1] 郗晓宁,黄文德,王威. 载人登月任务中止轨道问题综述J]. 中国科学:技术科学, 2011,41(5): 537-544.
XI X N, HUANG W D, WANG W. Review on abort trajectory for manned lunar landing missionJ]. Sci.China Tech.Sci., 2011, 41(5):537-544(in Chinese).
[2] KAUFFMAN J. A successful failure: NASA′s crisis communications regarding Apollo 13J]. Public Relations Review, 2001, 27(4): 437-448.
[3] 侯锡云,赵玉晖,刘林. 月球探测中的无动力返回轨道J]. 天文学报, 2012, 53(4): 308-318.
HOU X Y, ZHAO Y H, LIU L. Free return trajectories in lunar MissionsJ]. Chinese Astronomy & Astrophysics,2012,53(4):308-318(in Chinese).
[4] 黄文德,郗晓宁,王威,等. 基于二体假设的载人登月自由返回轨道特性分析及设计J]. 宇航学报, 2010, 31(5): 1297-1303.
HUANG W D, XI X N, WANG W,et al.Characteristic analysis and design of free return orbit for lunar manned landing based on the double two-body modelJ]. Journal of Astronautics, 2010, 31(5): 1297-1303(in Chinese).
[5] 彭祺擘,沈红新,李海阳. 载人登月自由返回轨道设计及特性分析J]. 中国科学:技术科学, 2012, 42(3): 333-341.
PENG Q B, SHEN H X, LI H Y. Free return orbit design and characteristics analysis for manned lunar missionJ]. Sci.China Tech.Sci., 2012, 42(3):333-341(in Chinese).
[6] 张磊,于登云,张熇. 绕月自由返回轨道的设计与分析J]. 航天器工程, 2010, 19(2): 128-135.
ZHANG L, YU D Y, ZHANG H. Design and analysis of circumlunar free-return orbitsJ]. Spacecraft Engineering, 2010, 19(2):128-135(in Chinese).
[7] WILSON R S,HOWELL K C. Trajectory design in the Sun-Earth-Moon system using lunar gravity assistsJ]. Journal of Spacecraft & Rockets, 2015, 35(35):191-198.
[8] FARQUHAR R W,DUNHAM D W.A new trajectory concept for exploring the Earth′s geomagnetic tailJ]. Journal of Guidance Control and Dynamics, 1981, 4(2): 192-196.
[9] 刘林,王歆. 月球探测器轨道力学M]. 北京:国防工业出版社,2006:15-50.
LIU L, WANG X. Orbital mechanics of lunar probeM]. Beijing: National Defence Industry Press, 2006:15-50(in Chinese).
(编辑:高珍)
Cislunar free return trajectory design
WANG Danyang*,DENG Hui
SchoolofAstronomyandSpaceScience,NanjingUniversity,Nanjing210023,China
The most important thing in manned lunar explorations is safety, whether the probe can free return when facing power failure at the perilune is an important criterion. With the aim of designing cislunar free return trajectory, two requirements should be satisfied, the first is transfer trajectory design between the earth and moon, the second is whether the probe can fly back after lunar swing-by. Combined with the precise astronomical ephemeris (DE405),one trajectory in different mechanical models was compared in order to determine what perturbations should be considered in the preliminary trajectory design. Then, almost all factors (departure time, transfer time, inclination angles combination, etc.) affecting the return perigee distance of the probe was analyzed.A unidirectional search method was proposed,which could make the probe′s return perigee distance tend to the set target value gradually. The method is simple and reliable, and it can satisfy all the requirements of initial trajectory design. The work is of some value to the cislunar free return trajectory design of our manned lunar explorations in the near future.
free return trajectory; mechanical models; return perigee distance;influencing factors; inclination angle range around the earth
10.16708/j.cnki.1000-758X.2017.0013
2016-06-18;
2016-09-06;录用日期:2017-01-24;
时间:2017-02-16 18:16:13
http:∥www.cnki.net/kcms/detail/11.1859.V.20170216.1816.006.html
国家自然科学基金(11322330)
王丹阳,邓辉. 地月自由返回轨道设计J].中国空间科学技术,2017,37(1):57-65.WANGDY,DENGH.CislunarfreereturntrajectorydesignJ].ChineseSpaceScienceandTechnology,2017,37(1):57-65(inChinese).
V476.3
A
http:∥zgkj.cast.cn
*通讯作者:王丹阳(1990-),男,硕士研究生,wdy@smail.nju.edu.cn,研究方向为深空探测轨道设计
