基于自适应迭代学习的小行星绕飞容错控制
2017-03-30黄怡欣李爽江秀强
黄怡欣,李爽,*,江秀强
1.南京航空航天大学 航天学院,南京 210016 2.南京航空航天大学 航天新技术实验室,南京 210016
基于自适应迭代学习的小行星绕飞容错控制
黄怡欣1,2,李爽1,2,*,江秀强1,2
1.南京航空航天大学 航天学院,南京 210016 2.南京航空航天大学 航天新技术实验室,南京 210016
对于小行星绕飞任务的探测器姿态控制问题,已有方法大都考虑了干扰力矩和参数不确定等因素,而忽视了执行器故障情况。针对执行器故障条件下的小行星探测器姿态控制问题,提出了一种基于自适应迭代学习的容错控制方法。所设计的控制器包括两部分:其一针对执行器故障,设计了自适应迭代学习控制器,采用类滑模的思想和自适应迭代学习算法对控制器参数进行调整,进而补偿执行器故障带来的影响,保证系统在控制输出不足情况下的高精度姿态稳定性;其二针对探测器参量变化、外部环境干扰等不确定情况,设计了基于自适应神经网络的迭代学习控制器,采用径向基函数(Radial Basis Function,RBF)神经网络对系统非线性部分进行逼近,同时对控制器参数进行自适应迭代学习调整,进而保证系统在不确定情况下的动态性能。数值仿真结果表明该控制器能够有效抑制外部环境干扰和内部参数变化带来的不利影响,在执行器部分失效甚至完全失效故障情况下,仍能保证系统的鲁棒性并实现误差在10-2数量级内的较高姿态控制精度。
小行星探测器;容错控制;自适应迭代学习;神经网络;执行器故障
小行星探测有助于人类了解太阳系的起源和演化,并为危险近地小行星防御技术的研究与验证提供了重要途径1]。为了获取小行星准确的几何外形、尺寸和质量分布等特征参数,一般需要探测器在距小行星数万米的圆轨道或者椭圆轨道上进行数十天的绕飞探测1-2]。这就要求探测器的姿态控制系统能够保证有效载荷稳定地指向小行星表面,同时还要满足天线对地定向和太阳电池阵对日定向的要求。但由于小行星本身尺寸较小、形状和质量分布不规则而造成不规则的弱引力场,加之其他邻近大、小行星的引力及太阳光压等摄动力的影响,使得小行星附近的力学环境十分复杂,也给探测器的精确姿态控制带来了严峻的挑战3-7]。此外,小行星探测器在长期的星际航行过程中极有可能出现执行器故障,这必将使得问题进一步恶化。
截至目前,国内外学者对小行星探测器姿态控制问题的研究大都没有考虑执行器故障的情况。针对小行星引力不规则和太阳光压的影响,文献8]采用反馈线性化设计了姿态控制律,保证小行星绕飞探测器在摄动影响下的姿态稳定性。文献9]针对433小行星Eros绕飞任务,将摄动力矩视为外部干扰,利用李雅普诺夫方法设计了反馈控制律,进而保证探测器的姿态稳定性。除了外界的摄动因素,小行星探测器自身执行器故障也是实际任务中难以避免的另一大问题,该问题轻则影响探测器的控制性能,重则导致整个探测任务的失败。
近年来,迭代学习控制算法以其高精度的控制特点,受到了广泛的研究和关注。已有学者将迭代学习算法应用到航天器姿态控制和编队飞行中,并取得了良好的控制效果10-12]。采用迭代学习算法进行姿态控制能够有效地抑制控制过程中出现的重复性干扰,并具有较高的控制精度。而将自适应算法引入迭代学习控制,用控制参数的迭代而不是控制律本身的迭代进行设计,能够在保证控制精度的同时简化控制器设计13-15]。针对带有执行器故障而导致控制输出不足问题的探测任务,本文采用自适应迭代学习算法抑制绕飞过程中的重复性干扰,并补偿执行器故障所造成的不利影响,同时加入自适应神经网络对系统不确定项进行逼近,以增强探测器姿态控制的鲁棒性和可靠性,为后续探测器容错控制研究打下良好基础。
1 小行星探测器姿态控制问题描述
1.1 坐标系定义
为了后续描述方便,首先定义需要用到的坐标系:
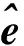
(1)
1.2 球谐函数引力场模型
由于采用球谐函数表达的引力势能和引力场有明确的解析表达式和较高的精度,因此采用小行星的球谐函数引力势能模型16]:
(2)
式中:μ=Gma为小行星的引力系数,ma为小行星质量;Rc为探测器质心到小行星质心的距离;λ和δ分别为探测器所处的经度和纬度;r0为小行星的参考半径;N和i分别为系统的展开阶数和次数;Pijsin(δ)为sin(δ)的缔合勒让德多项式;Cij和Sij为球谐系数(由小行星质量分布决定)。以Eros433小行星为例,由于引力系数高阶项的影响非常小,通常只需选取作用较大的引力系数项(C20和C22),则小行星引力势能函数可以写成如下形式:
(3)
式(3)中的球坐标与位置矢量Rc=x,y,z]T之间的转换关系为Rc=‖Rc‖,sinδ=z/Rc,tanλ=y/x,因此代入式(3)可得:
(4)
1.3 不规则引力力矩
在小行星附近进行绕飞时,不规则引力力矩会引起探测器姿态发生变化3],探测器上任一质点dm受到小行星的引力为9]:
(5)
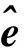
(6)
于是,施加在探测器上的引力力矩为:
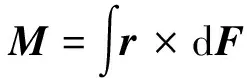
(7)
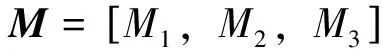
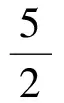
(8)
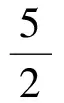
(9)
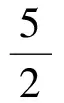
(10)
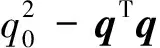
(11)
(12)
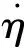
1.4 姿态运动学和动力学方程
用ω∈3表示当前探测器本体坐标系相对于惯性坐标系的旋转角速度,ωd∈3为目标姿态相对于惯性坐标系的旋转角速度,则角速度误差可以表示为ωe=ω-C(Qe)ωd。
姿态跟踪运动学和动力学方程可以写成:
(13)
(14)
(15)
式中:u=u1,u2,u3]T∈3为作用于探测器3个本体轴上的控制力矩矢量;M∈3为小行星引力力矩矢量;Td∈3为太阳光压、太阳引力等干扰合力矩;d∈3为目标角加速度;上标×为斜对称矩阵。
1.5 故障模型
小行星探测器通常采用喷气推力器和反作用飞轮进行姿态控制。在小行星绕飞段,则主要由飞轮进行姿态调整。其出现故障主要表现为以下两种情况:
1)部分失效故障:执行器实际输出值小于控制器指令值;
2)完全失效故障:执行器不输出或被关闭。
设执行器安装矩阵为B∈3×N,并用D(t)表示执行器的健康程度。当出现部分失效故障时有0<δi<1,当执行器完全失效时有δi=0,i=1,2,…,N。
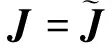
通过上述分析,可将执行器控制性能下降模型写成以下形式:
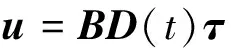
(16)
式中:τ=τ1,τ2,…,τN]T∈N为执行器指令力矩矢量。
将式(16)带入式(15)则得到:
(17)
式中:
(18)
为系统不确定项。
2 控制器设计
本小节分别针对:1)探测器外部干扰和内部参数变化等不确定性因素,2)执行器故障问题,引入自适应迭代学习算法对控制器进行设计,如图1所示。
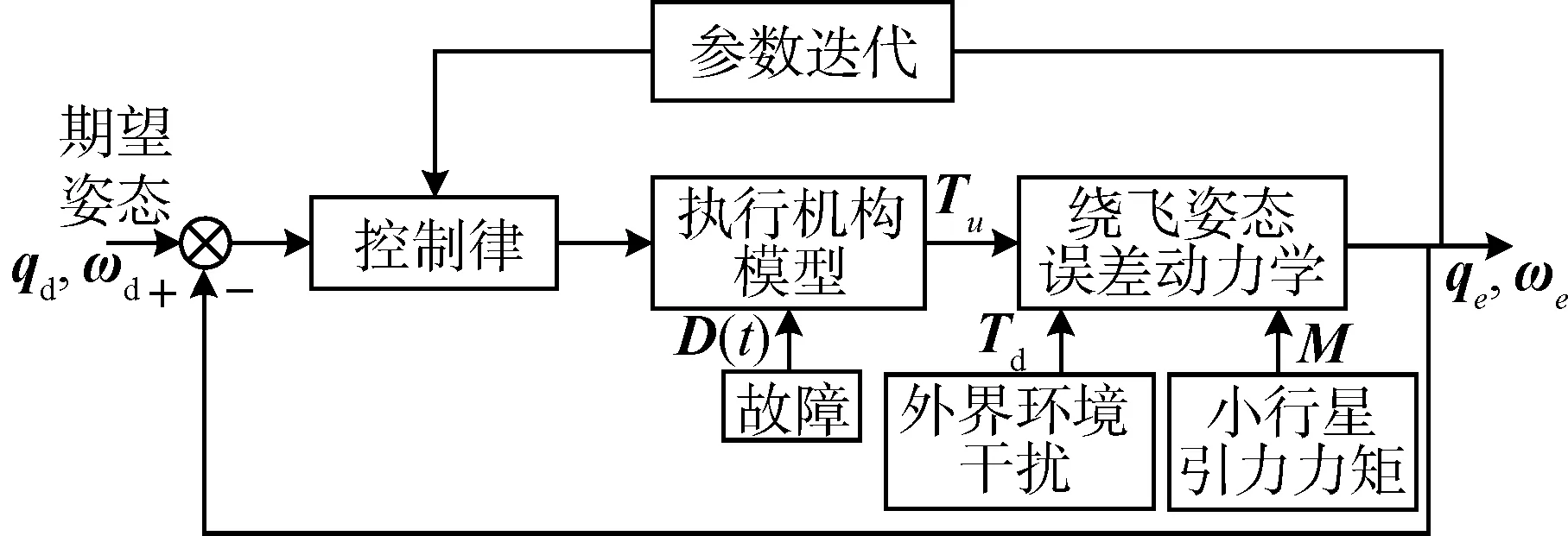
图1 探测器姿态控制系统结构Fig.1 Attitude control system diagram
假设当前为第k次循环,则自适应迭代学习算法的步骤可以简述为:
第一步:将第k-1次循环得到的角速度误差、四元数误差信息进行相关计算,得到总的误差。
第二步:将第k-1次循环的误差量带入第k次循环的控制器设计中,计算出本次循环的控制输出。
第三步:将控制量输入到第k次循环的姿态误差动力学中。
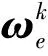
接下来进行具体控制器的设计,首先,定义基本误差函数为:
(19)
式中:c1为待定实参。
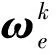
(20)
(21)
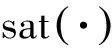
考虑到探测器绕飞过程中的不确定性和执行器故障两方面的问题,控制器的设计分为两个部分:
(22)
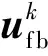
2.1 自适应神经网络补偿控制
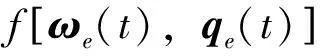
RBF神经网络具有三层网络结构:输入层、隐含层和输出层。输入层到隐含层实现非线性映射,隐含层到输出层实现线性映射。一般的输入层到输出层总的关系式可以表达成:
(23)
式中:y为神经网路的输出;w为输出层连接权重;x为神经网络输入;c为基函数的中心向量;φ为高斯(Gaussian)基函数表示如下:
(24)
式中:σi为一个可以自由选取的参数,它决定了该高斯基函数围绕中心点的宽度。
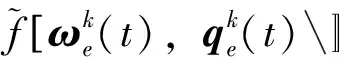
(25)
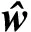
(26)
(27)
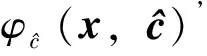
相应的补偿控制器设计如下:
(28)
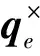
(29)
式中:β1为设计参数;‖·‖表示2范数。
2.2 鲁棒学习控制器
由于探测器在执行绕飞探测时,受各种干扰力矩的影响,需要准确而稳定地姿态控制。为了尽可能地避免因执行器故障而造成姿态失控,使姿态控制系统在故障发生时能够自动补偿故障的影响,维持姿态控制的基本品质,并尽可能地恢复到最佳性能,从而保证姿态控制系统的可靠性。本文将类滑模的思想引入到控制器设计中,得到如下的鲁棒学习控制器:
(30)
式中:θk(t)为迭代参数,并有参数自适应调整律为:
(31)
式中:β2为设计参数。
图2为参数迭代的示意,具体的数值运算参考式(29)和(31),可以看出控制器的迭代仅限于参数迭代,假如当前为第k次控制周期,则控制律中参数θk(t)、ψk(t)与k-1次控制周期的输出有关。参数的迭代而非控制器本身的迭代一定程度上简化了控制器的设计。
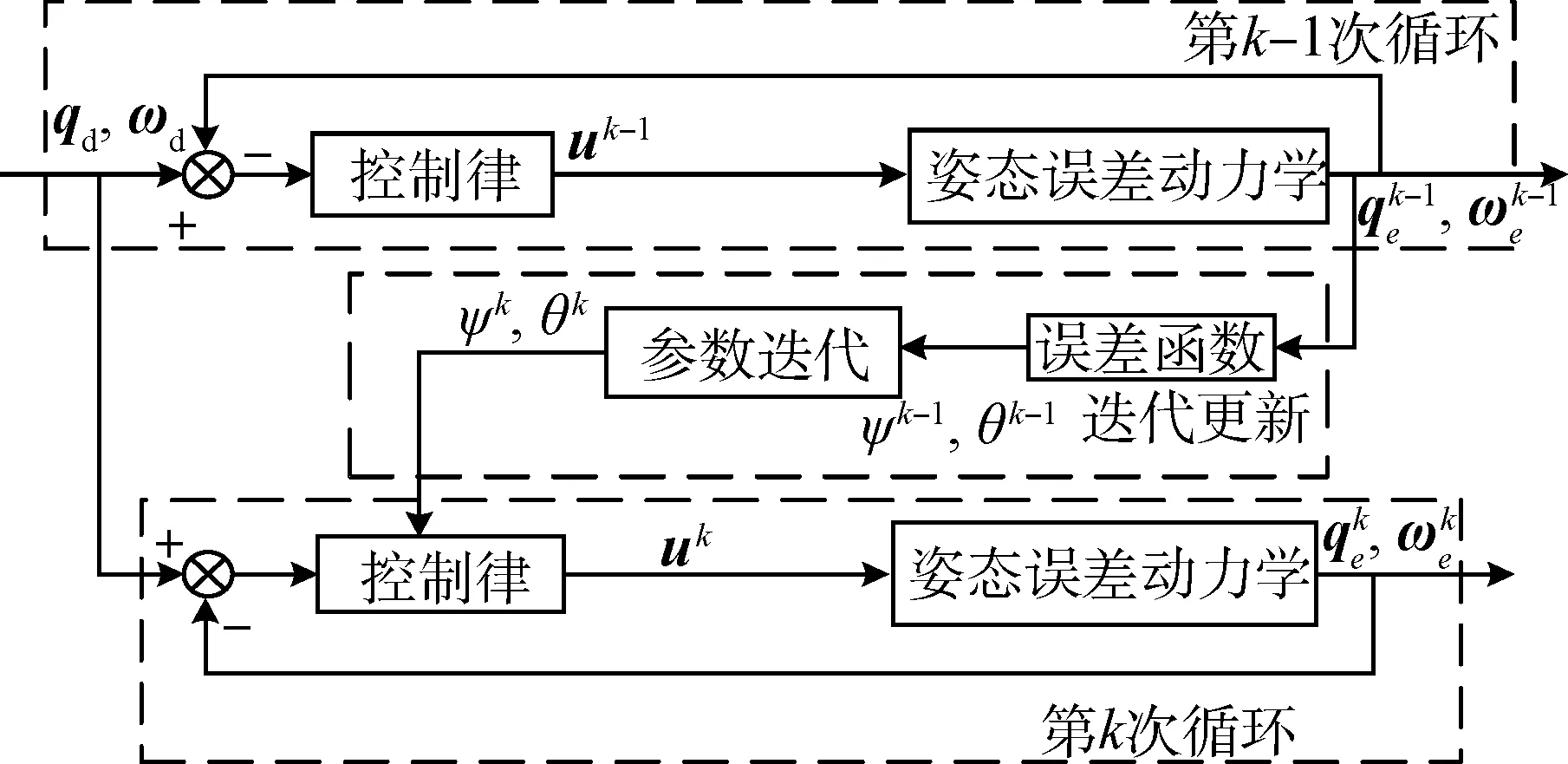
图2 控制律迭代示意Fig.2 Controller iteration diagram
3 稳定性分析
假设:
1)控制输出系数项满足‖J-1‖≥b*>0,b*为常值;
2)角速度误差ωe和姿态误差qe都是可测的。
针对第k次循环,定义Lyapunov方程如下:
(32)
证明:
将Lyapunov方程式(32)对时间求导,得到:
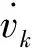
(33)
将式(22)、(28)和(30)控制量uk(t)带入式(33),经过相应化简,有:
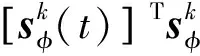
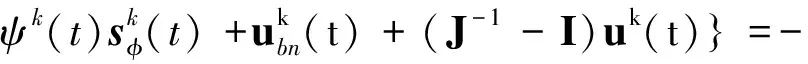
(34)
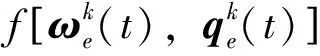
(35)
定义迭代参数ψk(t)和θk(t)的初始值分别为ψ0(t)=ε*,θ0(t)=1/‖J-1‖。考虑到式(29)、(31)的参数自适应律,当定义式中参数β1,β2为正常值时,可以得到迭代参数为单调递增,并始终为正值,则有:
(36)
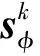
(37)
从而可得式(35)为:
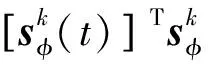
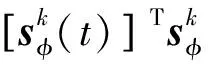
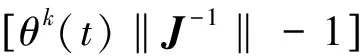
(38)
即证明在第k次迭代时,系统是稳定的。
4 收敛性分析
第3节证明了在第k次迭代中系统是稳定的,这里来分析逐次之间的收敛性。针对k-1次迭代,式(32)Lyapunov方程可以改写如下:
(39)
将式(33)与式(39)相减,得到误差方程:
(40)
(41)
所以,Δvk(t)为非增函数,进而可以证明,当limk→,每次迭代的误差值(t)都会较上一次迭代的误差值(t)更小或者不变。
5 仿真结果与分析
为了验证本文中所设计自适应迭代学习容错控制方法的有效性,将其应用于某型探测器进行仿真分析。以小行星绕飞控制为潜在的工程应用背景,在MATLAB/simulink环境下对本文所提出的方法进行仿真分析。具体的仿真分析场景包括了探测器绕飞无故障情形和有故障情形。表1包括探测器主要参数和控制器仿真参数,表2为小行星相关参数。

表1 探测器主要仿真参数
本文仿真分析中执行器采用3正装1斜装的反作用飞轮,配置矩阵B的表达式为:
探测器在绕飞段除了受到小行星不规则引力干扰作用外,还受到由于太阳引力、太阳光压引起的扰动力矩等重复性干扰,由分析可知19-20],这类干扰可以用下面的正弦函数进行模拟,即式(15)中的Td有:

表2 小行星(Eros 433)参数
控制器参数选取如下:c1=0.2,η=3,ψ0(0)=0.1,θ0(0)=0.01,β1=2,β2=3,κw=1,κc=1,λw=0.5,λc=0.03,α1=0.1,α2=0.05。
5.1 无控制作用下探测器姿态
当无控制作用在探测器上时,即式(15)中控制输入Tu=0,可得到无控制作用下绕飞段探测器姿态误差四元数仿真曲线如图3所示。
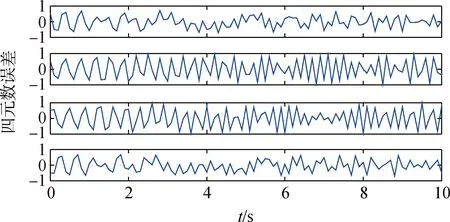
图3 无控制作用时四元数误差Fig.3 Quaternion errors for uncontrolled rotational motion
图3显示出在小行星绕飞段,无控制作用下的探测器姿态,由于小行星本体和太阳所带来的摄动力干扰而呈现周期性的误差。这将会对观测任务带来较大影响。
5.2 无故障情形

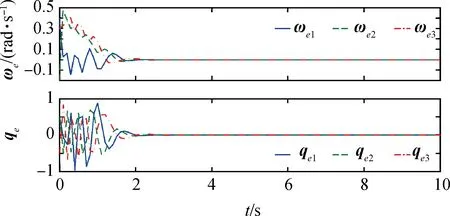
图4 无故障情形下四元数与角速度误差(1次参数迭代后)Fig.4 Quaternion and angular velocity errors for no failure motion(first iteration)
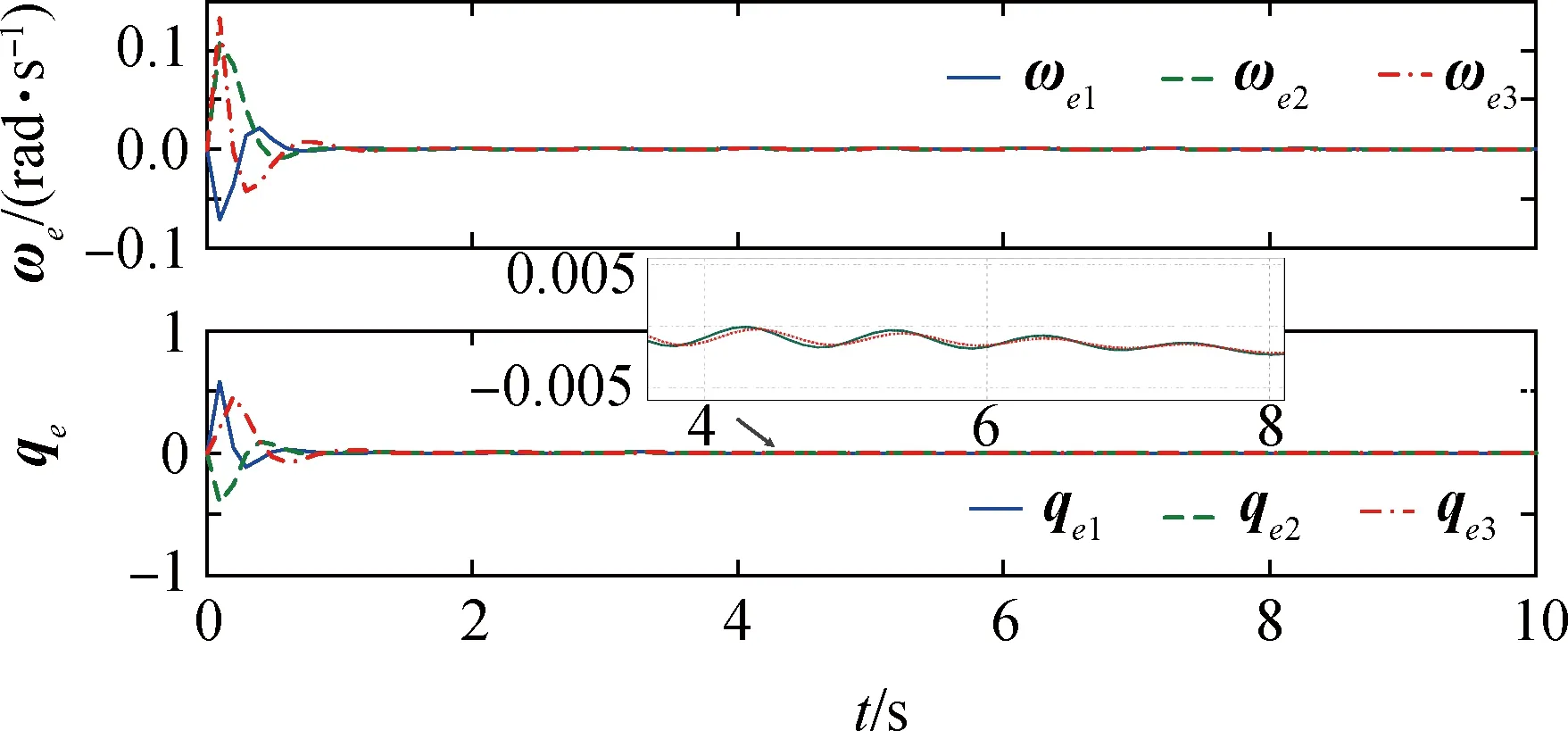
图5 无故障情形下四元数与角速度误差(4次参数迭代后)Fig.5 Quaternion and angular velocity errors for no failure motion (forth iteration)
无故障情形下系统仅受到了摄动力干扰和自身参量不确定性的影响,此时主要由神经网络补偿控制部分起作用。由图4可以看出,由于干扰和参量变化影响,第1次参数迭代后四元数误差和角速度误差大概在3s后收敛。而由图5可以看出,经过4次参数迭代后四元数误差能够在第2s内收敛,同时角速度误差初期的震荡现象明显削弱。这说明本文所设计的控制器能够在摄动力干扰、自身参量不确定性情况下,保证探测器姿态高精度的收敛性,甚至是有限时间内的收敛。
5.3 部分失效故障情形


为了进一步验证本文设计的自适应迭代学习容错控制器的有效性和可行性,本节在执行器失效故障模式下进行了仿真。系统从第0.2s出现部分执行器失效故障,故障补偿控制器开始作用,同时补偿控制器对摄动力干扰、内部参量变化等影响进行抑制。如图6所示,系统在第1次参数迭代后由于执行器失效故障,角速度误差和四元数误差在故障发生初期都有较为明显的震荡,并且相对于无故障情形收敛较慢。经过4次参数迭代后,如图7所示,角速度误差震荡逐渐减小而四元数误差震荡和超调现象得到明显减缓,并保证四元数最小误差数量级为10-3。证明了本文所提出的容错控制针对执行器轻微失效故障,以及摄动力干扰、参数变化等影响都具有较好的控制能力,并能保证姿态的高精度鲁棒性。
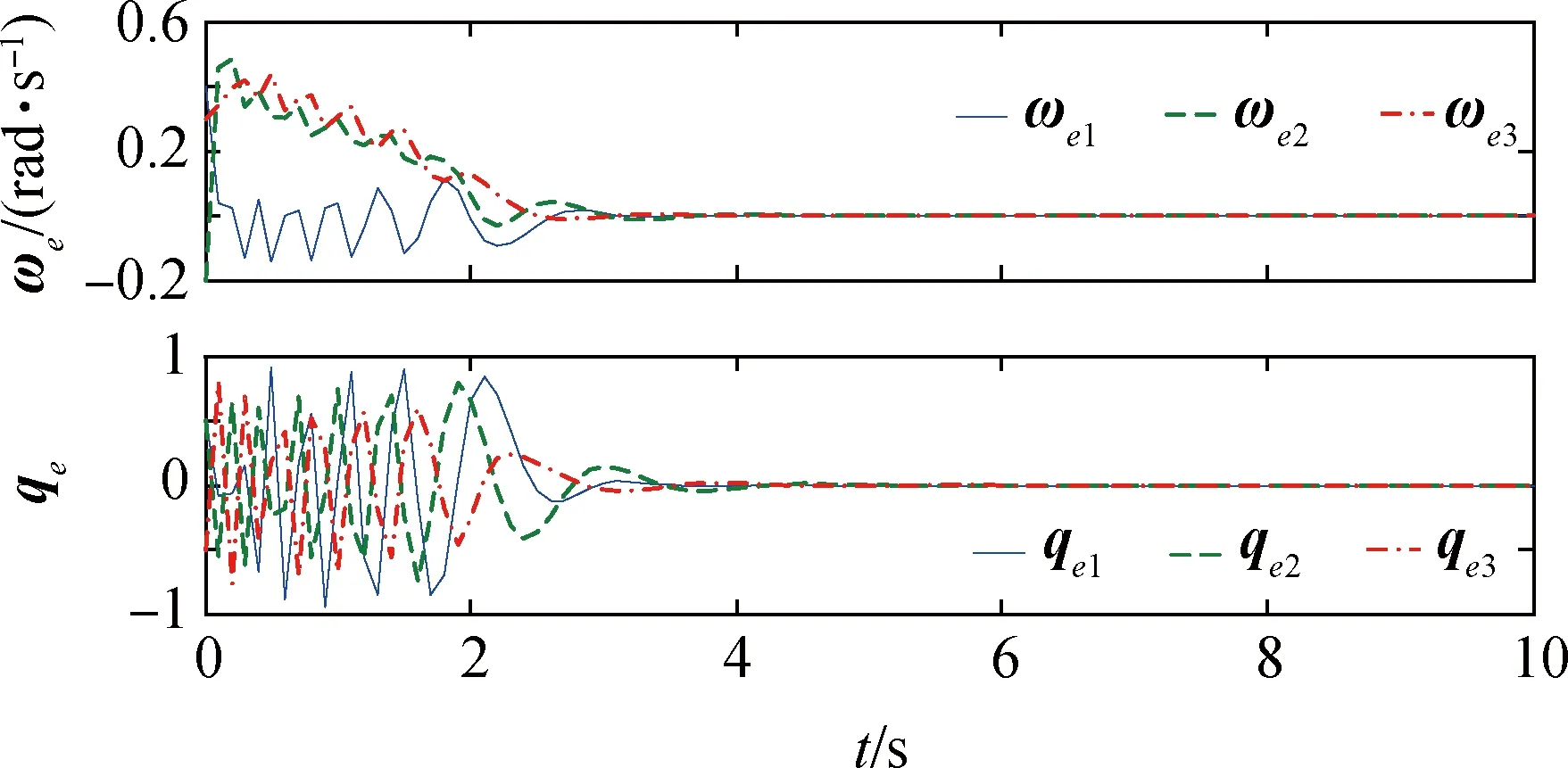
图6 部分失效故障下四元数与角速度误差(1次参数迭代后的结果)Fig.6 Quaternion and angular velocity errors for partial failure motion (first iteration)
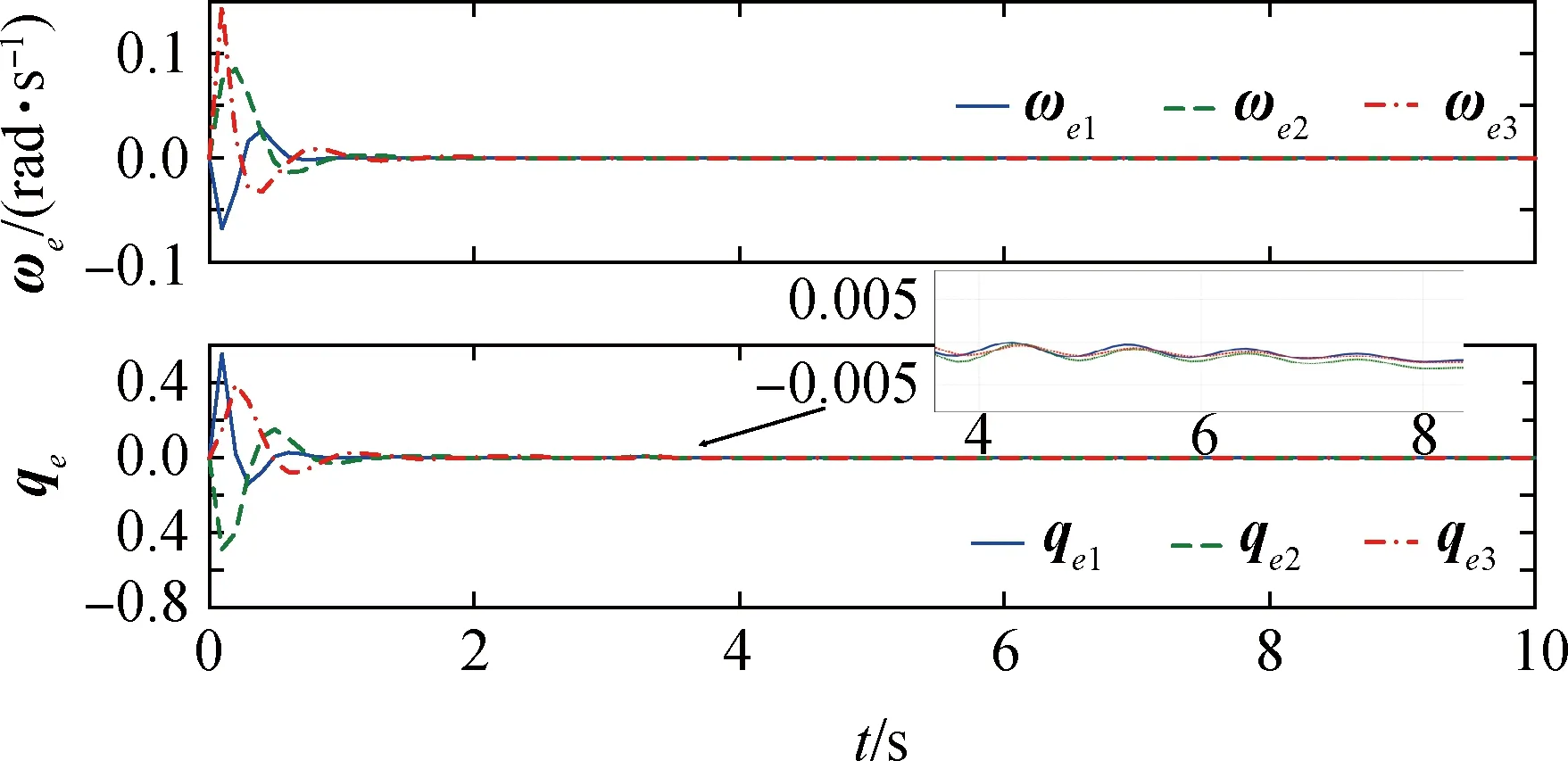
图7 部分失效故障下四元数与角速度误差(4次参数迭代后)Fig.7 Quaternion and angular velocity errors for partial failure motion (forth iteration)
5.4 完全失效故障情形


第5.3节中部分失效故障由于第二组控制器的补偿而对控制性能影响较小,但当同时出现完全失效和部分失效故障时对系统安全性将产生较大影响。由下面图8~11所示,系统在第1次参数迭代后由于执行器失效故障程度较大,角速度误差和四元数误差都出现了缓慢收敛的情况。经过7次参数迭代,所设计的控制器基本消除了执行器完全失效带来的较危险影响,保证了系统的稳定性,并一定程度上维持了无故障情况下的控制性能。从图8~图11显示出,角速度误差随迭代次数的增加逐渐减小震荡幅度,而四元数最小误差在第7次参数迭代后保持在10-2数量级内,并能够随着迭代次数增加逐渐向更高精度收敛。进而证明了当出现执行器完全失效故障,本文设计的控制器也能保证探测器系统的鲁棒性,并能在有限次参数迭代后保证姿态控制的高精度和高稳定性,使得探测任务能够安全完成。
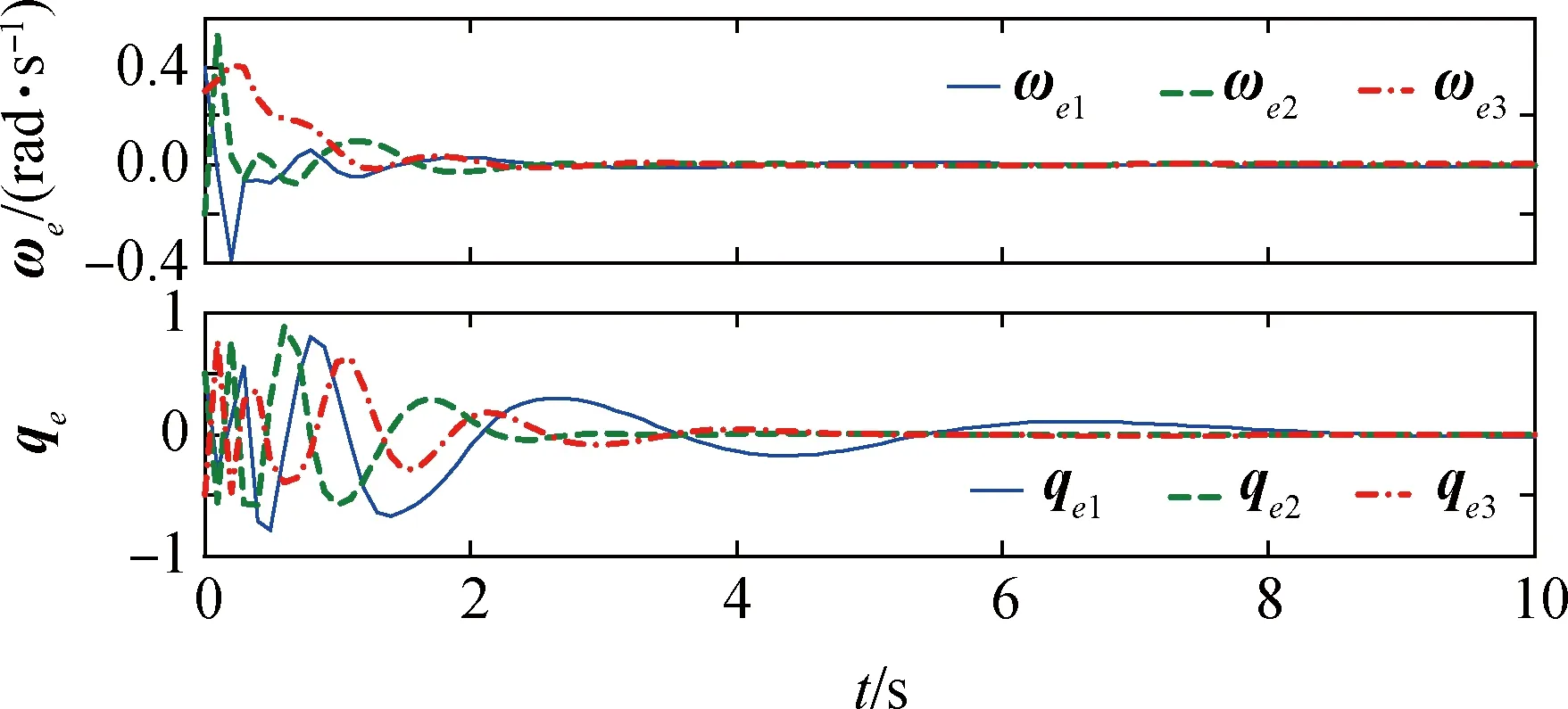
图8 完全失效故障下四元数与角速度误差(1次参数迭代后)Fig.8 Quaternion and angular velocity errors for full failure motion(First iteration)
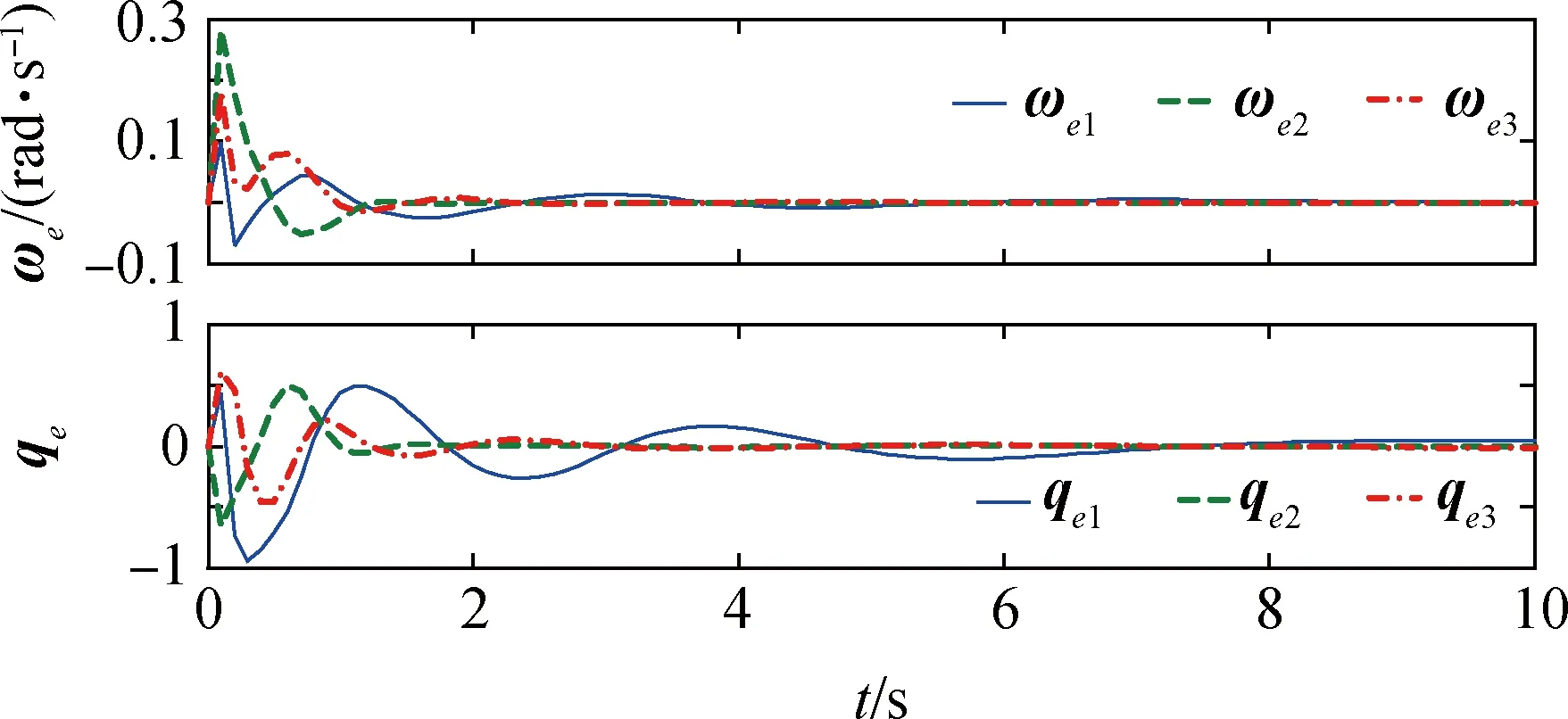
图9 完全失效故障下四元数与角速度误差(3次参数迭代后)Fig.9 Quaternion and angular velocity errors for full failure motion(Third iteration)
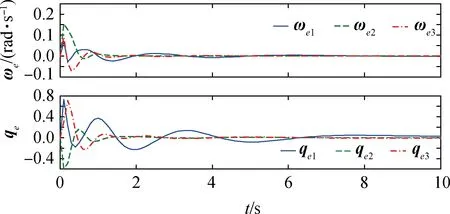
图10 完全失效故障下四元数与角速度误差 (5次参数迭代后)Fig.10 Quaternion and angular velocity errors for full failure motion(Fifth iteration)
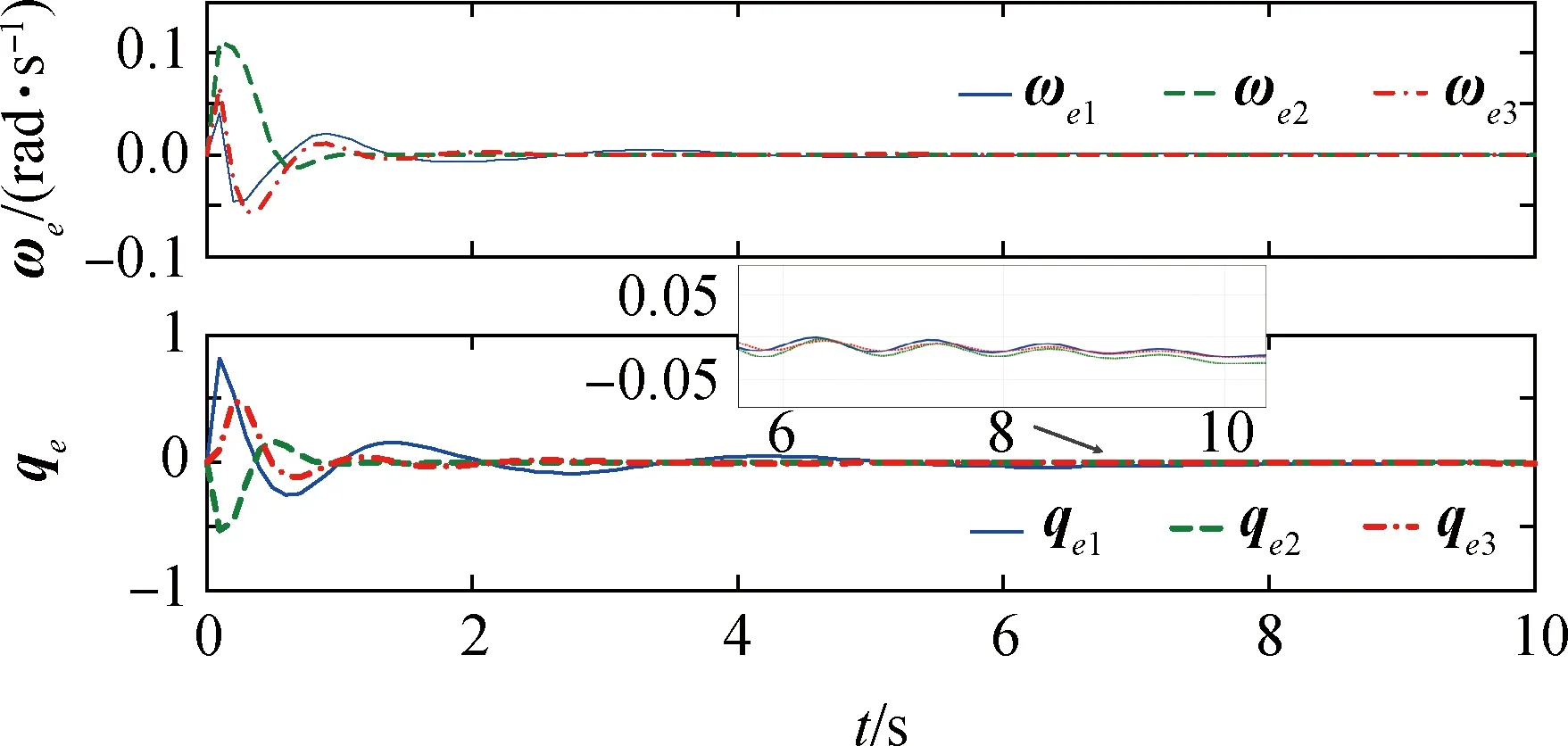
图11 完全失效故障下四元数与角速度误差(7次参数迭代后)Fig.11 Quaternion and angular velocity errors for full failure motion(Seventh iteration)
6 结束语
本文针对小行星绕飞探测任务姿态容错控制问题,综合考虑外部干扰力矩和内部参数不确定性以及执行器故障情况,设计了一种自适应迭代学习容错控制器。该控制方法将自适应算法在线参数调整的特点以及迭代学习算法对重复性干扰有效抑制的特点进行了融合,同时引入自适应神经网络对系统不确定部分进行估计。最后基于Lyapunov方法从理论上证明了系统的收敛性、对飞轮故障的容错能力,并通过计算机仿真分析对算法的可行性和有效性进行了验证。本文在容错控制算法设计过程中没有考虑实际情况中执行器输出受限问题,这一问题留待我们后续的跟进研究。
References)
[1] 崔平远,乔栋. 小天体附近轨道动力学与控制研究现状与展望J]. 力学进展,2013,43(5): 526-539.
CUI P Y,QIAO D. State-of-the-art and prospects for orbital dynamics and control near small celestial bodies J]. Advances in Mechanics,2013,43(5): 526-539(in Chinese).
[2] HU W,SCHEERES D J. Spacecraft motion about slowly rotating asteroidsJ]. Journal of guidance,control,and dynamics,2002,25(4): 765-775.
[3] SCHEERES D J,HU W. Secular motion in a 2nd degree and order-gravity field with no rotationJ]. Celestial Mechanics and Dynamical Astronomy,2001,79(3): 183-200.
[4] HU W. Orbital motion in uniformly rotating second degree and order gravity fieldsM]. Michigan:UMI,2002.
[5] 武江凯,王开强,张柏楠,等. 载人小行星探测轨道设计J]. 中国空间科学技术, 2013, 33(1):1-6.
WU J K, WANG K Q, ZHANG B N,et al. Trajectory design of crewed exploration to asteroidJ]. Chinese Space Science and Technology, 2013, 33(1):1-6(in Chinese).
[6] HIRABAYASHI M,MORIMOTO M Y,YANO H,et al. Linear stability of collinear equilibrium points around an asteroid as a two-connected-mass: application to fast rotating Asteroid 2000EB 14J]. Icarus,2010,206(2): 780-782.
[7] SCHEERES D J. Orbit mechanics about asteroids and cometsJ]. Journal of Guidance,Control,and Dynamics,2012,35(3): 987-997
[8] KUMAR K D. Attitude dynamics and control of satellites orbiting rotating asteroidsJ]. Acta Mechanica,2008,198(1-2): 99-118.
[9] REYHANOGLU M,KAMRAN N N,TAKAHIRO K. Orbital and attitude control of a spacecraft around an asteroidC]. 2012 12th International Conference on Control, Automation and Systems (ICCAS),Jeju Island, South Korea. IEEE, 2012: 1627-1632.
[10] WU B,POH E K,WANG D,et al. Satellite formation keeping via real-time optimal control and iterative learning controlC]. 2009 IEEE Aerospace conference, Big Sky, Montana. IEEE, 2009: 1-8.
[11] WU B,WANG D,POH E K. High precision satellite attitude tracking control via iterative learning controlJ]. Journal of Guidance,Control,and Dynamics,2014,38(3): 528-534.
[12] 管宇,张迎春,沈毅,等. 基于迭代学习观测器的卫星姿态控制系统的鲁棒容错控制J]. 宇航学报,2012,33(8): 1080-1086.
GUAN Y,ZHANG Y C,SHEN Y,et al. Robust fault-tolerant control for satellite attitude control system based on iterative learning observerJ]. Journal of Astronautics,2012,33(8):1080-1086(in Chinese).
[13] CHOI J Y,LEE J S. Adaptive iterative learning control of uncertain robotic systemsJ]. IET Control Theory and Applications,2000,147(2): 217-223.
[14] CHIEN C J,YAO C Y. Iterative learning of model reference adaptive controller for uncertain nonlinear systems with only output measurementJ]. Automatica, 2004, 40(5): 855-864.
[15] FANGY,FEEMSTER M G,DAWSOM D M,et al. Nonlinear control techniques for the atomic force microscope systemC]∥ASME 2002 International Mechanical Engineering Congress and Exposition,New Orleans, Louisiana,2002: 373-380.
[16] 刘林,胡松杰,王歆. 航天动力学引论M]. 南京:南京大学出版社,2006: 86-90.
[17] CHIEN C J. A combined adaptive law for fuzzy iterative learning control of nonlinear systems with varying control tasksJ]. IEEE Transactions on Fuzzy Systems,2008,16(1): 40-51.
[18] LI S,PENG Y M. Neural network-based sliding mode variable structure control for Mars entryJ]. Proceedings of the Institution of Mechanical Engineers Part G: Journal of Aerospace Engineering,2011,226(11): 1373-1386.
[19] LIANG C,LI Y. Attitude analysis and robust adaptive backstepping sliding mode control of spacecrafts orbiting irregular asteroidsJ]. Mathematical Problems in Engineering,2014,2014(77):1-15.
[20] 梁春辉. 小天体附近探测器运动的轨道和姿态控制方法研究D]. 长春:吉林大学,2015.
LIANG C H.Research on orbital and attitude control for proximity motion of small body spacecraftD]. Changchun:Jilin University, 2015(in Chinese).
(编辑:车晓玲)
Adaptive iterative learning based fault tolerant control for asteroid orbiting
HUANG Yixin1,2,LI Shuang1,2,*,JIANG Xiuqiang1,2
1.CollegeofAstronautics,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China2.LaboratoryofSpaceNewTechnology,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China
Considering the probe actuator failures,parametric uncertainties and external disturbances,an adaptive iterative learning based fault tolerant control method was designed for asteroid orbiting. The controller was divided into two parts:robust iterative learning component and neural network iterative learning component. For the robust iterative learning component,a sliding-mode-like strategy with adaptive iterative learning law was applied to maintain the stability and improve the attitude tracking accuracy in case of actuator failures. For the neural network iterative learning component,a radial basis function(RBF) neural network based adaptive approximation was introduced to estimate the system uncertainty,with parameters adapted online to maintain dynamic performance. In addition, numerical simulations show that the method achieved the error in the order of 10-2magnitude under the actuator failure conditions, highlights the robust and high precision attitude tracking performance.
asteroid probe; fault tolerant control; adaptive iterative learning; neural network; actuator failures
10.16708/j.cnki.1000-758X.2017.0002
2016-09-13;
2016-12-23;录用日期:2017-01-24;
时间:2017-02-16 16:36:17
http:∥www.cnki.net/kcms/detail/11.1859.V.20170216.1636.001.html
国家自然科学基金(61273051,11672126);上海航天科技创新基金(SAST2015036);中国科学院太空应用重点实验室开放基金(LSU-2016-04-01,LSU-2016-07-01);江苏省普通高校研究生科研创新计划(SJLX15_0136)
黄怡欣(1991-),女,硕士研究生,hyx_992@126.com,研究方向为航天器姿态控制、容错控制
*通讯作者:李爽(1978-),男,博士,教授,博士生导师,lishuang@nuaa.edu.cn,研究方向为航天器动力学与控制,深空探测技术,航天技术新概念
黄怡欣,李爽,江秀强. 基于自适应迭代学习的小行星绕飞容错控制J].中国空间科学技术,2017,37(1):1-10.HUANGYX,LIS,JIANGXQ.AdaptiveiterativelearningbasedfaulttolerantcontrolforasteroidorbitingJ].ChineseSpaceScienceandTechnology, 2017,37(1):1-10(inChinese).
V
A
http:∥zgkj.cast.cn
