妙解函数图象问题

桂燕

图象作为表示函数的重要形式之一，具有直观、明了的特点.考生在高中数学的学习过程中，要能够结合已知条件来识别图象，学生要能够根据相关图形匹配出其相对应的函数解析式，当题干中没有图象时，考生要能够应用数形结合来解答相关问题.本文以近三年来高考中出现的图像题为载体，分析图象题的考察方式及解题方法，以达到抛砖引玉之效.

一、考察内容

纵观近三年各个省市的高考题，基本上每年的每一套数学试卷中都会有关于函数图象的题目，从选择题、填空题到大题均有涉及.分析近三年以来的试题，不难发现函数图象题的考察主要包括函数解析式、函数的定义域、值域及函数的单调性、奇偶性、周期性等函数的基本特性，再根据这些性质对函数图象进行具体分析判断.

二、真题精讲

例1 （2016四川文科，4）

为了得到函数y=sin（x+π3）的图象，只需把函数y=sinx的图象上所有的点（ ）.

A.向左平行移动π3个单位长度

B.向右平行移动π3个单位长度

C.向上平行移动π3个单位长度

D.向下平行移动π3个单位长度

答案：A

解析

由题意，为得到函数y=sin（x+π3），只需把函数y=sinx的图象上所有点向左移π3个单位，故选A.

点评 这道题目考察的是三角函数图象的平移问题，而三角函数作为特殊的函数，其图象具有周期性的特点，考生经常要充分结合函数的周期性进行求解.

例2 （2016山东文科，17）

设f（x）=23sin（π-x）sinx-（sinx-cosx）2.

（Ⅰ）求f（x）的单调递增区间；

（Ⅱ）把y=f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移

π3个单位，得到函数

y=g（x）的图象，求g（π6）的值.

答案：（Ⅰ）f（x）的单调递增区间是

把y=f（x）圖象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到

y=2sin（x-π3）+3-1的图象，再把得到的图象向左平移π/3个单位，得到

y=2sinx+3-1的图象，即g（x）=2sinx+3-1.

所以g（π6）=2sinπ6+3-1=3.

点评 这道题考察了三角函数的图象和性质，主要考察了三角函数图象的伸缩变换.需要注意，图象纵向伸缩，只需要在函数值前边乘以变化的倍数即可；图象横向伸缩，需要变换函数解析式中的周期.

例3 （2016全国卷理科，12）

已知函数f（x）（x∈R）满足

f（-x）=2-f（x），若y=x+1x与y=f（x）图象的交点为（x1，y1），（x2，y2），…，（xm，ym），则

mi=1（xi+yi）=（ ）.

A.0 B.m C.2m D.4m

答案：B

解析 由f-x=2-fx得fx的图象关于0，1对称，而y=x+1x=1+1x的图象也关于0，1对称，

∴对于每一组对称点xi+xi′=0，yi+yi′=2，

∴∑mi=1xi+yi=∑mi=1xi+∑mi=1yi=0+2·m2=m，故选B.

点评 这道题考察的是函数图象的对称性，函数图象的对称问题在高中最常见的有三种：关于x轴对称，关于y轴对称，关于原点对称，考生要熟练掌握并运用这三种对称，其他的对称基本上都是在这三种情况的基础上演变而来.

例4 （2015全国安徽文科，10）函数f（x）=ax3+bx2+cx+d的图象如图1所示，则下列结论成立的是（ ）.图1

解析 由函数f（x）的图象可知a>0，令x=0d>0，又f ′（x）=3ax2+2bx+c，可知x1，x2是f ′（x）=0的两根，由图可知x1>0，x2>0，∴x1+x2=-2b3a>0x1x2=c3a>0b<0c>0；故A正确.

点评 这道题考察了考生通过函数的图象来判断函数解析式中系数的符号，需要结合函数图象的单调性、极值等特点来判断.

例5 （2014全国卷Ⅰ理科，6）

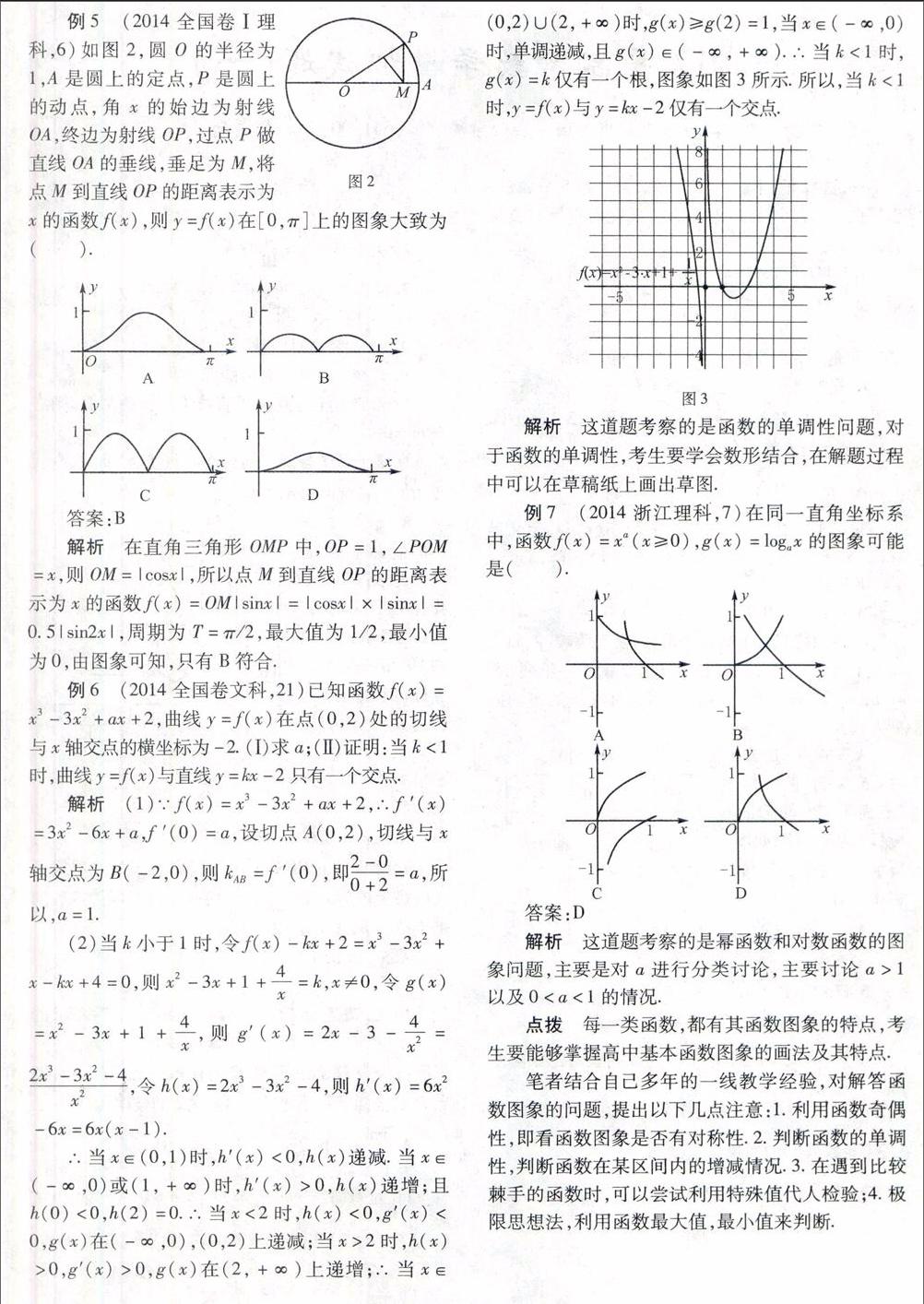
如图2，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，过点P做直线OA的垂线，垂足为M，将点M到直线OP的距离表示为x的函数f（x），则y=f（x）在＼[0，π＼]上的图象大致为（ ）.

答案：B

解析 在直角三角形OMP中，OP=1，∠POM=x，则OM=|cosx|，所以点M到直线OP的距离表示为x的函数f（x）=OM|sinx|=|cosx|×|sinx|=0.5|sin2x|，周期为T=π/2，最大值为1/2，最小值为0，由图象可知，只有B符合.

例6 （2014全国卷文科，21）

已知函数f（x）=x3-3x2+ax+2，曲线y=f（x）在点（0，2）处的切线与x轴交点的横坐标为-2.（Ⅰ）求a；

（Ⅱ）证明：当k<1时，曲线y=f（x）与直线y=kx-2只有一个交点.

图3

解析 这道题考察的是函数的单调性问题，对于函数的单调性，考生要学会数形结合，在解题过程中可以在草稿纸上画出草图.

例7 （2014浙江理科，7）

在同一直角坐标系中，函数f（x）=xa（x≥0），g（x）=logax的图象可能是（ ）.

答案：D

解析 这道题考察的是幂函数和对数函数的图象问题，主要是对a进行分类讨论，主要讨论a>1以及0

点拨 每一类函数，都有其函数图象的特点，考生要能够掌握高中基本函数图象的画法及其特点.

笔者结合自己多年的一线教学经验，对解答函数图象的问题，提出以下几点注意：

1.利用函数奇偶性，即看函数图象是否有对称性.

2.判断函数的单调性，判断函数在某区间内的增减情况.

3.在遇到比较棘手的函数时，可以尝试利用特殊值代人检验；

4.极限思想法，利用函数最大值，最小值来判断.