基于Floyd算法的旅游线路优化

杨 柳，李苗苗，程 越

(上海工程技术大学 管理学院，上海 201620)

基于Floyd算法的旅游线路优化

杨 柳，李苗苗，程 越

(上海工程技术大学 管理学院，上海 201620)

为游客设计合理的游览线路，尽量达到费用最少、旅游体验最好的效果。以分布决策、逐步优化为指导，利用Matlab软件进行Floyd运算寻找最短路径，以出发地为中心在全国范围内，划分分支线；以省会为中心，在省内构建游览路线的哈密顿圈(Hamilton)，再根据时间、成本，进行对各省份之间进行优化合并。假设游客的常住地为西安，设计出了两条线路：一是自驾方式出行的最短路径，二是可换乘飞机、高铁，成本最低的旅游线路。文中将所建立的模型进行了推广应用，变化了出发地点和景区，并针对游客和相关部门给出了相应的建议。

Floyd算法；Matlab；最短路径；哈密顿圈

随着生活水平的提高国内旅游人数急剧增多，中国成为世界第一国内旅游市场。人们对旅游的要求也越来越高，但由于旅游景点众多、时间资金问题制约，不论是游客还是景区市场推广者都需要规划旅游线路，提高旅游体验的满意度，即线路最优和费用最优[1-5]。旅游既是一种时间的安排，又是一种成本的支出，合理的线路安排可以使游人能够在最短的时间获得最大的观赏效果，将每个景点合理贯穿起来[6-9]。运用Floyd算法为游客安排旅游线路，从而实现线路最优、费用最优。

1 模型建立和假设

2015年10月8日国家旅游局新增14个景点，全国共201个5A级景区名单，假设一位自驾游爱好者拟按此景区名单制定旅游计划，实现若干年游览全国5A级景区的目的[10]。该游客常住地是西安，想要在若干年游遍全国201个5A级景区。一是全程自驾，为其规划设计旅游线路；二是考虑费用问题，假如3人同行，综合考虑前述全程自驾、先乘坐高铁或飞机到达省会城市后再租车自驾到景区等出行方式，设计一个10年游遍所有201个5A景区、费用最优、旅游体验最好的旅游线路，旅游要求具体如表1所示。

表1 旅游安排具体要求

本研究的前提假设：(1)假定游客尽可能多的玩够15天，避免路途重复，节约游玩时间和成本；(2)行车平均时速恒定，且不受天气、路况等客观因素的影响；(3)不考虑交通意外等突发事故，并且旅行者在行车过程中，除在省会和景点停留外，不做任何停留。

2 最短路径问题分析与解答

旅游线路的最优规划实质就是求图上最短路径问题。由题中所给的各省会之间的直达路径，利用Floyd 算法求出任意两点间的最短路径，任意两个顶点用一条边相连，边的权值为这两点的最短距离，这样就可以构造出一个完全图。西安X1到其他省会的30个Z1，Z2，Z3，…，Z30之间旅游景点的安排，通过合理的规划，减少出行时间，从而使旅行者在规定的出行时间内游玩更多的地方[11-13]。

首先采用方法T对西安X1到其他省会的30个Z1，Z2，Z3，…，Z30进行分组，假设将其分为n组(n=1,2,…,30)，分别记为V1，V2，…，VK。设VK={Zl1，Zl2，…，Zlk}分组需要满足以下约束条件：每一个分组都需要包含西安X1，每个分组要包括西安和所有的省会。

设旅行者每次出行到达Zj1，Zj2，…，Zjk的旅游景点，完成这些景点游玩，形成一条路径，即对应一个闭合图形。旅行者行车从西安出发依次旅游景点Zj1，Zj2，…，Zjk游玩后再返回西安的旅游线路记为Zj1，Zj2，…，Zjk，对应完全图中的圈X1，Zj1，Zj2，…，Zjm，X1。两个旅游景点之间的最短距离记为|Z1Zm|。由于在完全图中，任意两点都相邻，当旅行者从西安出发到省会及旅游景点，再回来，则视为一条路径。这样，每一条路与完全图中的哈密顿圈一一对应，只需要研究完全图中经过景点的圈即可。

2.1 省份之间模型建立

行程和游玩时间对旅游线路规划起到约束，首先必须考虑如何进行区域划分，再进行区域内优化。在整个线路优化过程中，采用分段决策的思想，首先将全国201个景点按省份进行分组，寻找省份内最短路径，省份内景点调整优化。其次毗邻省份之间优化调整，逐步将全国景点进行优化调整的思路，反复利用Floyd算法合并优化[14]。最终形成全国出行最优线路图。

基于Floyd算法，将各省会之间距离输入Matlab，得出了省份之间最短距离，经过GIS数据库验证，证实了该结论。考虑到地理面积覆盖，距离在-20～20 km范围区间，在高速路上行驶时间在15 min以内，视其为合理范围，那么就可以得到10条主干线，如图1所示。

以西安为中心到全国各地有10条分支线，本文以直线代曲线表示方向，简化作图。在优化调整过程中，以全国10个分支线为基准，对分支线所经省市进一步优化。

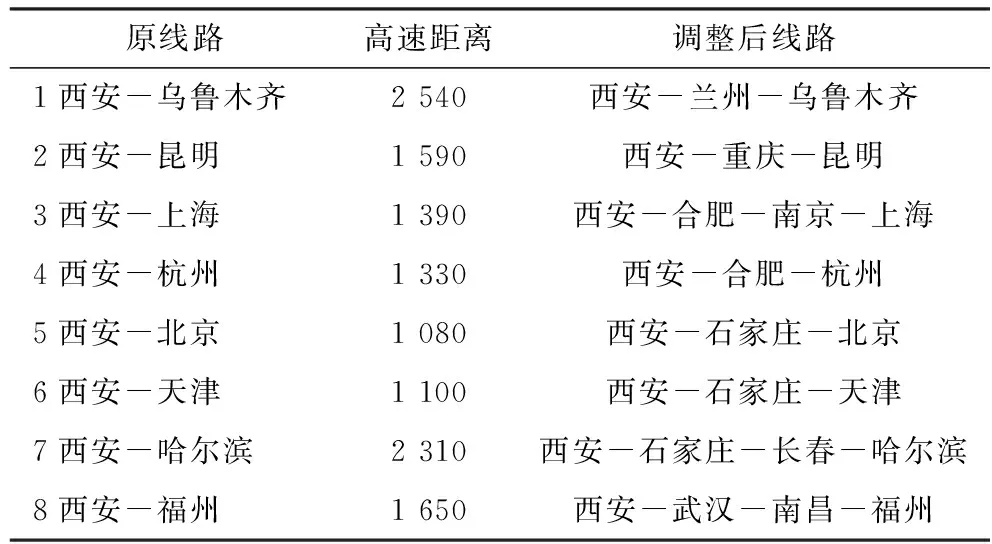
表2 以西安为中心旅游线路规划 /km

2.2 省内景点模型建立

利用GIS数据库，获取省内各景点之间的距离，统计出景点之间的需要的行程时间。再次利用Floyd算法，生成了景点之间的最短距离。反复使用Floyd运算求矩阵，以山西7个景点为例的编程代码，如图2所示，其中7×7矩阵中的数值为任意两景点间的距离，进行运算可得D矩阵和R矩阵，在所得矩阵基础上选用最小元素法构成一个哈密顿圈(Hamilton)，即形成省会到省内各景点的游玩线路闭合圈。按照此方法，各省内都可求出游览的最短路径的哈密顿圈。

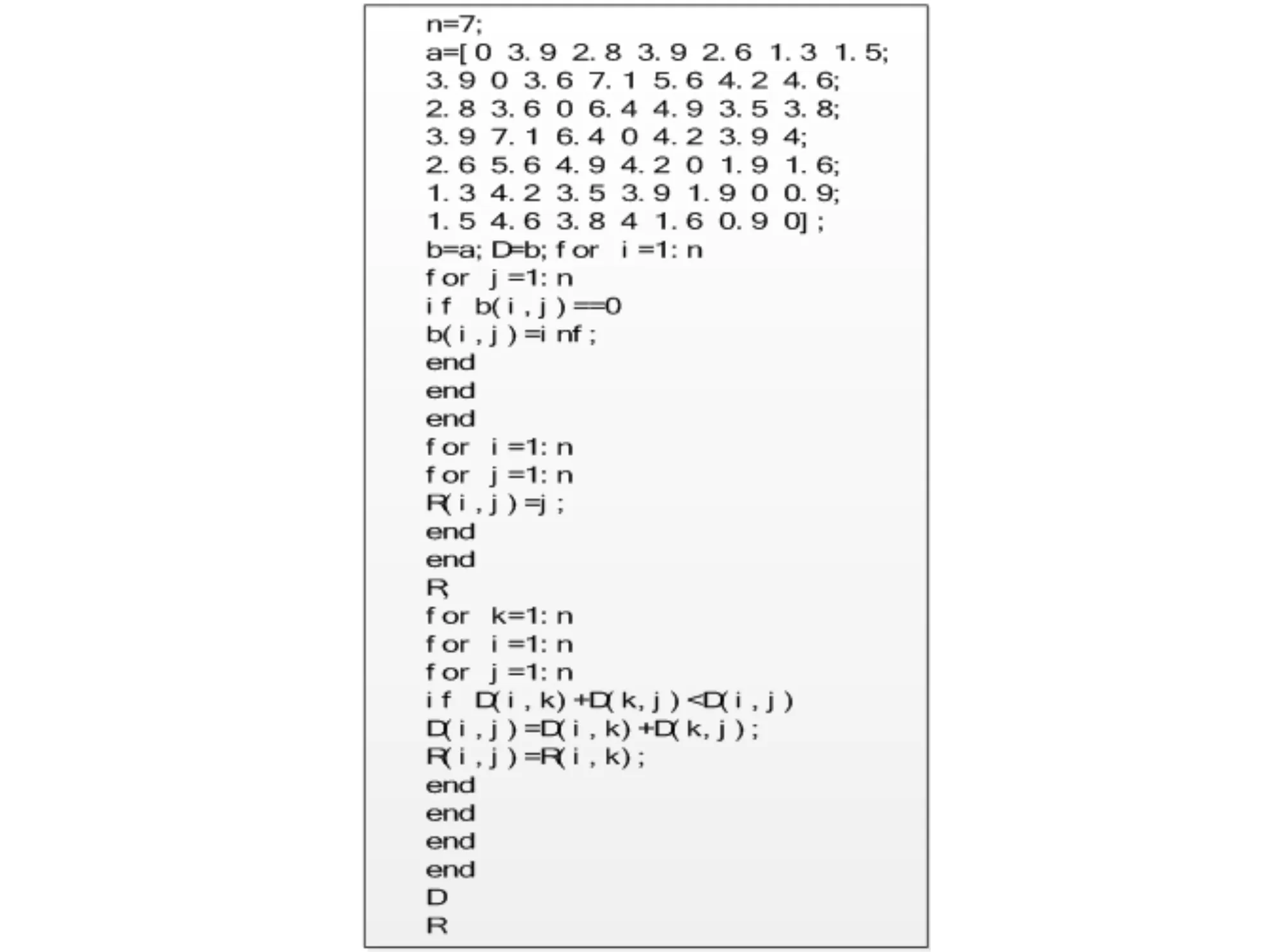
图2 Matlab进行Floyd算法程序代码

以山西为例，利用Floyd算法和Matlab软件进行计算结果，可得出游览路径⑦-⑥-①-⑤-④-③-②-⑦这样一个哈密顿圈，即可选择的旅游线路为：晋中市平遥县平遥古城景区→晋中市乔家大院文化园区→太原市→晋中市介休市绵山风景名胜区→晋城阳城县皇城相府生态文化旅游区→忻州五台山风景名胜区→大同云冈石窟，形成一个闭合的回路。通过上述方式，全国各省内景点依次构成封闭的哈密顿圈。

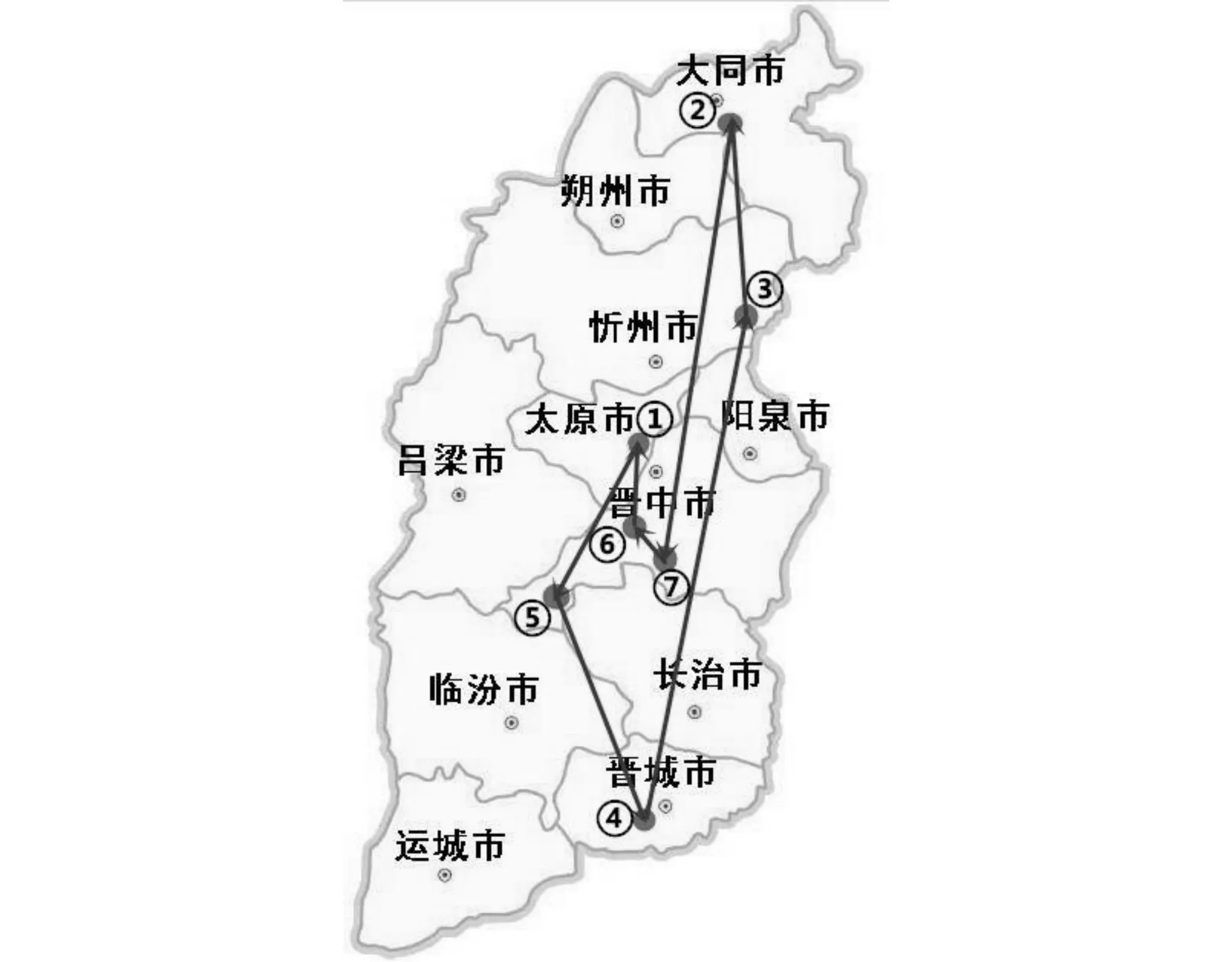
图3 山西游玩路线哈密顿圈

2.3 出行线路进一步优化

基于安全考虑，行车时间限定于每天7:00～19:00之间，且每天开车时间不超过8 h；在每天的行程安排上，若安排全天游览则开车时间控制在3 h内，安排半天景点游览，开车时间控制在5 h内；在高速公路上的行车平均速度为90 km/h，在普通公路上的行车平均速度为40 km/h。景区开放时间统一为8:00～18:00。根据两地的实际距离和速度，就可得行车时间。

基于上述因素，需要对已有线路进行下一步优化。以浙江省为例，研究发现旅行者以此线路游玩浙江省全部5A级景区仅需10天，但考虑到有些地方景点较少，利用省份的划分，在支干线上进行合并优化。那么，根据每次出行时间不超过15天的因素，可以考虑将其他线路与之合并，到达出行时间尽可能接近15天，避免了来回路程的重复，同时依据地域的临近原则，节约出行成本，进行的合并线路形成更为优化的旅行路线，即“西安-浙江-上海-西安”出行线路。

对全国10大支线上省份之间进行合并优化，在出行不超过15天因素的限制下，最终形成24条旅游线路。经核算，该旅行者至少需要12年，才能游遍全国5A级景区。

3 费用最优问题的分析和解答

在费用问题上需要考虑交通方式的改变，提供了时间的充裕，在使用时间相对较少的情况下，使得费用最少、旅游体验最好的旅游线路。

在最短路径问题的基础上根据Floyd算法，可以得到省内的游览路线。省内的游览路线已经优化调整，考虑到省内景点与省内景点距离较近，可乘坐高铁或飞机到达景区相邻的省会城市，而后采用租车的方式自驾到景区游览。步骤如下：

步骤1 在上述结论的基础上，考虑到出行方式多样化和满意原则，并采用分部决策的方式，24条线路进行优化，即选择综合性价比高的线路，并得出游玩线路表；

步骤2 在最新线路表的基础上，对线路景点的行车费用、住宿、景区费用、高铁、飞机费用、租车等费用进行核算，依次得出各线路所需费用；

步骤3 综合分析，得出旅行者每次出行具体线路和旅行费用；

步骤4 对模型进一步优化。

3.1 旅行线路优化问题

依据最短路径问题得出的旅行线路表，旅行者可以综合考虑高铁、飞机、自驾等出行方式，在其他条件不变的基础上，可以对旅行线路进一步优化，从而得到费用最优和旅行体验最好的旅行线路。

由最短路径问题结论可知，省内游玩线路为最优线路。现引入出行方式和旅行体验因素，为更加准确的分析和评估旅行线路，对旅游体验最好的旅游线路做出以下假设：

假设1 旅行者连续开车超过8 h，即放弃；

假设2 乘坐高铁超过6 h，旅行者放弃，转而选择飞机；

假设3 为提高旅行舒适度，尽量减少换乘次数。

旅行方式的选择受到行程时间、距离、换乘次数等因素的影响，在已有旅游线路的基础上，运用分步决策的方式，综合考虑上述因素对线路进行进一步优化，得出新的优化线路。通过对已有的24条出行线路进行优化，得出以下结论：出行线路由24条线路优化到19条，即12年缩减到9.5年。从而可以看出，灵活选择出行方式，不仅可以缩短旅游所需时间，还可以提高旅游品质，达到费用最优、旅游体验最好的线路。

3.2 旅行线路费用问题

省内的行车时间和游览时间已知，该旅游爱好者3人同行，住宿费简化为省会城市和旅游景区200元/人·天，地级市150元/人·天，县城100元/人·天；高速公路的油耗加过路费平均为1.00元/公里， 普通公路上油耗平均为0.60元/km。由于高速公路和普通公路收费和油费标准不同，查阅相关资料和进行数据分析，发现几省的景点具体行车里程中高速公路与普通公路之比近似为8:2，同时符合二八原则，将这一准则推行至全国其它省份。在优化的旅行线路图中，分别对各优化线路的游玩行车费用、住宿、景区费用及租车费用进行计算和汇总。

3.3 出行线路进一步优化

在线路优化的过程中，发现新疆省内最优游玩线路所需时间已经超过每次出行的预定时间15天，因此，以新疆省为例，依据Floyd原则对新疆周围省市进一步优化。

通过对优化后的游玩线路进行车费的核算，得到新疆和宁夏所需总费用16 268.08元，出行需22天，与上文中新疆和宁夏总费用19 684.78元，出行需19天，相比较节省了3 416.7元，出行增加3天。但是，飞机、高铁与自驾游的灵活出行方式大幅增加了旅行者的旅游舒适度。优化后，得出以下结论：旅行者需出行19次即9.5年，游玩时间需要253天，出行总费用为463 769.74元。

4 模型推广与建议

4.1 模型的推广

常住地的改变或者旅游景点增多，建模思路、方式具有一致性，建模步骤如下：

步骤1 基于Floyd算法，将省会城市间道路信息在Matlab中运算，以省份为单位进行区域划分，形成以游客所在省会为中心的全国分支线；

步骤2 反复运用Floyd算法，得出各省省内景点之间最短距离，各省省内景点分别构建哈密顿圈，即各省省内游玩的行程路线；

步骤3 省份之间线路逐步优化调整；

步骤4 结合行车时间要求和景点开放时间的制约，给出相应的优化行程线路。

对于货物配送、销售人员销售、交通线路规划等问题，本文模型具有一定适用性，可以推广。

4.2 模型的优缺点评价

模型的优点：(1)在模型建立过程中，对全国5A级景点首先采用各省会间最短路径，得出出行主线，其次分别规划各省内景点优化路径，最后得出全国出行优化线路图。这对旅行者旅游具有一定的指导意义；(2)查阅相关文献并且收集大量数据，基于Floyd算法，利用Matlab软件得出所需数据和结论，使用方法的科学性和数据的客观性。模型也存在这一些缺点：(1)分组是在一定的规则下进行的，其结果与其所侧重的原则有较大的关系，不同原则会导致分组情况变化，进而导致线路的变化；(2)充分考虑到全国景点过多，数据过大，出行线路仍有优化空间。

4.3 建议

对于游客来说，旅游的目的是愉悦身心、放松享受生活。以此为出发点，对旅行者给出以下建议：(1)灵活选择出行方式，尽量减少换乘次数和行车时间；(2)各省省内游玩可参考优化线路表，合理选择游玩线路；(3)游玩途中，合理安排住宿、景点选择，得到最优旅游体验。

对于相关部门来说，景区线路优化和市场推广是其工作的重点。以此为目标，对相关部门给出以下建议：(1)强化区域和和各旅游线路的区域合作，加强政府间合作，构建无障碍旅游机制，实现区域旅游合作的规范化和制度化，以达到旅游资源的最优配置；(2)节假日、旅游旺季，可以适度增加车辆，满足客流需求；(3)加大旅游线路的宣传营销力度，塑造整体旅游形象和各旅游线路的特色形象，加强整体营销力度，挖掘潜在的客源市场。

[1] 王徐民,方玉平,张慧慧.旅游线路优化设计[J].中国西部科技,2011(24):35-36.

[2] 耿建忠,吴殿廷,叶倩,等.基于图论的西藏旅游线路评价与优化研究[J].地域研究与开发,2011(1):104-109.

[3] 曹旭,张喆,马少仙.最短路问题在旅游线路优化中的应用[J].科技广场,2012(2):115-118.

[4] 樊守伟,严艳,张少杰,等. Dijkstra算法与旅游路径优化[J].西安邮电大学学报,2014(1):121-124.

[5] 徐秀花,程晓锦,寇怡.蚁群算法在旅游交通线路中的应用[J].北京印刷学院学报,2013(2):48-51,54.

[6] 何红,孙根年.基于教与学优化算法的智能旅游线路优化[J].陕西理工学院学报:自然科学版,2015(1):72-78.

[7] 潘玉侠,梁勤欧.基于遗传算法的旅游线路优化[J].浙江师范大学学报:自然科学版,2011(3):350-354.

[8] 刘斯禹,韩雪,郭天超.基于Matlab图形界面研究李萨如图形及其讨论[J].科技资讯,2016(6):126-127.

[9] 刘冰,曾国军,彭青. 社会网络视角下旅游线路研究-以新疆为例[J].旅游学刊,2013(11):101-109.

[10] 刘宏盈,韦丽柳,张娟.基于旅游线路的区域旅游流网络结构特征研究[J].人文地理,2012(4):131-136.

[11] 胡晓涛,吴成罡.基于虚拟旅游导航智能选择系统的Floyd算法[J].统计与决策,2012(18):74-77.

[12] 王荣,江东,韩惠.基于Floyd方法的最短路径算法优化算法[J].甘肃科学学报,2012(4):110-114.

[13] 王佳,赵宏丽.基于Dijkstra算法的京津冀旅游交通线路优化研究[J].统计与决策,2011(13):81-83.

[14] 侯晓利,薛伟坡,张军委.公交线路选择问题的数学模型与算法[J].统计与决策,2008(18):76-78.

Research of Optimizing Tourism Route Based on the Floyd Algorithm

YANG Liu, LI Miaomiao ,CHENG Yue

(School of Management, Shanghai University of Engineering Science,Shanghai 201620,China)

This paper attempts to design the reasonable tourist path to cost at least as far as possible ,for the tourism experience the best effect. Guided by the optimization of the distribution decisions step by step,firstly,we use Matlab software and Floyd algorithm to find the shortest path, across the country, for the center with origin division branch line;Secondly using the provincial capital as the center, we build a tourist route in the province of Hamiltonian cycle; then according to the time,we optimize the between the provinces merged. The paper assumes that the tourists always live in Xi’an, we design two routes for him: one is the shortest path of drive travel, the other is that the tourist can choose the plane or high iron,the lowest cost of tourism path.We popularize and apply the proposed model in this article-change the place of departure and the change of the scenic spot, and give the corresponding suggestions for tourists and related department.

Floyd algorithm；Matlab；the shortest path；hamiltonian cycle

2016- 07- 05

杨 柳(1991-)，男，硕士研究生。研究方向：旅游管理，企业管理。李苗苗(1991-)，女，硕士研究生。研究方向：旅游管理，领导力。程越(1993-)，男，硕士研究生。研究方向：企业管理。

10.16180/j.cnki.issn1007-7820.2017.01.021

TP301.6

A

1007-7820(2017)01-076-04