基于RAGA的投影寻踪分类模型改进与实例分析

朱成功

(上海理工大学 光电信息与计算机工程学院，上海 200093)

基于RAGA的投影寻踪分类模型改进与实例分析

朱成功

(上海理工大学 光电信息与计算机工程学院，上海 200093)

针对实数编码加速遗传算法(RAGA)在求解投影寻踪分类(PPC)模型陷入局部最优的问题，通过引入区间扩展因子：在变量区间过小时，对变量区间进行适当扩展；在扩展区间"越界"时，即以边界作为变量的取值。并选取合理的局部密度窗口半径R，建立了改进的RAGA-PPC分类模型，并以文献中S县15个乡镇申请粮援项目的投资顺序为例进行验证分析。研究表明，改进的RAGA-PPC模型对样本分类评价，确立指标因素的贡献程度大小具有一定的可行性和广泛的通用性。

实数编码加速遗传算法；区间扩展；窗口半径；投影寻踪分类

自从金菊良等[1]提出加速遗传算法，已在干旱环境监测、自然灾害、水文地质工程地质等众多领域得到了广泛应用[2-4]。相比于标准遗传算法(SGA)，加速遗传算法克服了在实际应用中存在早熟收敛、计算量大和解的精度差等缺点[5]，但目前一些论文并没有对变量区间进行改进，如文献[6]采用了自适应的交叉和变异操作，解决了因交叉概率和变异概率不变而导致过快出现局部收敛的现象，文献[7]提出了基于个体修正模型的改进加速遗传算法，根据各子目标函数值对应因素的重要性程度，运用层次分析法确定各因素的权重，依次采用相应的权重构造总目标函数。

投影寻踪模型(Projection Pursuit Clustering，PPC)是由Friedman和Turkey于1974年提出的，是处理和分析高维数据的新兴统计方法，传统的投影寻踪技术存在计算量大等缺点[8]，因此金菊良等提出用RAGA求解投影寻踪模型[9]。

本文根据实数编码的加速遗传算法(RAGA)的思想，通过改进加速时优化变量的区间来扩大变量的搜索范围：在区间过小时，对加速区间进行适当扩展；当扩展后的区间超过边界时，即以边界值作为优化变量的值。将改进的实数编码加速遗传算法应用于RAGA-PPC模型中，结合文献[10]中的数据及楼文高在文献[11]中的基本定理和推理，验证了改进的RAGA算法，在投影寻踪分类模型中能够求得全局最优解和最优投影方向。

1 改进区间的实数编码加速遗传算法

实数编码的加速遗传算法(RAGA)主要包括选择，交叉，变异和加速等步骤，通过问题域中个体的适应度大小选择个体，逐代演化得到优秀个体。并利用优秀个体逐步缩小优化变量的初始变化区间，达到加速目的。

为一般起见，不妨设优化问题为如下最小化问题

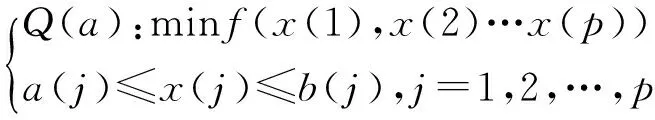
(1)

其中，x(j)为第j个优化变量；[a(j),b(j)]为x(j)的变化区间；p为优化变量的个数；f为目标函数。

(1)初始化。设群体规模为N，生成N组取值为[0,1]上均匀分布的随机数，每组有p个，即{u(i,j)|(i=1-N,j=1～p)}，然后根据线性变换公式x(i,j)=a(j)+u(i,j)×(b(j)-a(j))把u(i,j)变换成[a(j),b(j)]上的优化变量x(i,j)；

(2)选择。将初始化生成的N组优化变量代入目标函数f，得到目标函数值(即适应度值)f(i)(i=1～N)，按目标函数值的大小升序排列，排序后前S个个体为优秀个体，直接进入下一代，剩下(N-S)个个体通过轮盘赌的方式选择，得到第一代N个个体x1；

(3)交叉。第二代子代群体由交叉得到，通过随机挑选父代群体中的两个个体x(x1,j)，x(i2,j)，通过如下线性组合得到两个新的个体x2(k1,j)和x2(k2,j)。

(2)

式(2)中，u为随机数，这样共产生N个子代个体x2；

(4)变异。第三代子代群体由变异得到，通过求目标函数值得到个体x(i,:)(i=1～N)被选择的概率ps(i)，由于目标函数值越小，其选择的概率越小，其变异的概率则越大，因此x(i,:)变异的概率pm(i)=1-ps(i)，从而得到第三代 个个体 。即

(3)

式(3)中，u(j)(j=1～p)，um均为随机数；

(5)迭代。由前面选择，交叉和变异得到的三代群体x1，x2，x3共3N个个体，计算其适应度值，并按照升序排列，取出适应度值靠前的前N个个体作为新的的父代群体，算法转入步骤3；

(6)加速。在进行若干次的选择，交叉，变异操作后，对得到的N个个体x(i,j)=(i=1～N,j=1～p)作如下改进：

1)对于N个个体的任意一列x(:,j)(j=1～p)，其最大值maxx为max(x(:,j))，其最小值minx为min(x(:,j))，则进入下一次迭代的父代xnew由以下公式产生

xnew(i,j)=minx+u×(maxx-minx)

(4)

式(4)中xnew(i,j)(i=1～N,j=1～p)，u为[0，1]的随机数；

2)若在若干次迭代后出现 个个体的某一列陷入局部最优的情况，即某列变量的最大值和最小值几乎相等，即(maxx-minx<ε)，ε为任意一个很小的常数，本文取0.000 1，则需对该列区间进行适当扩展，如下所示

(5)

式(5)中x1为>1的常数，本文取1.1，c2为<1的常数，本文取0.9；

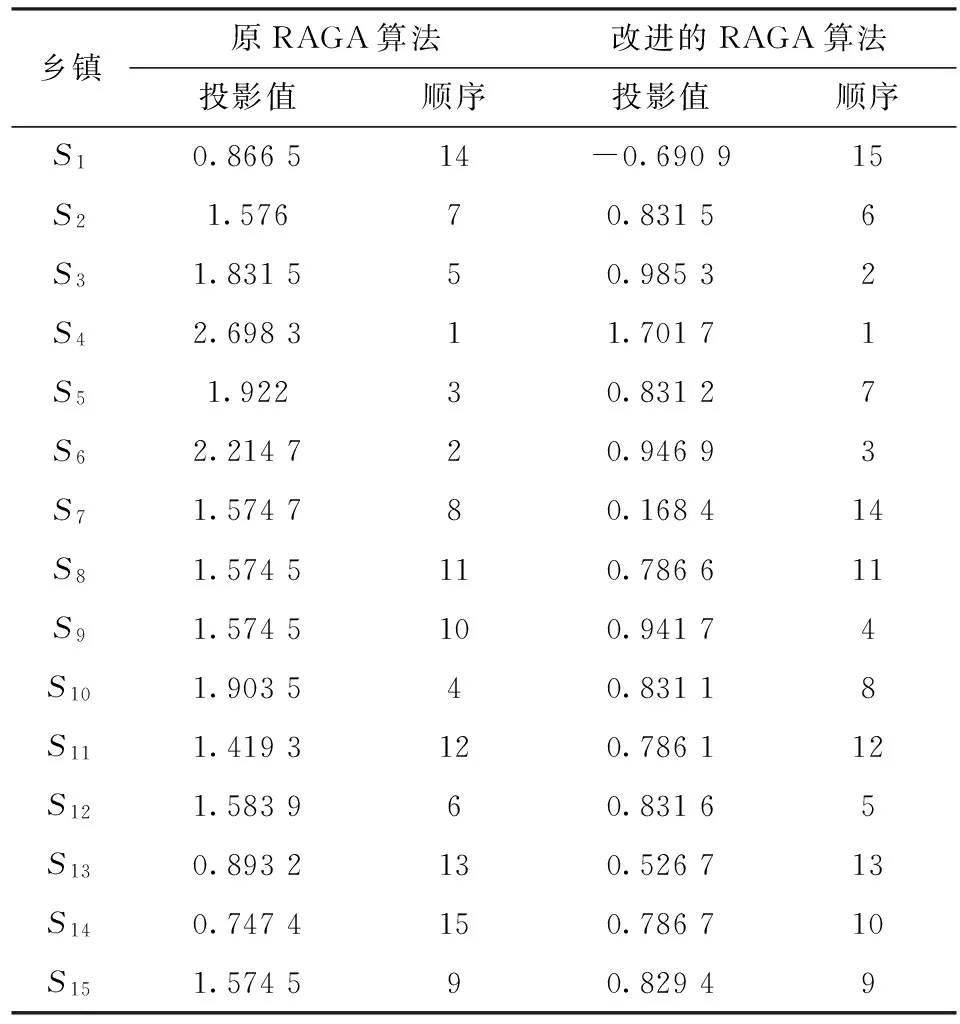
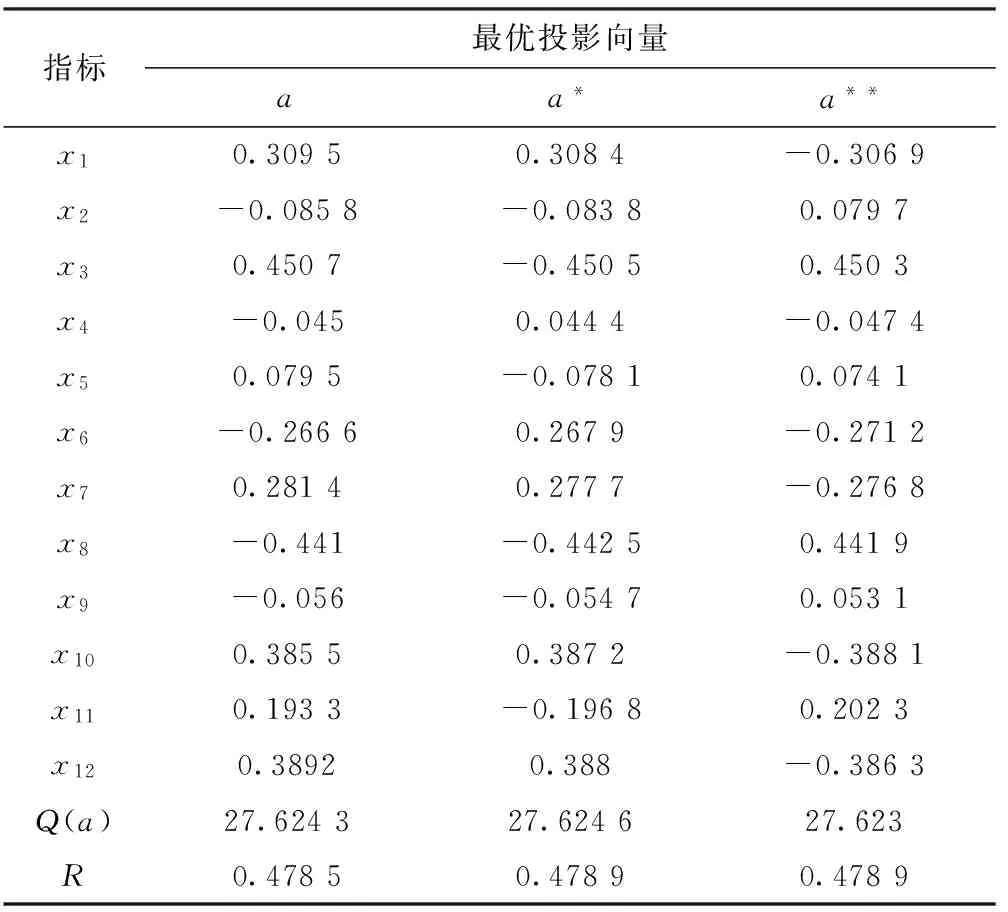
3)若步骤2处理数据后出现maxx>b(j)或minx

maxx=b(j)

(6)

或

minx=a(j)

(7)

此时再将区间扩展后的最大值和最小值代入上式中生成下一次迭代的父代xNEW，然后算法转入步骤3，进行下一轮的演化，如此循环，直至算法达到预定的迭代次数或目标函数值满足条件，算法结束，并将当前群体中的最优个体作为算法的最优化结果。

2 投影寻踪分类模型

投影寻踪模型是一种适用于非线性，处理高维数据的寻优方法，其通过采用某种目标函数使所有样本点形成若干个类，并要求类与类之间尽可能分散，而同一类内的样本点则尽可能密集。具体实现步骤主要包括评价指标归一化处理，构建投影指标函数，优化投影指标函数以及聚类等[9]。设给定数据的第i个样本的第j个指标为x(i,j)(i=1～n,j=1～p)，其中n为样本个数，p为指标个数。

2.1 数据预处理

为了消除数据样本指标量纲不同的影响，需要对数据进行归一化处理。

对于越大越优的指标

(8)

对于越小越优的指标

(9)

其中，xmax(:,j)和xmin(:,j)分别为第j个指标的最大值和最小值；x*(i,j)为样本指标归一化后的值。

2.2 构建投影指标函数

设a(j)为投影方向向量，第i个样本在该投影方向上的投影值z(i)为

(10)

投影指标函数为

Q(a)=Sz·Dz

(11)

(12)

(13)

ri,k=|z(i)-z(k)|

(14)

式中，Sz为样本投影值z(i)的标准差；Dz为局部密度值；E(z)为样本投影值z(i)的平均值；R为局部密度的窗口半径；ri,k为样本i样本k投影值之间的距离。根据楼文高等[11]的研究结果，密度窗口半径R合理取值范围为max(ri,k)/5≤R≤max(ri,k)/3，即将样本分为3～5类，本文取R=max(ri,k)/5。

2.3 优化投影指标函数

当构造的投影指标函数Q(a)达到极大值时即可找到最优投影方向a。即

Q(a)=max(Sz·Dz)

(15)

约束条件为

(16)

2.4 聚类及排序

将由步骤3求得的最优投影方向a代入式(10)各样本点的投影值z(i)。将z(i)与z(k)进行比较,二者越接近，表示样本i样本k倾向于分为同一类。若按z(i)值从大到小排序，则可将样本从优到劣进行排序。若对求得的最优投影方向a的各个分量进行从小到大排序，则可判别各个指标对样本的影响程度，分量值越大，影响程度越大。

3 改进的RAGA-PPC建模实例分析

应用改进后的RAGA-PPC模型，计算文献[10]中S县15个乡镇 申请粮援项目的投资顺序以及判断各个指标因素的贡献程度大小。

根据原文中的要求，选取经济因素、社会因素和自然因素3方面的12个因素作为评价指标，在12项指标因子中：缺水人口比例x1，库区移民率x2，文盲率x7，病床率x8，山坡耕地比例x9，大龄青年比例x10及瓜干比例x12这几项指标因子属于越大越优指标，因此原始数据越大，对该项目的需求度越大；而人均收入x3，人均口粮x4，统销粮x5，人均耕地x6，灌溉面积比例x11这几项指标属于越小越优指标，原始数据越大，对该项目的需求度越小。具体数据见文献[10]。

选定父代初始种群规模N=400，优秀个体数目为50个，迭代20次进行一次加速，利用Matlab编程计算可得到最优投影方向：

a=(0.309 5,-0.085 8,0.450 7,-0.045 0,0.079 5,-0.266 6,0.281 4,-0.441 0,-0.056 0,0.385 5,0.193 3,0.389 2)

各个样本的投影值

z=(-0.690 9,0.931 5,0.985 3,1.701 7,0.831 2,0.946 9,0.168 4,0.786 6,0.941 7,0.931 1,0.786 1,0.831 6,0.526 7,0.786 7,0.829 4)

最优投影指标函数值Q(a)=27.624 3，局部密度窗口半径R=0.478 5。根据求解出的投影值排序，可得如表1所示。

表1 两种算法对比研究

结果分析：

(1)由表1可知，乡镇S4对项目的需求度最大，这与原论文中加速遗传投影寻模型的评价结果一致，从决策上分析，这说明改进的RAGA算法具有一定得适用性；

(2)但对于其他乡镇，改进的方法与原论文有一定的差异。如原文中乡镇S14对该项目的需求度最小，而改进的算法求得乡镇S1的需求度最小；从整体上来看，原文中需求度最小的3个乡镇依次为S14，S1和S13，而改进的算法求得的需求度最小的3个乡镇依次为S1，S7和S13，具有一定的相似性;

(3)为比较两种算法的优劣，计算这两种算法所得的投影指标函数值。根据原文给出的最优投影方向

a=(0.327,0.167 8,0.291 9,0.324 3,0.093 9,0.404 3,0.177 4,0.128,0.183 9,0.298 5,0.349 5,0.457 5)

以及式(10)～式(14)可以求解出Q(a)=0.538 6，小于本文求解的结果(Q(a))=27.624 3，说明原论文中并未求得真正的最优解。

由于本文中R=max(ri,k)/5，即将样本分为五类。根据计算的投影值，值为1.701 7的分为一类，值为0.985 3,0.946 9和0.941 7的分为一类，值为0.831 6,0.831 5,0.831 2,0.831 1,0.829 4,0.786 7，0.786 6,0.786 1的分为一类，值为0.526 7的分为一类，值为0.168 4,-0.690 9的分为一类。即S4为一类，S3，S6，S9为一类，S12，S2，S5，S10，S15，S14，S8，S11为一类，S13为一类，S7，S1为一类，总共5类，且类与类之间投影值差异明显，而类内投影值相对集中，说明将样本分为5类是合理的。

为进一步验证上述结论的可靠性，正确性。根据文献[11]中的定理1同一指标的数据采用式(8)和式(9)进行归一化预处理，其权重必定互为相反数以及相应的结论：通过改变某些指标的归一化方式，从权重是否是互为相反数，便可判定最优化过程是否求得了真正的全局最优解。现做如下试验，采用改进的RAGA算法和式(8)及式(9)求得的最优投影向量为a，改变归一化的方式，令全部指标均为越大越优指标，只用式(8)再次求得的最优投影向量为a*，令全部指标为越小越优指标，只用式(9)求得的最优投影向量为a**。具体数据如表2所示。

表2 3种不同归一化方式下的最优投影向量对比

结果分析：

(1)由表2可知，比较最优投影向量a和a*，a为采用越大越优和越小越优两种归一化方式得到的投影向量，而a*为全部采用越大越优归一化方式得到的投影向量，两者相比，除x3，x4，x5，x6，x11指标的的投影分量互为相反数外，其余皆近似相等。同理，a与a**相比，a**为全部指标采用越小越优归一化方式得到的投影向量，除x3，x4，x5，x6，x11指标的的投影分量近似相等外，其余皆为相反数，这说明改变归一化方式后改进的RAGA算法求得的权重变为了相反数;

(2)再根据3种归一化方式求得的最优投影值可知，3种方式均求得了近似相等的投影值，这符合定理一的结论: 改变指标归一化方式前后，其权重互为相反数，投影函数值保持不变;

(3)综合改进后的RAGA算法求得了更小的最优投影值以及符合了PPC模型的定理及推论，可认为改进的RAGA算法在投影寻踪模型中的应用是有效、正确的;

(4)根据最优投影方向，可进一步判断各指标因素对各个乡镇申请粮援项目的贡献大小。最优投影方向各分量的大小实际上反映了各指标对申请粮援项目的影响程度，值越大则对应的指标对结果的影响程度就越大。最优投影方向向量a表明各个指标对申请粮援项目的影响程度大小依次为人均收入x3，瓜干比例(农作物晒干后与含有水分时的质量比)x12，大龄青年比例x10，缺水人口比例x1，文盲率x7，灌溉面积比例x11，统销粮x5，人均口粮x4，山坡耕地比例x9，库区移民率x2，人均耕地x6，病床率x8。

4 结束语

(1)在RAGA算法加速过程中对不断压缩的优化变量区间进行适当地扩展：在区间小于某个很小的常数ε(本文取0.000 1)时，对区间的上界乘以常数c1(c1>1，本文取1.1)区间的下界乘以常数c2(c2<1,本文取0.9)，可以扩大优化变量的搜索区间，防止变量陷入局部最优。该常数是按照经验选取，其取值并不唯一，当出现越界的情况时即按照式(6)和式(7)处理;

(2)将改进后的RAGA算法应用于PPC模型，选取合理的局部密度的窗口半径R，将样本分为3～5类。研究结果表明，这种改进方案是合理的，并由已知定理证明，改进算法能够求得当前加速次数下的最优解，这能使应用PPC模型的聚类或优序排列的结果更加可靠，也为生产实践中判断各个指标因素的影响程度大小提供了参考。

[1] 金菊良,杨晓华,张国桃,等.非线性环境模型优化的一种数值方法[J].环境工程学报,1997 (S1): 108-112.

[2] 杨晓华,张国桃,金菊良.灰色系统模型GM(1, 1)的参数估计方法[J].干旱环境监测,1998, 12(2):76-80.

[3] 杨晓华,金菊良,张国桃.加速遗传算法及其在暴雨强度公式参数优化中的应用[J].自然灾害学报,1998,7(3):71-76.

[4] 金菊良,丁晶,魏一鸣.加速遗传算法在地下水位动态分析中的应用[J].水文地质工程地质,1999,26(5):4-7.

[5] Mirjalili S. The ant lion optimizer[J].Advances in Engineering Software,2015,83(3):80-98.

[6] 周成成.大型活动突发事件下交通疏散效率评价研究[D].成都:西南交通大学,2014.

[7] 张宇亮,张礼兵,周玉良,等.基于改进加速遗传算法的作物灌水率图修正研究[J].灌溉排水学报,2015,34(11):80-83.

[8] 吴承祯,洪伟,洪滔.基于改进的投影寻踪的森林生态系统生态价位分级模型[J].应用生态学报,2006,17(3):357-361.

[9] 付强,金菊良,梁川.基于实码加速遗传算法的投影寻踪分类模型在水稻灌溉制度优化中的应用[J].水利学报,2002(10):39-45.

[10] 张科举,缑慧娟.加速遗传投影寻踪模型在工程项目决策中的应用研究[J].土木工程与管理学报,2015,32(1):93-96.

[11] 楼文高,乔龙.投影寻踪分类建模理论的新探索与实证研究[J].数理统计与管理,2015, 34(1):47-58.

Based on Projection Pursuit Classification Model Improvement and Analysis of Examples RAGA

ZHU Chenggong

(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology，Shanghai 200093, China)

Aiming at the problem that real-coded accelerating genetic algorithm (RAGA) could not solve global optimal solution of PPC Model, this paper proposes an improvement: when variableinterval is too small, then extends variable interval by an appropriate constant; when the extension crosses the border, set the boundary as the variable’s value. Combining with properRvalue, the improved RAGA-PPC model is established, and using it in food aid project investment order of S county’s 15 towns, more reasonable sequences and each factor’s influence on the investment order are obtained. The results show that the improved RAGA-PPC model has strong applicability and generality of sample classification and evaluation as well as estimating each factor’s contribution.

real-coded accelerating genetic algorithm;interval extension; window radius;projection pursuit clustering

2016- 03- 22

朱成功(1991-)，男，硕士研究生。研究方向：投影寻踪。

10.16180/j.cnki.issn1007-7820.2017.01.030

TP391

A

1007-7820(2017)01-107-05