全极化微波辐射计天线极化纯度的研究
2017-03-29陈文新
邢 妍,陈文新
(中国空间技术研究院 西安分院,陕西 西安 710000)
全极化微波辐射计天线极化纯度的研究
邢 妍,陈文新
(中国空间技术研究院 西安分院,陕西 西安 710000)
天线交叉极化特性使微波辐射计接收的辐射偏离了地球场景辐射原来的极化状态,导致全极化微波辐射计第3和第4个Stokes参数测量值严重偏离真实值。文中建立了天线交叉极化传输模型,引入极化纯度参数,推导出Stokes参数测量值和真实值在非理想极化特性下的关系,消除了天线极化纯度对Stokes参数测量值带来的影响。同时,仿真分析了极化纯度测量不确定度对Stokes参数的影响,在满足测量准确度条件下,对全极化微波辐射计天线极化纯度指标及其测量精度提出了要求,为全极化微波辐射计天线方向图校正奠定了理论基础。
全极化微波辐射计;Stokes参数;极化纯度;不确定度
利用双极化微波辐射计(V和H极化)测量海洋表面风速是早已成熟应用的一门技术,早期研究表明,海洋表面微波散射各向异性特性是由风向引起的[1],星载微波辐射计经过准确定标后,可同时准确地获得海洋表面风速风向信息。后续大量理论研究和实验证实了Stokes参数第3和第4分量的确包含了更多的风向信息。同时,研究表明,T3分量的方位变化受云雨的影响也比其他分量小,T4分量不受Faraday旋转的影响[2]。基于极化辐射测量的优势及其广阔的应用前景,在过去的近20年里人们对全极化微波辐射计测量机理接收机的设计进行了深入研究。由于全极化微波辐射计Stokes参数第3和4分量比垂直、水平极化分量小1~2个数量级[3],因此对测量精度有较高要求,其中天线交叉极化对全极化微波辐射计测量精度带来的影响不可忽视。针对相关型全极化微波辐射计,本文通过建立交叉极化传输模型,引入极化纯度[4]指标,对由天线交叉极化引入的Stokes参数测量误差进行了深入分析,明确了相关型全极化微波辐射计达到测量精度时天线极化纯度须满足的指标。同时,根据误差测量原理,引入不确定度概念,仿真分析了极化纯度测量不确定度对Stokes参数测量准确度造成的影响,提出了对极化纯度指标测量精度的要求。
1 非理想天线特性下Stokes参数模型
(1)


(2)
(3)
其中,iV(iH)为水平(垂直)端口泄露到垂直(水平)端口的信号;φV(φV)为水平(垂直)端口泄露到垂直(水平)端口信号相位。则有

(4)
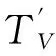

(5)

利用相关测量法测量T3、T4分量,在非理想条件下,得到T3、T4分量测量值分别为

(6)

(7)
2 极化隔离度对Stokes参数影响
造成极化泄露的原因可能是抛物面天线本身的特性、正交极化隔离器不完美,或是目标场景与天线视轴坐标基准失配[8],对比式(6)和式(7)发现,T3分量对极化纯度指标的要求比T4分量更高。图1(a)中所示为T3分量误差随着相对相位变化,可以看出,图形关于0°对称,0°、45°、90°的3个相对相位给T3分量造成误差可代表所有相对相位下T3分量的误差。为了更清楚地看到T3分量随着极化纯度变化而变化的情况,选取0°、45°、90°的3个相对相位即可。

图1 相关变化曲线
图1(b)中,横坐标是V和H极化端口的极化纯度,纵坐标是T3分量测量误差,图中3条线分别代表0°、45°、90°的3个相对相位的不同情况。从图1(b)中可看出,即使极化纯度指标很高,在不同的相对相位下,T3分量依然有2~6 K的误差存在,这个误差和T3本身相当,因此,需要对辐射计加以严格校正,以获取较为准确的T3值。
式(4)~式(7)描述了Stokes参数真实值到测量值的线性变换关系,定义矩阵变换矩阵Rcoh,则有
(8)

在式(8)中,在完成仪器定标后,若是准确测得矩阵R,则经过反演可准确得出目标场景亮温真实值。然而,R矩阵很难准确获得,测量不确定度的存在使R矩阵产生偏差,从而影响真实亮温的反演结果。
3 Stokes参数测量准确度
一般而言,R矩阵误差来源有两个:一是不可能准确测得每个参数,受限于测试条件和方法,各参数的测量总会存在一定的不确定度;二是隔离度和相对相位在测试过程中会发生漂移。这里用标准差σ表征测量不确定度。以下分析考虑完成仪器定标后,相对相位分别为0°、45°以及90°3种不同的情况,同时,极化纯度变化范围为10~50 dB。
图2所示为T3分量不确定度随着极化纯度的变化,假设图2(a)极化纯度不确定度为-40、-50 dB、相对相位确切已知图2(b)极化隔离度确切已知、相对相位不确定度为5°。首先,考虑极化纯度存在一定不确定度时T3分量的测量不确定度,如图2(a)所示,不确定度为-50 dB时,T3分量误差明显小于不确定度为-40 dB时的误差,在任意极化隔离度下这种差别都很明显。此外,当极化隔离度水平和其不确定度相当时,T3分量的误差趋于平稳,不再随着极化隔离度变化而变化,可以这样理解:假设极化隔离度不确定度为-40 dB,则隔离度本身是-40或是-50 dB已无差别,因为此时主要测量误差是由其不确定度引起的。最后,V、H通道相对相位对T3分量误差也有一定的影响。图3为极化隔离度不确定度为-40 dB、-50 dB、相对相位不确定为5°时Stokes参数T3、T4分量的不确定度。在图3(a)中,T3分量的标准差对V、H极化通道相对相位很敏感:当极化隔离度<30 dB(iV,iH<30 dB)时,相对相位为0的情况下,定标精度最好;当极化隔离度变得更小(iV,iH<20 dB)时,在相对相位为0的情况下,极化隔离度为-40 dB还是-50 dB对T3分量影响已无差别了;随着极化隔离度变好,不确定度为-50 dB则明显优于不确定度为-40 dB的情况;当极化隔离度达到一定的水平(约40 dB)时,T3分量不确定度已对极化隔离度不敏感了,这表明此时定标误差主要是由极化隔离度不确定度造成的,-50 dB不确定度对T3分量准确定标具有更明显的优势。最后,相对相位为0的情况下,当极化隔离度为20 dB时,T3分量不确定度达到最小。T4分量相对T3分量而言,其不确定度和相对相位的关系不如T3分量紧密。相对相位为0情况下,T3分量在隔离度不理想(iV,iH<20 dB)时有很好的定标精度,而T4分量则定标精度较差。图3可看出,T3、T4分量定标精度要达到0.4 k以下较为困难,除非极化纯度不确定度在足够低的水平。

图2 T3分量不确定度随着极化纯度的变化
由图2(b)可以看出,T3分量的不确定度随着极化隔离度增大而减小,这和图2(a)所示情况正好相反。实际上,无论是相对相位还是极化隔离度均不会精确已知。因此,这两个因素共同引起的T3分量不确定度变化需要加以考虑,这里认为相对相位和极化隔离度是两个不相关的分量。极化隔离度不确定度和相对相位不确定度对σT3的作用是相反的,因此,当这两个相互矛盾的因素在某个点平衡时,T3分量的不确定度σT3会达到最小。最后,注意到 与相对相位的大小有关系,其能达到的最小值依赖于相对相位的大小。

图3 T3、T4分量不确定度随极化隔离度的变化
图3为极化隔离度不确定度为-40 Db、-50 dB、相对相位不确定为5°时Stokes参数T3、T4分量的不确定度。在图3(a)中,T3分量的标准差对V、H极化通道相对相位很敏感:当极化隔离度<30 dB(iV,iH<30 dB)时,相对相位为0的情况下,定标精度最好;当极化隔离度变得更小(iV,iH<20 dB)时,在相对相位为0的情况下,极化隔离度为-40 dB还是-50 dB对T3分量影响已无差别了;随着极化隔离度变好,不确定度为-50 dB则明显优于不确定度为-40 dB的情况;当极化隔离度达到一定的水平(约40 dB)时,T3分量不确定度已经对极化隔离度不敏感,这表明此时定标误差主要是由极化隔离度不确定度造成的,-50 dB不确定度对T3分量准确定标具有更明显的优势。最后,相对相位为0的情况下,当极化隔离度为20 dB时,T3分量不确定度达到最小。T4分量相对T3分量来说,其不确定度和相对相位的关系不如T3分量紧密。相对相位为0情况下,T3分量在隔离度不理想(iV,iH<20 dB)时有很好的定标精度,而T4分量则定标精度较差。图3可看出,T3、T4分量定标精度要达到0.4 K以下是较为困难的,除非极化纯度不确定度在足够低的水平。

图4 T3 、T4分量不确定度随着极化隔离度不确定度的变化
图4 极化隔离度为30 dB、相对相位不确定为5°T3、T4分量不确定度随着极化隔离度不确定度的变化。从图4可以看出,对于T3分量来说,要使天线交叉极化定标精度<0.4 K需要极化隔离度不确定度优于-42 dB且相对相位为0,在其他的相对相位下,要达到要求的定标精度则需要更高的测量不确定度。对于T4分量,在图4(b)的仿真结果中,测量精度<0.4k需要极化隔离度达到39 dB以上。

图5 T3 、T4误差随着V、H通道相对相位不确定度的变化
图5所示极化隔离度固定为30 dB,其不确定度为40 dB。T3、T4分量误差随着V、H通道相对相位不确定度的变化。图5中,T3、T4分量的误差都随着相对相位不确定度增大而变大。在相对相位变大的过程中,T3分量误差随之增大,T4分量则与T3分量相反,其不确定度随着相对相位增大而变小。图5(a)中,相对相位为0时,T3分量误差无法达到0.4 K的要求,当相对相位变为90°时,极化隔离度水平已不是造成T3分量误差的主要因素,此时相对相位不确定度为1°时则会使T3误差分量满足<0. 4 K要求。图5(b)中,相对相位为0、不确定度为2°时,T4分量测量值可达到0.4 K的精度要求。
4 结束语
以上对相关型全极化微波辐射计极化纯度、相对相位及其不确定度对T3、T4分量的影响作了分析,为全极化微波辐射计天线子系统的设计提供了一定的指导准则。天线子系统包含主反射器、馈源以及正交转换器,这些硬件性能都会影响Stokes参数测量值与Stokes参数真实值之间的耦合程度。对硬件性能要求可分为两大类:(1)硬件本身应达到的指标;(2)实际硬件性能表现的不确定度[9]。第一类要求影响天线系统最初的整体性能,比如极化纯度隔离度必须达到一定的水平,V、H通道的相对相位必须是一定范围之内的某个值;第二类要求影响一系列设计问题和定标问题。首先,对不确定度的要求,决定了对某个参数实际测量精确度的需求,其次,决定了某个参数允许漂移的量值[10]。对不确定度的要求会影响最初对天线子系统各个参数的选择,例如,天线交叉极化隔离度差一些,可提高对其值稳定度的要求来满足测量精度。
在相关型全极化微波辐射计中,有两个定标误差共同影响极化隔离度指标的选择。一是极化隔离度不确定度对T3分量的影响随着极化隔离度增大而增大,二是相对相位不确定度对T3分量影响随着极化隔离度增大而减小。要使定标误差达到最小,极化隔离度的选择随着相对相位及其不确定度的变化而变化[11]。在所有的情况下,无论是极化隔离度还是相对相位,更好的不确定度会带来更好的定标精度。这样的因果关系可指导天线子系统设计时,在极化隔离度及其不确定度之间的选择上进行折中[12]。此外,还应注意,若要获得好的定标精度,T4分量对极化隔离度和相对相位的要求与T3分量并不一致。因此,对于全极化微波辐射计天线子系统[13-15]这样一个涉及参数较多的系统来说,要使T3、T4分量的测量精度同时满足要求,在天线参数的选择上必须全面考虑。
[1] 王振占.海面风场全极化微波辐射测量—原理、系统设计与模拟研究[D].北京:中国科学院空间科学与应用研究中心,2005.
[2] Hudson, D, Piepmeier J R, Long D G. Polarization rotation correction in radiometry: an error analysis[J]. Genes Chromosomes & Cancer, 1996, 15(3):157-164.
[3] 高晓萍.全极化微波辐射计海面风场测量的反演及精度分析[D].武汉:华中科技大学,2012.
[4] C Ruf.Constraints on the polarization purity of a Stokes microwave radiometer[J].Radio Science,1998, 33(6):1617-1639.
[5] Piepmeier J R, Long D G, Njoku E G. Stokes antenna temperatures[J]. IEEE Transactions on Geoscience & Remote Sensing,2008,46(2):516-527.
[6] Skou N B,Laursenand S Sobjerg.Polarimetric radiometer configurations: potential accuracy and sensitivity[J].IEEE Transactions on Geoscience Remote Sensing,1999,37(5):2165-2171.
[7] Ko H C.On the reception of quasi-monochromatic, partially polarized radio waves[J].Proceeding of IRE,1962,50(9):1950-1957.
[8] Njoku E G,Christensen E J, Cofield R E.The seasat scanning multichannel microwave radiometer(SMMR):antenna pattern corrections-development and implementation[J]. IEEE Journal of Oceanic Engineering, 1980, 5(2):125-137.
[9] 王振占,姜景山,刘璟怡,等.全极化微波辐射计遥感海面风场的关键技术和科学问题[J].中国工程科学,2008,10(6):76-86.
[10] Ulaby F T,Moore R K,Fung A K.Microwave remote sensing: active and passive[M].Massachusetts:Addison-Wesley Publishing Company,1981.
[11] Dzura M,Etkin V S,Khrupin A S,et al.Radiometers- polarimeters: principles of design and application for sea surface microwave emission polarimetry[C].Houston, Texas,USA:Proceeding of 1992 IEEE International Geoscience Remote Sensing Symposium,1992.
[12] 刘璟怡.全极化微波辐射计定标和风场反演若干问题研究[D].北京:中国科学院研究生院,2007.
[13] 王蕊,史顺文,陆文.全极化微波辐射计海面风场反演实验[J].遥感信息,2014(4):85-90.
[14] Windy Lippincott,Ted Gutwein,Peter Gaiser, et al. Antenna design, modeling, and testing on the windsat satellite wind derection measurement system[R].Washington DC,USA:Naval Research Laboratory,2002.
[15] Eni G Njoku,Edward J Christensen, Richard E Cofield. The seasat scanning multichannel microwave radiometer (SMMR): antenna pattern corrections-development and implementation[J]. IEEE Journal of Oceanic Engineering,1980,5(2):125-137.
Study on Polarization Purity of Polarimetric Microwave Radiometer
XING Yan ,CHEN Wenxin
(Xi’an Institute of Space Radio Technology, Xi’an 710100, China)
Measurement of the third and fourth Stokes parameters of microwave radiometer can be degraded by the level of polarization purity and the knowledge of polarization impurity. An explicit relationship is developed between the true Stokes parameters and the measurements, as functions of nonideal polarization characteristics. In principle, knowledge of the characteristics allows the degradation to be removed by a postprocessing calibration procedure. However, errors in the knowledge are possible, resulting from inexact initial testing and/or subsequent drifting of the instrument. The effects of these errors on overall calibration are considered. It is found that there is considerably greater tolerance to the errors when incoherent detection is used, as opposed to coherent detection. We discuss the effects on coherent polarimetric radiometer here, which lay the foundation of antenna pattern correction of polarization microwave radiometer.
polarimetric radiometer; polarization purity; uncertainty level; stokes parameters
2016- 03- 21
邢妍(1991-),女,硕士研究生。研究方向:微波遥感。陈文新(1969-),男,硕士生导师。研究方向:星载微波遥感技术。
10.16180/j.cnki.issn1007-7820.2017.01.009
TN821+.1;TP732.1
A
1007-7820(2017)01-029-05
