带宽自适应的Mean-Shift跟踪算法
2017-03-29孙玉秋胡维
孙玉秋,胡维
(长江大学信息与数学学院,湖北 荆州 434023)
黎雄
(北京师范大学数学学院,北京 100875)
带宽自适应的Mean-Shift跟踪算法
孙玉秋,胡维
(长江大学信息与数学学院,湖北 荆州 434023)
黎雄
(北京师范大学数学学院,北京 100875)
针对传统Mean-Shift目标跟踪算法在进行物体跟踪时核函数带宽不能实时更新的问题,提出了一种基于比较中心加权直方图与边缘加权直方图的巴氏相似度的带宽自适应算法。首先,手动选取需要跟踪的目标,计算目标模板的中心加权直方图与边缘加权直方图以及二者的巴氏相似度HistDist1;然后,在当前帧通过Mean-Shift迭代找到目标的中心,并计算出候选模板的边缘加权直方图以及目标模板中心加权直方图与候选模板边缘加权直方图的巴氏相似度HistDist2;最后,在设定范围内比较巴氏相似度HistDist1与HistDist2的大小,得到目标的尺寸变化情况。试验结果表明,该算法可以适应尺寸发生变化的目标跟踪,实现了核函数带宽的自适应。
带宽自适应;目标跟踪;Mean-Shift算法;巴氏相似度;核函数
Mean-Shift算法由Fukunaga于1975年提出,是一种基于密度梯度的无参数估计方法。1995年,Cheng将其引入计算机视觉领域,取得了较好的跟踪效果[1~3]。尽管Mean-Shift算法的实时性好,利于跟踪,但是当目标在运动过程中发生尺度变化时,将得到很差的跟踪结果。Mean-Shift算法不仅对目标的尺寸变化敏感,而且缺乏对模板的实时更新,并且对目标的描述仅用颜色特征,容易受背景影响[4,5]。
文献[1]用仿射变换来描述目标形状、尺寸的变化,但是运算量较大;文献[3]通过比较目标模板和候选模板的中心加权直方图与边缘加权直方图的相似度,实现跟踪窗的自动缩放。这种方法没有对相似度比较进行限制,在实际中容易造成窗口不断变小或者变大,甚至进入死循环;文献[6]分别对带宽加减Δh, 然后与h比较,选出其中Bhattacharyya系数最大的作为新的带宽h,然而这种猜测性的比较难以取得好的跟踪效果,容易造成搜索窗不断变小;文献[7]和文献[8]分别将灰度特征与边缘特征相结合,并且文献[7]应用的是模糊方法,但都对跟踪环境的要求较高;文献[9]结合SIFT特征和Kalman滤波以及Mean-Shift算法,可以取得好的跟踪效果,但是在很大程度增加了时间复杂度。
中心加权直方图可以有效的减少目标边缘背景的影响,可以准确获得目标中心。边缘加权直方图突出目标边缘的像素分布,通过比较目标的边缘加权直方图的相似度,可以有效的反映出目标的尺寸变化。就目标尺寸的变化问题,笔者提出了一种有效的更新核函数带宽算法。首先选取待跟踪的目标,用带宽h计算模板目标的中心加权直方图quc和边缘加权直方图qub,用巴氏相似度计算二者的相似系数HistDist1,并用带宽h进行Mean-Shift迭代,得到新的目标中心y;然后用带宽h和中心y,计算候选目标的边缘加权直方图pub,并与模板目标的中心加权直方图quc进行巴氏相似度计算,得到相似度系数HistDist2;最后比较kiHistDist1与HistDist2的大小,确定增大或缩小搜索窗,并以新的搜索窗对下一帧进行目标定位与跟踪。
1 Mean-Shift算法
在Mean-Shift算法跟踪过程中,通过比较核函数加权下的目标模板与候选模板的颜色直方图,使搜索窗沿梯度增大方向移动,得到新的目标位置。
1.1 目标模型
通过人工选取需要跟踪的目标作为跟踪模板,以目标的颜色分布作为目标特征,得到目标的颜色概率直方图,第u个特征值的概率为:
(1)

1.2 候选模型
类似的,在第N*帧中,计算出在上一帧的搜索窗内的像素的分布直方图,第u个特征值的概率为:
(2)
1.3 核函数
为减小目标周围背景像素的影响,实现对目标中心的强调,使用式(3)表示的凸函数作为核函数进行中心加权:
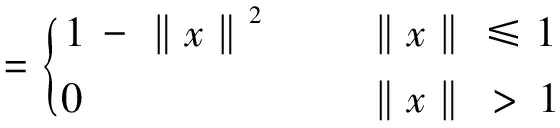
(3)
同样,为展示目标在移动时边缘像素发生的变化,使用式(4)表示的凹函数作为核函数对目标进行边缘加权:

(4)
核函数示意图如图1所示。

图1 核函数示意图
1.4 巴氏相似度(Bhattacharyya系数)
巴氏相似度由统计学家Bhattacharyya提出,是一种用来计算2个离散或连续概率分布的相似性的方法,是向量相似度匹配中最常用的算法。直方图qu与pu的相似度计算公式如下:
(5)
根据巴氏相似度计算模板目标中心加权直方图与边缘加权直方图的相似度HistDist1, 同理计算模板目标中心加权直方图与候选目标边缘加权直方图的相似度HistDist2。
1.5 Mean-Shift目标跟踪
在算法实现过程中,分别用式(1)和式(2)表示模板目标和候选目标,用Bhattacharyya系数ρ表示他们之间的匹配程度:
(6)
在初始帧,手动选取需要跟踪的目标,得到目标初始中心位置y0,在之后的每一帧,用式(7)进行迭代得到目标新的中心,实现目标的跟踪:
(7)

然而,在实际应用中,目标的尺寸通常是变化的,如果不实时更新跟踪窗带宽,将会跟丢目标。
2 基于巴氏相似度的核带宽更新
通过计算目标模板自身的中心加权直方图与边缘加权直方图的巴氏相似度以及目标模板的中心加权直方图和候选模板的边缘加权直方图的巴氏相似度,并且在设定范围内比较这2个相似度的大小,从而实现核函数带宽的实时更新。
2.1 边缘加权与中心加权

事实上,模板目标自身中心加权直方图与自身边缘加权直方图的相似度,多数情况大于模板目标中心加权直方图与候选目标边缘加权直方图的相似度。见表1。其中,HistDist1为目标模板的中心加权直方图与自身的边缘加权直方图的相似度;HistDist2为目标模板的中心加权直方图与下一帧的边缘加权直方图的相似度;HistDist3为目标的中心加权直方图与下一帧的搜索窗缩小的边缘加权直方图的相似度;HistDist4为目标的中心加权直方图与下一帧的搜索窗变大的边缘加权直方图的相似度。

表1 相似度大小变化情况
注:Hi即为文中的HistDisti。
比较表1的H1和H2可以看出,目标模板的中心加权直方图与自身的边缘加权直方图之间的相似度,几乎远大于目标模板的中心加权直方图与下一帧的边缘加权直方图的相似度。比较H3和H4可以看出,当搜索窗缩小时,相比于HistDist2(即搜索窗大小不变时),相似度变小;当搜索窗变大时,相似度变大。根据这一变化规律可以确定目标的缩放情况。
2.2 带宽自适应算法实现
由于在多数情况下,HistDist1 一定大于HistDist2,因此,在比较两者大小关系时,需要加上一个比例系数k,即,如果kHistDist1 图2 中心加权直方图与边缘加权直方图 当目标尺寸发生大小变化时,搜索窗应当保持同等大小的变化。如果kHistDist1 1) 读取视频文件,选取待跟踪的目标,用带宽h计算模板目标的中心加权直方图quc和边缘加权直方图qub,用巴氏相似度计算二者的相似系数HistDist1; 2) 在当前帧,用带宽h进行Mean-Shift迭代,得到新的目标中心y; 3) 用带宽h和中心y,计算候选目标的边缘加权直方图pub,并与模板目标的中心加权直方图quc进行巴氏相似度计算,得到相似度系数HistDist2; 4) 比较kiHistDist1与HistDist2的大小,如果k1HistDist1 5) 用新的带宽h和新的目标中心y对下一帧进行目标定位与跟踪。 图3 带宽自适应目标跟踪算法流程图 对实时车辆的跟踪结果如图4所示,其中红色方框为搜索框,蓝色线条为跟踪轨迹;最左侧一列为目标尺寸变小的情况,车辆由近至远逐渐变小;右侧为目标尺寸变大的情况,车辆由远到近尺寸逐渐变大。由图4可以看出,对于这2种情况,笔者提出的算法都能够实时准确的检测并标出目标所在位置,实现了搜索窗的大小随着目标尺寸变化而自动变化。因此,相比于传统Mean-Shift跟踪算法在跟踪过程中搜索窗大小不变的情况,该算法可以自动适应跟踪目标的尺寸变化,并且能够实现核函数带宽的实时更新,有更好的跟踪效果。 笔者提出的算法通过结合目标的中心加权直方图与边缘加权直方图,并且对目标模板与候选模板的比较进行系数限制,可以很好的满足并且适应目标尺寸发生的变化。相比于文献[1]的仿射变换,该算法计算量更少,更能适应实时跟踪的要求。相比于文献[3]直接比较中心加权直方图与边缘加权直方图,文献[6]猜测性的选取核函数带宽,该算法有效解决了核函数带宽在一些情况下只能变小以至于搜索窗不断缩小的问题;相比于文献[7]和[8],算法对环境的要求降低;相比于文献[9],算法在时间复杂度上更有优势。 传统Mean-Shift跟踪算法以直方图作为目标特征,并且缺乏模板更新,带宽大小不变。笔者提出的算法基于传统的Mean-Shift跟踪算法,改进了传统算法带宽不变的缺点,实现了跟踪的带宽自适应。在试验过程中发现,在更新带宽的过程中,同时对搜索窗的长和宽进行同比例缩放,当目标的长宽比例发生变化时,可能跟丢目标;对于速度过快的目标,传统的目标跟踪算法搜索窗中心的更新跟不上目标的移动。后期对这个方向的进一步研究将会有重大意义。 [1]朱胜利,朱善安. 核函数带宽自适应的Mean-Shift目标跟踪算法[J].光电工程, 2006, 33(8): 0011~0016. [2]ChengY.Meanshift,modeseeking,andclustering[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1995, 17(8): 790~799. [3]陈昌涛, 朱勤, 周圣毅, 等. 核函数带宽自适应的Mean-Shift跟踪算法[J].计算机应用, 2009, 29(6): 1680~1682. [4]ZhangHuanqing,GeHongwei,YangJinlong.AdaptiveGaussianmixtureprobabilityhypothesisdensityfortrackingmultipletargets[J].Optik, 2016, 127: 3918~3924. [5]YanZouguo,LiangWeiguo,LvHaidong.ATargetTrackingAlgorithmBasedonImprovedCamshiftandUKF[J].SoftwareEngineeringandApplications, 2014, 7: 1065~1073. [6]ComaniciuD,RameshV,MeerP.Kernel-BasedObjectTracking[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2003, 25(5): 665~676. [7]XiaoGang,YunXiao,WuJianMin.Amulti-cuemean-shifttargettrackingapproachbasedonfuzzifiedregiondynamicimagefusion[J].ScienceChina, 2012, 3(55): 577~589. [8]ZhengHaichao,MaoXia,ChenLijiang,etal.Adaptiveedge-basedmeanshiftfordrasticchangegraytargettracking[J].Optik, 2015, 126: 3859~3867. [9]朱志玲, 阮秋琦. 结合尺度不变特征变换和Kalman滤波的MeanShift视频运动目标跟踪[J].计算机应用, 2013, 33(11): 3179~3243. [编辑] 洪云飞 2016-11-05 国家自然科学基金项目(11571041);湖北省自然科学基金资助项目(2013CFA053)。 孙玉秋(1968-),女,博士,教授,博士生导师,现主要从事数字图像处理、模式识别与目标检测方面的教学与研究工作,yqsun@yangtzeu.edu.cn。 TP391 A 1673-1409(2017)01-0005-07 [引著格式]孙玉秋,胡维,黎雄.带宽自适应的Mean-Shift跟踪算法[J].长江大学学报(自科版),2017,14(1):5~11.

3 试验结果分析
4 结语
