基于误差采样的Nyström谱聚类图像分割算法研究
2017-03-29刘仲民李博皓李战明胡文瑾
刘仲民,李博皓,李战明,胡文瑾
(1.兰州理工大学 电气工程与信息工程学院,甘肃 兰州730050;2.西北民族大学 数学与计算机学院,甘肃 兰州730000)
基于误差采样的Nyström谱聚类图像分割算法研究
刘仲民1,李博皓1,李战明1,胡文瑾2
(1.兰州理工大学 电气工程与信息工程学院,甘肃 兰州730050;2.西北民族大学 数学与计算机学院,甘肃 兰州730000)
谱聚类算法在聚类过程中要计算样本相似度矩阵,构造数据量大,并且要对拉普拉斯矩阵进行特征分解,计算比较耗时。Nyström扩展方法通过部分采样数据来逼近原始特征空间,可以有效降低谱聚类算法的计算复杂度。采样点的选择是决定Nyström扩展方法精度的重要因素,通过对Nyström扩展方法的误差进行分析,结合图像特征信息,设计了一种新的采样方案。利用均匀采样方法对图像进行初步采样,并通过迭代的方法最小化采样点与像素点之间的误差,得到最终采样点特征值。通过在Berkeley图库上的图像分割实验表明了算法的可行性和有效性。
Nyström;谱聚类;图像分割;K均值
0 引言
图像分割就是指把图像分成各具特性的区域并提取出感兴趣目标区域的技术和过程[1]。它是计算机视觉处理中极为重要的环节之一,是由图像处理进入到图像分析的关键步骤[2]。谱聚类是一种新型聚类分析方法,具有能够处理任意形状的数据集、易于执行等优点[3]。近些年来谱聚类算法得到了迅速发展,并被应用于图像分割及其相关领域。
在图像分割中,谱聚类计算像素点之间的相似度矩阵并求解该矩阵的特征值与特征向量,通过对特征向量进行聚类完成对图像的划分。谱聚类算法将图像划分为多个区域,使得同一区域内部像素点相似度高,不同区域之间相似度低,获得了较好的分割效果[4]。然而,谱聚类算法计算过程中产生的相似度矩阵规模过大,特征值与特征向量的存储、计算使得谱聚类算法计算复杂度过高[5]。例如:一幅像素数目为n、特征维度为d的图像,计算其相似度矩阵的时间复杂度高达O(d2n2),空间复杂度高达O(n2),拉普拉斯矩阵特征分解的时间复杂度更是高达O(n3)。
谱聚类的计算复杂度过高严重制约了其在图像分割方面的应用。对此,国内外学者对其进行了一系列的研究和改进,其中Nyström扩展方法[6]是应用和研究较多的一种改进方法。Nyström扩展方法可以使用小部分数据近似逼近整个数据集的相似度矩阵和其特征空间,从而降低了谱聚类对时空的要求。文献[7]最初将Nyström扩展方法应用在谱聚类中,并以此成功地进行了图像分割。文献[8-9]在文献[7]的基础上对Nyström扩展的逼近误差进行了详细的理论分析,提出了基于K均值采样的Nyström算法。但在图像分割中K均值采样算法存在两点不足:① 无法准确预估像素各特征值之间的权重;② 采样点较多时,K均值聚类运算速度较慢。
针对以上问题,本文提出了一种基于最小误差采样的Nyström谱聚类算法。经实验验证,该算法在分割有效性上相对于传统Nyström谱聚类算法有显著提高。
1 谱聚类及其改进算法
1.1 谱聚类算法
谱聚类是一种基于图论的聚类方法。图由若干点及连接两点的线构成,用点代表事物,线表示对应2个事物间具有的某种关系,又称为权重。将图划分为若干个子图,各子图无交集,划分时子图之间被“截断”的边的权重和称为损失函数[10]。谱聚类通过最小化损失函数来实现图的划分[11]。
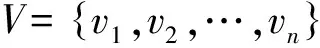

(1)
损失函数:

(2)

(3)
式中,W为权重矩阵;D为对角矩阵。
(4)
定义拉普拉斯矩阵L=D-W,将最小化损失函数的问题转化为最小化qTLq的问题[12]。
1.2 基于Nyström的谱聚类算法
谱聚类通过最小化qTLq实现聚类划分,qTLq的最小值在q为L的次小特征值对应的特征向量时实现。对L进行特征分解运算量巨大,文献[13]利用Nyström扩展方法求得特征向量的近似值。

(5)
式中,P(y)为核密度函数;k(x,y)为正定的核函数;λi为特征值;Φi为特征向量。

(6)

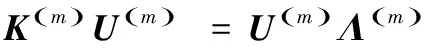
(7)

(8)
对于非连续核密度函数,设数据集X={x1,x2,…,xn},相似度矩阵K,采样点集Z={z1,z2,…,zm},采样相似度矩阵W,则K的特征值和特征向量分别为:
(9)
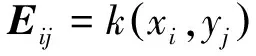
(10)
2 最小误差采样的Nyström方法
Nyström扩展方法提高了谱聚类算法的运算效率,但是如果得到的相似度矩阵与原相似度矩阵误差过大会影响图像的分割效果[14]。本文通过对相似度矩阵误差进行分析,并选择最小化误差的采样方法完成谱聚类图像分割。
2.1 最小误差分析
本文所取相似度矩阵函数为高斯核函数[15],由中值定理可知存在C使其满足:
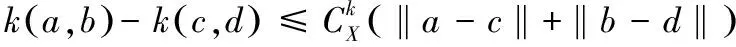
(11)

相似度矩阵误差为:
ε=‖K-EW-1ET‖F。
(12)
对于单独数据点来说,
εIi,Ij=‖KIi,Ij-EIi,ZW-1EIj,ZT‖F。
(13)

AIi,Ij=KIi,Ij-Wpq,
BIi,Z=EIi,Z-WpZ,
CIj,Z=EIj,Z-WqZ。
(14)



(15)

(16)
从以上推导可以看出Nyström方法最终误差大小由采样数目、采样相似度矩阵以及数据点与最近的采样点误差决定。
2.2 最小误差采样算法
对Nyström扩展方法进行误差分析,发现在图像分割中,采样数目与相似度函数不变的情况下,可以通过最小化像素点与采样点误差对最终误差进行优化。
本文选取图像为灰度图像,3个特征值分别为坐标x坐标、y坐标和灰度值I(x,y)。对灰度图像进行采样必须保证式(17)最小化。

(17)
式中,εx,y为坐标误差;εI(x,y)为灰度值误差。具体采样步骤如下:
输入:给定图像I,像素个数n,特征中心个数m,终止迭代参数σ。
输出:特征中心Q。
步骤 1:按照设定的采样点个数m,在图像I上进行均匀采样,并将像素分配到与之最近的采样点;
步骤2:计算采样点3×3邻域内像素点的灰度梯度值,选取梯度值最小的点作为新的采样点;
步骤3:设置步长S=(nm)1/2,在2S×2S邻域内按照距离:
d=dx,y+dI(x,y),
(18)
为每一个采样点分配像素。其中dx,y为坐标的欧氏距离,dI(x,y)为灰度差的绝对值。
步骤4:求取采样点所属像素的平均值作为新的采样点Q,计算新旧采样点误差:

(19)
如果ε<σ转步骤5;否则转步骤3;
步骤5:输出Q作为区域特征中心。
从算法流程可以看出,算法的关键在于对数据点的选取时充分利用像素点与采样中心之间的距离关系,使得误差最小化。根据K均值聚类算法可得知,通过步骤1在空间上进行均匀采样可得到最小化的εx,y。利用步骤2可以防止采样点落在噪音或者边界上。在此基础上,步骤3和步骤4计算每个采样中心拥有像素的灰度值,并在一定范围内变化像素点所属采样中心,并更新采样中心坐标,利用迭代的方式最小化灰度值误差εI(x,y)。
基于以上表述,改进的谱聚类算法步骤如下[16]:
步骤1:将图像按照本文算法进行采样,利用高斯函数构建采样相似度矩阵W,采样点与像素点的相似度矩阵E;
步骤2:通过Nyström方法估算出特征值与特征向量,将特征值由大到小排序后,选择前k最小的特征值所对应的特征向量,用矩阵V表示;
步骤3:将矩阵V进行归一化,并记归一化的矩阵为Y:

(20)
步骤4:矩阵Y的每行视为样本,运用K均值聚类算法将它们聚为k类;
步骤5:确定原像素点归属类别,完成图像分割。
3 实验结果与有效性分析
为了检验该算法的性能,对文中所述算法进行了实验分析。实验环境为Windows10系统、Inteli3处理器、4GB内存,实验平台MATLAB7.0。实验图像来源于Berkeley图库。实验中对每幅图像抽取m=100的像素点。
图1为图像数据库中3幅原始图像。图2为随机采样Nyström谱聚类分割结果。图3为本文算法分割结果。图4为人工分割结果。

图1 原始图像

图2 随机采样Nyström谱聚类分割结果

图3 本文算法分割结果
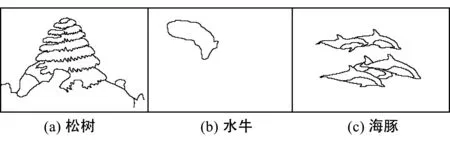
图4 人工分割结果
通过对比发现,在对图1(a)~图4(a)的松树图像的分割中,随机采样Nyström谱聚类分割将背景中与松塔灰度值接近的区域与目标划分在一起,而本文提出的改进算法能准确地将目标区域分割出来。对图1(b)~图4(b)的水牛以及图1(c)~图4(c)的海豚图像的分割中,由于图像背景复杂,传统分割方法效果很不理想。不仅存在大量噪点,而且存在误分割区域。而本文算法可以更清楚地观察到分割轮廓和图像细节的对应情况,明显将水牛与海豚同背景区分开来,其分割效果与人工分割结果基本一致。
4 结束语
本文基于采样误差分析,通过最小化像素与最邻近采样点之间误差对Nyström谱聚类图像分割方法进行了优化。首先在全局范围内均匀采样,最小化坐标之间的误差;其次在局部范围内利用迭代算法最小化灰度值误差,最终找到最优的采样中心,使得本文算法运算过程中所得相似度矩阵能更真实的反映图像信息。通过对Berkeley图库标准测试图片进行分割验证了本算法的有效性。
[1] 章毓晋.图像分割中基于过渡区技术的统计调查[J].计算机辅助设计与图形学学报, 2015,27(3):379-381.
[2]ZHUZ,WANGL.InitializationApproachforFuzzyCmeansAlgorithmforColorImageSegmentation[J].ApplicationResearchofComputers,2015,32(4):1 257-1 260.
[3] 苏木亚,郭崇慧.基于主成分分析的单变量时间序列聚类方法[J].运筹与管理,2011(6):66-72.
[4] 田 玲,邓旌波.基于多空间多层次谱聚类的非监督SAR图像分割算法[J].计算机应用研究,2013,30(7):2 213-2 215.
[5] 蔡晓妍,戴冠中,杨黎斌.谱聚类算法综述[J].计算机科学,2008,35(7):14-18.
[6] 阳 春,张向荣,焦李成.结合Nyström逼近的图半监督纹理图像分割[J].系统工程与电子技术,2009,31(12):2 820-2 825.
[7]FOWLKESC,BELONGIES,CHUNGF,etal.SpectralGroupingUsingNyströmExtension[J].IEEETransactionsonPatternAnalysisandMachineIntel1igencc,2004,26(2):214-225.
[8]ZHANGK,TSANGIW,KWOKJT.ImprovedNyströmLow-rankApproximationandErrorAnalysis[C]∥InProceedingsofthe25thInternationalConferenceonMachineLearning,Helsinki,2008:1 232-1 239.
[9]ZHANGK,KWOKJT.ClusteredNyströmMethodforLargeScaleManifoldLearningandDimensionReduction[J].JEEETransactionsonNeuralNetworks,2010,21(10):1 576-1 587.
[10] 吴 健,崔志明,时玉杰,等.基于局部密度构造相似矩阵的谱聚类算法[J].通信学报,2013(3):14-22.
[11]WANGS,GUJ,CHENF.ClusteringHigh-DimensionalDataviaSpectralClusteringUsingCollaborativeRepresentationCoefficients[M].IntelligentComputingTheoriesandMethodologies.SpringerInternationalPublishing,2015:248-258.
[12] 侯 叶,郭宝龙.基于图论的运动对象分割[J].吉林大学学报(工学版),2008,38(4):902-906.
[13]CHENZ,QIUZ,LIJ,etal.Two-derivativeRunge-Kutta-NyströmMethodsforSecond-orderOrdinaryDifferentialEquations[C]∥NumericalAlgorithms,2015:1-31.
[14] 唐文俊,左亚尧,张 波,等.一种基于密度聚类Nyström抽样算法[J].计算机工程与科学,2012,34(11):148-152.
[15]LUZ.ConstrainedSpectralClusteringthroughAffinityPropagation[C]∥IEEEConferenceonComputerVisionandPatternRecognition,2008:1-8.
[16] 印世乐,曾志勇.一种改进的Nyström谱聚类图像分割算法[J].计算机与现代化,2014(4):20-23.
刘仲民 男,(1978—),副教授,博士研究生。主要研究方向:机器视觉、智能信息处理与模式识别。
李博皓 男,(1990—),硕士研究生。主要研究方向:智能信息处理与模式识别。
Error Sampling Based Nyström Spectral Clustering Image Segmentation
LIU Zhong-min1,LI Bo-hao1,LI Zhan-ming1,HU Wen-jin2
(1.CollegeofElectricalandInformationEngineering,LanzhouUniversityofTechnology,LanzhouGansu730050,China; 2.CollegeofMathematicandInformationTechnology,NorthwestUniversityforNationalities,LanzhouGansu730000,China)
Spectral clustering is based on the similarity of data,but the similarity matrix is complex,and the calculation process of Laplacian characteristic decomposition is very time-consuming.The Nyström extension method approximates the original feature space by sampling,which reduces the computational complexity of spectral clustering effectively.A new sampling method is presented in this paper,which is based on the features of image and Nyström error analysis.First,uniform sampling is used to generate a set of cluster centers;then,the error between data and centers is minimized by iteration.Finally,experiments verify the feasibility and effectiveness of the method.
Nyström;spectral clustering;image segmentation;k-means
10.3969/j.issn.1003-3106.2017.04.05
刘仲民,李博皓,李战明,等.基于误差采样的Nyström谱聚类图像分割算法研究[J].无线电工程,2017,47(4):20-23.
2017-01-06
国家自然科学基金资助项目 (64561042)。
TP391
A
1003-3106(2017)04-0020-04
