基于强跟踪滤波器的机动航天器跟踪定位

陈韬亦，马鹏斌，李江红

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.清华大学 航天航空学院，北京 100084；3.宇航动力学国家重点实验室 西安卫星测控中心，陕西 西安 710043；4.西北工业大学 动力与能源学院，陕西 西安 710072)

基于强跟踪滤波器的机动航天器跟踪定位

陈韬亦1，马鹏斌2,3，李江红4

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.清华大学 航天航空学院，北京 100084；3.宇航动力学国家重点实验室 西安卫星测控中心，陕西 西安 710043；4.西北工业大学 动力与能源学院，陕西 西安 710072)

针对雷达测量跟踪有轨道机动的非合作航天器的定位和轨道计算问题，在EKF的基础上引入强跟踪滤波器，采用增广的航天器轨道动力学模型，估计推力加速度。在航天器进行轨道机动时，滤波器自身可完成对轨道机动的快速判断和检测，滤波过程无需额外的检测手段，通用性高，可适用于针对非合作空间目标的轨道计算和跟踪与定位。数值仿真表明，对雷达数据，轨道机动约10 s后即可检测出发生了轨道机，位置精度在几十m量级，速度精度在0.1 m/s量级。

强跟踪滤波器；非合作雷达测量；轨道计算

0 引言

使用雷达测量跟踪和定位非合作空间目标对于空间观测和跟踪具有重要实际意义。对于航天器的轨道确定，在工程实践当中最为常用的是卡尔曼滤波器以及在卡尔曼滤波器之上发展出来的各种滤波器，如扩展卡尔曼滤波器(Extended Kalman Filter,EKF)[1]、文献[2-3]提出的无迹卡尔曼滤波(Unscented Kalman Filter,UKF)等滤波方法。而在空间飞行的航天器经常会实施的轨道机动，会对使用雷达数据进行航天器轨道计算的方法产生干扰，EKF和UKF在面对目标系统发生突变的情况时，将会失去其有效性，对于状态的估计出现发散的情况。对于轨道机动过程，国内外做过很多工作，例如，文献[4-5]对航天器推力加速度模型，建立增广的航天器轨道动力学模型，估计推力加速度。其中，对轨道机动过程的快速精确检测与判断是研究的重点。本文采用强跟踪滤波器(Strong Tracking Filter，STF)[6]，根据测量残差的正交性原理，对所估计状态量的变化有很强的跟踪能力，可以在滤波过程中快速对轨道机动进行检验，利用估计推力加速度的增广航天器轨道动力学运动模型，可对推力加速度和工作时段进行辨识。

1 动力学模型和测量模型

1.1 动力学模型

在J2000惯性系中，航天器运动方程为:

(1)

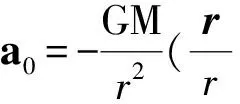
(2)

(3)

式中，F为有限连续推力的大小；m为卫星的质量；Isp为发动机比冲；g0为地面重力常数；A为推力方向矩阵，和航天器姿态和推力器安装位置相关。一般情况下，如果有限连续推力的作用时间不是很长，而且其幅值不大的话，可以认为该推力对于航天器的质量影响较小。定义RTN坐标系，R轴为径向，与地心到卫星质心的向径方向一致；T轴为横向，在轨道面内与R轴垂直，指向卫星运动方向；N轴为轨道面正法向，与R和T轴成右手系。则有限连续推力产生的加速度可以认为是一个在RTN坐标系下的常值矢量。

记位置矢量从J2000惯性坐标系到RTN坐标系的转换矩阵为G，由RTN坐标系的定义可得转换矩阵G的各元素为：

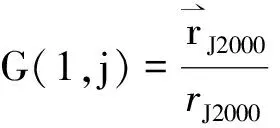
G(2,i)=G(1,j)×G(3,k)，

(4)

式中，i=1,2,3对应着转换矩阵G中每个行向量的3个分量。G(1,j)、G(2,i)和G(3,k)分别为矩阵G中第1行、第2行和第3行的行向量。

1.2 测量模型

(5)

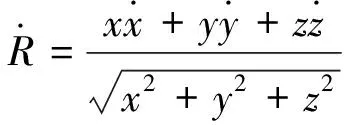
(6)

(7)

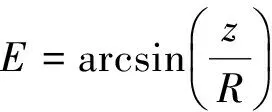
(8)

2 估计方法

2.1 EKF算法

对于航天器的实时轨道确定，在工程实际当中最为常用的是卡尔曼滤波器以及在卡尔曼滤波器之上发展出来的各种滤波器，如EKF、UKF等滤波方法，本文以EKF为例。

设状态量x为位置、速度和加速度，测量量y为测距、测速、方位角和俯仰角。设航天器的状态方程和量测方程为：

(9)

式中，w为模型噪声；R为观测噪声。线性化后的方程为：

(10)

若tk的估值为xk，协方差矩阵为Pk， 如果得到tk+1时刻的一个新观测数据为yk+1，导航算法即是tk+1时刻的估值xk+1。

EKF算法需要对方程进行线性化，基本算法如下[9]：

② 计算tk+1时刻的预测协方差矩阵：

(11)

③ 计算卡尔曼增益 ：

(12)

④ 进行状态更新：

(13)

⑤ 误差协方差矩阵更新：

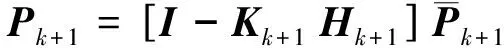
(14)

2.2 强跟踪滤波器算法

EKF和UKF序贯处理算法在面对目标系统发生突变的情况时，将会失去其有效性，出现发散的情况。

强跟踪滤波器是由周东华[10-12]于20世纪90年代提出的一种基于扩展卡尔曼滤波器的序贯处理算法。强跟踪滤波器依靠残差正交化的原理实现了在系统模型参数和过程参数失配的情况下对于系统状态的可靠估计。文献[13-16]分别对不同卫星和不同测量手段的自主导航和轨道计算，引入并采用强跟踪滤波器，取得了一定效果。

引入强跟踪滤波器，对上一节的EKF和UKF进行修改，把预报协方差矩阵改变为：

(15)

对于系数矩阵Λk+1，计算方法如下：

Λk+1=diag(λ1(k+1),λ2(k+1)，…，λn(k+1)),

(16)

(17)

(18)

N(k+1)=V0(k+1)-βR(k+1),

(19)

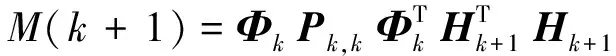
(20)

(21)

式中，ρ为遗忘因子，可设ρ=0.95；β≥1为预先选定的弱化因子，适当地增大β的值可以使估计更为平滑；αi≥1,i=1,2,…,n均为预先选定的系数。如果存在先验信息，对于变化较快的xi，可以选择一个较大的αi以提高强跟踪滤波器的跟踪能力。 如果不存在先验信息，则可以取α1=α2=…=αn=1。这样做就使基于多元渐消因子的STF退化为单渐消因子的STF，但其跟踪能力也能够保持得比较好。

2.3 基于强跟踪滤波器的机动判断方法

渐消因子λ由分子与分母两部分构成。分子项N(k+1)表征了残差在统计意义上排除掉测量误差之后的积累值，在一定程度上代表了当前一定时间步内的状态估计与实际状态之间的误差。而分母项M(k+1)表征了理论上对于状态估计误差的期望，也就可以代表状态估计误差的一个容许范围。当渐消因子λ大于1时，说明当前残差的积累程度已经大于当前状态估计的误差容许范围，就可以说明系统模型发生了未知的变化，即目标航天器受到了推力的作用。而同样的，当推力消失时，滤波器给出的状态估计将再一次偏离系统的真实状态，由残差积累产生的渐消因子也将增大到1以上。因此，可以很直观地采用渐消因子λ是否大于1这一指标来表征推力是否发生或者结束。可以用一个简单的式子来表示这一判据：

(22)

在推力产生而强跟踪滤波器的渐消因子指标λ还没有达到1的时间段内，滤波器的渐消因子呈现迅速增加的趋势。因为在这一段时间内，由于推力的作用，滤波器的状态估计正在逐渐脱离系统的实际状态值，反映在残差上就会导致残差不断偏离观测误差的范围，进而导致渐消因子λ的增大。由于观测误差始终存在，因此λ的增大并不会是单调增大的，一般情况下都是在总体增大的趋势之下进行包含有一定幅度的跳动。因此，一个很直观的想法是，在一定时间范围内对渐消因子λ进行统计，提取其变化过程的统计规律，如果判断得出在一段时间内，渐消因子在整体上是不断增加的，且其增加的幅度大于一定的值，就可以判断出此时发生了推力的产生、结束以及变化。这一种判断方法称为渐消因子变化趋势判断方法，可以表示为：

(23)

3 仿真算例

选取航天器为高度800 km的近圆轨道，地面雷达对该航天器可跟踪15 min的弧段。仿真弧段内6～9 min间航天器进行轨道机动，机动力为RTN坐标系下T向推力，加速度大小为0.02 m/s2。仿真测量数据设为0.1 s一点，对仿真的对测量数据加入误差为测距10 m，测速0.03 m/s，测角0.02°。采用强跟踪滤波器进行滤波估值，计算结果如图1、图2和图3所示。图1为位置误差，图2为速度误差，图3为加速度的估值。由图可见，轨道机动开始和轨道机动结束时，滤波器可自适应判断出推力发生了变化，并对加速度进行估值。轨道机动约10 s后即可检测出发生了轨道机动。轨道机动约100 s后，即可较为准确地估计出加速度的大小，位置速度估计值也都收敛。位置误差在几十米量级，速度误差在0.1 m/s量级。

图1 位置误差

图2 速度误差

图3 推力加速度估值

4 结束语

在实际中，一个难点在于轨道机动的检测和判别。由于渐消因子变化趋势判断方法存在着漏报的可能性，可以考虑将其与渐消因子阈值判断方法相结合，采用2种方法同时对滤波器的状态估计过程进行监视。数值仿真表明本方法的有效性，轨道机动约10 s后即可检测出发生了轨道机动，约100 s后即可较为准确地估计出加速度的大小，位置速度估计值也都收敛，位置误差在几十米量级，速度误差在0.1 m/s量级。可适用于雷达测量非合作空间目标的轨道计算。

[1] KALMAN R E, BUCY R S.New Results in Linear Filtering and Prediction Theory[J].Journal of Basic Engineering, 1961(83):95-107.

[2] JULIER S J, UHLMANN J K.New Extension of the Kalman Filter to Nonlinear Systems[J].Proceedings of the SPIE-The International Society for Optical Engineering, 1997(3068): 182-193.

[3] JULIER S J, UHLMANN J K.Unscented Filtering and Nonlinear Estimation[J].Proceedings of the IEEE, 2004, 92(3): 401-422.

[4] 李恒年, 李济生, 黄永宣.轨道机动过程推力加速度的在线最小方差估计[J].空间科学学报, 2002, 22(4):357-362.

[5] 李恒年, 祝转民, 李济生.空间机动目标的跟踪与定位[J].中国空间科学技术, 2002, 23(3):13-18.

[6] 周东华.非线性系统的自适应控制导论[M].北京: 清华大学出版社, 2002:44-49.

[7] 李济生.人造卫星精密轨道确定[M].北京：解放军出版社, 1995.

[8] 刘 林.人造地球卫星轨道力学[M].北京：高等教育出版社, 1992.

[9] BAR-ITZHACK I Y, MEDAN Y.Efficient Square Root Algorithm for Measurement Update in Kalman Filtering[J].Journal of Guidance and Control, 1983, 6(3):129-134.

[10] 周东华, 席裕庚, 张钟俊.非线性系统带次优渐消因子的扩展Kalman滤波[J].控制与决策, 1990, 5(5):1-6.[11] 周东华,席裕庚,张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991, 17(6): 689-696．

[12] 周东华, 叶银忠.现代故障诊断与容错控制[M].北京: 清华大学出版社, 2000:60-79.

[13] 叶 飚, 杨 博.一种强跟踪非线性衰减滤波的环月自主导航方法研究[J]．航天控制，2009，27(5)：23-27．

[14] 赵 欣, 王仕成, 刘志国, 等．基于强跟踪滤波的多模卫星容错导航算法[J]．现代雷达,2009,31(9):47-51．

[15] 李 丹, 刘建业, 熊 智.强跟踪滤波器在卫星紫外导航中的应用研究[J].传感器与微系统, 2008,27(9):11-13.

[16] 潘耿峰.一种基于共址滤波器解决同址多台的方法[J].移动通信,2015,39(16):67-71.

陈韬亦 男，(1984—)，博士，高级工程师。主要研究方向：航天地面系统技术。

马鹏斌 男，(1973—)，博士生，高级工程师。主要研究方向：航天器轨道计算。

Tracking and Positioning of Spacecraft Orbit Maneuver Process Based on Strong Tracking Filter Using Radar Non-cooperative Target Measurement

CHEN Tao-yi1, MA Peng-bin2,3, LI Jiang-hong4

(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China； 2.SchoolofAerospace,TsinghuaUniversity,Beijing100084,China； 3.StateKeyLaboratoryofAstronauticDynamics,Xi’anSatelliteControlCenter,Xi’anShaanxi710043,China； 4.SchoolofPowerandEnergy,NorthwesternPolytechnicalUniversity,Xi’anShaanxi710072,China)

A strong tracking filter based on EKF and UKF is used for orbit calculating during spacecraft orbit maneuvers using radar non-cooperative spacecraft measurement. The filter can detect the orbit maneuver quickly without additional detecting means. It is suitable for orbit calculating, tracking and positioning of non-cooperative spacecraft. The numerical simulation shows that by using radar measurement, the orbit maneuver can be detected after 10 s. The position accuracy is on the order of tens of meters, and the velocity accuracy is on the order of 0.1 m/s.

strong tracking filter;radar non-cooperative target measurement;orbit calculating

10.3969/j.issn.1003-3106.2017.04.09

陈韬亦,马鹏斌,李江红.基于强跟踪滤波器的机动航天器跟踪定位[J].无线电工程,2017,47(4):35-38.

2017-01-02

中国博士后科学基金一等资助项目(2015M580217)。

V448.2

A

1003-3106(2017)04-0035-04