基于LU分解的LDPC编码改进算法研究
2017-03-29高宏伟
高宏伟
(中国人民解放军第91604部队,山东 龙口 265700)
基于LU分解的LDPC编码改进算法研究
高宏伟
(中国人民解放军第91604部队,山东 龙口 265700)
为了使低密度奇偶校验码(Low Density Parity-check Code,LDPC)的校验矩阵H满足系统码的形式,同时降低校验矩阵的复杂度,减少编码时的存储空间,提出改进的优化准则,设计一种基于LU分解的算法。通过用全主元策略对校验矩阵进行高斯消元、行列交换等调整,使之具有系统码的形式,分解后得到的矩阵具有更好的稀疏性,从而可以进一步简化编码设计、减小存储空间占用和降低计算复杂度。所采用的算法与校验矩阵的构造无关,对性能无影响,且利于硬件实现,具有较好的应用前景。
校验矩阵;系统码;LU分解;低密度奇偶校验码;编码;改进算法
0 引言
20世纪60年代,Robert G.Gallager在文献[1-2]中提出了低密度奇偶校验(Low Density Parity-Check,LDPC)码。LDPC码是一种线性分组码,具有极低的错误平台[3],其性能非常接近Shannon极限,Sae-Young Chung等设计的非规则LDPC码的性能与Shannon极限仅仅相差了0.004 5 dB[4]。但由于Robert G.Gallager所提出的LDPC码既不是系统形式的也不是循环的,在编译码时复杂度非常高,限于当时的计算能力,LDPC码被认为不是实用码,在很长一段时间内没有受到人们的重视。直到1996年,随着Mackay和Neal等人的深入研究以及数字处理器件的快速发展,使LDPC码成为信道编码领域研究的热点[5]。文献[6-9]证明了不同条件下的LDPC码具有描述简单、编译码性能优越等优点,从而吸引了众多研究者的目光,并使LDPC码在多媒体广播、数字家庭网络等多种通信系统中得到应用。本文针对LDPC的编码实现,改进了LU分解方案,可以获得稀疏性更好的L、U矩阵,更加易于实现。
1 LDPC码及通用编码方法
LDPC码可由其校验矩阵定义,一个校验矩阵为Hm×n的LDPC码,其码长为n,校验位长度为m,信息位长度为m-n。此外,在分析和研究LDPC码的过程中常常使用Tanner图来表示[10],通过Tanner图可以非常直观地描述LDPC码的编译码特性。Tanner图与相应的校验矩阵直接对应,将编码后的比特用一个称为信息节点或变量节点的顶点集来表示,顶点个数等于码长。校验约束用另一个称为校验节点的顶点集来表示,顶点个数等于校验方程数。若第i个码元比特参与了第j个校验约束,则校验矩阵中的第i行第j列的元素为“1”,而在相应的信息节点和校验节点之间连一条边。一规则LDPC码的校验矩阵为:

则其相应的Tanner图表示示例如图1所示。
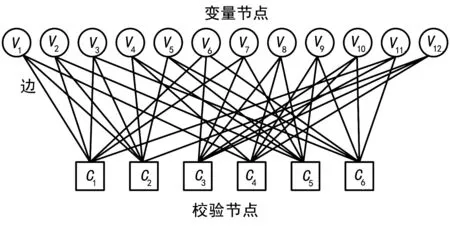
图1 LDPC码校验矩阵Tanner图表示示例
目前,在LDPC码的研究上,相对于译码方面所取得的成果来说,编码方面的进展不快,还没有找到一种好的通用方法。现有的LDPC编码方法一般可分为随机化方法和结构化方法。从纠错性能和实现复杂度两方面考虑,随机化方法的纠错性能较好但实现复杂度较高,而结构化方法虽然比较容易实现但在纠错性能上存在一定的损失,而且结构化方法对校验矩阵的结构也有苛刻要求,只有按照特定方法构造的码才能适用,比较常用的方法有Thomas J.Richardson等人基于近似下三角矩阵设计的编码方法[11],Lei Chen等人基于有限几何域构造的准循环LDPC码[12],以及一些改进的算法,如模循环算法[13]等。


(1)
编码的过程就是通过解上面方程得到校验位p的过程。但通常情况下矩阵求逆的运算过程非常复杂,直接进行处理会呈指数地增加硬件开销以及系统时延。但是,如果矩阵A可分解为A=L×U(L为下三角矩阵,U为上三角矩阵),那么就可以避免复杂的求逆过程,当引入中间变量v时,由方程可导出如下方程:
L×v=B×sT,
(2)
U×pT=v。
(3)
因为L和U都是三角结构的矩阵,所以可以通过迭代法,式(2)采用前向迭代、式(3)采用后向迭代就能够快速得到方程的解,从而可以避免效率非常低的矩阵求逆运算。
另外,注意到Radford M.Neal提出的编码方法中采用行重-列重乘积pi,j=(wr[i]-1)×(wc[j]-1)最小化作为优化手段,其中wr[i]和wc[j]分别表示矩阵中元素“1”所对应的第i行行重和第j列列重,这种手段存在一定的缺陷,当wr[i1]=wr[i2]=1(i1 2.1 设计思路 一般情况下,在LDPC码的校验矩阵H不满足系统码条件时,可以通过行列置换而获得满足系统码条件的校验矩阵。如果置换矩阵为E,那么就有H×ET=[A,B],[A,B]是满足系统码条件的校验矩阵。进而对A进行LU分解,可得到PAQ=LU,P和Q是和E具有相同结构的行置换矩阵和列置换矩阵。对校验矩阵H进行初等行列交换,为了满足校验关系,码字也只是对应交换映射位置,码字间的关系并不改变,即最小码距不变,因此不影响纠错性能。同时,如果v属于该码字空间,必然满足vHT=0,反之亦然。那么,要使vHT=0成立,一个[n,k]码字的校验矩阵H必然存在(n-k)个线性无关行,从而至少存在一种(n-k)×(n-k)的非奇异组合[14]。要降低LU分解后编码实现的复杂度,就要使分解后的得到的三角矩阵尽可能稀疏,最为关键的是得到这个恰当的(n-k)×(n-k)非奇异方阵,这一目的可以通过对校验矩阵H进行高斯消元来达到。 对于n阶非奇异矩阵进行LU分解的第k步操作是[15]: (4) 式中,k=1,2,…,n-1;i,j=k+1,k+2,…,n。 在二元域GF(2)上,主元必然选择“1”,式(4)中的乘、除法运算等价于与运算,而加、减法运算等价于异或运算;另外,为了减小存储空间、降低计算的复杂度,主元的选择将决定LU分解后矩阵的稀疏程度,为了避免Neal提出的算法中主元选择不恰当的情况,本文在综合考虑存储空间和计算复杂度的情况下采用最小行重中最小列重法,即先寻找最小行重的为主行,再从主行中寻找最小列重的为主元。 2.2 算法描述 根据上述设计思路,对校验矩阵H进行调整和LU分解。而LU分解本质上就是高斯消元,其中的U就相当于矩阵高斯消元的结果。使用最小行重中最小列重法作为LU分解中主元选择的策略,对校验矩阵进行高斯消元,并将过程中的行列置换操作,作为对校验矩阵H进行调整分割的依据。算法描述如下: ① 对校验矩阵H进行调整,得到(n-k)阶非奇异矩阵A; ② 初始化L=I(n-k)×(n-k),U=A; ③ 初始化向量r=1∶n-k和c=1∶n-k,用于存储行、列交换操作; ④ 初始化循环变量i=1; ⑤ 在U的剩余矩阵中统计i~(n-k)行每行的行重,找到最小的并与i行交换,同时更新向量r; ⑥ 交换L中的对应行; ⑦ 在U的剩余矩阵中统计i行元素为“1”的列的列重,找到最小的并与i列交换,同时更新向量c; ⑧ 进行高斯消元,消去U中第(i+1)~(n-k)行第i列的元素“1”,矩阵L也进行相应的消元变换; ⑨ 变量i不等于(n-k),则执行i=i+1,并跳至步骤⑤进行循环操作,否则循环结束。 根据以上所描述的算法,可以直接得到分解后的L、U矩阵,也能够通过r和c构造出行列置换矩阵。 根据本文提出的改进算法,按RadfordM.Neal发布的方法构造了一个512×1 024的校验矩阵,并分别采用原始方法和本文提出的改进方法进行LU分解,2种方法分解所得到的L矩阵和U矩阵中元素“1”的散点图如图2和图3所示,统计结果如下: 原始方法LU分解情况: (L)2122 + (U)1669=3791。 优化方法LU分解情况: (L)1905 + (U)1416=3321。 相比于方法分解得到的矩阵,优化后方法分解的结果元素“1”的数量减少了约13%,这表明了优化方法得到的矩阵具有更好的稀疏性,这也就能够进一步降低编码实现的复杂度,可见起到了优化的作用。 (a) L矩阵中元素“1”分布 (b) U矩阵中元素“1”分布 (a) L矩阵中元素“1”分布 (b) U矩阵中元素“1”分布 本文基于Neal的理论,针对LDPC码的特性,设计了一种基于LU分解的编码算法,改进了校验矩阵优化准则,保证了分解后的矩阵具有更好的稀疏性,进一步降低了编码实现的复杂度,具有较好的应用前景。这一算法的优势是:不限制校验矩阵的构造条件,具有较强的通用性;存储需求小,实现的复杂度较低,编码速率比较快。但是,因这一算法的通用性,使其对准循环结构等具有特殊结构的校验矩阵的编码并无贡献,因而也无法有效利用。 [1] GALLAGERR G.Low Density Parity-check Codes[M].Cambridge:MIT Press,1963:4-44. [2] GALLAGERR G.Low Density Parity-check Codes[J].IRE Trans. Inf. Theory,1962,8(1):21-28. [3] 马克祥,刘 毅,胡建华,等.LDPC码的一种低复杂度译码算法及关键电路设计[J].西安电子科技大学学报,2013,40(6):6-12. [4] CHUNGS Y,FORNEY G D,RICHARDSON T J,et al.On the Design of Low Density Parity Check Codes within 0.0045 dB of the Shannon Limit[J].IEEE Communications Letters,2001,5(2):58-60. [5] MACKAYD J C,NEAL R M.Near Shannon Limit Performance of Low-Density Parity Check Codes[J].Electronics Letters.,1996,32(8):1 645-1 646. [6] LI J P,MA J,HE G H.A Memory Efficient Parallel Layered QC-LDPC Decoder for CMMB Systems[J].Integration,the VLSI Journal,2013,46(4):359-368. [7] 王 飞,罗 益,王振华,等.LDPC码在BPSK通信系统中的性能分析[J].无线电通信技术,2015,41(1):13-16. [8] 马玉华,仰枫帆.采用空间分集的LDPC编码协作系统性能研究[J].无线电通信技术,2013,39(1):43-46. [9] MACKAY D J C.Good Error Correcting Codes Based on Very Sparse Matrices[J].IEEE Trans.Inf.Theory,1999,45(2):399-431. [10] TANNER R M.A Recursive Approach to Low Complexity Codes[J].Information Theory IEEE Transactions on,1981,27(5):533-547. [11] RICHARDSON T J,SHOKROLLAHI M A,URBANKE R L.Design of Capacity Approaching Irregular Low-Density Parity-check Codes[J].IEEE Transactions on Information Theory,2001,47(2):619-637. [12] CHEN L,XU J,DJURDJEVIC I,et al.Near Shannon-Limit Quasi-Cyclic Low-Density Parity-check Codes[J].IEEE Transactions on Communications,2004,52(7):1 038-1 042. [13] 王 健,刘绍华,杨仕平.一种新的LDPC码编码方法[J].无线电工程,2014,44(4):14-16. [14] 王新梅,肖国镇.纠错码——原理与方法.[M].西安:西安电子科技大学出版社,2001:52-59. [15] 杨绍祺,谈根林.稀疏矩阵——算法及其程序实现[M].北京:高等教育出版社,1985:42-48. 高宏伟 男,(1978—),硕士,工程师。主要研究方向:通信与信息工程。 Research on Modified LDPC Encoding Algorithm Based on LU Decomposition GAO Hong-wei (Unit91604,PLA,LongkouShandong265700,China) In order to make the check matrixHof Low Density Parity-check Codes (LDPC) meet the form of systematic code, reduce the complexity of LDPC and the storage space during coding, this paper proposes improved optimal criteria, and designs an algorithm based on LU decomposition. This algorithm uses complete pivot strategy to perform Gaussian elimination and row and column exchange to make theHhave the form of systematic code. The decomposed matrix has better sparsity to further simplify code design and reduce storage space and computation complexity. The simulation results show that the modified algorithm is independent of the constitution of check matrix and favourable to hardware implementation, and has no influence on performance, so it has better application prospect. check matrix;systematic code;LU decomposition;LDPC;encoding;modified algorithm 10.3969/j.issn.1003-3106.2017.04.08 高宏伟.基于LU分解的LDPC编码改进算法研究[J].无线电工程,2017,47(4):31-34. 2017-01-12 TN911 A 1003-3106(2017)04-0031-042 改进的编码方法
3 仿真验证结果


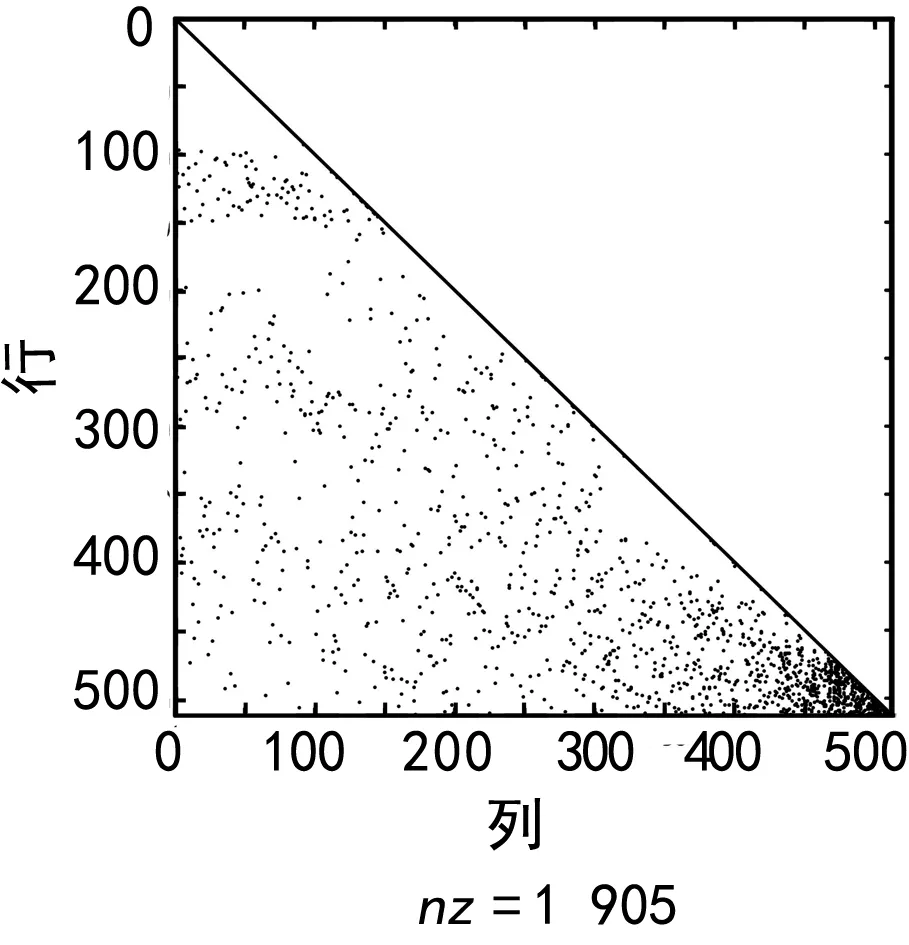
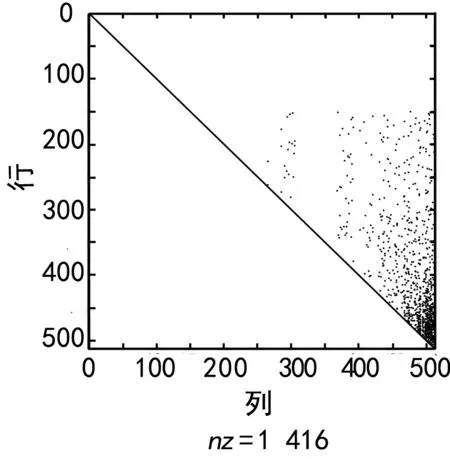
4 结束语
