我国上市银行系统关联性研究——基于方差分解的网络拓扑分析

■文风，汪洋

我国上市银行系统关联性研究
——基于方差分解的网络拓扑分析

■文风，汪洋

2008年金融危机以后，系统性风险成为理论界与监管当局的重点研究领域。本文使用2013年11月至2016年9月间我国16家上市银行股价日波动率数据，通过广义方差分解模型（GVD）得到我国上市银行系统关联性矩阵，进而得到描述系统及机构间关联性的网络拓扑图。研究发现，我国上市银行系统具有“小世界”和“无标度”的网络特性，并且在样本期间内，上市银行的机构关联性呈现上升趋势，2015年股灾之后，我国银行机构的系统性风险在短期之内不但没有得以消化，反而累积了更多的风险。因而，监管部门在现今阶段不能放松警惕，而应该加强对系统重要性机构的监管。

关联性；广义方差分解；银行；监管部门

文风，华中科技大学经济学院，研究方向为金融机构与金融市场；汪洋，华中科技大学经济学院，研究方向为时间序列与金融经济学。（湖北武汉430074）

一、引言

2008年金融危机以后，理论界和监管当局深刻反思金融系统性风险。金融稳定委员会（FSB）将系统性风险定义为针对金融机构而言、由金融系统局部破坏或者全面受损引起的，并且可能对实体经济造成严重负面影响的风险。该定义强调了系统性风险的外部性概念，任何类型的金融机构和金融市场都有可能在一定程度上受到其他金融机构尤其是系统重要性金融机构的负外部性影响。外部性理论认为，金融机构通常只会着眼于自身业务的风险和收益，而不会在意整个金融体系的风险，当市场出现重大的不利因素后，有可能会导致所有金融机构同时采取行动（比如金融危机期间各机构疯狂抛售手中持有的证券的行为），引起系统性崩溃。

金融机构作为金融系统的重要主体和金融风险的主要载体，研究它们之间的关联性是理解金融系统性风险的核心。“关联性”是资产配置、衍生品定价以及风险管理等众多金融研究领域里的重要议题，对关联性的计量是测度市场风险、信用风险、交易对手方风险以及系统风险的重要组成部分。描述关联性的传统方法是使用简单的统计学测度两者之间的皮尔逊相关系数，然而有学者认为，使用皮尔逊相关系数只有助于描述研究对象的线性相关程度，而在测度非线性相关程度时皮尔逊系数则表现得过于苛刻。此外，在对变量进行非线性单调转换时，线性相关系数也有可能发生变化，比如两个市场收益率是线性无关，而波动率却有可能线性相关。考虑到线性相关系数在描述金融市场关联性所具有的固有缺陷，学者们提供了诸多改进思路。第一是在原有的普通相关系数法的基础上发展出拟相关系数法测量金融数据的联系性，比如Engle&Kelly（2011）通过计算所有变量成对的平均相关系数来描述相关程度；其次是构建新的测量相关程度的模型，比如Krishna H.K et al（2015）利用由Sklar和Nelson等人发展的Copula函数描述金融时间序列之间的相关性。运用Copula理论分析金融市场尾部相关性具有得天独厚的优势，不同Copula函数形式可以用来分析不同极端市场条件下的相关性，金融危机以后，Copula方法在风险管理和资产配置等方面的研究领域中备受青睐（Riadh Aloui et al，2016）。尽管以上理论的发展在测度金融市场的相关性方面做出了重要贡献，但也存在着种种不足。首先，无论是拟相关系数方法还是Copula方法一般只适用于局部的关联性分析，而不能很好地描述系统关联性；其次，我们在研究金融系统性风险时，往往会关注影响力巨大的系统重要性金融机构，而这两种方法均不能做到对金融网络结构特征的识别。为解决这些传统方法力不能及的问题，近年来，许多经济金融学家尝试利用物理系统和社交系统等领域已经发展成熟的网络理论模型，去解释金融危机过程中的风险外溢等现象（巴曙松等，2013）。网络分析方法在经济金融的应用范围较广，比如在金融市场方面有关于国内国际的股票市场联动性方面的研究（李岸等，2016），在宏观经济方面有关于区域宏观经济增长空间关联性的研究等等（李敬等，2014）。从大多数文献来看，网络理论的发展为研究金融市场关联性以及金融危机的阐述提供了新的思路，既打破了传统重视局部关联性研究的思维盲区，以整个金融系统为视角评估金融市场的风险相关性，又能借助于网络模型以可视化的形式识别出金融机构之间的关联性以及系统重要性金融机构。而且运用网络模型可以监测系统重要性金融机构的风险溢出效应，并据此分析金融危机时期金融机构的风险传染机制（Diebold& Kamil，2011）。

近年来，我国金融业呈现出准混业化经营的趋势，面临互联网金融的剧烈冲击以及为满足自身业务发展的需求下，银行、基金、证券、保险等业务的边界逐渐模糊，传统“一行三会”分业监管模式遭遇到巨大挑战。在此形势下，利用网络模型研究我国金融机构的关联性成为一个重要议题。欧阳红兵等（2015）通过网络模型研究13家上市银行机构的股价波动率，认为整个体系的关联程度较高，说明我国金融机构可能存在过度关联的现象。其中国有银行之间的风险溢出效应更大，传统四大行则处于系统内的核心位置，应该受到监管当局的重点关注。吴念鲁等（2015）通过网络模型计算我国金融机构之间的聚集程度，认为我国银行同业间聚集系数在金融危机之后逐年上升，并且也认为四大行处于系统重要性金融机构的地位，监管机构应该加强对这些机构的管理水平。邓向荣等（2016）认为在金融混业经营的背景下，金融风险传染网络具有多层次、多通道、交互式的特点，传统的分业监管模式将逐渐不能满足新的金融业态，因此，具有系统重要性意义的、在金融网络中信息传染的关键节点的金融机构理应纳入宏观审慎监管的范畴。

国内现有文献利用网络分析法研究金融机构系统性风险还处于起步阶段，所使用的研究方法较为简单。本文采用16家上市银行的股价日波动率数据，通过向量自回归模型（VAR）以及广义预测误差方差分解（GVD）模型构建出有向权重关联性矩阵，并基于关联性矩阵提供可视化的金融机构关联性网络拓扑图，分析近年来我国上市金融机构的风险关联性以及系统性风险的测度。

本文第二部分为理论与方法介绍，第三部分为实证分析，最后一部分为结论及政策建议。

二、理论与方法

（一）网络系统关联性测度

网络模式是当前经济社会最常见的一种存在方式，用网络理论分析和解决现实问题已经成为经济学和社会学领域的重要研究方向。假设网络N由N个节点以及L条连接节点的连线组成，我们用Sij表示节点i和节点j之间的距离，它定义为从节点i到节点j所经历的最少连线的数目。这就意味着对于任意的i和j，只要存在Sij≤N-1，那么网络N则是相连的。比如由0和1两种元素可以组成的邻接矩阵可以构造出最简单的网络结构，假设矩阵A是由N×N维的邻接矩阵，当节点i和节点j之间相连时，Aij=1，否则Aij=0，由于Aij=Aji，此时矩阵A一定是对称矩阵。邻接矩阵A作为网络模型的代数表达形式，网络的所有性质都被赋予在邻接矩阵A中，因而对于网络关联性的研究可以转化为对邻接矩阵A的关联性研究。

测度邻接矩阵关联程度的主要指标有“度”和“直径”。网络节点的“度”是指这个节点与其他节点连线的数量，因此容易推算出节点的度服从0、1、…、（N-1）的离散单变量分布。网络的特性与“度”的分布有着紧密的联系，包括其分布的尾厚、偏度、规模和位置，通常分布的位置用均值来测度，并且可以作为衡量网络整体关联性的基准统计量，如果“度”的均值越大，则说明网络的关联性越强。度的概念强调直接关联，然而在网络中也存在间接关联，即节点i与节点m相连，而节点m又与节点j相连，因此可以认为节点i与节点j间接相连，当网络中任意两个节点间接相连所需要经过的节点越少，说明这个网络的关联性越强。由于间接相连的最小连线数目就是前文所描述的距离Sij，因此可以记网络的直径为Smax=maxi，jSij。直径可以作为衡量网络关联程度的另一个基准指标，网络的直径越小，系统的关联性越强。

（二）系统关联性表

假设维带有正交冲击的协方差平稳数据的生成过程为xt=Φ（L）ut，其中Φ（L）代表滞后系数矩阵，Φ（L）=Φ0+Φ1L+Φ2L2+…，E（utu′t）=I。在此一般性数据生成表达式中，容易推算出变量之间的所有关联性都包含在系数矩阵Φ中，其中即期的关联性主要体现在系数Φ0中，而动态的关联性主要体现在{Φ1，Φ2…}。然而在很多情况下测量其关联性可能需要涉及过多的系数，因此通常需要将系数矩阵Φ转换成一个更为精简的形式，来更好地反映系统的关联性。

一种常见的转换方式是通过方差分解方法将原本复杂的系数矩阵转化为可以反映系统关联性的矩阵，并据此衍生出整个网络分析法的基石——关联性表。关联性表的基本结构如表1。关联性表基本元素是由方差分解的结果构成，标记左上方的矩阵为方差分解矩阵，为D=[dHij]。矩阵D的非对角元素即为N步预测误差方差分解的结果，每一个元素衡量成对变量的有向关联性。记从节点j到节点i的关联性为CHi←j=dHij，反映的是节点j到节点i的“出度”。并且在通常情况下，节点j到节点i的“出度”与节点i到节点j的“出度”并不相同，即CHi←j≠CHj←i，因此方差分接矩阵D中共N2-N个非对角元素恰好衡量N个网络节点的成对有向关联性。此外，我们定义节点j与节点i的“净”的关联性为CHij=CHj←i-CHi←j，“净”值反映出节点对节点j的“净出度”。

网络关联性表最右边一列是对应行的非对角线元素之和，表示其他节点对该节点的冲击所产生的H步预测误差方差的百分比，记其他节点对节点i的总的有向关联性为C，即节点i的“入度”。同样的，网络关联性表最下一行是对应列的非对角元素之和，表示该节点对其他节点的冲击，记节点j对其他节点的总的有向关联性为CH·←j=，即节点j的“出度”。与成对节点关联性的测度一样，我们定义节点i与其他所有节点总的净关联性为

在网络N中共有N个总的净关联性测度值。而系统总的关联度即可定义为CH=

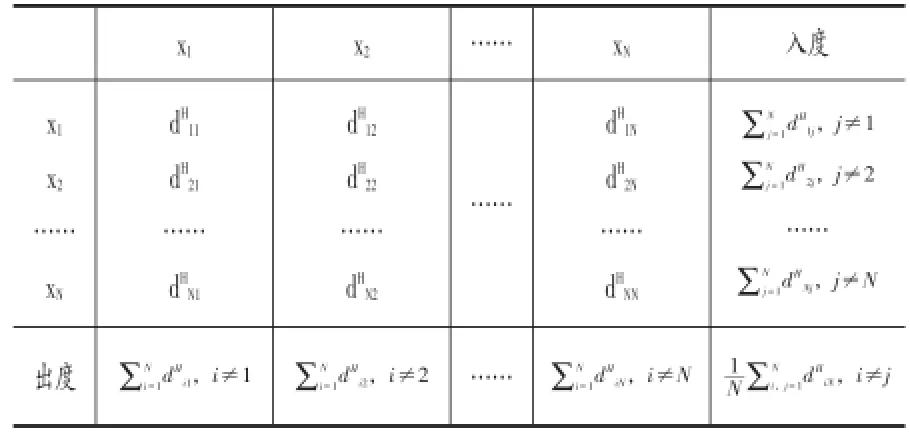
表1 网络关联性表

（三）基于GVD模型的方差分解

方差分解方法是指将系统内任一变量的预测均方误差分解成系统中各变量的随机冲击所做的贡献，进而计算出各变量冲击的贡献占总贡献的比率。通过方差分解可以揭示变量相对重要性信息的时变情况，即通过方差分解方法可以观察到一个变量的运动轨迹有多大程度由自身冲击决定，有多大程度由其他变量的冲击决定。在正交的数据生成系统中，由于权重和的方差近似等于方差加权之和，因此方差分解比较容易计算。而在实际应用中，冲击通常并不具有正交性，从而给经济学研究带来一定程度的困扰。由Sims（1980）提出的VAR模型中，通过使用乔里斯基因子方法可以将冲击项正交化，可以有效地解决正交性问题。同样的，由VAR模型衍生出来的SVAR模型以及广义方差分解模型（GVD）、动态随机一般均衡模型（DSGE）等均可以得到正交化的方差分解矩阵。值得一提的是，VAR模型或者SVAR模型在进行乔里斯基分解的过程中对变量的排序极为敏感，而在本文研究中由于研究的对象较多，又不可避免涉及到排序问题，因此传统的VAR模型或者SVAR模型可能不适用于本文的通过方差分解估计相关性矩阵的步骤。而GVD模型独立于变量的排序，更适用于作为本文的方差分解矩阵的估计方法。

给定t时刻的信息集和变量i的各期冲击Ui，t+1，Ui，t+2，…，Ui，t+h，可以得到随机过程Zt+h的条件预测方差为：

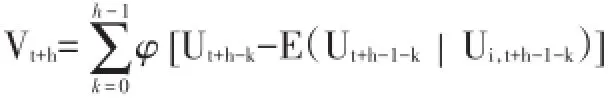
其中{Ut}～N（0，∑），E（Ut｜Uit=δi）=（σ1i，σ2i，…，表示一个标准差的冲击。容易推算出E（Ut+h-1-k｜Ui，t+h-1-k）=（σ-1ii∑ei）Ui，t+h-1-k，其中k=1，2，…，h-1；i=1，2，…，m；ei是第i个元素为1，其他元素为0的m维列向量。从而可以进一步求出条件预测误差方差为：

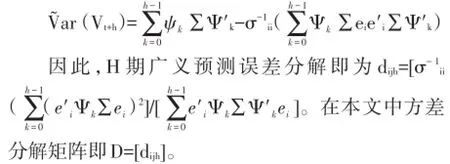
三、实证检验

（一）数据与样本

商业银行作为间接融资的主体，其抵抗风险的能力对我国金融市场的稳定性有着至关重要的作用。本文的研究主体为包括中、农、工、建四大行在内的16家上市银行，这些银行由于资产规模庞大、业务种类繁杂，可以作为我国商业银行的代表。此外，上市银行披露的财务数据和市场行情数据又相对丰富，为本文的研究提供一定的可行性。

商业银行之间的关联性研究通常会涉及到对银行间业务分析，然而商业银行之间以直接或间接的方式进行对手方交易或者资产头寸互相持有，这使得仅仅依靠在资本市场上所披露的财务报表获取高频的业务数据并进行进一步分析变得不大可能。根据有效市场理论，股票市场可以反映出所有历史记录的信息，这为学者们利用股票市场数据研究金融市场或者金融机构的关联性提供了理论基础。因此，本文尝试利用股票市场的数据研究金融系统的风险关联性并揭示我国金融机构的系统性风险。在金融学中，波动率往往是衡量风险的理想指标，因此本文选取从2013年11月至2016年9月之间16家上市银行共796个交易日的日波动率数据作为衡量金融机构风险的代理指标。由于日波动率的估计方式较多，一般认为由ARCH族模型估计出来的日波动率最为精确，因此本文采用的日波动率均由GARCH模型估计所得，数据来源为锐思数据库。

图1描绘了16家上市银行日波动率走势。总体来看，16家上市银行日波动率走势具有高度的一致性，这说明我国上市银行之间的关联性可能较强。近三年来上市银行股波动率走势大致可以分为三个阶段，第一阶段为2013年第四季度至2014年第四季度，在此期间，我国银行业稳步扩大资产负债规模、完善公司治理、健全组织体系、逐步提升经营管理效率和风险防控水平。总体来看，我国上市银行在此阶段经营态势良好，资本充足水平维持在高位，市场对我国银行业信心较强，银行股风险较低；第二阶段为2014年末到2016年第一季度，该区间内国际国内金融市场以及大宗商品价格均出现了剧烈的波动，2015年我国证券市场经历了一轮暴涨暴跌的周期加剧了整个金融体系的不确定性。同时，在经济下行的压力下，我国金融业资产质量下行压力也较大，国际市场风险、房地产风险、政府债务风险与经济增长率骤降等风险均对我国金融体系的发展造成潜在威胁。第三阶段为2016年第二季度之后，随着大盘趋于稳定，银行股的波动率也下降到2014年的水平。

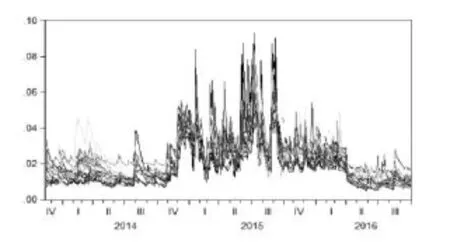
图1 上市银行股价日波动率

（二）系统关联性表的构建

本部分以第三阶段样本数据为例详细介绍网络模型的构建。首先，股价日波动率序列具有明显的序列相关性，在建立向量自回归模型之前我们首先将原始数据进行对数处理，既有利于得到相对平稳的数据，又能够得到一个具有近似正态分布的时间序列，以满足方差分解步骤对正态性数据的要求。我们使用eviews软件对经过处理的数据进行平稳性检验，检验结果认为所有序列均在10%的水平下拒绝单位根检验。继而进行VAR建模的滞后期选择检验，检验结果显示滞后1阶建模最佳。因此，我们构建VAR(1)模型，并进而得到所有银行广义方差分解的结果。根据其他学者的研究经验，取向前广义预测误差方差分解的步数为H=10，得到的方差分解关联矩阵D。根据表1中出度和入度的算法，我们得到第三阶段的系统关联性表（表2）。

表2 系统性关联矩阵

我们首先观察表2中的方差分解矩阵部分，该矩阵为16×16的方阵。其中对角元素表示金融机构对自身的关联性，因而不难理解对角线上的元素值通常较大；非对角元素表示成对金融机构的关联性，正如第二部分所述，由于dHij表示节点j到节点i的关联性，dHji表示节点i到节点j的关联性，所以该方阵并不具有对称性。比如该方阵中非对角元素数值最大为21.96，表示华夏银行对工商银行的关联性，而其对称元素仅有1.42。这说明当华夏银行的波动率受到冲击时，工商银行的波动率很大程度上也会受到影响。换句话说，华夏银行的风险可能会传导到工商银行。而工商银行的波动率受到冲击后对华夏银行的影响不大，工商银行的风险不能有效地传导到华夏银行。

系统关联性表的最后一列元素表示对应机构的关联性入度，即其他金融机构对该机构的关联性，入度值越大表示在金融市场的波动中该机构更加脆弱。入度值最大的是工商银行，可见银行系统的脆弱程度与资产规模不尽相关。此外，宁波银行、光大银行、中国银行的入度也处在高位。对于脆弱程度较高的银行，应该加强资产质量的管理，提升中间业务收入，提高自身抵御风险的能力。

表2的倒数第二行元素表示对应机构的出度，也就是该机构对其他金融机构的影响能力。出度值越大，表明该机构越有可能成为系统重要性机构。华夏银行的出度值居于首位，从表3中可以看出华夏银行对大多数上市银行的关联性都较高，因此是系统重要性银行。2016年上半年，华夏银行资产质量下行压力较大，关注类贷款余额节节攀升，这可能预示着未来华夏银行不良率可能上升，造成金融市场对华夏银行资产质量的担忧，反映在股市中则表现为股价波动率的协同上升。此外，华夏银行还面临着第一大股东德银股权减持的威胁，加大了市场对其未来经营的不确定性。紧接着是兴业银行、广大银行、中国银行，这些银行的出度都在100以上，表明这些机构对我国金融市场的影响能力较大，应该成为我国监管当局重点监控的对象。

表2最后一行元素显示各机构关联性的净值，当元素数值为正时，表示对应机构对整个系统有风险传染性；当元素数值为负时，表示对应机构受到系统的风险传染。结果显示，华夏银行、兴业银行等作为系统重要性机构，对整个系统有着举足轻重的影响；而工商银行、民生银行等机构应该加强自身风险管理，提升自身的风险抵御能力。系统总的关联程度为79.86，处于较高的水平，这与我们研究的行业有关，金融行业不但容易受到行业层面的冲击，也容易受到宏观经济层面和政策层面的冲击，因此上市银行股价波动率的关联程度处于高位也较为符合我国经济金融发展的实际情况。

（三）系统性风险可视化分析

利用网络模型构建拓扑分析图能够将系统性风险直观形象的表现出来，本部分我们将基于网络拓扑分析图比较样本期间内三个阶段的系统系风险。网络拓扑图是基于方差分解矩阵绘制而得，我们将展示出样本期间内关联性最强的有向连线。由于每个时期将会有120条表示净关联性连线，三个时期共有360条连线。按照经验，我们将绘制关联性排在前15%的有向连线。绘制工具为UNINET软件，拓扑图见图2、图3和图4。

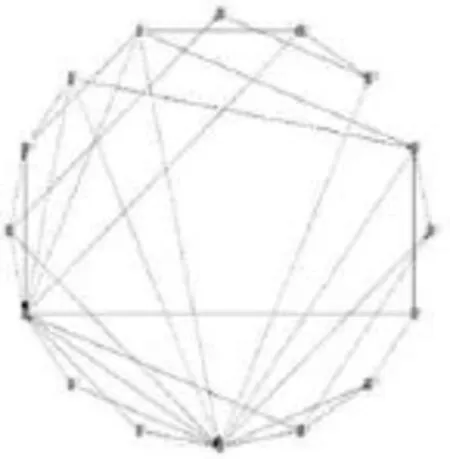
图2 第一阶段网络拓扑图

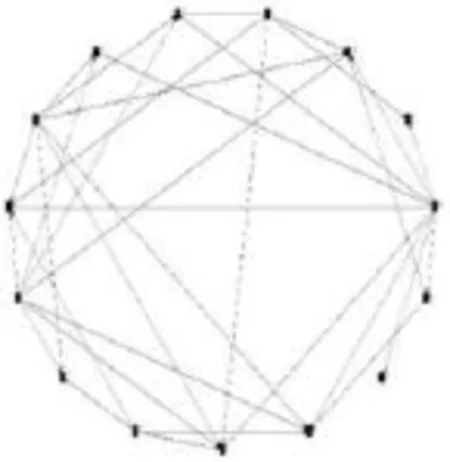
图3 第二阶段网络拓扑图

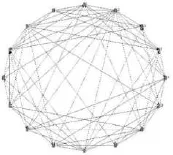
图4第三阶段网络拓扑图

图2 至图4分别表示样本期间三个阶段的关联网络图，显示出我国上市银行信息溢出的关联网络具有复杂网络的结构特征。经测算，三个阶段衡量网络拓扑图关联程度的“度”的均值分别为14.17、16.19以及30.00，对应的“直径”则分别为1.04、1.00、0.81，“直径”的数值偏小反映出金融市场联系紧密，金融网络模型具有“小世界现象（Small-World Phenomena）”的特性。金融市场网络模型还具有“无标度现象（Scale-Free Phenomena）”的特性，即大部分节点只与很少的节点有关联，但也有极少数节点与其他较多的节点有关联。“无标度”特性造成金融体系受到金融机构系统性风险传染的概率并不大，而一旦系统重要性机构受到风险传染，则整个网络的脆弱性将会集中体现出来。通过比较三个阶段的网络拓扑图，我国16家上市银行信息溢出效应愈发强烈。与第一阶段相比，第二阶段正处于我国股市经历大幅变动的时期，上市银行共同的风险敞口迅速放大，信息传染能力显著增强，造成金融机构之间的关联性出现上升趋势。在经历“过山车”的暴涨暴跌之后，市场投资者在第三阶段的风险厌恶情绪明显上升。伴随着宏观经济基本面的持续下行与银行资产质量不断恶化，金融市场参与者对市场的信心急剧下降以及对未来股市收益率的不确定性迅速上升，导致单支银行股票价格下跌可能会引起其他上市银行股票的联动下跌。基于网络拓扑图可以直观的发现，第三阶段上市银行的系统关联程度大大上升，这意味着外生的冲击将以更多的渠道对系统内其他机构产生影响。一旦在某个时刻受到一定程度的外生冲击，系统关联性越高就越容易放大系统冲击的破坏能力和影响范围。我国银行类风险在第三阶段期间不仅没有将股灾期间的风险释放出去，反而积累了更多的风险。

网络拓扑图连线表示成对机构之间的净关联性，因而利用网络拓扑图有助于我们直观地寻找出系统重要性机构或者系统脆弱性机构。不同金融机构在不同阶段的系统重要性是有所变化的。在第一阶段，北京银行和工商银行很容易受到其他银行的风险传染，而在第二阶段，系统脆弱性银行则是北京银行、南京银行和农业银行，在第三阶段，系统脆弱性银行包括宁波银行、平安银行、浦发银行以及民生银行。可以发现，资产规模较小的银行更加容易受到系统性风险的传染，比如北京银行、宁波银行以及南京银行作为区域性银行，资产规模以及业务范围都比不上其他上市银行，在各个阶段都受到其他银行风险传染的可能性更大。在三个阶段中，系统重要性银行包括华夏银行、建设银行以及交通银行等。无论是对于系统重要性机构，还是系统脆弱性机构，监管当局和机构自身都应该加强监管与风险控制，确保这些机构不会成为危机爆发的导火索。

四、结论及政策建议

2008年全球金融危机以后，金融系统性风险逐渐成为学界和监管当局的研究热点。针对以往学者在研究系统性风险问题时往往存在变量与数据选取不恰当、方法与模型具有局限性以及分析结果不直观不全面等种种不足，本文基于2013年11月至2016年9月16家上市银行日波动率数据，通过广义误差方差分解模型（GVD）得到的系统关联性矩阵，并以此构建网络模型，绘制相应的网络结构拓扑图，分析我国上市银行的关联特征，揭示我国上市银行系统性风险的时变特征。

研究表明，我国上市银行在样本期间内的信息溢出网络具有“小世界”和“无标度”的特性。也就是说，从系统来看，我国金融体系具有较强的系统关联性；从单个机构来看，尽管大部分金融机构只与少数其他金融机构关联性较强，然而一旦系统重要性机构受到外生冲击，将会对整个金融体系造成强烈的冲击。通过比较三个阶段的网络拓扑图结构，我国上市银行在股灾期间的系统关联性比第一阶段有所加强，这意味着股灾期间我国上市银行体系的风险有所上升。而在股灾之后的第三阶段，我国上市银行的系统关联性并没有随之减弱，这有可能意味着股灾之后我国上市银行的风险在短时间内不但没有消化掉，反而积累了更多的风险。宏观经济下行压力加大、房地产市场的不确定性加强、货币政策的不确定性等等不利影响都会造成投资者对我国金融业前景产生悲观态度，反映在股价中则是一只金融股价格下跌会导致整个金融股价格下跌的“羊群效应”现象。因此在当前阶段下，为防止金融机构出现系统性的破坏，如何加强对系统重要性机构的识别、金融业务监管和金融风险监控成为监管当局的重要课题。

在使用网络拓扑模型识别系统重要性机构时发现，我国上市银行的系统重要性是随时间发生变化的。总的来看，系统重要性机构包括华夏银行、建设银行以及交通银行等，系统脆弱性银行包括宁波银行、南京银行、北京银行等。金融机构的系统重要性在一定程度上与其资产规模有关，比如建设银行作为我国银行业资产规模最大的银行，其股价波动将会对其他银行产生传染性影响，而宁波银行、北京银行、南京银行等作为地区性银行，较容易受到其他金融机构的风险传染。此外，金融机构的系统重要性还取决于银行间对手方交易、金融机构对市场辐射能力、政策等因素，然而对于这些因素，变量的选取和数据的收集都极为困难，为我们进一步地分析带来障碍。换而言之，网络拓扑模型的优点就是能抛开机构对手业务等数据的收集，直接从股价入手分析金融机构的关联性，并识别出系统重要性机构，以此为监管当局政策制定提供一定的参考价值。

[1]李政，梁琪，涂晓枫.我国上市金融机构关联性研究——基于网络分析法[J].金融研究,2016， (08):95～110.

[2]巴曙松，左伟，朱元倩.金融网络及传染对金融稳定的影响[J].财经问题研究,2013，（02）:3～11.

[3]李岸，粟亚亚，乔海曙.中国股票市场国际联动性研究——基于网络分析方法[J].数量经济技术经济研究，2016，（08）：113～127.

[4]邓向荣，曹红.系统性风险、网络传染与金融机构系统重要性评估[J].中央财经大学学报，2016（03）：52～60.

[5]吴念鲁，徐丽丽.我国银行同业间网络的拓扑结构特征分析及启示[J].当代财经，2015，（11）：42～52.

[6]欧阳红兵，汪清梅.基于网络拓扑的中国银行体系关联度分析[J].武汉金融，2016，（01）：14～17.

[7]Diebold,F.X，and K.Yilmaz.(2014).On the NetworkTopologyofVarianceDecompositions: Measuring the Connectedness of Financial Firms. Journal of Econometrics,182，（1）：119～134．

[8]Pesaran，H.M，andY.Shin.(1998). Generalizedimpulseresponseanalysisinlinear multivariate models.Economics Letters 58,17～29.

[9]Markku Lanne,and Henri Nyberg.（2016）. Generalized Forecast Error Variance Decomposition for Linear and Nonlinear Multivariate Models.Oxford Bulletin of Economics and Statistics,78(4):595～603.

[10]Engle,Robert F.and Kelly,Bryan T.（2011）. Dynamic Equicorrelation.NYU Working Paper No. FIN-08-038;Chicago Booth Research Paper No.12-07;Fama-Miller Working Paper.Available at SSRN: https://ssrn.com/abstract=1354525 or http://dx.doi.org/ 10.2139/ssrn.1354525

[11]Koirala KH,et al.(2015).Energy prices and agriculturalcommodityprices:Testingcorrelation using copulas method.ENERGY

[12]Aloui，R，&BenAïssa，M.S.（2016）. Relationship between oil,stock prices and exchange rates:A vine copula based GARCH method.North American Journal of Economics and Finance,http://dx. doi.org/10.1016/j.najef.2016.05.002

F830

A

1006-169X（2017）02-0064-07