高速射弹出水过程中水弹道问题研究
2017-03-28施红辉孙亚亚高聚瑞
侯 健,施红辉,孙亚亚,高聚瑞
(1.海军工程大学 兵器工程系,湖北 武汉 430033;2.浙江理工大学 机械与自动控制学院,浙江 杭州 310018; 3.杭州杭汽轮压缩机有限公司,浙江 杭州 310022)
高速射弹出水过程中水弹道问题研究
侯 健1,施红辉2,孙亚亚2,高聚瑞3
(1.海军工程大学 兵器工程系,湖北 武汉 430033;2.浙江理工大学 机械与自动控制学院,浙江 杭州 310018; 3.杭州杭汽轮压缩机有限公司,浙江 杭州 310022)
在研制高速射弹出水实验装置的基础上,利用实验和数值模拟的方法研究了细长圆柱型射弹(简称射弹)高速出水时包裹着射弹的超空泡的发展、脱落及其与自由面相互作用的全过程。根据测得的实验数据,计算出高速射弹出水过程中的空化数和阻力系数,参考Reichardt和Munzner以及Logvinovich公式,给出了阻力系数和空化数的多项式关系拟合公式,进一步形成了阻力系数归一化数值处理方法。结果表明:该高速射弹出水瞬间存在攻角时,非轴对称的空泡溃灭会使射弹的运动方向发生偏转;适当增大射弹的长径比或空化器长度,有利于高速射弹的水下运动减阻。基于FLUENT软件并采用VOF方法,对高速射弹出水过程进行了三维数值模拟,计算结果与实验结果吻合良好。该文还给出一个出水过程中水弹道偏转的示例,说明射弹在水下与超空泡壁面的碰撞滑移会引起水中弹道的偏移。
超空泡;水弹道;高速射弹;射弹出水;阻力系数;数值模拟
射弹在水下高速运动时其表面低压区的水会变为水蒸气,形成水蒸气混合的空泡,称为空化现象。航行体出水时,空泡内的压力升高,导致其中水蒸气会再次相变成水,形成溃灭。水下射弹超空泡出水问题是超空泡流动的一个重要分支,射弹的运动方向为垂直或是倾斜向上,主要应用在水下潜艇或者水下潜射导弹上[1]。由于水深变化和重力效应的存在,射弹出入水的过程属于非定常流动,国内外许多专家学者对此进行了深入研究。国外Waugh、Xing-Kaeding等对航行体带空泡出水过程中自由液面和空泡的溃灭及重力影响规律进行了实验研究[2-3]。Neaves等研究了航行体入水时超空泡与自由面的相互作用,对于二维情况下的流场、压力及航行体阻力进行了数值模拟[4];国内鲁传敬等人利用CFD方法以及动网格技术对细长体出水过程中射弹受力波动、液面的升高、射弹尾部拖水等问题进行了分析研究[5]。王一伟等对航行体有攻角出水全过程进行了数值模拟,得到航行体关键截面的全时程载荷响应,分析了航行体空泡形状和表面压力的演化特征,解释了航行体出水载荷的直接形成原因[6]。
此外,美国的明尼苏达大学和宾夕法尼亚州立大学在水洞中对超空泡流场进行精细测量,然后开展高精度计算机数值模拟[7-8]。然而应该注意的是,相似准则不是到处可以使用的,而且用水洞可模拟的流场也是有限的,例如弹道轨迹问题在水洞中是无法解决的,因此开展射弹模型试验研究是必须的。本文介绍笔者的研究团队近年来完成的出水弹道方面的一些研究结果,主要包括高速射弹阻力系数的拟合、对出水射弹进行三维流场的数值模拟以及弹道轨迹发生偏转的研究,并且通过实验与数值模拟结果进行对比,其结果吻合良好。
1 实验模型与工况
实验是在一台高速射弹出水实验装置上进行的[9-10],该装置可以将射弹加速到100 m/s以上。采用Photron公司的Fastcam Sa 5高速摄像机,最高拍摄速度可达一百万帧每秒。实验前水箱中的水是静止的,处于常温状态。实验所采用的射弹模型材料为铝镁合金,其外形及尺寸如图1所示,具体的几何参数见表1。
将拍摄到的细长圆柱体出水照片导入AutoCAD软件中,考虑到有机玻璃和水的折射问题造成的测量误差,在实验开始前将一把带有刻度的直尺放在射弹将要通过的位置,如图2所示,利用该刻度尺分别换算测量出空气中和水中相邻两幅时序照片中射弹的实际位移,为了减小测量误差,每次实验均测量3次以上并取平均值。表1给出了4种不同的实验工况,本次实验的拍摄频率均为5 000 s-1,由于拍摄频率已知,可计算出射弹在相邻两幅时序照片中的平均速度。表1中最后一列给出了空化数σ=0时的阻力系数Cd0的参考值;表中,p0,H,v0分别是气体驱动压力、水深和弹体初速度,m为质量,ψ为长径比。

图1 实验模型的尺寸参数

图2 高速摄像机拍摄的直尺照片
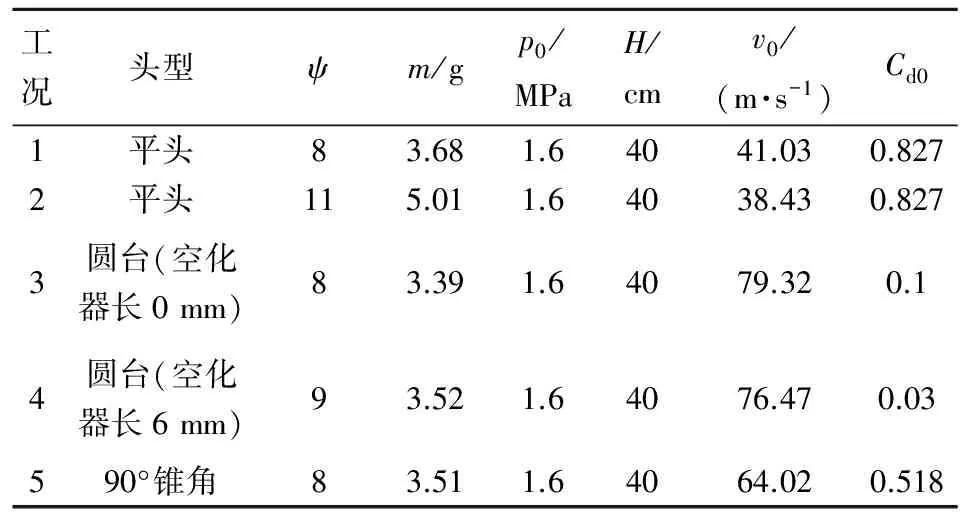
表1 不同工况下的实验参数汇总表
2 实验结果
图3是90°锥角的射弹在1.6 MPa(绝对压力)的驱动压力下出水过程的高速摄影照片(工况5),图中相邻两幅时序照片的时间间隔Δt=0.4 ms,每张照片的实际宽度为50 mm。图3中(1)~(8),射弹在水下自下而上地运动,射弹被椭球体的自然超空泡完全包裹,经研究分析可知,超空泡的形状满足Logvinovich的独立膨胀原理[11]。在图3(9)中,射弹开始伸出水面,并带出水冢[12]。射弹在图3(12)中已经离开水面,但是尾部拖出了一个水柱。然后射弹在空中飞行,而水柱的惯性使它发展成向上喷溅的水花(图3中(13)~(19))。超空泡从图3中(10)和(11)开始出现明显的溃灭,空泡的下半部分迅速变成空化尾迹(图3中(12)和(13));而空泡的上半部分在收缩变小的同时,与大气接通,并与水面上的水花形成了联动耦合流场[13]。注意到超空泡壁面上有射弹碰撞的痕迹,Savchenko[14]称之为滑移,这也可以用来解释射弹出水后弹道轨迹向逆时针方向偏转的原因。表1中其他4个工况的流场可视化照片,已在文献[9]中发表。

图3 工况5射弹出水过程高速摄影照片
取射弹模型出水瞬间为0 ms时刻,测得它们的速度v随时间的变化关系如图4所示。出水前射弹在水下运动时(即t<0 ms),它们的速度都在逐渐衰减,5个工况的变化趋势相似。在出水的瞬时,即分别在0.8 ms(工况1)、2.4 ms(工况2)、0.4 ms(工况3)时刻,射弹的速度较前一时刻有小幅度的增加,关于这个速度增加,笔者有水花喷溅射弹底部导致加速的解释[10],还有出水后弹丸甩负荷导致加速的解释[15]。另外,出水后弹丸的速度仍缓慢减小,这应该是水柱拖住弹丸尾部、空气阻力和弹丸重力共同造成的[16]。

图4 射弹模型速度随时间变化
图5给出了测得的空化数σ和阻力系数Cd的关系,Cd用文献[17]的公式算出。Reichardt和Munzner[18]以及Logvinovich[11]分别给出Cd和σ应满足的公式:
Cd=Cd0(1+σ+0.028σ2)
(1)
Cd=Cd0(1+σ)
(2)
式(1)和式(2)中Cd0是空化数σ=0时的阻力系数,对于圆盘空化器,Reichardt和Munzner给出Cd0=0.805,而Logvinovich取Cd0=0.827;对于工况3、工况4、工况5,柯乃普[19]给出Cd0分别为0.1,0.03,0.518。对实验值进行多项式拟合,公式如下:
(3)
(4)
公式后面的括号里给出了适用范围。获得的拟合函数曲线如图5所示,根据图5(a)和图5(b),在相同空化数下,工况1的阻力系数大于工况2的阻力系数,工况3的阻力系数大于工况4的阻力系数,再结合图4中射弹的速度图可知,增大射弹的长径比或空化器长度应该有利于提高超空泡的减阻效果。
在图5中,用虚线将空化数σ=0时的阻力系数Cd0与各工况的拟合公式相连,可知函数Cd在σ全域中存在奇点,而且变化趋势不同:虚线随着σ的增大呈减小的趋势,实线随着σ的增大而增大。Cd0的数据一般是在水洞中获得的,拟合曲线是根据射弹实验数据获得的,现在在一张图上出现了两者的不匹配,这引出两个需要注意的问题:①从全湿状态经历局部空化到超空化的过程是不稳定的,在此范围内从实验中获得的阻力的时间平均值是否能代表真实的阻力?②式(3)和式(4)多项式的系数比较分散,是否能找到归一化的关系式?Logvinovich考虑到了超空泡流含有附加质量,超空泡携带的能量的一部分耗散在湍流尾迹之中,因此射弹的阻力系数增加, 变成Cd0乘以一个放大系数(1+σ), 即式(2);然后Reichardt和Munzner将放大系数修正到二次方项,即式(1)。但是,若要在Cd和σ域中将实验数据归一化整理,还缺乏力学理论的支撑。

图5 阻力系数随空化数变化
3 数值模拟
利用Gambit对三维计算域进行网格划分,如图6所示。对射弹体周围的流场以及自由面附近进行网格局部加密,设置最上方为压力出口,最下方为压力入口,侧面及射弹表面为固体壁面。对射弹体周围的流场以及自由面附近进行网格局部加密,应用动网格技术,网格划分完毕后约为25万左右。考虑重力影响,采用VOF多相流模型,即空气、水蒸气和水三相。算法采用PISO耦合算法,湍流模型采用RNGk-ε模型,设置水相由于空化变为水蒸气,水的饱和蒸汽压力取为20 ℃下的2 338.8 Pa。通过定义Patch设置了各个区域的初始相图,如图7所示,图中下部区域为水相,上部区域为空气相。时间步长设为10-5s,每20步自动保存。

图6 计算域网格划分 图7 流场初始相图
图8是工况2、长径比为11的弹体出水过程的三维数值计算结果,相邻两幅图片的时间间隔为1 ms。
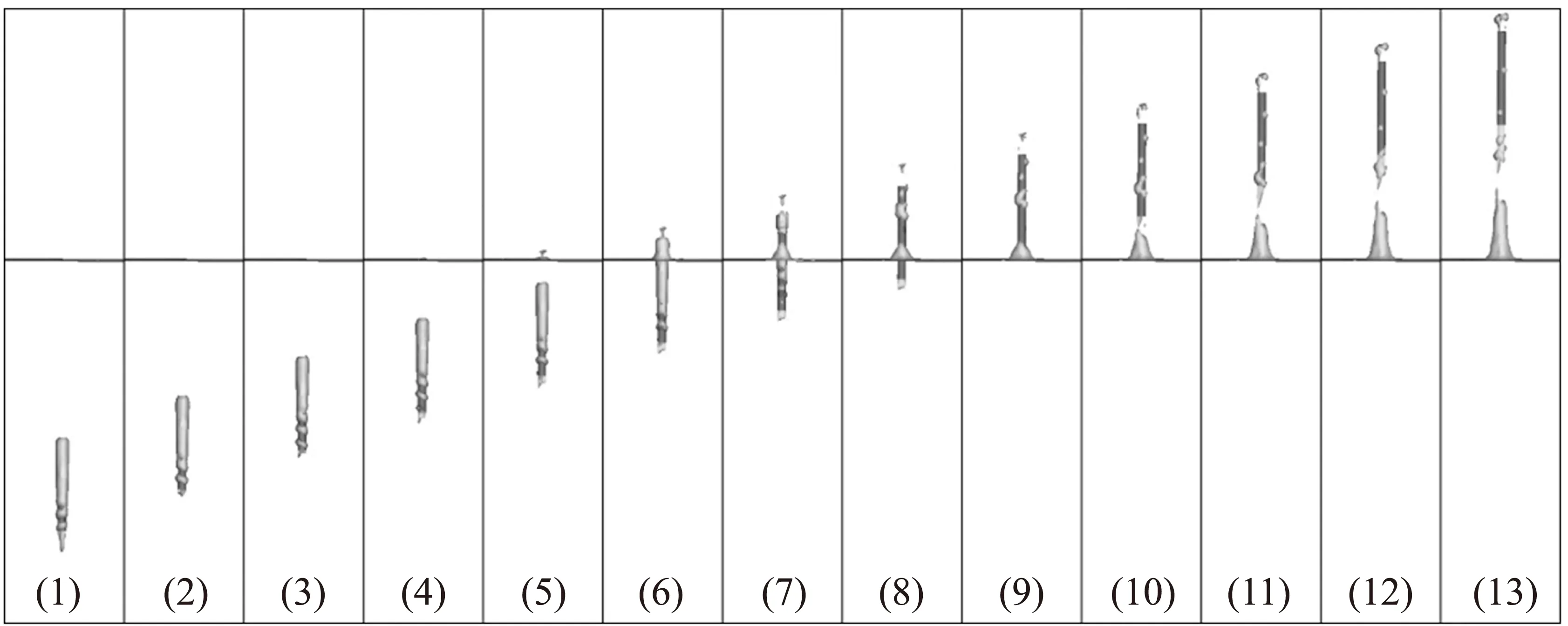
图8 工况2、长径比为11的弹体出水过程三维数值模拟结果(Δt=1 ms)
从图8中可见,由于细长体的速度不断降低,空泡在不断脱落。在图8(1)中细长体的尾部与水沾湿接触,头部覆盖着局部空泡;从图8(2)~8(5),空泡呈螺旋状不断脱落之后,弹体开始冲出水面进入到空气中;在图8(8)~8(13)中,可知弹体在出水的同时带出了喷溅的水花,甚至部分水花运动到了弹体的上方。对长径比为15的弹体的三维数值计算也给出了类似的结果[20],而这些结果在实验中同样被观察到了。因为采用的是动网格技术,弹体穿越自由面前后的速度变化的实验数据被作为已知条件代入程序,所以数值模拟结果与实验结果是完全一致的。
4 弹道偏转及超空泡的减阻作用
如第2小节所述,射弹在水下与超空泡壁面的碰撞、滑移有可能引起弹体出水后弹道轨迹的偏转。事实上,射弹在水下与超空泡壁面的碰撞、滑移,最可能引起水中弹道的偏移。图9给出了一例30°锥角头型弹体在水中偏转、翻滚,然后反向运动,最终没能出水的情况。影响弹道轨迹的因素,除了初始发射状态之外,还有弹头的抗干扰能力。实验发现,平头弹体的水中弹道稳定性是最好的,而锥角头型弹体抗干扰能力弱的原因,还需要理论上的分析。这里所说的弹道稳定性,是指射弹保持直线运动的能力。干扰可能来自多方面,例如,尾迹旋涡的脱落[21],弹体与空泡壁面的碰撞,等。
图1中已给出了工况1射弹模型的尺寸,现在在该射弹的中间开一个深1 mm、宽2 mm的凹槽,然后进行相同条件下的发射实验,实验结果如图10所示。可以看到,圆柱体在水中被超空泡完全包裹,直到空泡溃灭;随后的出水过程也很顺利。在全沾湿的情况下,表面凹槽肯定会增加弹丸的阻力,但是它一旦被空泡包裹住,弹丸表面几何形状的影响就消失了。对阻力系数的测量[20],证实了凹槽射弹与光滑射弹的阻力系数基本相同(见图5(a))。

图9 直径为6 mm、长径比为8、锥角30°弹体出水过程高速摄影照片(v0=40.13 m/s,Δt=0.2 ms)

图10 长径比为8、中部开有凹槽(深1 mm、宽2 mm)的圆柱体出水过程高速摄影照片(v0=41.07 m/s,Δt=0.4 ms)
5 结论
水的密度约为空气的800多倍,因此射弹在水中受影响的力学状态及弹道问题要比射弹在空气中飞行时的空气动力学问题复杂得多。射弹与超空泡壁面的碰撞、滑移,射弹头部形状的抗干扰能力等都会影响弹道轨迹。从本文给出的几个实例可知,超空泡的崩溃也有不同的形式,如以空化尾迹的形式崩溃(图3),或者直接收缩崩溃(图10),要分析射弹穿过这些空泡壁面或空化云团时的受力状态就十分困难。从射弹实验中测得的阻力系数,应该在Cd和σ域中归一化整理,但还有待理论的指引。对出水三维流场的数值模拟,计算出了二维模拟所得不到的结果,如空泡的脱落、在出水后弹丸周围的水花飞溅等,这说明了进行三维流场计算是很必要的。
[1] 姚奕,聂永芳,冯林平.潜射导弹运载器水下发射关键技术研究[J].飞航导弹,2010(2):56-60. YAO Yi,NIE Yong-fang,FENG Lin-ping.The key technology research of submarine missile carrier launching underwater[J].Winged Missiles Journal,2010(2):56-60.(in Chinese)
[2] WAUGH J G,STUBSTAD G W.Water-exit behavior of missiles:part 1-preliminary studies:AD273717[R].China Lake,California:Underwater Ordnance Department,1961.
[3] XING-KAEDING Y,JENSEN G,PERIC M.Numerical simulation of water-entry and water-exit of a horizontal circular cylinder[C]//Proceedings of the 6th International Conference on Hydrodynamics.Beijing:The Chinese Society of Theoretical and Applied Mechanics,2004:663-339.
[4] NEAVES M D,EDWARDS J R.All-speed time-accurate underwater projectile calculations using a preconditioning algorithm[J].Journal of Fluids Engineering,2006,128(2):284-296.
[5] 鲁传敬,李杰.水下航行体出水空泡溃灭过程及其特性研究[C]//第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源教授诞辰110周年纪念大会文集.无锡:海洋出版社,2012:54-67.
[6] 王一伟,黄晨光,杜特专,等.航行体有攻角出水全过程数值模拟[J].水动力学研究与进展,2011,26(1):48-57. WANG Yi-wei,HUANG Chen-guang,DU Te-zhuan,et al.Numerical simulation of a submerged body exiting from water with an attack angle[J].Chinese Journal of Hydrodynamics,2011,26(1):48-57.(in Chinese)
[7] KARN A,DE R,HONG J,et al.Closure mechanisms of ventilated supercavities under steady and unsteady flows[J].J Phys:Conf Ser,2015,656:012145.
[8] KINZEL M,MONEY M,KRANE M,et al.Jet-supercavity interaction:insight from CFD[J].J Phys:Conf Ser,2015,656:012133.
[9] 施红辉.物体高速出水过程中的空化气液两相流流型研究[J].中国科学院大学学报,2016,33(2):271-276. SHI Hong-hui.Cavitating gas -liquid two-phase flow pattern in water exit a high-speed body[J].Journal of University of Chinese Academy of Sciences,2016,33(2):271-276.(in Chinese)
[10] 施红辉,高聚瑞,贾会霞,等.弹丸出水和入水动力学的实验研究[J].中国科学技术大学学报,2015,45(6):470-475. SHI Hong-hui,GAO Ju-rui,JIA Hui-xia,et al.Experimental research on the hydrodynamic processes of water exit and entry[J]Journal of University of Science and Technology of China,2015,45(6):470-475.(in Chinese)
[11] 罗格维诺维奇 Γ Β.自由边界流动的水动力学[M].施红辉,译.上海:上海交通大学出版社,2012:97-126. LOGVINOVICH G V.Hydrodynamics of free-boundary flow[M].SHI Hong-hui,trans.Shanghai:Shanghai Jiao Tong University Press,2012:97-126.(in Chinese).
[12] 孙士丽,孙义龙,胡竞中,等.圆柱体出水运动的自由面效应及水冢现象分析[J].计算物理,2013,30(2):187-193. SUN Shi-li,SUN Yi-long,HU Jing-zhong,et al.Free surface effect and spike of a cylinder piercing water surface[J].Chinese Journal of Computational Physics,2013,30(2):187-193.(in Chinese)
[13] 施红辉,罗喜胜.可压缩性和高速多相流动[M].合肥:中国科学技术大学出版社,2014:156-247. SHI Hong-hui,LUO Xi-sheng.Compressible and high-speed multiphase flows[M].Hefei:University of Science and Technology of China Press,2014:156-247.(in Chinese)
[14] SAVCHENKO Y N.Control of supercavitation flow and stability of supercavitating motion of bodies[C]//VKI Special Course on Supercavitating Flows.Brussels:NATO,2001:1-14.
[15] 施红辉,陈波,王昀.钝体超空泡倾斜地穿过自由面出水实验及数值模拟[J].实验流体力学,2016,30(5):29-35. SHI Hong-hui,CHEN Bo,WANG Yun.Blunt body obliquely through the free surface water supercavitation experiment and numerical simulation[J].The Experiment of Fluid Mechanics,2016,30(5):29-35.(in Chinese)
[16] 施红辉,周杨洁,彭立兵,等.伴随空化现象的细长体倾斜穿透水体过程研究[J].浙江理工大学学报,2016,35(3):392-397. SHI Hong-hui,ZHOU Yang-jie,PENG Li-bing,et al.Research on obliquely penetrating water of a slender body accompanying cavitation phenomenon[J].Journal of Zhejiang Sci-Tech University,2016,35(3):392-397.(in Chinese)
[17] 施红辉,周浩磊,吴岩,等.伴随超空泡产生的高速细长体入水实验研究[J].力学学报,2012,44(1):49-55. SHI Hong-hui,ZHOU Hao-lei,WU Yan,et al.Experiments on water-entry of high-speed slender body and the resulting supercavitation[J].Chinese Journal of Theoretical and Applied Mechanics,2012,44(1):49-55.(in Chinese)
[18] REICHARDT H,MUNZNER H.Rotationally symmetric source-sink bodies with predominantly constant pressure distributions[J].Arm.Res.Est.Trans,1950:50(1):1-7.
[19] 柯乃普 R T,戴利 J W,哈密托 F G.空化与空蚀[M].水利水电科学研究院,译.北京:水利出版社,1981:104-146. KNAPP R T,DAILY J W,HAMMITT F G.Cavitation[M].China Institute of Water Reources and Hydropower Research,trans.Beijing:China Water Press,1981:104-146.(in Chinese)
[20] 高聚瑞.垂直出水超空泡与自由面相互作用时的三维流场实验及数值模拟研究[D].杭州:浙江理工大学,2015:1-111. GAO Ju-rui.Three-dimensional experiment and numerical simulation study of the interaction between the vertical supercavitation water-exit and free surface[D].Hangzhou:Zhejiang Sci-Tech University,2015:1-111.(in Chinese)
[21] SHI H H,TAKAMI T.Hydrodynamic behavior of an underwater moving body after water entry[J].Acta Mechanica Sinica,2001,17(1):35-44.
Study on the Trajectory of High-speed Projectile Exiting From Water
HOU Jian1,SHI Hong-hui2,SUN Ya-ya2,GAO Ju-rui3
(1.Department of Weaponry Engineering,Naval University of Engineering,Wuhan 430033,China;2.College of Mechanical Engineering and Automation,Zhejiang Sci-Tech University,Hangzhou 310018,China; 3.Hangzhou Turbine Compressor Co.,Ltd.,Hangzhou 310022,China)
Based on the developed experimental device for high-speed projectile exiting from water,the development process of the supercavity,shedding and its interaction with free-surface during exiting from water of high-speed projectile were observed by a high speed camera.Based on the measured experimental data,the cavitation numberσand the drag coefficientCdof the underwater body were calculated,and the polynomial fitting-formula ofσandCdwere given by referring to the formulas of Reichardt,Munzner and Logvinovich.A general correlation relationship betweenσandCdwas obtained.If an angle of attack of the slender body presents during exiting from water,the collapse of asymmetric cavity can lead a deflection of trajectory.Increasing the aspect ratio and length of the body,the drag of the underwater body can be reduced.By using the FLUENT software and VOF method,the three-dimensional flow field of exiting-from-water process was numerically simulated.The computational results are in good agreement with the experimental results.An example for the deflection of underwater trajectory during exiting from water was given.The result shows that the collision and slippage between the underwater projectile and supercavity wall can lead to the deflection of underwater trajectory.
supercavitation;underwater trajectory;high-speed projectile;projectile exiting from water;drag coefficient;numerical simulation
2016-10-14
浙江省自然科学基金项目(LY16A020003);“十三五”海军装备预研项目
侯健(1964- ),男,教授,研究方向为舰炮武器水下发射及超空泡射弹。E-mail:501-hj@163.com。
施红辉(1962- ),男,教授,研究方向为超空泡流动,流体界面RM不稳定性,三维湍流边界层。E-mail:hhshi@zstu.edu.cn。
O352
A
1004-499X(2017)01-0051-06
