例谈双变量不等式解决策略

文︳杨映湘陈亚凡

例谈双变量不等式解决策略

文︳杨映湘陈亚凡

在平时的数学学习和高考中，我们经常会遇到一类含有双变量的不等式问题。由于变量多且复杂，学生感到很棘手，找不到突破点，解题的错误率非常高。其实，我们可以化双变量为单变量，再利用导数这个强有力的工具，往往能使问题迎刃而解。

一、分离变量

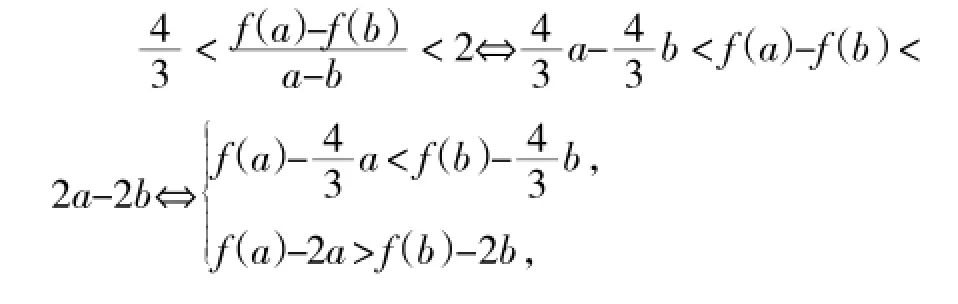
简洁性是数学的特性之一，因此，遇到多变量的时候，唯一目的就是化繁为简，而分离变量就是化繁为简的手段之一。利用分离变量这一方法处理双变量问题，一般情况下是式子两边变量形式比较对称，这样只需把变量分离到两边即可解决问题。

二、集中变量

如果变量不能分离出来，或者分离变量显得更麻烦，这个时候，我们需要考虑将双变量看成一个整体，利用整体换元的思想解决问题。

例2.已知f（x）=ex，求证：对任意x1，x2∈R，

证明：不妨设x1＞x2，

设g（t）=et-e-t-2t，（t＞0），则g′（t）=et+e-t-2≥

所以g（t）在（0，+∞）上单调递增，则g（t）＞g（0）=0，因此当t＞0时，et-e-t＞2t。从而原不等式成立。

题目中，x1，x2不好分离，因此，我们通过将变量x1，x2整体代换，使问题变成单元变量，从而得解。

三、固定其中一个变量作为参数

当分离变量、换元等方法都行不通的时候，我们可以考虑将其中一个变量作为参数，也可使问题得以解决。

例3.已知f（x）=xlnx，求证：当0＜a＜b时，0＜

证明：f（x）=lnx+1，

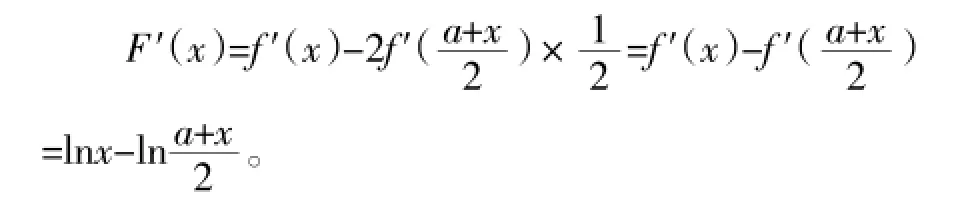
当0＜x＜a时，F′（x）＜0，当x＞a时，F′（x）＞0，

即F（x）在x∈（0，a）上为减函数，在x∈（a，+∞）上为增函数，

所以F（x）min=F（a）=0，又b＞a，所以F（b）＞F（a）=0，

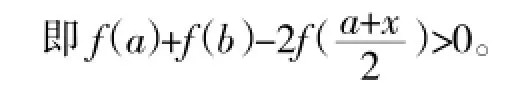
当x＞0时，G′（x）＜0，因此G（x）在区间（0，+∞）上为减函数；

因为G（a）=0，又b＞a，所以G（b）＜G（a）=0，

当然，解双变量问题远不止这些方法，需要灵活考虑。在处理这些问题时首先可以往以上思路上去想。比如下面这个题目：已知函数f（x）=lnxma+m（x＞0），

（1）求函数f（x）的单调区间；

（2）若f（x）≤0在（0，+∞）上恒成立，求实数m的取值范围；

（3）在（2）的条件下，证明：对任意的0＜a＜ b，求证

我们不能用分离变量去处理，那又怎么解决呢？

（作者单位：长沙市明德中学）