基于SURF和矩阵乘法的超大规模遥感图像亚像素配准算法研究
2017-03-27徐全飞
徐全飞,冯 旗
基于SURF和矩阵乘法的超大规模遥感图像亚像素配准算法研究
徐全飞,冯 旗
(中国科学院上海技术物理研究所,上海 200083)
图像配准是一项基本而又非常关键的图像预处理技术。在很多应用领域,要求配准精度达到亚像素级。现有的相位相关法具有精度高、计算简单等特点,但是随着图像规模的增大,计算付出的时间代价是巨大的。本文提出基于SURF和矩阵乘法相位相关法的超大规模遥感图像亚像素配准算法,采用化整为零的方法,首先把整幅图像划分成不同区域,其次使用改进的Canny算法进行边缘分割,去除无用信息,再次使用SURF算法提取特征,最后在关键点周围使用矩阵乘法相位相关估计图像亚像素偏移量。实验表明本文提出的算法不仅提高了算法运行速度,同时也解决了图像尺寸太大导致一般计算机无法处理的问题。并且由于矩阵乘法相位相关的良好抗噪声特性,因此即使存在噪声,算法仍然可以获得较高的亚像素偏移量估计精度。
图像配准;SURF算法;矩阵乘法相位相关;亚像素
0 引言
图像序列分析和图像融合常常需要对图像进行配准,尽管在很多场合,像素级别的图像配准就可以胜任了。但是在遥感探测和生物医学图像处理等领域,需要图像的配准精度到达亚像素级。目前图像亚像素配准方法可以分为3大类:
1)扩展相位相关法:扩展相位相关法是在相位相关法的基础上发展而来,继承了相位相关法的优点,对灰度差和窄带噪声不敏感,因此被广泛应用于亚像素图像配准。扩展相位相关又分为时域求解法和频域求解法[1-2]。
2)基于插值的方法:基于插值的方法主要是通过灰度内插的方法获得亚像素级精度。包括相似性函数内插法和图像灰度直插法[3-4]。
3)解最优问题:解优化问题法就是工程上最优化方法,选用适当的数学模型,通过迭代运算逐步优化参数,通过逐步优化获得亚像素精度的配准[5-6]。
这些方法各有优缺点,结合国内外本领域的研究可以知道:
1)灰度插值法优点是精度高,缺点是计算量巨大,且性能依赖于内插算法的质量。
2)扩展的相位相关法在频域求解时配准精度高,计算量小。但是时域解法则性能较差,并且这种方法只能处理固定形式的图像变化,对于更复杂的非线性变换就无法到达配准效果。
3)解优化问题法最为灵活,可以支持各种变换模型,配准精度也比较高,但计算量大,且收敛概率和寻找全局最优化的概率都需要提高。
本文使用的矩阵乘法相位相关法是基于傅里叶变换的良好特性,具有较大的位移检测能力,计算简单,精度高等优点。
图像特征点提取大致可以分为两大类:一是基于模版匹配的算法,二是基于集合特征的算法。本文研究重点是点特征提取算法之一的SURF算法。SURF算法是对SIFT算法的一种改进,主要体现在SURF算法的速度更快,效率更高。而提取的特征和SIFT算法提取的基本相同[7-8]。
1 算法描述
1.1 SURF算法
SIFT算法并不完美,存在一定的缺陷,比如实时性不高,有时候特征较少和对边缘光滑目标无法精确提取特征点等。后来学者在SIFT算法的基础上对算法进行了改进,比较有影响力的就是Herbert Bay提出的SURF算法。该算法在特征点提取数量相当的情况下,其执行速度是SIFT算法的三倍以上。因此在一定的条件下可以满足实时性的要求。SURF算法主要包括4个主要步骤[7-10]。
1.1.1 构造Hession矩阵
构造Hession矩阵是SURF算法的核心问题。对于给定的(,),Hession矩阵的判别式计算如下:
本征值det(approx)为负,该点不是极值点;本征值det(approx)为正,该点是极值点。然后再进行关键点的精确定位。
1.1.2 构造图像尺度空间
SURF算法构造尺度空间的方法比较巧妙。在SURF算法尺度空间中,图像的大小一直不变,不同层的尺度是通过改变模板的大小来构造的。尺度大小可以通过相应的公式计算。基于这种巧妙的算法,SURF算法可以对尺度空间中多层图像并行处理,极大地提高了算法的效率。
1.1.3 特征点精确定位和主方向分配
通过Hession和极值检测到的极值点还需要剔除伪极值和边缘响应点,从而产生精确的极值点。
1.1.4 构造SURF特征点描述算子
SURF算法首先将坐标轴旋转为关键点的方向,以保证旋转不变性。然后以关键点为中心取一个正方形框,这个正方形框具有方向,方向是特征点的主方向。然后把这个正方形框分为16个子区域,统计每个子区域中Sd,S|d|,Sd,S|d|,这样就有4×4×4=64维的特征数据。比SIFT算法128维的描述算子减少了一半。
1.2 扩展相位相关法的亚像素图像配准


对其进行反变换,既可以估计出图像在行和列的亚像素偏移量估计值。但是这种方法只能估计出整像素的偏移量。为了达到亚像素级的偏移量估计,需要对相位相关法进行扩展。


2 基于SURF和矩阵乘法相位相关法亚像素配准算法
2.1 整体算法流程图
本文系统算法流程图如图1所示。算法包括2个流程:①预处理,首先由于遥感图像具有较大的尺度,想对整个图像进行亚像素配准,需要的计算内存和计算时间将十分巨大,因此需要对海洋遥感图像进行分块。其次因为海上目标只占数据中极小部分,其他大部分是无用信息,因此使用改进的Canny算子进行边缘提取。然后在边缘提取后的图像中使用SURF算法进行特征点匹配,寻找配准最好的特征点。然后以配准最好的特征点为中心,在参考图像和待配准图像分别提取250×250的区域。②矩阵乘法相位相关,首先使用传统的相位相关法计算参考图像和待配准图像的互相关,并搜索互相关最大值的位置,因此可以图像整像素的平移量。然后上采样相关图像,上采样倍数是,其次计算上采样后的三矩阵相乘的输出矩阵,最后在输出矩阵(1.5,1.5)基础上,搜索相关最大位置。通过以上步骤可以精确的计算出图像的亚像素平移。
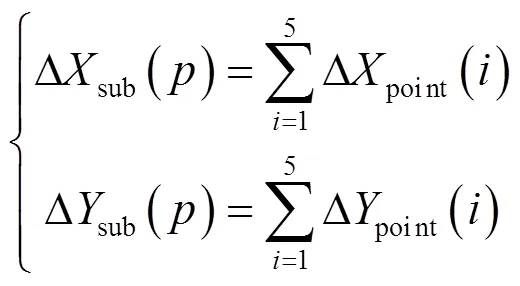
式中:Dsub()和Dsub()作为这子块图像的亚像素偏移量的估计值。最后把计算出来的所有的分块图像的Number个估计值再求平均值作为整幅图的亚像素偏移量的估计值:
因此本论文主要包含3个主要问题:
1)基于改进Canny算子的图像边缘检测算法;
2)基于SURF算法的图像点特征提取;
3)基于矩阵乘法相位相关法的图像亚像素配准;
下面将详细介绍论文中使用的3个算法并进行实验验证。
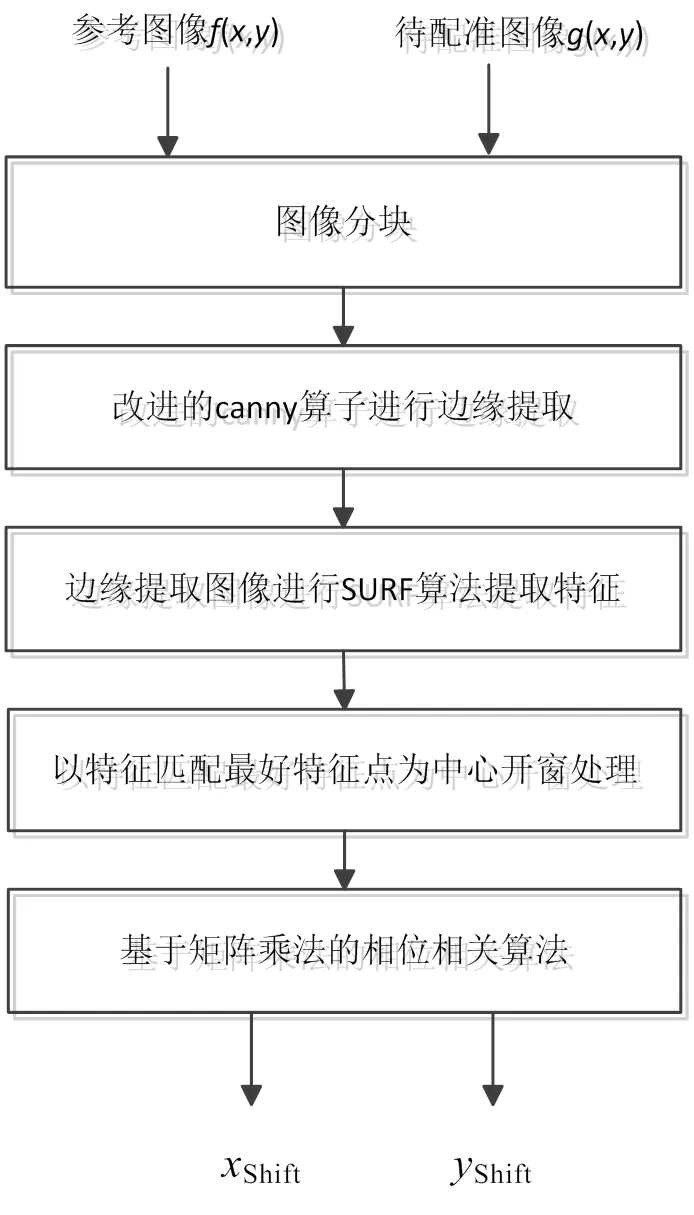
图1 系统算法流程图
2.2 基于改进Canny算子的图像边缘检测算法
海洋遥感图像具有图像空间分辨率高,图像信息丰富,目标特征明显,容易被人眼所解读和理解。由于遥感图像具有较大的尺度,且海上目标只占数据中的极小部分,其他大部分是无用信息,因此可以使用边缘检测算法对图像进行边缘提取。
自从1986年Canny提出来最佳边缘检测算子——Canny边缘检测之后,人们开始围绕Canny算子图像边缘检测的各种算法展开研究工作,各种边缘检测算法应该满足以下3个准则,即:信噪比准则、定位精度准则和单边缘响应准则。由于传统的Canny算子需要人为的设定高低阈值,需要反复多次实验才能找到合适的阈值,且高低阈值的比例是一个固定值。为了克服传统Canny算子的上述缺点,本文提出自适应双阈值Canny算子。本文使用最大类间方差法来确定自适应阈值。因此基于改进Canny算子的图像边缘检测算法流程如下:
1)对图像进行平滑处理,用高斯滤波器抑制噪声;
2)计算方向导数,并利用方向导数的计算结果计算梯度;
3)对梯度进行非极大值抑制;
4)用OTSU算法进行阈值检测;
5)输出图像边缘检测图像。
2.3 基于SURF算法的图像点特征提取

2.4 基于矩阵乘法相位相关法的图像亚像素配准
基于矩阵乘法的相位相关法使用了由粗到精的计算方法。1)粗定位,如图2中(a)所示,首先使用传统的相位相关法来估计出图像整像素的偏移量(ShiftInteger,ShiftInteger)。2)精细定位,如图2中(b)所示,利用基于矩阵乘法的DFT获取粗定位点(ShiftInteger,ShiftInteger)的1.5×1.5领域内倍采样后的区域,通过计算上采样区域的相位相关得到像素级的平移量(UpShiftInteger,UpShiftInteger),由于是上采样倍得到的像素级平移量,因此亚像素的偏移量是(UpShiftInteger/,UpShiftInteger/)。综上所述,图像的平移量(Shift,Shift)是:

3 算法实验验证
3.1 改进的Canny算法优势
图3是使用传统Canny算法和改进的基于OTSU的Canny算法处理得到的图像,从图3上可以看出来,传统的Canny算法很多真正的边缘没有检测出来,边缘提取图像质量严重退化,基本分辨不出真实目标的轮廓。效果如图3(b)所示。而改进的Canny算法不仅有效地提取了清晰容易分辨的图像的边缘,而且有效抑制了虚假边缘的产生,有效提高了边缘提取的精度和准度,如图3(c)所示。


图3 传统Canny算法和本文改进的Canny算法效果对比
3.2 特征点数量和SURF阈值关系
特征点提取数量和阈值有很大关系。如图4所示,当阈值比较大时提取的特征点较少,但是特征点都是比较明显的特征;而阈值比较小时提取的特征点较多。圆半径大小代表尺度大小,圆形中心代表特征点坐标,线代表特征点方向。提取特征点后,就可以在特征点中寻找匹配最好的若干个特征点,分别在选取的特征点周围进行开窗运算。特征点数量的选取和开窗大小可以由实验确定。
3.3 特征点数量Q和开窗大小W选取
特征点数量的选取和子图的大小以及特征点的质量都有很大关系。特征点选取过多,不好的特征点也参与到亚像素偏移量的估计,必然导致较大误差。图5中c和d子图中3条线从上到下依次为在在特征点周围开窗大小分别为250,300,350。由图可以知道在开窗大小比较小情况下,特征点数量的选取对偏移量的影响随着特征点的增加波动而减小,在列方向偏移量估计随着特征点的变化误差波动比较大,但是估计误差都在0.055个像素之内。而在行的方向上,情况明显好转,当行方向特征点数量增加时,偏移量的估计误差均在0.06个像素之内。且随着特征点数量的增加误差逐渐变小。因此在保证算法偏移量估计的准确性的基础上,特征点选取的越少越好,这不仅可以提高算法偏移量估计值的精确性,而且也可以提高运算的速度。
对于选取开窗大小的问题可以从图5中(a)和(b)中获得启发。由图可以知道特征点周围开窗大小对与亚像素图像偏移量估计值影响很大,在开窗大小比较小的时候,图像的偏移量估计误差最高到达0.4个像素,随着开窗大小的变大,图像的估计误差减小达到0.05之内。由图示可知,在特征点周围开窗大小为250、300、350时,行方向偏移量估计误差在0.06个像素之内,而列方向偏移量估计误差也在0.06个像素之内。但是随着特征点周围开窗大小的变大,计算时间增加。综合以上的讨论,可以得出在特征点数量可以在小于6时任意取值,都能保证列的误差在0.06个像素之内。特征点周围开窗大小=5时候可以获得比较好的偏移量估计精确值和较快的计算时间。实验中=5,开窗大小为250×250。

图4 SURF算法中阈值和提取特征点数量关系
3.4 噪声对算法的影响
图像亚像素偏移量是由于图像下采样导致的。因此对图像先插值然后在进行整像素的平移。最后下采样图像将产生亚像素偏移。比如先插值100倍,然后平移5个像素,在下采样图像,将获得0.05个像素偏移。实验中使用的图像是成像光谱仪可见光图像,图像大小是8000×8192。首先使用重采样的方式获得图像偏移量。分别是∆1=(10.875,5.375)和∆2=(2.583,3.417)。理想图像和平移后测试图像如图6所示。
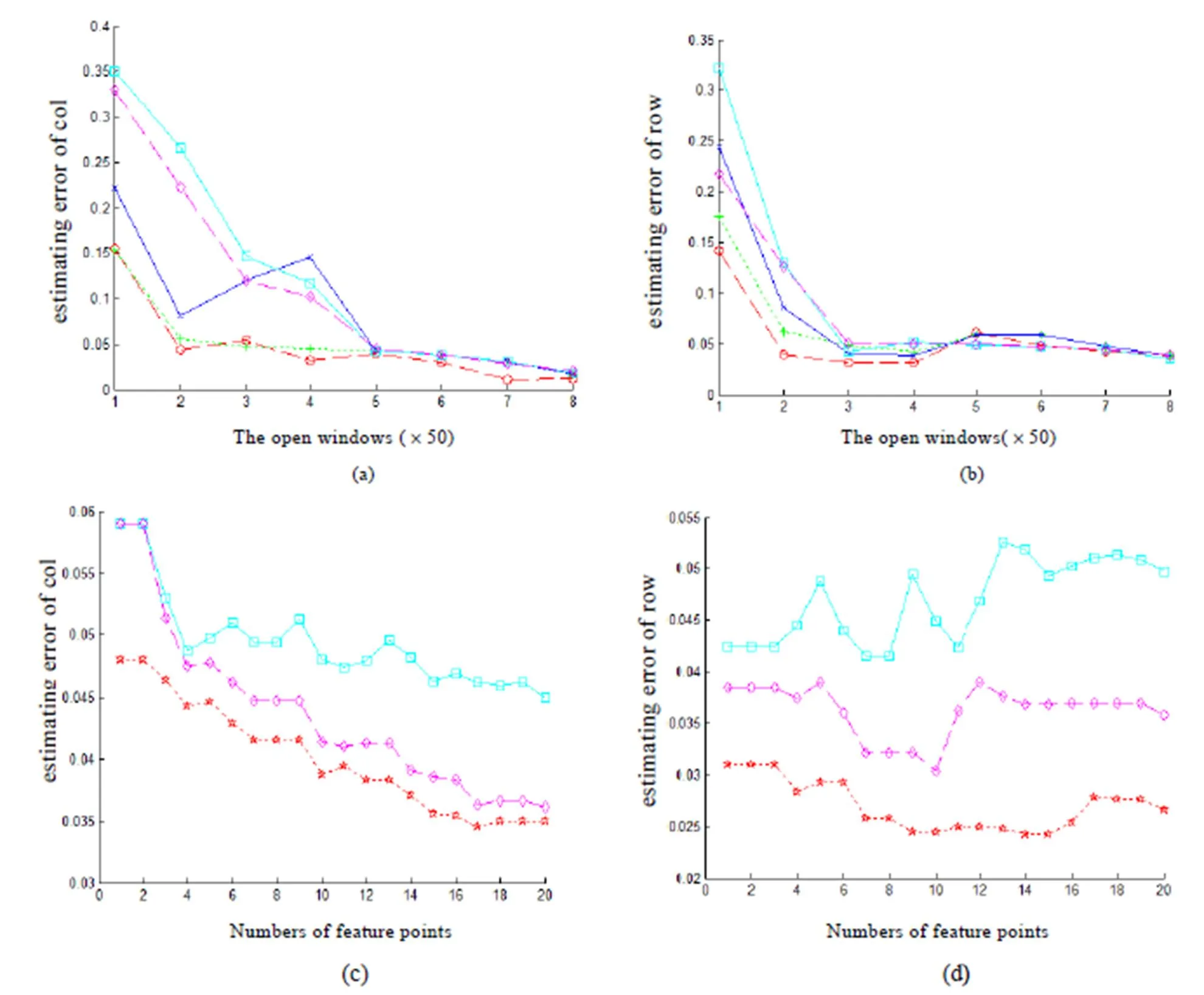
图5 特征点数量开窗大小和图像亚像素偏移量估计误差关系
如图7所示,为了研究噪声对算法偏移量估计值精度的影响,对理想的图像平移后分别添加不同的高斯噪声,添加噪声后,图像信噪比分别为5,10,20,30,40和50。分别使用基于扩展相位相关法、基于插值的亚像素配准算法、基于最优问题的算法和本文基于改进的矩阵乘法相位相关法分别计算图像的亚像素偏移量。由表1可以看出在无噪声理想情况下,4种算法都取得了高精度的偏移量估计值,随着图像噪声逐渐增加,基于扩展相位相关法、基于插值的亚像素配准算法和基于最优问题的算法偏移量估计精度退化严重,当信噪比大于40时候,3种算法的偏移量的估计误差小于0.1个像素值,而当图像的信噪比小于40后,图像亚像素偏移量误差变大,最大误差0.6个像素左右,这个误差是不可以接受的。而本文提出的算法当图像信噪比大于10的时候,图像亚像素偏移量估计误差在行列方向均优于0.06个像素。当图像的信噪比为10时图像亚像素偏移估计误差在行方向上为0.05个像素,列方向上为0.07,均小于0.1个像素。在图像噪声比为5时候,图像的亚像素偏移估计误差偏差较大。由表1实验数据可以看出本论文提出的算法对图像的噪声有一定的容忍,在图像受噪声污染时候,仍然可以获得较高的亚像素偏移量的估计,因此本论文算法对于噪声图像的亚像素配准有一定的现实意义。
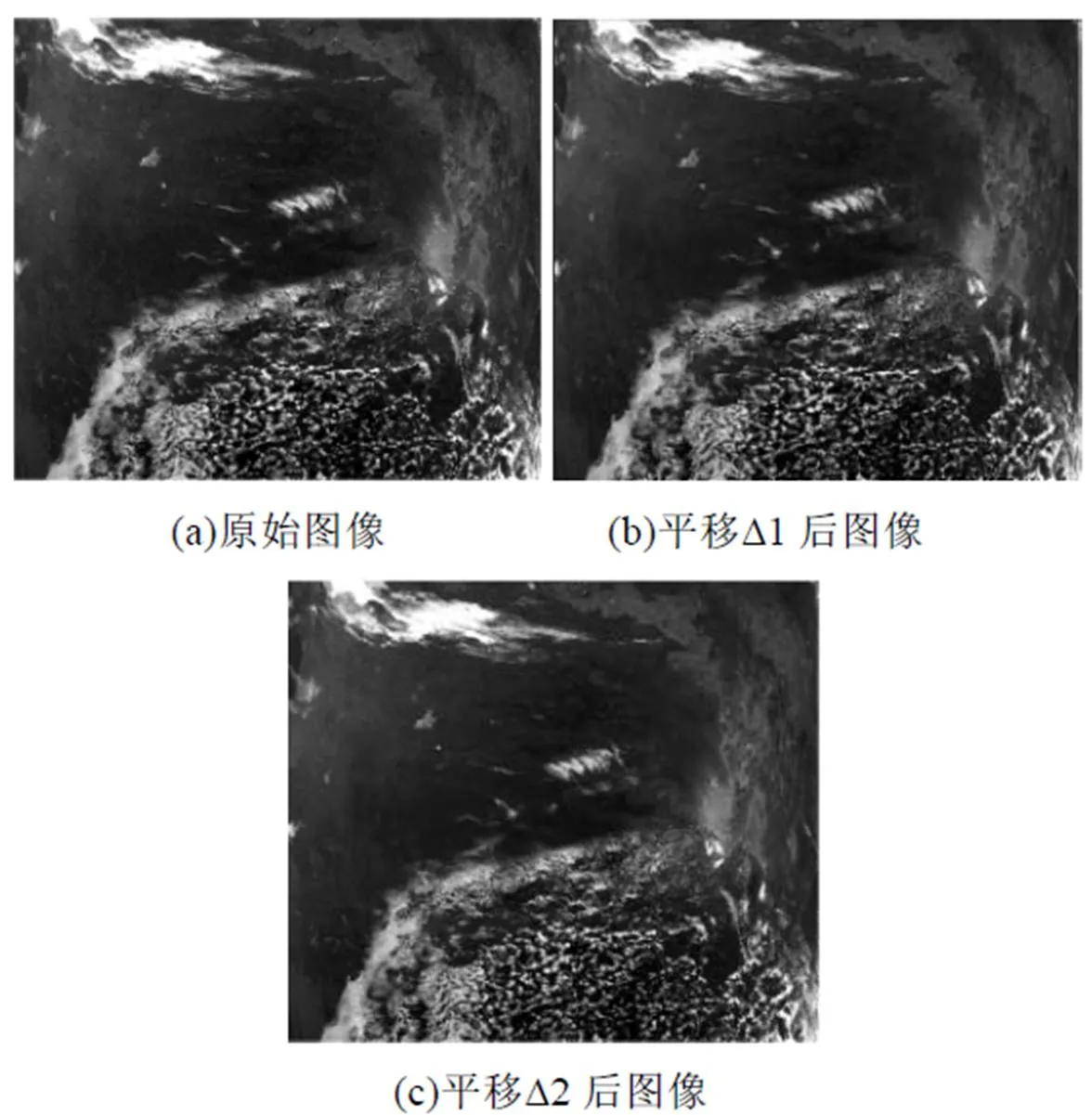
图6 理想图像和平移∆1和∆2的测试图像

图7 理想图像平移∆1后添加不同信噪比的高斯噪声

表1 不同信噪比下算法实验结果对比表
注:表1中A表示本论文提出的算法,B表示基于相位相关的亚像素配准算法,C表示基于插值的亚像素配准算法,D表示基于最优化方法的亚像素配准算法。
3.5 算法的运行时间
通过在win7,64位操作系统,Inter core i7-3770 3.4GHz 8G内存NVIDIA GeForce GT620平台下,使用Matlab2014a进行算法的实验仿真验证。图像的尺寸大小是8000×8192,图像的偏移是∆1=(10.875, 5.375)和∆2=(2.583, 3.417)。图像没有叠加任何噪声。表2中给出了实验的验证结论。由表2可知,本论文提供的基于SURF算法和矩阵乘法的超大规模遥感图像亚像素配准算法运行时间是基于相位相关的亚像素配准算法速度的4.5倍,是基于插值的亚像素配准算法速度的6.2倍,是基于最优化方法的亚像素配准算法速度的6.9倍。因此本论文提出的算法明显提高了亚像素图像配准的速度。
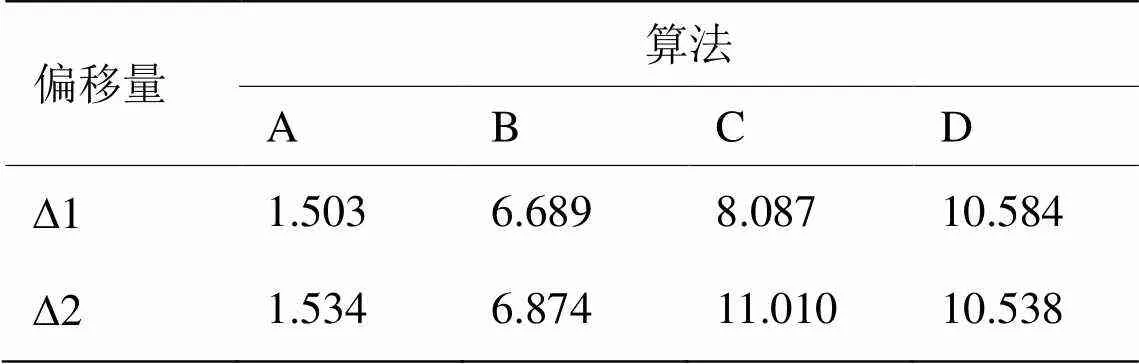
表2 不同算法运行时间对比表
注:表2中A表示本论文提出的算法,B表示基于相位相关的亚像素配准算法,C表示基于插值的亚像素配准算法,D表示基于最优化方法的亚像素配准算法;表中的数据的单位是秒(s)。
3.6 子快大小对程序运行时间和精度的影响
图像的子块大小对算法的运行时间和精度都有很大的影响,分块图像太大,处理需要的内存空间变得很大,分块图像太小,分块数量过多,亚像素偏移量估计精度将变低。因此需要在精度和速度之间做选择。在图像偏移量为∆1=(2.686,11.058)的时候进行实验验证。通过在win7,64位操作系统,Inter core i7-3770 3.4GHZ 8G内存NVIDIA GeForce GT620平台下,使用matlab2014a进行算法的实验仿真,实验结果如表3所示。由表3可知,随着子图像变大,算法的运行时间随着子图像尺度的变大而增加。因为随着子图像的尺寸增加,改进canny算法,SURF算法和基于矩阵相位相关所花时间增加明显,因此子图像的运行时间必然增加。图像亚像素偏移量估计的精度和子图像尺寸的大小的规律如图8所示。图8中-o表示列方向偏移量估计误差随图像分块大小变化曲线,-*表示行方向偏移量估计误差随子图像大小变化曲线。
由图8可以看出图像行和列的亚像素图像偏移量的误差变化规律极其相似。开始时候图像分块比较小,导致图像亚像素偏移量估计值误差比较大,列方向的误差最大值达到0.066左右,然后随着图像尺寸变大,图像的亚像素偏移量估计误差变小。当图像块的尺寸为2048的时候,图像的误差达到最小值0.01左右。再增大图像块的尺寸,亚像素偏移量估计误差和运行时间都在增加。因此图像的亚像素偏移量估计值误差和算法的复杂度成正比。因此需要在速度和精度上做均衡。
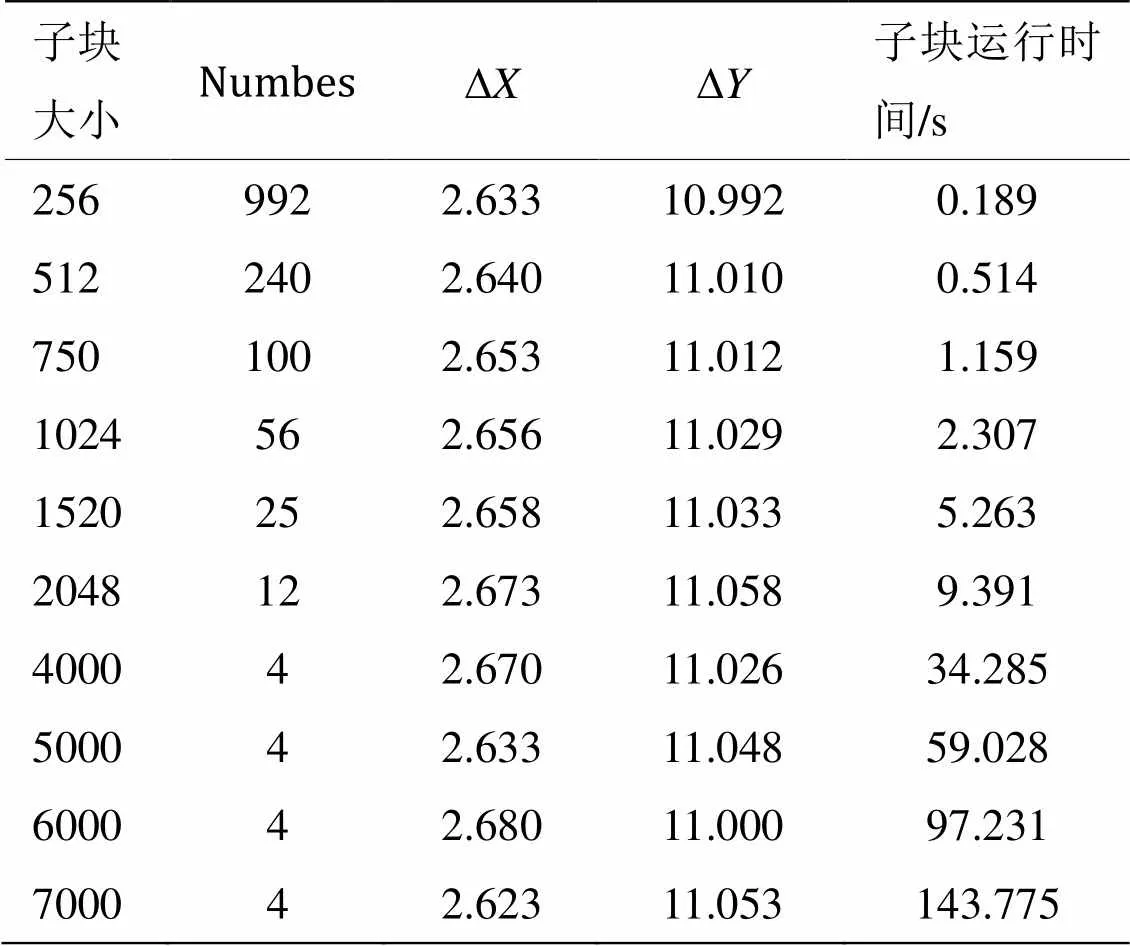
表3 不同大小子块图像本文算法实验结果表

图8 亚像素偏移量估计误差随图像子块大小变化
综上实验可以证明:本论文提出基于SURF和矩阵乘法相位相关法的超大规模遥感图像亚像素偏移量估计算法取得了较高的精度,满足实际应用需求。
4 结束语
相位相关法是一种广泛应用的亚像素图像配准算法,本论文提出一种新颖的基于SURF和矩阵乘法相位相关算法来应对超大规模遥感图像亚像素图像偏移量估计的困难。实验表明:对于超大规模遥感图像,本论文提供的算法的复杂度不高,通过选择合适的分块图像尺寸可以获得较高的图像亚像素偏移量和较少的算法运行时间,如果使用FPGA,DSP等器件进行并行处理时,可以满足实时处理要求。适合需要高精度、亚像素实时图像配准的场合,如扩展目标波前检测、高分辨成像等领域。本论文对于超大规模遥感图像的实时配准提供了一种行之有效的算法,对于超大规模遥感图像的后续处理和信息挖掘提供了必要的前提和条件。后期可以考虑使用FPGA或者DSP等器件进行并行处理,该算法将会表现出更优异的实时处理的效果。
[1] H. Foroosh, J. Zerubia, M. Berthod. Extensionof phase correlation to sub-pixel registration[J]., 2002, 11(3): 188-200.
[2] H.S. Stone, M. Orchard, E.-C. Chang, et al.A fast direct fourier-based algorithm for subpixel registration of images. IEEE Trans. Geosci[J]., 2001, 39(10): 2235-2243.
[3] HE Bin, LU Jinbo. Remote sensing image sub-pixel interpolation and fitting registration[J].:, 2012, 33(6): 686-690.
何斌, 禄金波. 遥感图像亚像素插值拟合配准方法[J]. 长春工业大学学报: 自然科学版, 2012, 33(6): 686-690.
[4] ZHOU Wu, HUYueming. Sub-pixel Image Registration Algorithm based on Phase Correlation and Image resampling[J].:, 2010, 38(10): 68-78.
周武, 胡跃明. 基于相位相关和重采样的亚像素图像配准算法[J]. 华南理工大学学报: 自然科学版, 2010, 38(10): 68-78.
[5] WANG Lingxia, HAO Hongxia. Remote sensing images sub-pixels registration algorithm by selecting best control points[J]., 2015, 31(3): 274-281.
王凌霞, 郝红侠. 最优控制点选取的遥感图像亚像素配准算法[J]. 信号处理, 2015, 31(3): 274-281.
[6] 金宏彬, 范春晓, 李永, 等. 基于人工交互的多模态图像亚像素配准[J]. 北京邮电大学学报, 2015, 31(3): 274-281.
JIN Hong-bin, FAN Chun-xiao, LI Yong et al. Sub-Pixel Multimodal Image Registration By Human Interaction[J]., 2015, 38(1): 11-15.
[7] D. G. Lowe. Distinctive image features from scale-invariant keypoints[J]., 2004, 60(2): 91-110.
[8] H. Bay, T. Tuytelaars, L. Van Gool. Surf: Speeded up robust features[C]//, 2006:404-417.
[9] 葛盼盼, 陈强. 基于SURF特征提取的遥感图像自动配准[J]. 计算机系统应用, 2014, 23(3): 16-24.
Ge pan-pan, Chen Qiang. Remote Sensing Image Automatic Registration based on SURF Feature Extraction[J]., 2014, 23(3): 16-24.
[10] 冯亦东, 孙跃. 基于SURF特征提取和FLANN搜索的图像配准算法[J]. 图学学报, 2015, 36(4): 650-654.
FENG Yidong, SUN Yue. Image Matching Algorithm Based on SURF Feature Extraction and FLANN Search[J]., 2015, 36(4): 650-654.
[11] 陆凯, 李成金, 赵勋杰, 等.一种快速的亚像素图像配准算法[J]. 红外技术, 2013, 35(1): 27-33.
LU Kai, LI Chengjin, ZHAO Xun-jie, et al. A Fast Sub-pixel Image Registration Algorithm[J]., 2013, 35(1): 27-33
[12] 樊志华, 王春鸿, 绕长辉, 等. 基于Harris角点量与相位相关的亚像素级图像配准方法[J]. 计算机应用研究, 2011, 28(2): 788-791.
FAN Zhi-hua, WANG Chun-hong, RAO Chang-hui et al. High accuracy subpixel image registration based on phase-only correlation of Harris strength[J]., 2011, 28(2): 788-791.
Sub-pixel Registration of Very Large Scale Remote Image Based on SURF and Matrix Multiplication Algorithm
XU Quanfei,FENG Qi
(Shanghai Institute of Technical Physics of The Chinese Academy of Sciences,Shanghai 200083, China)
Image registration is a basic and important image preprocessing technology. In many applications, it is needed to extend the image registration to sub-pixel level. The existing phase correlation algorithm has advantages of easy calculation and high accuracy; however with the increasing scale of the image, the time cost of calculation is huge. This paper proposes a sub-pixel registration algorithm of very large scale remote sensing image based on SURF and matrix multiplication phase correlation. This algorithm adopts the method “breaking up the whole into p- arts”. First, the whole picture is divided into different regions. Secondly, the improved Canny algorithm is used to segment the image, removing the useless information. Thirdly, the feature is extracted by the SURF algorithm again. Finally, the sub-pixel offset is calculated by the matrix multiplication phase correlation around the feature points. According to the experiment, the proposed algorithm can not only improve the operating speed, but also solve the problem caused by general computer cannot handle so large pictures. At the same time, due to the good anti-noise characteristic of matrix multiplication phase correlation, even if there is noise, the algorithm can still get a high-accuracy estimation of sub-pixel offset.
image registration,SURF algorithm,matrix multiplication phase correlation,sub-pixel
TP751.1
A
1001-8891(2017)01-0044-09
2016-04-05;
2016-05-26.
徐全飞(1989-),男,河南新蔡人,博士研究生,主要从事超大规模遥感图像处理、模式识别及硬件实现。
全球变化与海汽相互作用专项(GASI-03-03-01-01)。
