三维空间中线结构光与相机快速标定方法
2017-03-27陈文亮董清亮王向军吴凡路
陈文亮,董清亮,刘 峰,王向军,吴凡路
三维空间中线结构光与相机快速标定方法
陈文亮,董清亮,刘 峰,王向军,吴凡路
(天津大学微光机电系统技术教育部重点实验室,天津 300072)
针对结构光立体视觉系统快速标定问题,本文提出了一种多线结构光单目视觉测量系统的快速标定方法,该方法可以同时完成多个线结构光的标定,不必每一个线结构光单独标定,从而实现相机与线结构光的快速标定。具体为相机内参采用张氏标定法提前标好,外参标定采用设计的三维阵列立柱靶标配合实现。在已知三维阵列立柱靶标各立柱端面中心点对应物像坐标后,可得到二者间的旋转和平移矩阵;在线结构光投射到对应不同高度立柱端面上后,根据以上物像关系可得到端面光条坐标,利用该坐标可拟合出激光平面方程,进而可建立起各激光面与相机之间的变换关系,完成系统标定。
三维阵列立柱靶标;线结构光;相机标定;平面方程
0 引言
常见的视觉测量系统有双目测量系统、基于结构光的单目视觉测量系统以及基于点光源的测量系统[1]。其中线结构光单目视觉测量技术具有结构简单、精度较高、速度快等优点,并且在在线测量、三维地貌测量等领域有广泛的应用,所谓的线结构光是指面激光。本文就基于线结构光单目视觉测量中的标定进行研究。标定的参数包括摄像机的内外参以及线结构光平面方程,其中摄像机的内参包括焦距、中心点坐标、径向畸变、切向畸变,都以像素为单位,外参包括平移矩阵与旋转矩阵,表示像平面坐标系与世界坐标系之间的关系。
在线结构光标定中,由于线结构光平面不同于机械平面,很难确定线结构光平面上某点的世界坐标系下的坐标。所以对线结构光进行标定具有一定的困难。针对线结构光的标定方法主要有细丝散射法[2]和锯齿靶标法[3]等。但这几种方法需要精密的辅助设备,而且过程比较复杂,不适合现场标定。Huynh等提出基于三维靶标的交比不变标定方法[4],该方法精度较高,但标定过程中难以获得高质量标定图像。此外现在有利用辅助激光的棋盘格靶标标定方法[5]、基于圆形靶标的线结构光标定方法[6],这些方法操作复杂,不利于现场标定。裘祖荣,陈培芬等人提出一种多线结构光标定方法[7],但该方法是用于小测量区域,而且对世界坐标系与激光传感器的相对位置有一定的要求。本文提出了一种多线结构光单目视觉测量系统的快速标定方法,在该标定方案中,相机的内参采用张正友的标定方法。相机的外参标定与线结构光标定均采用三维阵列立柱式靶标。同时该靶标能够解决线结构光平面上点难以获取得问题,该种靶标制作简单,摆放方便,适合现场标定。
1 线结构光测量数学模型
线结构光测量的数学模型如图1所示,其中c-ccZc为摄像机坐标系,o-oo为计算机坐标系,-为像平面坐标系。设为线结构光与被测物体的某一交点,在世界坐标系下的齐次坐标为w=(w,w,w, 1)T,在摄像机坐标系与计算机坐标系下的对应点的齐次坐标分别为c,p²,该点在像平面坐标系下对应点的坐标为¢=(,, 1)T,根据透视变换[8],可得:
*¢=**w=*w(1)
式中:矩阵,分别为相机的内参与外参,为一任意比例尺度因子,无特殊含义。设线结构光在世界坐标系下的平面方程如下:
*w+*w+*w=1 (2)
由公式(1)与公式(2)可得到一个四元一次方程组,如下所示:
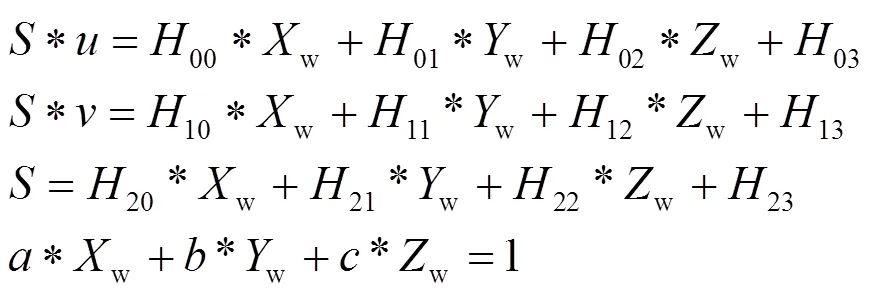
如果摄像机的内参、外参以及线结构光在世界坐标系下的平面方程已知,就可以根据方程组(3),由线结构光的像平面坐标得到该对应点在世界坐标系下的坐标,如下所示:

其中:
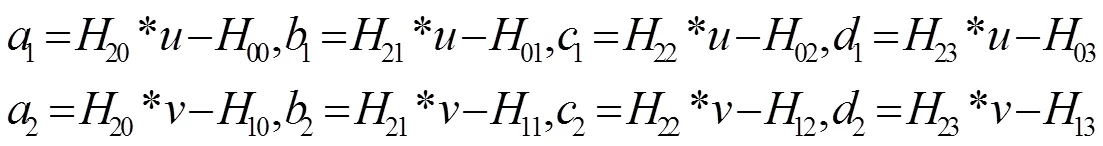
如果能够同时获得多个激光面在世界坐标系下的平面方程,每一个线结构光对应一个四元一次方程组,即可同时完成对多个线结构光的标定。
2 相机以及线结构光的标定
2.1 相机内参标定
内参标定采用张氏标定方法,采用棋盘格作为标定靶标,如图2所示。可以得到相机的焦距、图像中心点坐标以及畸变系数。由此得到相机内参。

图2 棋盘格靶标
2.2 相机外参标定
在该方案中,采用三维阵列立柱式的靶标。图3为标定靶标示意图。在该靶标中,分布有高低不同的立柱,每一个立柱端面中心点在世界坐标系下的坐标是已知的。在图像中,可以获得每一个端面中心点的在像平面坐标下的坐标。通过两者的对应关系,解得相机的外参。
2.3 线结构光标定
在标定相机外参之前,确保每一条线结构光能够打在高低不同的立柱上,如图3所示。这样,就会在立柱端面有线结构光线条,如图4所示。
由于已经标定出相机的内参与外参,便可以得到公式(1),同时每一个立柱的高度是已知的,设立柱的高度为w,则可以通过线结构光线条上点的像平面坐标系下的坐标,通过方程组(6)求得该点在世界坐标系下的坐标:

如图3所示,每一个线结构光在高度不同的立柱端面上形成激光线条,通过方程组(6)求得每一个激光线条上点的世界坐标,然后利用最小二乘法,拟合线结构光平面,得到线结构光在世界坐标系下的平面方程,完成对线结构光的标定。
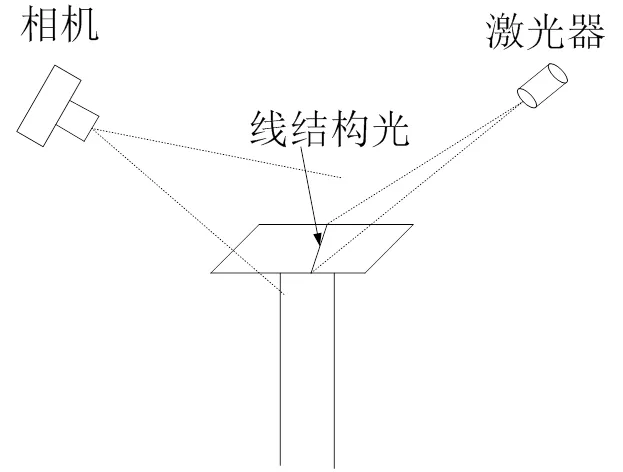
图4 立柱端面激光线条
3 实验验证
在该实验中,同时对两条线结构光进行标定,采用的激光器为532nm的绿激光器和650nm的红色激光器,功率分别为15mW和10mW。实验采用的为BALSER相机,型号为scA1600-14gm。分辨率为1628×1236,CCD尺寸为1/1.8²,像素尺寸4.4mm×4.4mm。
3.1 相机内参标定
采用MATLAB相机标定箱对相机的内参进行标定,在视场不同位置取图片,如图5所示。一共取了60幅棋盘格图片进行标定,标定的结果如表格1所示,其中u、v、0、0单位为像素。1,2为径向畸变,1,2为切向畸变。
3.2 相机外参标定
在标定外参时,需要特定的三维阵列立柱靶标,在该实验中,通过在光学平台上摆放立柱,构成标定所需要的三维阵列立柱靶标,如图5所示。标定外参时,需要图片上点的像素坐标以及对应点在世界坐标系中的坐标。其中对应点的世界坐标由三坐标测量机测得,三坐标测量机的测量精度为15mm。当完成测量后,对靶标取图片,通过读图片,获得对应点的像素坐标。这样就得到了立柱端面中心点的世界坐标与像素坐标。通过两者之间的对应关系来获得旋转矩阵与平移矩阵。该靶标共有12个立柱,每一个线结构光对应六个立柱,其中的4个立柱用来标定,另外两个用来做精度校验。
标定得到的旋转矩阵与平移矩阵分别为矩阵(7)与矩阵(8):

图5 棋盘格图片位置

表1 相机标定结果


3.3 线结构光标定
然后对摆放的立柱取图片,立柱摆放如图6所示。其中每一个线结构光对应有不同高度的6个立柱,每一条线结构光分别打在对应的高度不同的立柱上。其中4个立柱用来拟合线结构光平面,另外两个立柱作为精度校验柱,真值由三坐标测量机测得。完成相机内外参标定之后,就可以得到公式(1),由于每一个立柱的高度是已知的,这样,就能够通过立柱端面上线结构光的像素坐标,通过方程(6),得到线结构光线条上点在世界坐标系下的三维坐标。得到不同高度立柱上点的坐标后,利用最小二乘法,便可以完成线结构光的平面拟合,拟合的平面方程如下:
0.671×10-3×+0.130×10-1×-
0.300×10-1×=1 (9)
0.145×10-3×+0.511×10-2×-
0.102×10-1×=1 (10)
其中公式(9)为第一条线结构光在世界坐标系下的平面方程。公式(10)为第二条线结构光在世界坐标系下的平面方程。
4 精度评定
完成线结构光的标定之后,每一条线结构光都对应一个方程组(3),这样,就可以通过像平面坐标系下的坐标,求得世界坐标系下的坐标。然后,通过两个校验柱,对每个线结构光标定结果进行精度校验,数据如表2与表3所示。其中的真值用三坐标测量机测得。其中相对误差为0.57%。

图6 实验现场图片
5 结论
该文中提出的多线结构光单目视觉测量系统的快速标定方法,分为相机内参标定,相机外参标定,线结构光标定。其中相机的内参采用棋盘格靶标进行标定,相机的外参与线结构光均采用三维阵列立柱靶标进行标定。三维阵列立柱靶标制作摆放方便,结构简单,解决了线结构光上的点的世界坐标难以获取的问题,并采用最小二乘法拟合线结构光平面。实验结果证明:相对误差为0.57%。

表2 第一条线结构光实验两个校验点测量结果

表3 第二条线结构光实验两个校验点测量结果
[1] 张勇斌, 卢荣胜, 费业泰, 等. 基于十字线结构光视觉测量系统[J]. 计算机测量与控制, 2004, 12(1): 13-14.
ZHANG Yong-bin, LU Rong-sheng, FEI Ye-tai, et al. Vision Inspecting System Based on Cross Structured Light[J].. 2004, 12(1): 13-14.
[2] 崔希民, 李聪, 袁得宝, 等. 基于拉丝法的线结构光视觉测量系统标定[J]. 科技导报, 2014, 32(24): 65-67.
CUI Xi-min, LI Cong, YUAN De-bao, et al. Calibration of a Line Structured Light Vision Measuring System Based on the Drawing Method[J]., 2014, 32(24): 65-67.
[3] 段发阶, 刘凤梅, 叶声华. 一种新型线结构光传感器结构参数标定方法[J]. 仪器仪表学报, 2000, 21(1): 108-110.
DUAN Fa-jie, LIU Feng-mei, YE Sheng-hua. A New Accurate Method for the Calibration of Line Structured Light Sensor[J]., 2000, 21(1): 108-110.
[4] 王金桥, 段发阶, 伯恩, 等. 线结构光扫描传感器结构参数一体化标定[J]. 传感器学报, 2014, 27(9): 1197-1120.
WANG jin-qiao, DUAN Fa-jie, BO En, et al. Calibration of Line Structured Light Scanning Sensor Structure Parameter Integration[J]., 2014, 27(9): 1197-1120.
[5] 陈新禹, 马孜, 陈天飞. 线结构光传感器模型的简易标定[J]. 光学精密工程, 2012, 20(11): 2347-2350.
CHEN Xin-yu, MA Zi, CHEN Tian-fei. Calibration model for Line Structured Light Vision Sensor[J]., 2012, 20(11): 2347-2350.
[6] 裘祖荣, 陈培芬, 李杏华. 多线结构光视觉传感器测量系统的标定[J]. 半导体光电, 2014, 35(5): 890-893.
QIU Zu-rong, CHEN Pei-fen, LI Xing-hua. Calibration of Measurement System for Multi-Vision Sensor[J]., 2014, 35(5): 890-893.
[7] 王向军, 王晶, 刘峰, 等. 野外大视场双目视觉物体定位监测系统的单参数快速标定[J]. 光学精密工程, 2013, 21(10): 2665-2667.
WANG Xiang-jun, WANG Jing, LIU Feng, et al. Fast Calibration for Binocularvision measuring system with a large field[J]., 2013, 21(10): 2665-2667.
[8] 张晓龙, 刘英, 孙强. 高精度非致冷长波红外热像仪的辐射标定[J]. 中国光学, 2012, 5(3): 235-241
ZHANG Xiao-long, LIU Ying, SUN Qiang. Radiometric calibration of uncooled long-wave infrared thermal imager with high-precision[J]., 2012, 5(3): 235-241.
Fast Calibration Method of Multiple Line Structured Light and the Camera
CHEN Wenliang,DONG Qingliang,LIU Feng,WANG Xiangjun,WU Fanlu
(,,300072,)
In order to realize fast calibration of the line structured light in the stereo vision, a calibration method for multiple line structured light of monocular vision measurement was proposed. In this method, the internal camera parameters were determined based on Zhenyou Zhang’s camera calibration. And the extrinsic camera parameters can be got by using the three-dimensional arraycolumn target. The rotation matrix and the translation matrix were got when the center points of the upright columns of the three-dimensional array target and the pixel coordinates were known; after the line structured light projects on the head face of the upright columns, the relation between the object and the image can be got, and then the plane equation can be fitted. After that, the relation between the line structured light and the camera would begot, then the calibration was finished. Experimental results indicate that itsrelative error is about 0.57%.
three-dimensional array column target,line structured light,calibration of camera,plane equation
TP391
A
1001-8891(2017)01-0081-05
2015-09-09;
2017-01-12.
陈文亮(1977-),男,副教授,研究方向:应用光谱。
