数学教学中问题情境创设的探索
2017-03-27曹剑基
曹剑基

(广东省清远市清城区源潭镇第一初级中学)
摘 要:数学问题情境是学生掌握知识、形成能力、培养创新意识、发展心理品质的重要源泉。在中学数学教学中,教师应根据教学大纲,从学生实际出发,创设具有趣味性、生活化而又合理的问题情境,激发学生学习的兴趣,让学生主动、愉快地开展探究学习;形成数学意识;提高学生的创新能力和实践能力。
关键词:问题情境;创设方式;有效合理;兴趣;探究
所谓问题情境指的是一种具有一定困难,需要努力克服(寻求达到目标的途径),而又是力所能及的学习情境(学习任务)。实践证明,创设有效合理的问题情境可以激活学生的求知欲;形成数学意识;诱发出学生自我解决问题的动力。以下谈谈笔者的做法和体会:
一、设法创设适宜的问题情境,促使学生主动学习
1.创设趣味性的问题情境,激发学生的求知欲望
苏霍姆林斯基说过:“课上得幽默有趣,学生可以带着一种高涨的、激动的情绪从事学习和思考。并对前面展示的真理感到惊奇和震惊。”实践证明,精心设计一些新颖“奇特”富有趣味的问题,能调动学生学习的积极性和主动性,让学生乐于开展探究学习。例如,在学习“一元一次方程的应用”时,我引入以下故事:希腊数学家丢番图的墓碑上记载着:“他生命的1/6是幸福的童年;再活了他生命的1/12,两颊长起了细细的胡须;又度过了一生的1/7,他结婚了;再过5年,他有了儿子,感到很幸福;可是儿子只活了他全部年龄的一半;儿子死后,他在极度痛苦中度过了4年,与世长辞了。”(1)他去世时的年龄是多少?(2)他结婚时的年龄是多少?创设这样的故事问题情境能马上引起学生对故事的好奇,激发学习的兴趣。使学生主动、愉快地参与探究,从而巩固所学知识,培养学生的思维能力,同时也培养了学生应用数学知识解决实际问题的意识。
2.创设生活化的问题情境,增强数学意识
从学生喜闻乐见的生活情境出发,使抽象的数学学习变得具体形象起来,把原来枯燥的、脱离学生生活实际的数学变得生动起来。把问题情境生活化,就是把问题情境与学生的生活紧密联系起来,让学生亲自体验问题情境中的问题,增加学生的直接经验,这不但有利于学生理解问题情境中的数学问题,而且有利于使学生体验到生活中的数学是无处不在的,从而培养学生的观察能力和初步解决实际问题的能力。例如,在学习用数学式子表示变量关系时,我创设了以下问题情境:清远市家庭电话月租费为18元,市内通话费平均每次0.2元。(1)若小珊家上个月共打出市内电话x次,那么,上个月小珊家应付费y与x之间的关系是什么?(2)按如此收费标准,若你家上个月共打出市内电话100次,那么你家应付费多少元?对于这种生活中经常碰到的问题,一下子就激发学生的兴趣。经过思考,发现生活中的问题可以转化为数学问题来解决,提高学生应用数学知识的能力和增强学生的数学意识。
3.问题情境设在“最近发展区”,诱发出学生自我解决问题的动力
在数学教学中,教师要研究学生的知识能力水平,深入细致地钻研教材。所创设的问题难度要与量力性一致的原则。要善于从与新知识相联系的旧知识中找准新知识的生长点,把学生引进旧知识的“最近发展区”,启用旧知识去获取新知识。例如,在学习“整式的加减”一课时,计算(7a2+2a+b)-(3a2+2a-b),教师先提出问题:(7a2+2a+b)和(3a2+2a-b)去括号后得到什么?对于这样熟悉的问题学生很快便得出结果: 7a2+2a+b和-3a2-2a+b。这时教师再提出问题: 7a2-3a2= ,2a-2a= ,b+b= 。对于合并同类项的知识也是学生所熟悉的,学生会主动、积极、迅速地算出来。然后,教师再归纳整式加减的步骤:①去括号;②合并同类项。这样的问题情境设计刚好落在学生的 “最近发展区”内,诱发出学生自我解决问题的动力,让学生积极主动地从旧知识中获取新知识。
二、问题情境的创设还要注意以下几点
1.问题情境的创设要具有探索性
布鲁纳说过:“探索是数学的生命线。”因此,教师要创设有探索性的问题情境,以疑点燃学生的思维火花,从而引导学生在问题的导引下主动探究、获取知识、增长能力。这是培养创造性思维的有效途径。例如,某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
上述问题中,第五排、第六排分别有多少个座位?第n排有多少个座位?你是如何得到的,并与同伴进行交流。于是学生便通过观察、猜想、概括,从而找出规律。经过这些探索过程能点燃学生的思维,增长能力,培养学生的创造性思维。
2.问题情境的创设要具有挑战性
挑战性的问题,就是让学生感觉到问题很熟悉,学生运用已有的知识和经验又无法解决,学生必须重新建构自己的知识结构。例如,在学习“线段的中垂线性质”一课时,我设计以下题目:
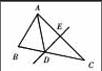
如图,在△ABC中,DE是AC的垂直平分线,AE=3,①若AC=BC,求BC;②若△ABD的周长为13,求△ABC的周长。
对于第一个问题学生依据中线的定义很快便求出BC=6。当解第二个问题时,学生觉得求△ABC的周长这个问题很熟悉。但经过思考且与同伴交流,还是不能解决。于是出现认知冲突下产生学习的需要的情况,激发学生的求知欲。这时,教师便引入中垂线性质,使学生不仅在探索中获取新知识,还能提高运用数学知识解决实际问题的能力,发展创新意识。
3.问题情境的创设要具有开放性
开放性的问题就是指问题的条件、结论或过程开放。在数学教学中创设开放性问题能巩固和深化学生所学知识,使学生养成独立思考、勇于探索的习惯;也为学生探索能力的发展提供了广阔的空间。例如,有一道习题:有四根细木棒,长度分别为4 cm、7 cm、10 cm、13 cm,哪三根木棒可以组成一个三角形?有几种可能的情况?说明你的理由。于是学生通过思考、实验得出了三种可能的情况,分别为4 cm、7 cm、10 cm,7 cm、10 cm、13 cm,4 cm、10 cm、13 cm。通过这类题目的训练,培养了学生思维的发散性,提高思维的灵活性、多向性、选择性,使学生的潜能得到充分发挥。
以上仅是本人在教学中创设问题情境的点滴体会。总之,在数学课堂教学中,我们要想方设法创设适宜的问题情境,激发学生的学习动机,促使学生去主动探究。最终培养学生思维的形成与解决问题能力。
参考文献:
[1]章建跃.关于课堂教学中设置问题情境的几个问题[J].数学通报,1994(6).
[2]肖柏荣.数学教育设计的艺术[J].數学通报,1996(10).
[3]潘莉霞.初中数学课堂问题情境的创设研究[D].南京师范大学,2007.
[4]李俊红.数学教学情境创设的理论与实践探索[D].云南师范大学,2005.
编辑 温雪莲