巧设问题，构建生本课堂

叶雪芬

《数学课程标准》指出：教学活动是师生积极参与、交往互动、共同发展的过程。学生是学习的主体，教师是学习的组织者、引导者和参与者。课程改革也需要教师改变观念，努力做到“以生为本，以学定教”。那么，教师在课堂上的提问就要站在学生的角度，根据学生的生活经验和已有知识，巧妙地设计出问题。

一、乱花渐欲迷人眼——迷失教学本真

《圆的面积》这节课的其中一个教学目标是通过操作，引导学生推导出圆面积的计算公式，并能运用公式解答一些简单的实际问题。对于六年级的学生来说，利用公式解答问题是比较简单的，难点在于圆面积公式的推导。我听到学校同级段一位老教师是这样上的：

【片段】

师：请同学们回忆长方形、正方形、平行四边形、三角形面积公式的推导？

生：（略）

师：那圆的面积该怎么算呢？

生：转化成学过的图形进行计算。

师：请你把圆分成16等份，剪开后，用这些近似于等腰三角形的小纸片拼成近似的平行四边形。

师：如果把圆分成32份，剪拼后，又会是什么图形呢？

师：下面请同学们仔细观察、分析这个近似的长方形与圆的关系，小组讨论并思考以下几个问题：

（1）圆的面积与这个长方形的面积有什么关系？

（2）这个长方形的长与圆的周长有什么关系？

（3）这个长方形的宽与圆的半径有什么关系？

（学生在教师的引导下推导出了圆的面积）

以前，自己也曾上过这节课，教学模式与执教老师类似。这样的教学，教师引导的太多，学生自主发挥的不够。学生完全是在教师的要求下把圆剪拼成平行四边形的，又是在教师的引导下推导出圆的面积的。课堂成了教师一个人的舞台，没有学生的巧妙构思，也没有学生的独立思考，其他一切都显得苍白无力。意识到这一点后，我思索着如何改变这一现状。如果放手让学生自己去拼的话，学生应该可以根据自己的想法拼出更丰富的图形，也应该可以通过小组合作、交流、讨论，推导出圆的面积。

二、柳暗花明又一村——打破思维的定势

看来，学生学习的方向由教师的提问决定。提问得当，不仅能吸引学生，更能提高教学的效率，也能保证教学的质量和效果。那么，教师在课堂上该如何站在学生的角度设计问题呢？是否可以让学生的思维更发散些呢？我在本课教学时做了以下调整：

【片段】

师：还记得平行四边形、三角形、梯形的面积是怎么推导的吗？

生：（略）

师：说一说：这些图形面积公式的推导过程都什么共同点？

生：都是把它转化成已经学过的图形来推导。

师：那圆面积又该怎么计算呢？

生：可以像其他平面图形一样，转换成学过的图形来推导公式。

师：如何转化？

生：可以把圆分成若干（偶数）等份，剪开后，拼一拼。

师：四人小组合作，试着剪一剪、拼一拼。

（学生小组合作，拼出了近似的三角形、梯形和平行四边形。）

投影展示学生作品：

生：把圆平均分的份数越多，每一份就会越细，拼成的图形就会越来越像个长方形。

师：那这个剪拼后的长方形面积与圆面积有什么关系呢？你能算出这个近似长方形的面积吗？同桌合作说一说、算一算。

三、拨云见日总有时——构建生本的课堂

《数学课程标准》中指出：数学教育要面向全体学生，要适应学生个性发展的需要，使得人人在数学上得到充分发展，不同的人在数学上得到不同的发展。在本节课中，我注重问题的设计，设计出指向性、启发性、开放性、挑战性的问题，能够使知识点横向联系，纵向深入，串点成线，聚线成面，既有利于提高课堂效率，又有利于激发学生思维，提高学生思维能力，有利于学生通过数学问题把握数学本质。

1.设计指向性问题，引导学生的学习

教师设计教学问题要有明确的目标和方向，即为引起新课、为训练重点、为突破难点、为总结归纳。只有明确了问题设计的目的性和指向性，才能使问题恰到好处，为教学穿针引线，收到较好的教学效果。

例如：《圆的面积》教学时，教师可以在复习其他平面图形的面积推导过程后，设计这样一个问题：“圆的面积公式的的图形呢？”通过这个问题，让学生迅速回忆学过的知识，调动原有的知识储备，为新知的“再创造”做好知识的准备。通过这个问题，学生也明确接下来要做的事就是把圆转化成其他学过的平面图形，沟通两者之间的联系，从而推导出圆的面积公式。

2.设计启发性问题，诱发学生的思考

启发性是指教师所设计的教学问题要能触动学生思维，给学生正确的思维方法及方向。切忌设计一些“是不是” “对不对”之类比较简单的问题，这些问题只能让学生厌烦，对培养学生思维能力不利。

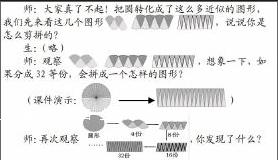
例如在教学《圆的面积》时，学生通过动手操作把若干等份的扇形拼出近似平行四边形后，想象把圆分成32等份，会拼成一个怎样的图形？然后再通过课件的演示，拼成一个近似的长方形。最后让学生观察从4等份的圆至32等份的圆

拼成的图形，提问：通过观察这些图形

开放性问题是数学教学一种模式，是教师提问的一个方向，具有新颖性、发散性和创新性等特点，还具有一定的知识教育价值、能力发展教育价值和人文教育价值，可以引导学生多方面思考问题，发散学生的思维。

当学生通过预习，已经知道要把圆转化成学过的平面图形后，教师可以提问：“你想把圆剪拼成什么平面图形呢？”此时，学生便能随着自己的想法，拼成想拼的平面图形。四人小组交流汇报时，有的学生能拼出近似的平行四边

4.设计挑战性问题，提高学生的能力

每个学生都是一座等待开发的宝藏，只要教师善于吊足学生的“胃口”，触碰他们内心的“小宇宙”，给他们创造挑战自我的契机，学生会给你惊喜。课堂上，教师若能根据学生的学情，设计富有挑战性的问题，有利于激发学生的兴趣，充分调动组织原有的知识经验解决问题。

作为教师，我们要创设符合学生认知规律的问题情境， 大胆巧妙地设计问题，吸引学生产生浓厚兴趣，层层深入，以问促思，由思而探，使學生在积极思维活动中体验获得成功的喜悦，激发学习兴趣，挖掘学生的内在潜能，使他们的思维在课堂上自由驰骋，从而生成课堂的无限精彩。