在课堂互动中丰富计算教学的探索
2017-03-25李日炎
李日炎

改变计算教学活动枯燥、沉闷的局面,营造主动、宽松、活跃的课堂氛围,以丰富的活动内容为载体,引导学生经历探索算法、理解算理的过程,引发学生的数学思考,提高学生的运算能力,是计算教学探索的热点问题。《义务教育数学课程标准(2011年版)》指出:教学活动需要师生进行积极的沟通交流,是一种相互启发、相互补充的过程。在计算教学活动中实施课堂互动,引导学生激活探究所需的经验,引导学生围绕问题的核心进行深度探索、思想碰撞等,可实现师生在教学活动中分享彼此的经验、知识和思考,交流彼此的观念、体验和情感,丰富教学活动过程,共同发展。
由同课异构课例引发的思考
2016年,笔者参加了茂名市一次教研活动,其中,高州市第二小学崔文浩老师、茂名市第六小学赖海燕老师作了北师大版四年级上册数学《卫星运行时间》(三位数乘两位数)同课异构课例展示。两位老师的课体现了教师鼓励学生自主探索、培养学生的实践能力。下面谈谈笔者的听课体会:
崔文浩老师创设了和谐的师生关系,课堂互动起伏有效。他改变教材的呈现方式,以读书、购书为主题创设问题情境,融入三位数乘两位数的运算教学。在指导学生理解算理、探索算法的过程中,开展“想一想”“估一估”“算一算”“说一说”等活动。
赖海燕老师的课例设计紧扣教材,运用取近似值、估算等知识作为学习新课的基础,启发学生应用估算,体验精确值与准确值运算过程的联系与区别。他们以学生为主体,放手让学生自主学习,探索、交流、操作等,获得一定的教学效果。
笔者认为以上教学课例存在的问题及努力方向有:①教学活动的设计,未能根据学生已有的知识和经验组织开展计算教学,体验计算的乐趣与价值;②未有效利用课堂的动态生成资源引导学生探索算法、算理;③教学过程各环节时间安排欠合理,教师讲得多些,学生表达、对话的机会少;④指导学生用列表法运算时,对表内各项数的运算算理分析、理解欠深刻;⑤在指导学生探索三位数乘两位数竖式算法上,对列表法及竖式算法的内在联系把握欠准确,对算理的理解不够透切。
在课堂互动中丰富计算教学
基于以上课例的思考,笔者在丰富计算教学的内容与形式上作了以下探索:
一是规范学生的数学语言,培养数学交流素养,促进对算理的理解。科学的数学语言是指利用数学的符号、表格和图表合理交流的能力,分析数学表格和图表的能力。学生在课堂规范使用数学语言表达身边的数学现象,结合学习活动表达自己的思维过程和数学见解,反思并修正自己的数学观点,可促进对数学的理解。学生在交流中学习数学,并运用数学语言中特定的符号、词汇和句法去交流,去认识世界,从而获得知识、方法和经验的积累。例题一:在教学三位乘两位数算法时,用列表法进行探索算法算理的环节,可让学生先讨论表中两个因数分解的各个位值的含义,经历数的分解、运算、合并等变化过程,并说出上述活动过程并及时进行相应的训练。如:出现因数114,立即想到按位值分解为100、10、4;反之,出现位值100、10、4时,即想到因数114,并准确地表达出来。表中的计算结果出现2000、200、80时,能按位值制合并后说出是2280。例题二:一种图书每套售价114元,如果一个班有30人,每人买1套,一共需要多少元?在此可借助课堂生成资源,讨论计算114×30的策略:①先算3套书的钱,再算30套书的钱数(114×3×10);②先算10套书的价钱,再算30套书的价钱(114×10×3)……通过以上互动讨论,为学习三位数乘两位数的竖式算法积累了知识与经验。
二是紧扣教材,研究学情,弄清学生学习新课应具备的基础知识和基本活动经验。教材中,本单元是小学阶段整数乘法运算的最后一个内容。在这之前,学生已经积累了表内乘法和两(三)位数乘一位数以及两位数乘两位数口算与笔算的经验,具备了一定的运算能力。从表内乘法到三位数乘两位数,由于位数的增加及数范围的扩大,计算过程越复杂,大约需要10步乘法和加法口算才能完成一次正确的笔算,此类乘法计算具有一定的难度。因此,结合教材的具体情境,引入估算,积累用估算法解题的经验,培养估算意识。同时,应用位值的知识及整十数、整百数、简单的两(三)位数乘一位数的口算或笔算,探索计算策略的多样化,具有重要的实践意义。例题三:我国发射的第一颗人造地球卫星绕地球1圈需要114分。算一算,绕地球21圈需要多少时间?说说你是怎样算的?探索算法策略过程,其主要算法如下:
上例激活了学生已有三位数乘一位数、整十整百数相乘的口算或笔算的经验,探索和体会如何把两位数乘两位数的算法与算理迁移到三位数乘两位数的情形。
三是把握教学内容的重点,指导学生在探索知识的形成过程展开讨论与思考、互动交流。本节课学习应以列表法与竖式计算作为重点学习的内容。列表法的算理是什么?应如何引导学生掌握算理、算法?在计算方法的探索上,笔者认为,列表法表中将乘数分项计算内涵是:根据计数的位置制,三位数分解为三个位值,两位数分为两个位值,因数1与因数2的位值互相乘一次,共相乘得6个积,这6个积合并起来的和就是三位数乘两位数的积(如例题三)。在教学活动引导学生分析竖式计算的各步骤,其运算原理与前面的列表法是完全一致的,实质也是运用位值原理步步相乘,再相加的过程。理解竖式中的每一步相乘结果对齐乘数的哪一位的原理也是教学要着力解决的难点。如例题三④:十位的“2”(表示20)与另一乘数十位的“1”(表示10)相乘得“2”,该结果“2”表示200,所以竖式算得该结果“2”对齐乘数的百位;有进位的向前一位进位。最后让学生弄清竖式计算过程实质是列表法的简便表现形式,两者是一脉相承的,探索活动绝不能忽视这两种方法的本质联系。笔者想在教学中学生能理解到这一层次,对学生的运算能力将有更大的促进作用。
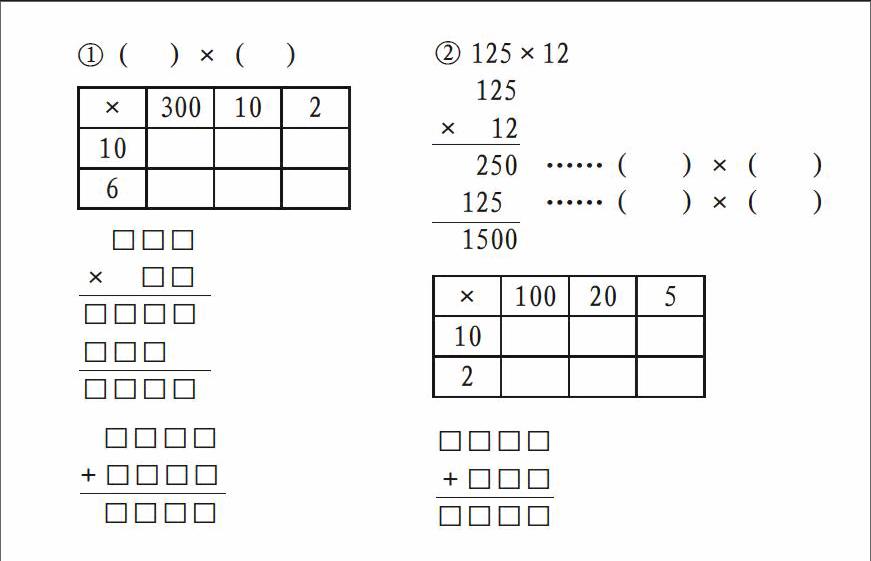
四是设计有针对性的练习,做有价值的训练。为巩固新知识,结合教学内容的重点和难点,设计一些有针对性的口头练习、书面练习。如可创设一些问题情境,让学生讨论算法、理解算理,就列表法与竖式算法的联系设计一些填空等练习。例题四:想一想,填一填。
以上习题能对探索三位数乘兩位数竖式计算方法的过程进行有效的巩固。此外,还可以列举一些纠正错误的题型让学生观察、分析,并在课堂互动中理解算理,掌握竖式算法。
结束语
通过上述的思考与实践,数学教师需在学生计算的基础知识水平及经验、计算的基本技巧、计算方法的探索过程、课堂的训练等方面,努力探究丰富计算教学活动的有效做法。结合现实问题,在课堂互动中放手让学生经历计算方法的探索过程,在与他人交流算法的过程中,学会表达自己的想法,逐步养成善于倾听、敢于质疑、敏于思考的好习惯。只要不断坚持这样的实践,必将有助于提高学生的运算能力,有助于发展学生的核心素养,有助于成就学生的数学发展。
参考文献
[1]王光明,范文贵.新版课程标准解析与教学指导:小学数学[M].北京:北京师范大学出版社,2012.
[2]王永春.小学数学与数学思想方法[M].上海:华东师范大学出版社,2014.
[3]中小学数学课程教材改革与发展研究[M].广州:广东高等教育出版社,2016.
[4]叶立军.数学教师课堂教学行为研究[M].杭州:浙江大学出版社,2014.
【本文系广东省教育科学“十二五”规划课题《构建小学数学互动课堂的研究》(课题批准号2015YQJK212)成果】
(作者单位:广东省茂名市茂南区教育局教研室)
