运动学问题中的高效解题方法归纳

兰军亮

摘 要：众所周知，同一道物理问题往往有多种不同的解题方法，选择最合适的解题方法可以减少运算量，加快解题速度，特别是在广东高考采用全国卷、题目难度加大的背景下，如何训练学生采用更简单的方法解决问题，已成为高中物理教师必须要思考的问题。归纳总结了高中物理运动学问题中的三种比较高效的解题方法，即：临界状态法、极限思维法、逆向思维法。

关键词：运动学；临界状态法；极限思维法；逆向思维法

一、选择合适的解题方法

在日常教学中我们经常会碰到这样的学生，他们一拿到题目就低头猛算，试图用自己最惯常的办法解决这道题目，但是常常事与愿违，算到焦头烂额、满头大汗都解决不了问题，所以就跑来问老师。如果这位学生不试着掌握新的方法，而是一再重复原有的方法去解决问题，那么即便这位学生把这种方法重复一千次，他的水平也不会有很大的提高。只有当这位学生开始试着思考用何种方法解决这道题目更简便的时候，他的学习才会产生质的变化。

不同的物理情景需要采用不同的解题方法，例如，当题目中出现要求某个物理量的取值范围时，就应当用临界状态法解决问题；当处理匀减速运动时，一般用逆向思维法解决问题会更简单；当处理涉及多个运动物体的追击问题时，用图象法解决问题，清楚又明白；当处理变加速问题时，将其合理地与我们熟悉的简单运动进行类比分析，会大大加快我们解题的速度。

二、运动学问题中的高效解题策略

1.临界状态法

在解决运动学问题时要善于利用一些特殊状态寻找突破口，有一类最常用的特殊状态就是临界状态。临界状态是指在运动过程中物体的运动状态发生改变的瞬间所处的状态。利用物体的临界状态作为分析问题、解决问题的思维起点是一种非常有效的思考途径，这种方法称为临界状态法。

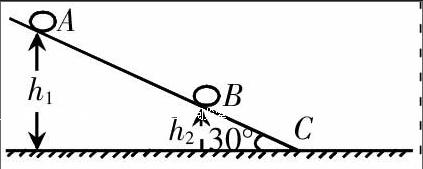
例1：如图所示，倾角为30°的足够长光滑斜面下端与一足够长光滑水平面相接，连接处用一光滑小圆弧过渡，斜面上距水平面高度分别为h1=20 m和h2=5 m的两点上，各静置一小球A和B。某时刻由静止开始释放A球，经过一段时间t后，再由静止开始释放B球。g取10 m/s2，求：

（1）为了保证A、B两球不会在斜面上相碰，t最长不能超过多少？

（2）若A球从斜面上h1高度处自由下滑的同时，B球受到恒定外力作用从C点以加速度a由静止开始向右运动，则加速度a满足什么条件时A球能追上B球？

思路分析：第一问求t最长不能超过多少，第二问求加速度a的取值范围，这些都是采用临界状态法解题的标志性语言。第一问是在满足A、B两球不会在斜面上相碰这一条件下，t最长不能超过多少，那么这个问题的临界状态是什么呢？临界状态应该是两球恰能在c点相遇，如果t再大一点，就在斜面上相遇，如果t再小一点，就在平面上相遇了。

第二问求速度a满足什么条件时A球能追上B球，这个问题的临界状态是什么呢？B球的加速度取最大值时，两球恰好在速度相等时相遇了，B球的加速度再大一点点A就不能追上B。凡是求某个物理的量可能的取值，或是最大值，最小值诸如此类的问题，就要培养学生能够把问题细化到某一个具体的临界状态的情景中，只有这样才能写出方程，解出取值范围。

2.极限思维法

极限思维法是高中阶段常用的高效解题方法之一，特别是在处理选择题时，往往使用极限思维法能够迅速快捷地找出答案，甚至于在处理一些计算题的时候，用极限思维法可以迅速确定大概的运动过程和大致的物理情景。在使用极限思维法解题时，一定要先判定物理量间的变化关系是否为单调变化，如果物理量间的变化关系为单调变化，则就可以假设某个物理量的极端情况，从而得出结论或作出判断。

例2：如图所示，用轻绳通过定滑轮牵引小船靠岸，若收绳的速度为V1，则在绳与水平方向夹角为θ的时刻，船的速度v有多大？（阻力不计）。

思路分析：假設小船在Δt时间内从A点移过Δs到C点，这时出现了三个距离：小船前进的位移Δs，绳收缩的距离Δs1以及Δs2，这个运动可设想为两个分运动所合成：小船先被绳拉过Δs1到B点，再随绳绕滑轮O点做圆周运动到C点，位移为s2。若Δt很小，Δθ→O，即Δs1与Δs2垂直，此时有Δs1=Δscosθ，可得：Δs1/Δt=Δscosθ/Δt，则V1=vcosθ。

3.逆向思维法

在运动学中，逆向思维法多用于处理匀减速运动的某些问题，因为匀减速运动的逆过程是初速度为零的匀加速运动，而初速度为零的匀加速运动解决起来是比较容易的，但是如果是用常规解法按照匀减速运动来处理，步骤往往比较多，而且容易出错。

例3：一小物体以一定的初速度自光滑斜面的底端a点上滑，最远可达b点，e为ab的中点，已知物体由a到e的时间为t0，则它从e经b再返回e所需时间为（ ）

A.t0 B.（-1）t0

C.2（+1）t0 D.（2+1）t0

思路分析：由逆向思维可知物体从b到e和从e到a的时间比为：1：（-1）；即：t：t0=1：（-1），得t=（+1）t0，由运动的对称性可得从e到b和从b到e的时间相等，所以从e经b再返回e所需时间为2t，即2（+1）t0。

参考文献：

[1]潘志荣.论高中物理教学中解题能力的培养[J].华夏教师，2015（2）：84.

[2]豆平祖.高中物理教学中学生解题能力的培养思路刍议[J].才智，2015（22）：135.