基于学生探究活动的关键性问题研究

洪细苗

[摘 要] 以学生的探究活动为着准点，提炼了“三角形的面积”这一课的关键性问题，并基于这些关键性问题进行教学设计，着重引导学生通过三角形的面积计算方法的推导去理解和掌握三角形的面积计算公式，并能运用三角形的面积计算公式计算相关图形的面积，从而解决实际问题。

[关键词]关键性问题；探究活动；三角形的面积

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）08-0031-02

【教学背景】

1.基于教材分析而产生的困惑

“三角形的面积”是人教版数学五年级上册第六单元第二课时的教学内容。本节课是在学生用数方格比较图形的面积，认识三角形的底和高，掌握长方形、正方形、平行四边形的面积计算方法及推导平行四边形面积公式的基础上进行教学的。同时，它与平行四边形、梯形的面积联系在一起，为学生以后学习组合图形的面积和圆的面积计算公式做好铺垫。本节课主要引导学生通过三角形面积计算方法的推导去理解和掌握三角形面积计算公式，并使学生能运用三角形的面积计算公式计算相关图形的面积，从而解决实际问题。

对此，笔者有这样的困惑：学生在学习长方形、正方形和平行四边形的面积时，都没有事先准备两个完全一样的图形的经验，为什么学习三角形的面积，事先要做这样的准备？这是学生自身学习的需要，还是教师教学的需要？这样的教学是对学生真实学情的顺应，还是教材编排和教师设计意图的强加？有没有更好的方法来启发学生主动构想三角形的“另一半”呢？

2.基于困惑提炼关键性问题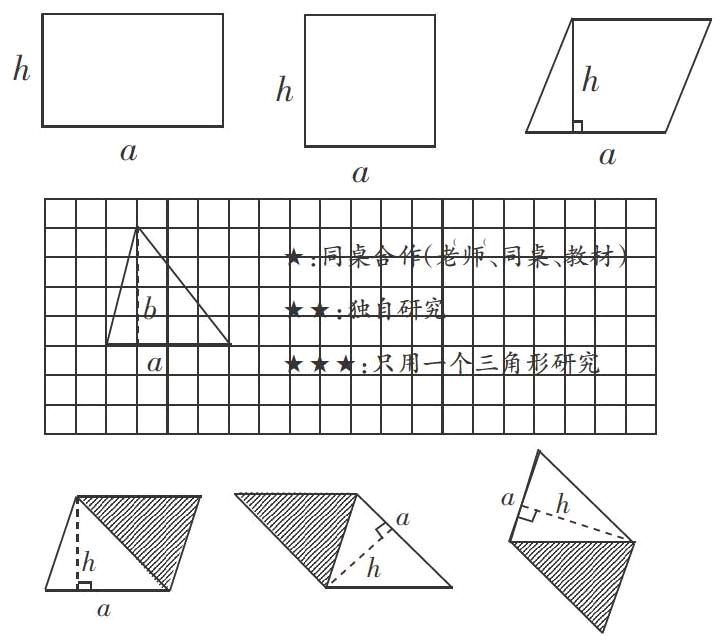

基于上述困惑，笔者以学生的探究活动为着准点，提炼了以下关键性问题。

问题1：如何基于方格图，只用一个三角形来研究三角形面积的计算方法？

问题2：如何采用一个锐角三角形，通过三次不同的拼法，证明三角形面积计算公式的完备性？

为了解决这两个关键性问题，笔者设计了如下的教学设计流程。

【教学设计】

1.复习引入

（1）说一说我们都学习了哪些图形面积的公式？

（2）平行四边形面积公式的推广。

师：如果把这些图形都看成是底和高，那么它们的面积可以怎么算？

（3）联想：今天我们要学习三角形的面积，你能联想到什么？

2.自主探究

（1）再次呈现长方形、正方形和平行四边形，提问：你看到三角形的影子了吗？

（2）计算：（把长方形、正方形和平行四边形都分成两个完全一样的三角形，出示底和高）你会求三角形的面积吗？现在你知道三角形的面积公式了吗？

（3）猜想：请你猜一猜，三角形的面积可能怎么推导？

（4）公式推导：老师只给你准备一个三角形，有什么办法推导？

（5）自主探究：只选其中一个三角形进行研究，转化成以前学过的图形，根据提示，同桌说说三角形的面积计算公式怎么推导。

（6）反馈评价：①为什么要除以2？②有没有不一样的推导方法？

（7）质疑：如果换另外一条底和高，能不能推导出三角形的面积计算公式呢？

（8）提升：只能用一个三角形，能不能通过剪拼来转化，从而推导出三角形的面积计算公式？

（9）结合学生汇报，通过几何画板让学生感悟等积变形的推导方法。

（10）公式推广：同学们，这么多种方法，你最容易想到什么办法？下面这些图形你能联想到可以拼成什么图形来推导吗？在直角三角形、钝角三角形中能不能适用呢？再让学生运用公式计算面积。

3.练习提升

（1）拓展提升：如果要用5作为底来求三角形的面积，还缺少什么条件？请你猜测一下高大概是多少？

（2）再次感悟同一个三角形中不同的底×高除以2都能求出三角形的面积：老师告诉你，高是2.4，你有什么发现？

（3）巩固“等底等高的三角形面积相等”的理解：我们再来看这个三角形，（几何画板拉动三角形）现在什么变了，什么不变？你又有什么新的发现？

4.全课总结（略）

【课后反思】

结合关键性问题，笔者力求让学生以长方形和平行四边形的面积计算为基础，以图形内在联系为线索，以未知转化为已知的基本方法开展三角形面积计算方法的学习，使学生经历“提出问题——大胆猜想——学习验证——拓展延伸”的数学学习过程，从三个层次对两个关键性问题进行破解。

第一层次：二度思维铺垫。

铺垫一：上过这节课的教师都会有这样感觉：学生们在“从未知图形到已知图形转化”的探究后，反馈交流时经常会“宽”“高”不分，导致思路混乱、阐述不清，容易对结论的得出产生很大的干扰。而其实长方形、正方形都是一种特殊的平行四边形，因此在课始我们先给学生第一层思维铺垫，在这里把长方形的长、宽和正方形的边长统一成平行四边形的底和高。而且为了让学生能更有效地反馈自己的转化过程，笔者还在“实验操作单”上给学生提供有利于他们汇报操作过程的模版（如下圖）。

铺垫二：平行四边形的面积推导是对三角形面积推导的一种负迁移。面对平行四边形中的“割补”转化的负迁移，笔者设计了“从长方形、正方形和平行四边形的身上找到三角形的影子”这一探究活动，让学生们从平行四边形中找到三角形，建立平行四边形与三角形的联系。基于这一活动实现从平行四边形到三角形的转化，同时也避免了“等积”转化这一思维定式，为接下来的三角形面积计算公式推导中的“倍增”转化设下思维铺垫。

也就是说，通过这一系列的思维铺垫，在破解关键性问题1“如何基于方格图，只用一个三角形来研究面积的计算方法”时，我们是成功了一小步，让全班大多数学生都能有效地进行探究，包括在思维上比较弱势，比较后进的那小部分学生，也能有效地参与到课堂探究中，不再只做课堂的旁观者。

第二层次：公式推导的深入挖掘。

“三角形面积计算公式”自主探究中最难的一个环节，就是用“割补”的方法运用“等积”转化来推导三角形的面积计算公式。我们在课堂实践中大约10位学生挑战了这种转化方法，我们就主要通过以下两点预设让这些学生能成功地突破本堂课的学习难点。

（1）为学生提供了格子图，降低了“割补”的难度。

（2）通过前面的铺垫，学生已经明确三角形的面积计算公式为S=ah÷2，这一面积计算公式为学生的思考提供了方向。

第二层次的“挖”，不仅突破了本堂课的学习难点，同时也增强了学生的探究兴趣，提高学生的推理能力，促进学生对问题深层思考，形成良好的思维习惯。有了这样的思维习惯，我们就能在以后的学习道路上“邂逅”智慧。

当然，为了让这种探究活动不再是个别学生的“独角戏”，笔者还用几何画板将这一过程清晰地展示在学生面前。在刚才的课堂中可以听到很多学生在看到这一演示过程时，都发出了惊叹声。这一声声惊叹，不就是一种“顿悟”的证明吗？！

第三层次： 公式完备性证明。

只用一个锐角三角形就得出三角形面积计算公式，显然有以点概面之嫌。如何从锐角三角形这个“点”出发，到所有的三角形这个“面”，從而证明三角形面积计算公式的完备性？通过以下两个方面此问题可以得以解决。

在探究的第一层次中，也就是通过找完全相同的三角形来实现从三角形到平行四边形的“倍增”转化中，我们不停留在一组底和高，而是让学生感知不同的三组底和高都能得出三角形面积计算的公式，从而第一次证明了三角形面积计算公式的完备性。而第二次就是在练习中实现从锐角三角形到钝角三角形再到直角三角形。练习中，第一个计算锐角三角形的面积是对S=ah÷2的一种巩固练习，而在第二次计算钝角三角形的面积时，笔者借助课件给学生演示了转化成平行四边形的过程，正是从锐角三角形到钝角三角形的一种推广，一种从点到面的过程，而直角三角形中除了这相同的推广外，还设计一组底和高来求面积，而另一组只知“底”不知“高”。而这求高的过程，正是一种提升。从巩固到推广再到提升，学生与美丽的智慧正“邂逅”于此。

（责编 黄春香）