分析高职考试真题分类突破知识要点

摘要：本文首先分析了职高学生数学学习的现状，论述了高职考试对于高职学生的重要性，笔者以一元二次函数的复习为例，统计了2011年——2016年的高职考试真题中关于“三个二次”的考查分布，然后对相关的题型进行了分类整理，设计了“一元二次函数的应用”的学案，并对高职考试复习进行了三点反思.

关键词：考试真题；分类突破

作者简介：邓丹 （1983-），女 ，本科 ，中学一级 ，主要从事职高数学教学研究一、职高学生数学学习的现状

众所周知，职高学生的数学基础薄弱，对数学有种莫名其妙的恐惧心理，觉得数学很难学，看到一大串数字就像看天书，你看着我，我看着你，好像“执手相看泪眼，竟无语凝噎” ，学生数学学习苦、累；同时，常常看到我们职高老师教的辛苦，不理解学生怎么这么简单都不懂，课堂上都讲了n遍了，还是不会啊，依葫芦画了还不像“瓢”，那个痛苦啊，只有老师自己心里最清楚，“想说爱你真不是一件很容易的事”.总结起来，职高学生数学学习有如下特征：

（1）基础薄弱，连基本的计算都不过关；

（2）基础知识混乱，例如一元二次方程和一元二次函数分不清楚，有些学生一看到“函数”二字就头疼，不敢下手；

（3）对于实际应用题，无法读懂题意，无法提取有用的信息.

二、高职考试对于高职学生的重要性

高职考试对每一个考生来说，都非常重要，关系到每个学生的升学问题和专业的选择.

既然职高学生的基础薄弱，高职考试对他们又如此重要，那么作为一线的高三教师，我们该如何进行高职考试的数学复习呢？复习该遵循什么原则和要求呢？

三、高职考试复习的总体原则和要求

1.高职考试的总体复习原则是——“三个理解”

“三个理解”即 “理解数学、理解学生、理解教学”的原则，深入理解数学是前提，“理解数学”是数学课堂教学“预设”的前提，也是數学课堂教学“生成”的关键.作为教师，只有清晰地知道“教什么”，理解所教内容“是什么”，深知数学知识所蕴含的思想方法和自身的科学价值，才有可能在课堂教学中予以表达.学生是课堂教学的主体，“理解学生”就是要解决“教给谁”的问题.在课堂教学中，教师将已经“理解”的数学知识，要传授给学生，那么，就一定要知道学生在“这个问题”上“已经知道了什么”；在将要学习的内容中，可能遇到的思维障碍是什么；以及对于“这个问题”，是如何展开“思考”的.教学过程，应该是以数学知识发生发展过程为载体的学生的认知过程.基于教师对课堂教学中的载体“数学知识”的理解，对教学对象“学生认知”的理解，接下来，就是要解决“途径”的问题，即讨论“怎样教”，才能使学生获得最大的学习效益.

2.高职考试的总体复习要求

根据《浙江省高等职业技术教育招生数学考试大纲（2013年修订）》，高等职业学校招生数学考试，以人民教育出版社、高等教育出版社出版的《数学》教材为参考教材.数学考试旨在测试中学数学基础知识、基本方法、基本技能、运算能力、逻辑思维能力、空间想象能力，以及运用所学数学知识和方法，分析问题和解决问题的能力.本大纲对所列知识提出三个不同层次的要求，三个层次由低到高顺序排列，且高一级层次要求包含低一级层次要求.三个层次分别为：

了解：要求学生对学过知识进行复述和辨认，对所列知识的涵义有感性和初步理性的认识，知道有关内容，并能进行直接运用.

理解：要求学生对所列知识涵义有理性的认识，能在了解知识基本内容的基础上作相应的解释、举例或变形、推断，并能运用知识解决简单的数学问题.

掌握：要求学生对所列知识在理解基础上，能综合运用有关知识，解决一些数学问题和简单实际问题.

四、分析高职考试真题、分类突破知识要点

1.对比考试大纲，详细分析近五年高职考试真题

比如不等式部分，考试大纲中要求，会解一元一次不等式，一元一次不等式组和可化为一元一次不等式组的不等式；会解一元二次不等式，了解区间的概念.会在数轴上表示不等式或不等式组的解集，那么在历年的高职考试真题中有哪些体现？是以什么题型出现的？每个题目的难易程度如何？在相应的课堂教学中，我们该如何进行有效突破这些知识要点？

比如函数部分，考试大纲中要求，理解一元二次函数的概念，掌握它们的图像与性质，了解一元二次函数、一元二次方程、一元二次不等式之间的关系，会求一元二次函数的解析式及最大、最小值，能初步联系实际建立一元二次函数模型，会运用一元二次函数的知识解决一些简单的实际问题，那么在近些年的高职考试真题中，哪些题目涉及到一元二次函数、一元二次方程、一元二次不等式，是以什么样的题型出现？每个题目的分值、难易程度如何？这些问题在我们教学之前，都必须思考清楚，也是我们进行职高复习设计的原则“三个理解”的体现，即理解数学的重要体现.

2.分类突破知识要点

分类突破知识要点的方法很多，一般来说，可以根据知识点来进行分类突破，也可以按题型来进行突破，有时也会按专题进行分类突破，形式不一，但是针对性要强，即在“理解学生”的基础上，首先进行点对点进行突破，然后进行思维提升，变式训练等.

五、以“一元二次函数复习”为例进行分析、分类突破知识要点

1.分析高职考试题

分析2011年——2016年浙江省高职考试数学试卷，可以得出，“三个二次”（即一元二次函数、一元二次方程、一元二次不等式）在试卷中所占的比例很大，从下面统计的表格可以清楚看出.

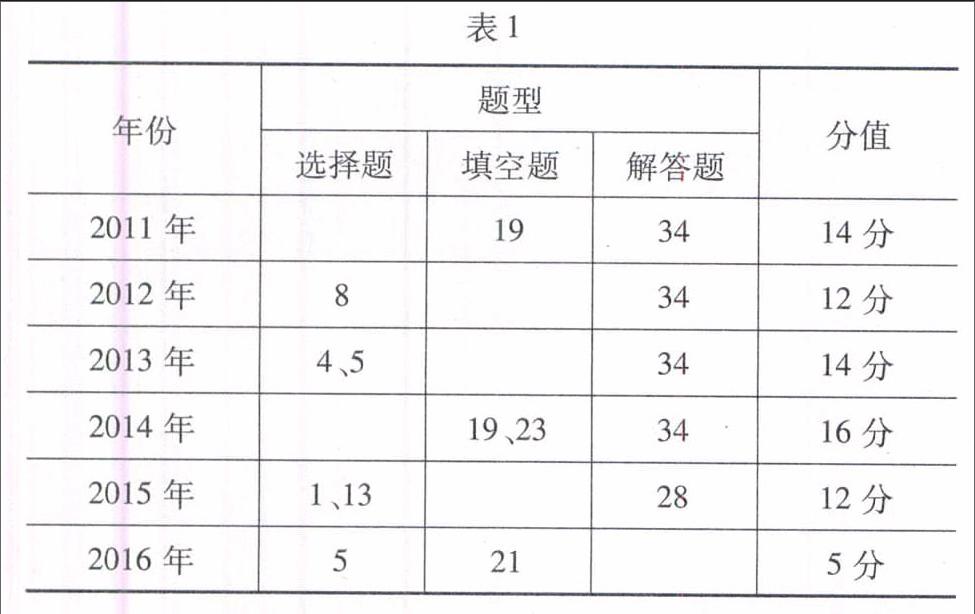
2011年—2016年浙江省高职考试数学试卷“三个二次”题型分布表

表1

年份题型选择题填空题解答题分值2011年193414分2012年83412分2013年4、53414分2014年19、233416分2015年1、132812分2016年5215分在上述表格中，对“三个二次”的考查，表现在如下方面：理解一元二次函数的概念，掌握它们的图像与性质，了解一元二次函数、一元二次方程、一元二次不等式之间的关系，会求一元二次函数的解析式及最大、最小值，能初步联系实际建立一元二次函数模型，会运用一元二次函数的知识解决一些简单的实际问题.这与考试大纲的要求是吻合的.

2.分类突破知识要点

知识点一：一元二次方程的解

例1（2016年浙江省高等职业技术教育招生考试数学试卷）若函数f（x）=x2-6x，则

A.f（6）+f（8）=f（10）B.f（6）+f（8）=2f（7）

C.f（6）+f（8）=f（14）D.f（6）+f（8）=f（-2）

例2（2015年浙江省高等职业技术教育招生考试数学试卷）已知集合M={x|x2+x+3=0}，则下列结论正确的是（）

A.集合M中共有2个元素

B.集合M中共有2个相同元素

C.集合M中共有1个元素

D.集合M为空集

例3（2012年浙江省高等职业技术教育招生考试数学试卷）设p：x=3，q：x2-2x-3=0，则下面表述正确的是（）

A.p是q的充分条件，但p不是q的必要条件

B.p是q的必要条件，但p不是q的充分条件

C.p是q的充要条件

D.p既不是q的充分条件也不是q的必要条件

知识点二：一元二次函数的图像和计算

例4（2014年浙江省高等职业技术教育招生考试 数学试卷）已知二次函数的图象通过点（0，-1），（1，12），（-1，-72）则该函数图象的对称轴方程为.

例5（2014年浙江省高等职业技术教育招生考试 数学试卷）函数f（x）=-2x2+5x+3图象的顶点坐标是

例6（2013年浙江省高等职业技术教育招生考试 数学试卷）对于二次函数y=x2-2x-3，下述结论中不正确的是（）

A. 开口向上

B.对称轴为x=1

C.与x轴有两交点

D.在區间（-∞，1）上单调递增

例7（2015年浙江省高等职业技术教育招生考试数学试卷）已知函数f（x）=x2-1

3-2x x≥0

x<0，求值：

（1）f（-12）； （2）f（2-0.5）；（3）f（t-1）；

知识点三：一元二次函数的最值问题

例8（2014年浙江省高等职业技术教育招生考试数学试卷）若0

例9（2011年浙江省高等职业技术教育招生考试数学试卷）0

例10（2015年浙江省高等职业技术教育招生考试数学试卷）二次函数f（x）=ax2+4x-3的最大值为5，则f（3）=（）

A.2B.-2 C.92D.-92

知识点四：一元二次不等式

例11（2013年浙江省高等职业技术教育招生考试 数学试卷）函数f（x）=x2-4的定义域为（）

A.（2，+∞） B.[2，+∞）C.（-∞，-2]∪[2，+∞）D.实数集R

知识点五：一元二次函数的应用题

例12（2014年浙江省高等职业技术教育招生考试 数学试卷）两边靠墙的一个区域，边界正好是椭圆轨迹的一部分，如图所示，现要设计一个长方形花坛，要求其不靠墙的顶点正好落在椭圆轨迹上，

（1）根据所给条件，求出椭圆的标准方程

（2）求长方形的面积S与边长x的函数关系式

（3）求当边长x为多少时，面积S有最大值，并求其最大值

例13（2013年浙江省高等职业技术教育招生考试 数学试卷）有60（m）长的钢材，要制作一个如图所示的窗框.

（1）求窗框面积y（m2）与窗框宽x（m）的函数关系式；

（2）求窗框宽x（m）为多少时，窗框面积y（m2）有最大值；

（3）求窗框的最大面积.

例14（2012年浙江省高等职业技术教育招生考试 数学试卷）有400米长的篱笆材料，如果利用已有的一面墙（设长度够用）作为一边，围成一个矩形菜地，如图，设矩形菜地的宽为x米.

（1）求矩形菜地面积y与矩形菜地宽z之间的函数关系式；

（2）当矩形菜地宽为多少时，矩形菜地面积取得最大值？菜地的最大面积为多少？

例15（2011年浙江省高等职业技术教育招生考试 数学试卷） （如图所示）计划用12m长的塑钢材料构建一个窗框.求：

（1）窗框面积y与窗框长度x之间的函数关系式；

（2）窗框长取多少时，能使窗框的采光面积最大；

（3）窗框的最大采光面积.

六、突破一元二次函数的知识点——“一元二次函数的应用”的复习学案

根据上述关于2011年—2016年高职考试数学试卷“三个二次”的分析，笔者针对“一元二次函数的应用”这一知识点进行分类突破，设计了一元二次函数的应用学案，供同行参考.

一元二次函数的应用（学案）

课堂练习：

1.（2011高职变式题）用12m长的塑钢材料建一个窗框（如图所示），求（1）面积y与x的函数关系式（2）当窗框宽为多少时，采光面积最大？

2.（2012高职）有400米长的篱笆材料，如果利用已有的一面墙（设长度够用）作为一边，围成一个矩形菜地，如图，设矩形菜地的宽为x米.（1）求矩形菜地面积y与矩形菜地宽x之间的函数关系式；（2）当矩形菜地宽为多少时，矩形菜地面积取得最大值？菜地的最大面积为多少？

3.（利润变式题）某职业中学市场营销专业二年级学生李明利用暑假时间做了一次生意，她用20元/件的价格从市场批发了某种品牌精美饰品1000件，然后在自家淘宝家店销售，下表是4天销售情况.她发现在25元基础上，每提价1元销量就减少1件.问：结合数学知识，如何定价才能使日利润最大？

价格25元26元27元28元销量15件14件13件12件课后巩固提高：

练习1：有400米长的篱笆材料，如果利用已有的两面墙（设长度够用）作为两边，围成一个矩形菜地，如图，设矩形菜地的长为x米.（1）求面积y与x之间的函数关系式；（2）当长为多少时，面积最大？

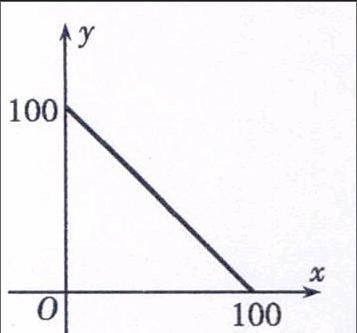
练习2：某商品的进价为30元/件，试销期间商品定价x元/件与销量y（元）存在的函数关系式的图像如图所示.

（1）求销售量y与定价x的函数关系式；

（2）当定价为多少时，商品的利润最大？并求最大利润.

练习3：在某块地上种葡萄藤，若种50株葡萄藤，每株葡萄藤将产出70千克葡萄，若多种1株葡萄藤，每株产量平均下降1千克，试问在这块地上种多少株葡萄藤才能使产量达到最大，并求出最大值.

练习4：如下图，AB=10，BC=5，在矩形ABCD上分别选取E、F、G、H四点，且AE=AH=CF=CG=t，如何設计，可使EFGH面积最大？

练习5：某小店销售某种商品，已知平均月销售量x（件）与货价p（元/件）之间的函数关系式为p=120-x，销售x件商品的成本函数为C=500+30x，试讨论：（1）该店平均月销售量为多少时，所得利润不少于1500？（2）当平均月销售量x为何值时，能获得最大利润？并求出最大利润.

七、高职考试复习的几点反思

1.知识点落实到位

高职考试的难度和普高考试的难度不同，比较起普高的高考考试题目来说，相对简单，但是高职考试题量大，对于基础薄弱、运算能力较差的职高学生来说，存在很大的挑战，因此，在高职考试复习过程中，我们选题时题目尽量简单点，不要求进行深入探究，但是选题时一定要根据知识点选题，落实到位，训练到位，使得学生熟能生巧.

2.分类突破知识要点

对于历年的高职考试真题必须足够的重视，命题的专家一般变化不大，命题的思路和趋势必然有延续性，不会出现非常大的变化，让大家感到不适应，因此，分类整理历年的高职考试真题就显得尤为重要，分析清楚了这些真题，心里就清楚命题专家的命题方向和思路、题型等，在复习的过程中就做到心中有“题”，讲“题”不慌，分类整理，突破知识要点，复习的效率也会提升.

3.利用变式进行提升

分析、分类整理清楚历年高职考试的真题，对于个别较难的知识点，学生不太容易掌握的知识点，比如一元二次函数的应用问题，既是学生头疼的问题，也是历年高职考试的重点，所占的分值较大，所以我们在复习的时候，常常利用变式进行提升，专题巩固突破比较有效.

参考文献：

[1]章建跃. 中学数学课改的十个论题[J].中学数学教学参考.2010年（7）.

[2][美]波利亚. 怎样解题[M].北京：科学出版社，1982.

[3]罗增儒.数学解题学引论[M].陕西：陕西师范大学出版社.2008年.

[4]浙江省高等职业技术教育招生数学考试大纲（2013年修订），2013年.