创设连贯性问题情境教学案例

杨志杰

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2017）04-0118-02

问题教学的渊源可以先后追溯到古希腊苏格拉底的“对话式”辩论、近代美国杜威的“通过解决问题进行学习”的思想。而在实际教学中，可以引导学生在完成实践性作业时创设问题情境。

在数学教学中，有的问题情境具有一定的连贯性，可以组成一个问题系列，出现在问题系列中的问题应按数学知识的发生发展过程，以相应的数学思想和数学方法为主线，组成一个循序渐进的、具有内在联系的问题体系，在这一体系中，开始提出的问题是基本的、贯穿教学过程的，它应能引起学生对掌握知识的迫切需要，随后的一系列具体问题都要为继续揭示新知识的本质规律服务，这些具体问题应能帮助学生循序渐进地掌握开始时提出问题中包含的那些新知识。

待定系数法这一节的教学，通过具体实例中的连贯性问题，一步一步引导学生提出，进而寻求解决问题的方法，以下是这一节课总体设计：

一、教学设计

1.教学目标：掌握用待定系数法求函数的解析式的方法；会根据所给信息用待定系数法求一次函数解析式，发展解决问题的能力；通过自主、合作学习，培养学生勇于探索、勤于思考的精神。

2.教学构思：函数是初中数学的重要内容，也是初中数学教学的难点。这节课通过引入3道求正、反比例函数及一次函数解析式的练习，然后通过教师的一步一步创设情境题目，引导学生讨论，逐步从中概括出共同的解题步骤，进而揭示出待定系数法的含义，接着让学生演练了3道由浅入深用待定系数法求函数解析式的题目，对待定系数法这个数学方法进行集中训练。

二、教学过程

教师引入问题情境：我们已经学过了正比例函数、反比例函数、一次函数的定义，图像及性质，也学习了求正、反比例函数及一次函数的解析式，现在请大家来做几道练习。

1.若正比例函数图像经过点（1，2），求此函数的解析式。

2.反比例函数图像如图所示，求此反比例函数的解析式。

3.一次函数图像经过点（1，5）及（-1，1）两点，求此一次函数的解析式。三位同学同时板演：

生1：解设y=kx（k≠0）

因为图像经过点（1，2），所以2=k×1，解得k=2，所以y=2x

生2：解设y=k＼x（k≠0）

因为图像经过点（1，-2），

所以-2=k×1，解得k=-2，所以y=-2＼x

生3：解设kx+b（k≠0）

因为图像经过点（1，5）和（-1，1）

所以5=k+b，1=-k+b，解得k=3，b=2，所以y=-3x+2

师：请同学们检查上述三位同学的正、误。生：对的。

师：请同学们讨论一下上述三道题目的解题过程有何共同之处？

生：第一步是设解析式。

师：这些解析式中k，b是已知吗？生：未知。

师：我们把它们叫作未知系数，那么这些解析式就是含有未知系数的解析式。第二步呢？生：第二步是根据条件，把数字代入解析式。

师：我们所代入的式子，分别称它们为什么？生：方程、方程组。

师：这就是根据条件列出的方程、方程组。第三步呢？

生：解方程、方程组，求出k，b的值。

师：出示小结。步骤：

1.设出含有未知系数的表达式；

2.根据条件列出方程（组）；

3.通过解方程（组）确定未知系数。

我们把上面这样的解题方法叫作待定系数法。

出示课题：“待定系数法”

师：现在我们已经懂得了什么是待定系数法及待定系数法的解题步骤，下面我们继续用待定系数法来解几道题。

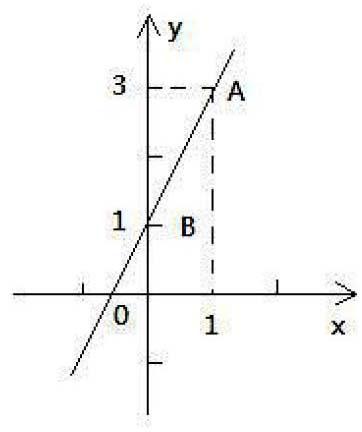
1.一次函数图像如图，求此解析式。

师：利用待定系数法，可以怎样来解这道题呢？

生：可以设定解析式后，把A（1，3），B（0，1）两点代入，然后解方程，得出k，b的值。

师：有其它的解法吗？

生：有。由图像可以知道b=1，在把点A（1，3）代入即可。

师：我们在设未知数时，应该根据条件，尽量减少未知数的个数，这样可以简化解题过程。

2.反比例函数的图像经过点（2，3），求此反比例函数的解析式。（解略）

3.一次函数与正比例函数y=-x图像平行，且与反比例函数图像都经过点A（1，5），求：（1）反比例函数的解析式；

（2）一次函数的解析式。

生板演：（1）解：设反比例函数的解析式为y=k＼x（k≠0），代入点（1，5）得5=k＼1，解得k=5，所以y=5＼x

（2）解设一次函数的解析式为y=kx+b（k≠0），

因为图像平行于y=-x，所以k=-1，

把点A（1，5）代入得5=-1+b，解得b=6

所以一次函數的解析式为y=-x+6

师：一个题目中，同时出现两个解析式，应该将加以区分，设，y=k1＼x（k1≠0），y=k2x+b（k2≠0）

又因为，直线y=k2x+b与y=-x平行，这就暗示了 k2=-1。

生：可设y=-x+b，减少一个未知系数。

师：刚才用待定系数法解题时，都要先设出含有未知系数的解析式，否则难以用待定系数法解题。

师：同学们已经初步掌握待定系数法的解题步骤和方法。待定系数法是数学中的常用方法之一，待定系数法可用于求代数式，方程和函数解析式。随着同学们的知识不断丰富，待定系数法使用的范围会不断扩大，希望大家在今后的学习中，进一步掌握好待定系数法。

三、教学反思

本节课中，首先让学生做3道求正、反比例函数及一次函数解析式的练习，引导学生讨论，逐步从中概括出共同的解题步骤，进而揭示出待定系数法的含义，接着让学生演练了3道由浅入深用待定系数法求函数解析式的题目。使学生深化理解，对待定系数法这个数学方法进行集中训练，为今后的应用打下一个较好的基础。

在整个教学过程 ，学生的学习过程就是一个不断发现问题、分析问题再去认识更高层次问题的过程。“情境”对学习过程来说，有着至关重要的引导作用，以情境为中心，围绕科学的并能激发学生思维的“情境”展开学习，也是科学探究学习的重要特征。情境的创设，可以随着教学过程的开展成为一个连续的过程，从而使教学氛围形成一个又一个高潮。因此在课堂教学中努力创设恰当的情境，通过情境启发学生积极地观察、思维。以“情境”为主线 来组织和调控课堂教学，能充分调动学生学习的主体性，促进学生科学探究活动的开展和探究能力的培养。

参考文献：

[1]郭岗田.数学教学方法与策略，黑龙江教育出版社，2006.5

[2]朱成杰.数学思想方法教学研究导论，文滙出版社，1998.6