蝴蝶定理在仿射几何中的推广

黄一德，田秀蓉

（华南农业大学 数学与信息学院，广东 广州 510642）

蝴蝶定理在仿射几何中的推广

黄一德，田秀蓉

（华南农业大学 数学与信息学院，广东 广州 510642）

历史上关于蝴蝶定理的各种推广和证明,纷繁复杂.本文试图整理出蝴蝶定理在保留中点的情况下,在仿射几何中最好的推广方式,并给出综合法的证明.本文得到的主要结果是定理1,2,3,这三条定理可以包扩蝴蝶定理在仿射几何领域的各种推广.最后通过定理4验证了上述结果.

蝴蝶定理；Desargues第2定理；仿射几何

1 引言

蝴蝶定理自从1803年被提出,直到现在依然可以看到有关蝴蝶定理的论文发表.例如从1986年到2016年,国内的期刊上主题是关于蝴蝶定理的论文,我们找到的就有110篇,而出现的有关证明也是数不胜数.真有点让人不知要领.《大学》说：“止于至善.”那么蝴蝶定理的至善推广和证明应该是什么呢?本文试图整理出蝴蝶定理在保留中点的情况下,在仿射几何中最好推广方式,并给出综合法的证明.

2 欧氏几何中的蝴蝶定理

蝴蝶定理最早提出的时候是一个欧氏几何定理,可以叙述如下.

蝴蝶定理经过一个圆的弦CC'的中点A作另外两条弦ST和UV.直线CC'分别交直线SU,TV于点B,B'.那么A是B,B'的中点[1].

如果需要在蝴蝶定理中保留中点这个概念,那么在欧氏几何中,应该没必要再讨论蝴蝶定理的各种推广了,也没有必要在欧氏几何中找蝴蝶定理的最反映问题本质的证明,因为把蝴蝶定理的圆改为椭圆,双曲线或抛物线,定理依然成立,而且证明并不需要涉及度量概念 (距离,角度等).例如1892年,John Casey用交比证明了蝴蝶定理[1].但如果不保留中点这个概念,蝴蝶定理还是有一些有意义的推广的,例如A.Kandy的推广[1].

3 蝴蝶定理在仿射几何中的推广

因为中点是一个仿射不变量,所以如果需要在蝴蝶定理中保留中点这个概念,我们应该在仿射几何中推广蝴蝶定理.本文的仿射几何指的是实仿射几何.我们知道,常常可以借助射影几何研究仿射几何,我们研究蝴蝶定理的工具就是Desargues第二定理.

Desargues第二定理设直线l与一个二阶曲线束S相交,且l不过S的任一基点,则与S的每一条二阶曲线的一对交点都属于同一个对合[2].

按照基点为4个,退化为3个和退化为2个,可以把Desargues第二定理分别叙述为三个定理, 见[3]第五章定理19,20,21.

为了在仿射几何中推广蝴蝶定理并给出综合法的证明,我们先证明一个引理.

引理设l是一条平常直线,N是l上的无穷远点,σ是l上点列的一个对合.

(1)如果无穷远点N是σ的一个二重点,那么σ在上的限制是关于另一个二重点M的反射.

(2)如果σ有两个相异的平常的共轭点对,它们有相同的中点M,那么σ在l-{N}上的限制是关于点M的反射.

说明如果一个对合有一个二重元素,那么它有另一个不同于前者的二重元素([3]第四章定理27推论4).

证明(1)设A,A'是σ的一对平常的共轭点,那么它们与M,N构成调和共轭点对([3]第四章定理27推论1).因为N是无穷远点,所以M是A,A'的中点.因此σ在l-{N}上的限制是关于点M的反射.

(2)设A,A'和B,B'是两个相异的平常的共轭点对,它们有相同的中点M.令σ'是一个l上点列的对合,使得M和N是二重点(σ'是存在的,见[3]第四章定理27推论2).根据(1), σ'在l-{N}上的限制是关于点M的反射.因为σ和σ'在A,B上的作用相同,所以([3]第四章定理26推论).证毕.

定理1(仿射几何中的蝴蝶定理) 令S,T,U,V是四个平常点,其中任意三点不共线.设三条互异的二阶曲线经过这四个公共点.又令不经过这四个点的一条平常直线l与这三条二阶曲线的三对交点分别是A,A',B,B',C,C'.于是如果有一对交点的两个点都是直线l上的无穷远点,那么另外两对交点有相同中点.如果三对交点的点都是平常点,并且其中两对交点有相同中点,那么这个点也是另外一对交点的中点.

说明(1)显然,三对交点的集合{A,A'},{B,B'},{C,C'}互不相交.

(2)l与一条非退化二阶曲线的两个交点重合,相当于说l与这条非退化二阶曲线相切于这个交点.

(3)如果三对交点都是平常点,并且其中一对交点重合,例如,如果A=A',那么定理的结论就相当于说,A是B,B'的中点等价于A是C,C'的中点.

(4)如果定理1所说的一条二阶曲线是退化的,那么它是完全四点形STUV的一对对边.

(5)如果定理1所说的一条二阶曲线与l的两个交点都是无穷远点,那么或者这条二阶曲线是完全四点形STUV的一对对边,并且这对对边平行于l,或者这条二阶曲线是双曲线,它的一条渐近线是l.

图1画的是这三条二阶曲线有两条退化,一条非退化时的示意图.

图1

证明根据[3]第五章定理19,这三对交点是同一个对合的三对共轭点.如果A,A'都是直线l上的无穷远点,那么B,B',C,C;都是直线l上的平常点,根据引理的(1),B,B'的中点与C,C'的中点相同.如果三对交点的点都是平常点,并且A, A'与B,B'有相同的中点,那么根据引理的(2),这个点也是C, C'的中点.证毕.

定理1中的四个点可以退化为三个点,这时定理按如下方式理解.

定理2(定理1的退化情形1)令T,U,V是不共线三个平常点,t是经过点T但不经过U,V的直线.设三条互异的二阶曲线属于下列情形：与直线相切于T,并经过U和V的非退化二阶曲线,或直线对t,UV,或直线对TU,TV.又令不经过T,U,V的一条平常直线l与这三条二阶曲线的三对交点分别是A,A',B,B',C,C'.于是如果有一对交点的两个点都是直线l上的无穷远点,那么另外两对交点有相同中点.如果三对交点的点都是平常点,并且其中两对交点有相同中点,那么这个点也是另外一对交点的中点.

说明如果定理2所说的一条二阶曲线与l的两个交点都是无穷远点,那么或者这条二阶曲线是直线对t,UV,并且t,UV平行于,或者这条二阶曲线是双曲线,它的一条渐近线是l.

图2画的是这三条二阶曲线有两条退化,一条非退化时的示意图.

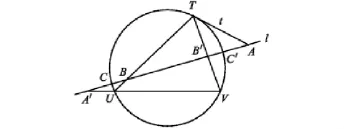
图2

证明根据[3]第五章定理20,这三对交点是同一个对合的三对共轭点.证明的其余部分可参考定理1的证明.证毕.

定理1中的四个点还可以退化为两个点,这时定理按如下方式理解.

定理3(定理1的退化情形2)令T,V是两个不同的平常点,t是经过T但不经过V的直线,v是经过V但不经过T的直线.设三条互异的二阶曲线属于下列情形：t与直线v和 分别相切于点T和V的非退化二阶曲线,或直线对t,v,或重合直线对TV.又令不经过T,V的一条平常直线l与这三条二阶曲线的三对交点分别是A,A',B,B',C,C'.于是如果有一对交点的两个点都是直线l上的无穷远点,那么另外两对交点有相同中点.如果三对交点的点都是平常点,并且其中两对交点有相同中点,那么这个点也是另外一对交点的中点.

说明如果定理3所说的一条二阶曲线与l的两个交点都是无穷远点,那么或者这条二阶曲线是直线对s,t,并且s,t平行于l,或者这条二阶曲线是重合直线对ST,并且ST平行于 ,或者这条二阶曲线是双曲线,它的一条渐近线是.

图3画的是这三条二阶曲线有两条退化,一条非退化时的示意图.

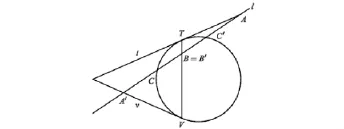
图3

证明根据[3]第五章定理21,这三对交点是同一个对合的三对共轭点.证明的其余部分可参考定理1的证明.证毕.

定理1,2,3可以包扩蝴蝶定理在仿射几何的各种推广.

4 应用举例

根据定理1,2,3,在仿射平面上很容易得出不少蝴蝶定理的特例.我们举一个稍微复杂一点的例子.

定理4设CC'DD'是平常的简单四点形,S,T,U,V分别是直线CD,C'D',CD',C'D上的平常点,其中任意三点不共线, {C'C'D'D'}和{S,T,U,V}不相交,并且四条直线CC',DD',ST,UV相交于点A.又令直线CC'与直线SU,TV的交点分别是B, B'.于是A是B,B'的中点等价于A是C,C'的中点.

证明显然CSTC'VU是一个简单六点形,它的三对对边的交点分别是D,A,D',而这三个点在一直线上,根据Pascal定理的逆定理,六点形CSTC'VU内接于一条二阶曲线.于是直线CC'与这条二阶曲线以及直线对ST,UV,直线对SU,TV的三对交点分别是C,C',A,A,B,B'.根据定理1,A是B,B'的中点等价于A是C,C'的中点.证毕.

在定理4中,如果把简单四点形CC'DD'改为筝形,那么定理4就变为1990年全国数学冬令营竞赛的一道试题.这样一改,定理4就从仿射几何问题变为欧氏几何问题,因为筝形是欧氏几何的概念.

〔1〕L.Bankoff.The Metamorphosis of the Butterfly Problem[J].Mathematics Magazine,1987,60(4)：195-210.

〔2〕钟集.高等几何[M].北京：高等教育出版社,1983.3.

〔3〕O.VeblenandJ.W.Young.Projective Geometry, Volume 1[M].Charleston：Biblio Bazaar,2009.

O185

A

1673-260X（2017）02-0004-02

2016-10-27