高等数学中不等式证明的几类常用方法
2017-03-23潘娟娟凌雪岷
潘娟娟,凌雪岷
(安徽新华学院 通识教育部,安徽 合肥 230088)
高等数学中不等式证明的几类常用方法
潘娟娟,凌雪岷
(安徽新华学院 通识教育部,安徽 合肥 230088)
不等式在高等数学中的应用非常广泛,但是其本身逻辑性较强,证明方法多样,学习难度较大.本文立足高等数学,通过实例补充介绍了6种比较常用的证明不等式的方法,对每种方法给出了具体的证明思路,并辅以典型例题,旨在使学生对不等式的证明有更深的理解和掌握.
高等数学;不等式;证明
不等式的证明是高等数学中重要的考察内容,正确的使用不等式可以将一些复杂的数学问题简单化,但是不等式证明方法多样且繁杂,学生在使用时往往无法选择最合适且最简便的方法,因此对不等式证明方法进行总结和归纳很有必要,既可以提高教师的教学水平,还可以增强学生学习的效果.基于不等式的重要性,本文总结了证明不等式的几种常用的方法,并配以具体的例子,便于学生更好的掌握不等式证明的技巧,在以后的学习中可以熟练的选择合适的简洁的证明方法.
1 利用函数的性质证明不等式
1.1 函数的凹凸性
定义1[1]设f(x)在区间I上连续,如果对任意两点x1,x2恒有
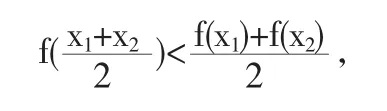
那么称f(x)在I上的图像是(向上)凹的(或凹弧);
如果恒有
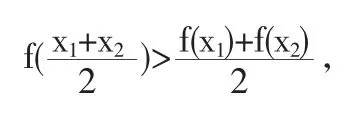
那么称f(x)在I上的图像是(向上)凸的(或凸弧).

说明 函数判定函数的凹凸性,一般我们不通过定义去判定,而是通过凹凸性的判定定理来判定,设f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数,那么若在(a,b)内f"(x)>0 (或f"(x)<0),则f(x)在[a,b]上图形是凹(或凸)的[1].
1.2 函数的单调性
利用函数的单调性比较函数的大小,是高等数学不等式证明中常用到的方法之一.

说明 利用函数单调性证明不等式的一般步骤:
(1)构造辅助函数f(x);
(2)根据f'(x)的符号判定函数的单调性;
(3)根据函数f(x)的单调性,得出所求不等式.
2 利用Lagrange中值定理和Cauchy中值定理证明不等式
2.1 Lagrange中值定理[1]
如果函数f(x)满足:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导,那么在(a,b)内至少有一点ξ (a<ξ<b),使等式

成立.
例3 设b<a<0,证明nan-1(b-a)<bn-an<nbn-1(b-a).
证 设f(x)=xn,显然f(x)在区间[a,b]上满足拉格朗日中值定理的条件,根据定理,应有f(b)-f(a)=f'(ξ)(b-a)(a<ξ<b),由于f'(ξ)=nξn-1,因此上式可化简为bn-an=nξn-1(b-a),又由于a<ξ<b,有nan-1(b-a)<nξn-1(b-a)<nbn-1(b-a),
即nan-1(b-a)<bn-an<nbn-1(b-a).
说明 利用Lagrange中值定理证明不等式的步骤如下:
(1)通过观察不等式经过恒等变形可以化成函数值之差的形式,则可考虑运用拉格朗日中值定理,并合理设定f(x);
(2)根据a<ξ<b对拉格朗日中值定理进行适当的放缩,推导出所证不等式.
2.2 Cauchy中值定理[1]
如果函数f(x)及F(x)满足:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;
(3)对任一x∈(a,b),F'(x)≠0,
那么在(a,b)内至少有一点ξ(a<ξ<b)使不等式

成立.
例4 设e<a<b<e2.证明


3 利用Taylor公式证明不等式
高等数学中,泰勒公式除了用于逼近一些较复杂的的函数、近似值计算以及求函数极限以外,还可以用于证明一些几何不等式.
例5 b>a>e证明:ab>ba.

说明 运用泰勒展开具体步骤如下:
(1)合理给出辅助函数f(x),给出函数在某点的泰勒展开式,展开式的阶数根据具体题设来确定;
(2)根据所证不等式,对朗格朗日余项进行适当的放缩,从而证明出所给不等式.
4 利用函数的最值证明不等式
利用闭区间上连续函数的有界性与最大值最小值定理,求出函数f(x)在区间的最大值M和最小值m,则该函数在区间段内任意值都满足f(x)≤M或者f(x)≥m.

5 利用定积分的性质证明不等式
5.1 定积分的估值定理[2]
设M及m分别是函数f(x)在区间[a,b]上的最大值和最小值,则
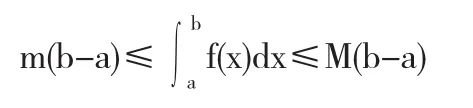
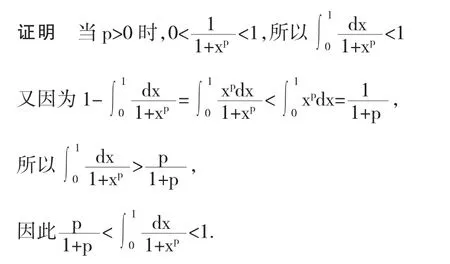
说明 找出被积函数的在积分区间上的最大值和最小值,可以估计积分值的大致范围,从而证明了不等式.
5.2 积分中值定理[1]
如果函数f(x)在区间[a,b]上连续,至少存在一个点ξ,使下式成立:
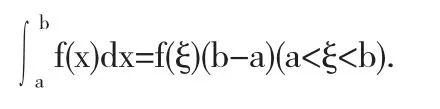
积分中值定理是解决含有积分不等式问题的重要方式之一.
例8 设f(x)在[0,1]连续单调减,

6 利用定积分中的一些著名不等式证明不等式
柯西-施瓦茨不等式

例9 设f(x)在区间[a,b]上连续,且f(x)>0.证明:



说明 利用琴生不等式证明不等式时,要选用合适的辅助函数,然后通过求一阶二阶导数得到函数的凹凸性,根据琴生不等式求证.
8 结语
本文仅仅总结归纳了高等数学中七种常用的证明不等式的方法,但是教学过程中并不仅仅局限于上述若干种方法,而且同一个问题也可以选择不同的证明方法去解决,这就需要教师和数学爱好者在平时的教学工作中不断去发觉和探索,从而可以综合运用各种方法和技巧灵活解决不等式证明的相关问题.
〔1〕同济大学数学系.高等数学[M].北京:高等教育出版社,2015.
〔2〕裴礼文.数学分析中的典型问题和方法[M].北京:高等教育出版社,2001.
O172
A
1673-260X(2017)02-0001-03
2016-09-02
安徽省高校省级重点项目(KJ2016A310);安徽省级质量工程项目名师工作室(2014msgzs168)
