蒙特卡洛法评定在线pH计示值误差的不确定度

周宁宁，孙倩芸，刘继义，高捷，李芬，赵道林

（山东省计量科学研究院，济南 250014）

蒙特卡洛法评定在线pH计示值误差的不确定度

周宁宁，孙倩芸，刘继义，高捷，李芬，赵道林

（山东省计量科学研究院，济南 250014）

以在线pH计为例，考察了在线酸度计示值误差不确定度的分布规律，利用蒙特卡洛法评定示值误差不确定度。对于0.01级的在线pH计，蒙特卡洛法与GUM法评定结果的差值为9.1%，小于不可靠性（20%）；对于0.1级的在线pH计，蒙特卡洛法与GUM法评定结果的差值为3.8%，小于不可靠性（10%）。通过比较得出结论，采用GUM 法验证了蒙特卡洛法（MCM）根据JJF 1547-2015评定在线pH计示值误差不确定度的方法是有效且适用的。尤其在测量模型非线性以及输出量的概率密度函数（PDF）较大程度地偏离正态分布或t分布等GUM法不适用的场合，蒙特卡洛法是评定在线分析监测仪器仪表示值误差不确定度的重要手段。

在线分析监测；在线pH计；GUM法；蒙特卡洛法；验证

近年来，由于具有安装使用方便、抗干扰能力强、维护量小等方面的优点，工业在线分析监测仪器仪表广泛地应用于环保、石油、化工、冶金、食品、环境监测、医药等领域，对国民经济的发展和产品质量的提高发挥着非常重要的作用。为了保证在线分析监测仪器仪表量值的准确可靠［1］，国家出台了一系列国家计量技术规范，对于研究在线分析监测仪器仪表的检校方法有着重要的指导意义。由于在线仪器的监测地点一般是在野外，生产现场及温度、湿度并非恒定的实验室环境，又需要在短时间内实时出具大量检测数据。与实验室环境相比，影响在线数据检测的因素多且变化大，这会导致检测数据波动性大。因此在检校中如果采用GUM法分析数据示值误差的不确定度，不仅工作量大，而且不能马上验算数据的正态性，从而不能验证GUM法是否适用。蒙特卡洛（MCM）法是一种利用对概率分布进行随机抽样而进行分布传播的方法［2-3］，适用于具有任意多个输入量和单一输出量的模型，尤其适用于以下两种情况：

(1)不宜对测量模型进行线性化等类似的场合。

(2)输出量的概率密度函数(PDF)较大程度地偏离正态分布或t分布。

因此在在线仪器校验中，可用蒙特卡洛法评定该仪器示值误差的不确定度，利用GUM法验证蒙特卡洛法是否适用。

笔者以在线pH计的检定为例，利用GUM法验证蒙特卡洛法是否适用于总结在线分析监测仪器仪表示值误差不确定度的分布规律。GUM 法验证结果表明，蒙特卡洛法根据JJF 1547-2015评定在线pH计示值误差不确定度的方法是有效的，适用的。尤其在测量模型非线性以及输出量的概率密度函数（PDF）较大程度地偏离正态分布或t分布等GUM法不适用的场合，蒙特卡洛法是评定在线分析监测仪器仪表示值误差不确定度的必不可少的手段。

1 实验方法

根据JJF 1547-2015 提供的校准方法［4］，选择3种标准溶液（pH 3～10）和标定后的2种标准溶液，测量第3种标准溶液的pH值，重复上述步骤，测量6次，计算平均值pH。

2 蒙特卡洛法的不确定度分析

蒙特卡洛法为不适合使用GUM法评定测量不确定度的场合提出了解决方案，如测量模型非线性、分布明显不对称、输出量的概率密度函数较大程度地偏离高斯分布或t分布等。蒙特卡洛法还能够直观地显示输出量的概率密度曲线。但由于蒙特卡洛法需要对大量的模拟试验数据进行统计分析，手工计算无法完成。按照分布传播的基本原理，笔者开发出一款实用的用蒙特卡洛法评定测量不确定度的应用软件，实现蒙特卡洛法评定测量不确定度的计算。

软件使用VB6编程［5-9］，计算方法采用自适应蒙特卡洛法，保证运算结果收敛性的关键是生成一组（10 000个数据）严格符合规定分布规律的伪随机数，然后用洗牌算法生成后续的伪随机数；提高软件运算效率的关键是测量模型的识别和运算算法；采用低通滤波算法保证概率密度曲线的平滑美观。对于两两相关的输入量，采用的处理方法为首先生成两组相互独立的伪随机数，根据相关系数组合为另两组彼此相关的随机数。利用对概率分布随机抽样进而分布传播的方法，适用于具有任意多个输入量和单一输出量的模型。本软件操作简单，界面友好，可以方便快捷地计算出任意给定测量模型的不确定度。

用蒙特卡洛法［10-13］分析在线pH计的不确定度，影响量与GUM法相同，测量模型：

式中：ΔpH——示值误差；

pHY——被检仪器示值平均值；

pHR——仪器分辨力引起的误差；

pHC——标准溶液的示值；

Ct1——恒温水槽的均匀性引起的修正值；

Ct2——恒温水槽的稳定性引起的修正值；

Ct3——温度探头测温的最大允许误差引起的修正值。

0.01级的在线pH计数学模型以及输入参数的不确定度分析分别见图1和图2，输出的参数包括标准不确定度，扩展不确定度，区间上限、下限等，以及PDF曲线（见图2）。

图1 数学模型及输入参数的不确定度分析（0.01级）

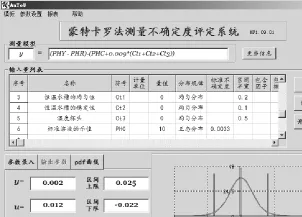
图2 输出参数和PDF曲线（0.01级）

0.1级的在线pH计数学模型以及输入参数的不确定度分析分别见图3和图4，输出的参数包括标准不确定度，扩展不确定度，区间上限、下限等，以及PDF曲线（见图4）。

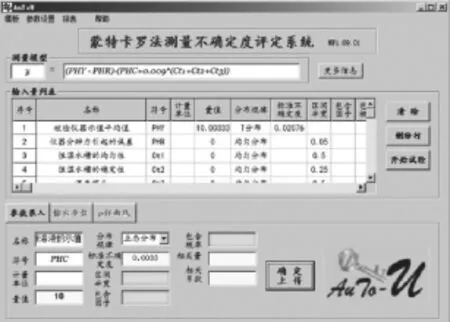
图3 数学模型及输入参数的不确定度分析（0.1级）

图4 输出参数和PDF曲线（0.1级）

3 GUM 法的不确定度分析

根据JJF 1547-2015中附录A，ΔpH不确定度的来源主要有(被检pH计示值的平均值)、 pHs(标准溶液的标准值)，具体分析见JJF 1547-2015附录A。

3.1 标准不确定度和扩展不确定度

由JJF 1547-2015附录A得出被检仪器级别分别为0.01级和0.1级时校准结果的标准不确定度和扩展不确定度，见表1（以校准规范中的A类测量数据为例）。

表1u(ΔpH)的标准不确定度及扩展不确定度

3.2 有效自由度

JJF 1547-2015附录A未计算有效自由度，为了与蒙特卡洛法的不确定度计算结果比较，需要计算，u(pHs)的自由度。

3.2.1u（pH）的自由度

pH 的有效自由度ν（pH）由韦尔奇-萨特思韦特公式计算。当被检仪器为0.01级时，；被检仪器为0.1级时，。

3.2.2u(pHs)的自由度

标准溶液的标准值受以下几个因素影响：标准物质标称值的不确定度、恒温水槽的均匀性、恒温水槽波动性、温度计的示值误差。

(1)标准物质标称值的不确定度u(pHC)的自由度ν(pHC)。估计标准物质标称值不确定度可靠性为90%，则ν(pHC)=50。

(2)温度引起的不确定度u(pHt)的自由度ν(pHt)。其中恒温水槽的均匀性（δ1）、恒温水槽波动性（δ2）、温度计的示值误差（MPE），估计其可靠性为85%，则ν(δ1)，ν(δ2)，ν(MPE)均为22。

ν(pHt)由韦尔奇-萨特思韦特公式计算，当被检仪器为0.01级时，ν(pHt)=29；被检仪器为0.1级时，ν(pHt)=55。

u(pHs)的自由度由韦尔奇-萨特思韦特公式计算，被检仪器为0.01级时，ν(pHs)=77；被检仪器为0.1级时，ν(pHs)=103。

3.2.3 合成标准不确定度的有效自由度

根据韦尔奇-萨特思韦特公式计算，被检仪器为0.01级时，νeff=13；被检仪器为0.1级时，νeff=50。

4 GUM法验证结果

被检校在线pH计的准确度等级分别为0.01级和0.1级时，其采用GUM法和蒙特卡洛法得到的校准结果扩展不确定度见表2。

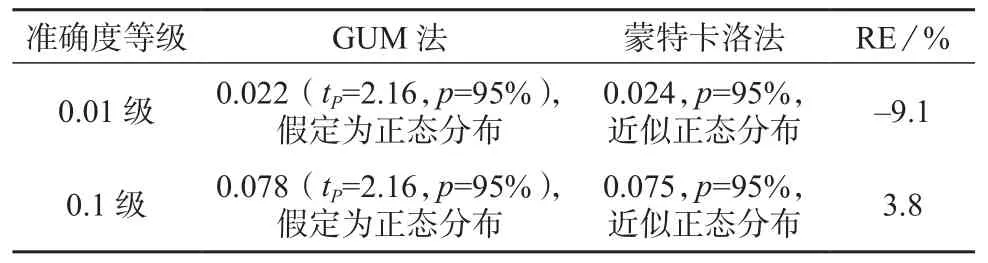
表2 在线pH计校准结果的扩展不确定度

由表2可知，对于0.01级的在线pH计，用GUM法得到的示值误差不确定度比蒙特卡洛法得到的分析结果低9.1%。合成标准不确定度的有效自由度为13，即评估结果的不可靠性为20%。二者差值（9.1%）小于不可靠性（20%），所以GUM法的评估验证结果是可以接受的［14-15］。

对于0.1级的在线pH计，用GUM法得到的示值误差不确定度比蒙特卡洛法得到的分析结果高3.8%。合成标准不确定度的有效自由度为50，即评估结果的不可靠性为10%。二者差值（3.8%）小于不可靠性（10%），所以GUM法的评估验证结果是可以接受的。

5 结语

以在线pH计为例，利用蒙特卡洛法分析在线分析监测仪器仪表示值误差不确定度的分布规律，通过GUM法验证蒙特卡洛法的适用性；利用GUM法验证了蒙特卡洛法根据JJF 1547-2015评定在线pH计示值误差不确定度的方法是有效且适用的。

［1］ 王森.在线分析仪器手册［M］.北京：化学工业出版社，2008.

［2］ JJF 1059.1-2012 测量不确定度评定与表示［S］.

［3］ JJF 1059.2-2012 用蒙特卡洛法评定测量不确定度［S］.

［4］ JJF 1547-2015 在线pH计校准规范［S］.

［5］ 周宁宁.基于MCM的不确定度评定软件开发［J］.中国测试，2015，41(z1)： 45-48.

［6］ 杨建.蒙特卡罗法评定测量不确定度中相关随机变量的MATLAB实现［J］.计测技术，2012，32(4)： 51-54.

［7］ 崔伟群.基于蒙特卡罗方法评定不确定度中相关随机变量模拟［J］.现代测量与实验室管理，2010，18(4)： 24-27.

［8］ 刘继义.正态分布的近似算法在不确定度分析中的应用［J］.中国计量，2008(9)： 88-89.

［9］ 杨图强.基于MATLAB的MCM对GUM不确定度框架验证［J］.质量技术监督研究，2014(6)： 32-36.

［10］ 高惠旋.统计计算［M］.北京：北京大学出版社，1995.

［11］ 米小琴.统计计算与分析［M］.北京：清华大学出版社，2004.

［12］ 刘智敏.统计t分布的新计算与应用［J］.中国计量学院学报，2004，15(1)： 1-12.

［13］ 周桃庚.用蒙特卡洛法评定测量不确定度［M］.北京：中国质检出版社，2013.

［14］ 冯亚南.对GUM法量块测量不确定度评定的验证［J］.计测技术，2013，33(s2)： 62-64.

［15］ 曹芸.采用MCM对GUM法测量不确定度评定的验证方法研究［J］.宇航计测技术，2012，32(2)： 75-78.

炉渣中钙含量的测定方法

申请公布号：CN106404776A申请公布日：2017.02.15

申请人：攀钢集团江油长城特殊钢有限公司

摘要本发明涉及化学分析技术领域，公开了一种炉渣中钙含量的测定方法，该方法包括：(1)将炉渣制成溶液，并向该溶液中依次加入EDTA溶液、氨水、草酸溶液和乙酸混合反应，得到沉淀物；(2)将步骤(1)获得的沉淀物用pH值为4～5的含有EDTA和草酸的乙酸-乙酸铵缓冲液洗涤；(3)将经步骤(2)洗涤后的沉淀物用硝酸和高氯酸分解；(4)使用EDTA标准溶液滴定经步骤(3)分解处理后的混合物中的钙含量。本发明提供的炉渣中钙含量的测定方法步骤简单，精确度高，重复性好，选择性高。

一种进样器和自动进样方法

申请公布号：CN106443033A申请公布日：2017.02.22

申请人：济南海能仪器股份有限公司

摘要本发明公开了一种进样器和自动进样方法，属于分析仪器技术领域。其中进样器包括：至少一个升降机构，用于带动装载于其上的支架做升降运动；至少一个支架，每个支架对应装载于一个升降机构上，支架上具有安装孔，用于装载包括测量电极、搅拌棒和滴定管的部件；载杯盘，载杯盘与每个支架之间能够相对旋转；至少一个样品杯，样品杯装载于载杯盘上，样品杯的杯口与支架上装载的测量电极、搅拌棒和滴定管都对准。本发明具有实验速度快的优点，能够实现复数自动上样，且样本位和清洗位的位置和数量可设定。

一种光谱分析仪分时共享测试系统

申请公布号：CN106385401A申请公布日：2017.02.08

申请人：何桂崧

摘要本发明提出了一种光学频谱分析仪分时共享测试系统，由服务器电脑(安装Server软件)、光谱扫描分析仪、光开关盒、测试器件组、客户端电脑组(安装Client软件)组成；利用软件和网络等技术实现多个测试工位分时共享一套光谱分析仪器，提高光谱分析仪器的使用效率，同时提高了产能。

适用于自动化免疫分析仪器的板间移液装置

申请公布号：CN106443040A申请公布日：2017.02.22

申请人：盐城拜明生物技术有限公司

摘要本发明提供了适用于自动化免疫分析仪器的板间移液装置，能解决现有技术中因待检测的96孔微孔板摆放偏差导致的仪器检测误差大的技术问题。包括移液器、X轴移动装置、Y轴移动装置和Z轴移动装置，其特征在于：还包括夹爪以及与夹爪对应的定位片，夹爪包括一对夹板以及驱动该对夹板相向移动或相反移动的驱动装置；X轴移动装置的滑座上支撑有Y轴移动装置，Y轴移动装置的滑座上设有一连接架，连接架两侧各设有一Z轴移动装置，其中一个Z轴移动装置的滑座上固定有移液器，另一个Z轴移动装置的滑座上固定有夹爪。

样本分析仪

申请公布号：CN106383242A申请公布日：2017.02.08

申请人：杭州昕龙医疗科技有限公司

摘要本发明公开了一种样本分析仪，包括底板、固定于底板的工作台、试管架运转机、预处理装置、滴液结构、化学分析装置及镜检分析装置。试管架运转机及预处理装置固定安装于底板，滴液结构滑动安装于工作台，化学分析装置及镜检分析装置固定于工作台。试管架运转机带动试管在底板移动，预处理装置将拭子上的样本溶解至试管的溶液中，滴液结构将溶液分别滴至计数池及试纸上，化学分析装置对试纸上的溶液进行化学分析，镜检分析装置对计数池上的溶液进行分析。本发明样本分析仪的试管架运转机使试管自动移动，预处理装置将拭子上的样本溶解至试剂中，滴液结构、化学分析装置及镜检分析装置自动分析样本，使样本的分析工作自动完成。

Uncertainty Evaluation of Indication of On-line pH Meters by MCM

Zhou Ningning, Sun Qianyun, Liu Jiyi, Gao Jie, Li Fen, Zhao Daolin
(Shandong Institute of Metrology, Jinan 250014, China)

Taking the on-line pH meter as an example, the distribution of uncertainty of indication error of the on-line pH meter was investigated, MCM method was used for the uncertainty analysis of the indication error. For 0.01 level online pH meter, the difference between two methods of MCM and GUM was 9.1%, which was less than the unreliability (20%); for 0.1 level on-line pH meter, the difference between the two methods was 3.8%, which was less than the unreliability (10%). A conclusion was gained that GUM method was suitable to verify the validity of MCM for evaluating the uncertainty of the indication error of on-line pH meter according to JJF 1547-2015. Especially in the situations which were not suitable for GUM method (the measurement model was nonlinear and the output PDF deviates from the normal distribution ortdistribution), MCM was an important method to evaluate the uncertainty of indication error of on-line analytical and monitoring instruments.

on-line analysis and monitoring; on-line pH meter; GUM method; MCM method; verification

O651

:A

:1008-6145(2017)02-0102-04

10.3969／j.issn.1008-6145.2017.02.028

联系人：周宁宁；E-mail： 1215596795@qq.com

2016-12-22