高二上学期期末全国名校综合测试卷

■河南师范大学附属中学 孟召臣

高二上学期期末全国名校综合测试卷

■河南师范大学附属中学 孟召臣

一、选择题(本大题共12小题,每小题5分,共60分。每小题只有一个选项符合题意)

1.已知p:α为第二象限角,q:sinα＞cosα,则p是q成立的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

2.在△ABC中,已知a=x,b=2,B= 45°,如果利用正弦定理解三角形有两解,则x的取值范围是( )。

A.x＞2 B.x＜2

3.若四个正数a、b、c、d成等差数列,x是a和d的等差中项,y是b和c的等比中项,则x、y的大小关系为( )。

A.x＜y B.x＞y C.x=y D.x≥y

4.不等式x(2-x)＜x(1+x)的解集是( )。

A.(-∞,-1)∪(2,+∞)

B.(-∞,0)∪(1,+∞) 2

C.(-1,2)

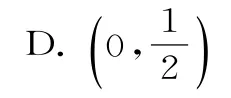
5.等差数列{an}中,若a4+a6+a8+a10+ a12=120,则的值是( )。

A.14 B.15 C.16 D.17

6.已知命题“∀a、b∈R,如果ab＞0,则a＞0”,则它的否命题是( )。

A.∀a、b∈R,如果ab＜0,则a＜0

B.∀a、b∈R,如果ab≤0,则a≤0

C.∃a、b∈R,如果ab＜0,则a＜0

D.∃a、b∈R,如果ab≤0,则a≤0

7.在锐角△ABC中,若tanA=t+1, tanB=t-1,则t的取值范围为( )。

D.(-1,1)

8.已知函数解析式为f(x)=把函数()() ,gx=fx -x+1的零点按从小到大的顺序排列成一个数列,并且该数列的前n项和为Sn,那么S10=( )。

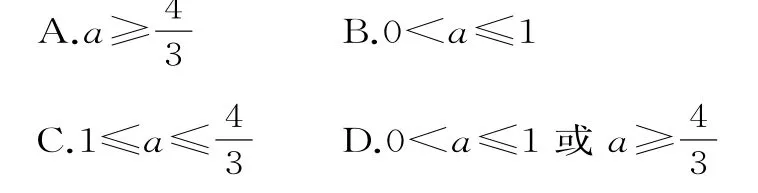
A.29-1 B.210-1 C.55 D.459.若不等式组表示的平面区域是一个三角形,则实数a的取值范围为( )。10.设P为双曲线上的一点, F1、F2是该双曲线的两个焦点,若|PF1|∶|PF2|=3∶2,则△PF1F2的面积为( )。

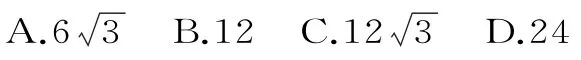
11.已知各项均为正数的等比数列{an}满足a7=a6+2a5,若存在两项am,an使得,则的最小值为( )。

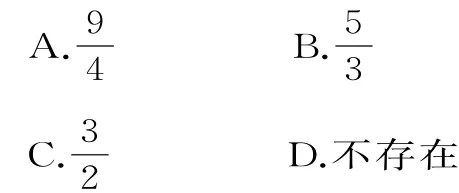
12.已知A(3,0),O是坐标原点,点P(x,y)的坐标满足则的取值范围为( )。

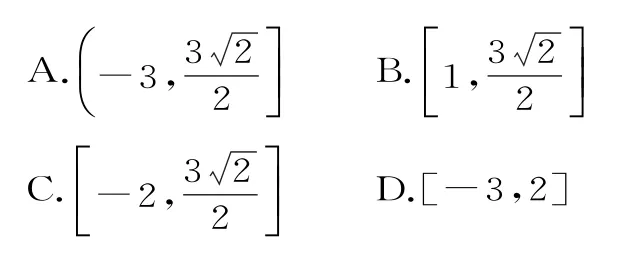
二、填空题(本大题共4小题,每小题5分,共20分)

13.已知Sn,Tn分别是等差数列{an}, {bn}的前n项和,且,则=____。

14.已知a、b、c分别为△ABC中角A、B、C的对边,且满足a+c=2b,C=2A,则sinA=____。

15.已知a、b＞0,a+b=4,则+的最大值为____。

16.已知F1、F2为椭圆(a＞b＞0)的左、右焦点,点P为椭圆C上任一点,△F1PF2的内心为I。若存在实数λ满足:(1+λ)则椭圆C的离心率为____。

三、解答题(本大题共6小题,共70分。请写出必要的解题步骤)

17.(本小题满分10分)设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+的值域,集合C为关于x的不等式(x+4)≤0,a∈R的解集。

(1)求A∩B。

(2)若C⊆∁RA,求实数a的取值范围。

18.(本小题满分12分)在斜三角形ABC中,角A、B、C的对边分别为a、b、c。

19.(本小题满分12分)已知数列{an}满足a1=1,且8an+1an-16an+1+2an+5=0 (n≥1)。记bn=(n≥1)。

(1)求b1,b2,b3,b4的值。

(2)求数列{bn}的通项公式及数列{anbn}的前n项和Sn。

20.(本小题满分12分)在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2py(p＞0)相交于A、B两点。

(1)若点N是点C关于坐标原点O的对称点,求△ANB面积的最小值。

(2)是否存在垂直于y轴的直线l,使得l被以AC为直径的圆截得的弦长恒为定值?若存在,求直线l的方程;若不存在,说明理由。

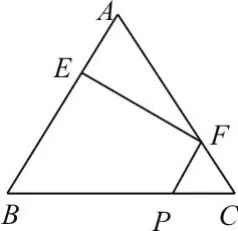
图1

21.(本小题满分12分)如图1,在边长为3的正三角形ABC中,E、F、P分别为AB、AC、BC上的点,且满足AE= FC=CP=1。将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B为直二面角,连接A1B, A1P,如图2所示。

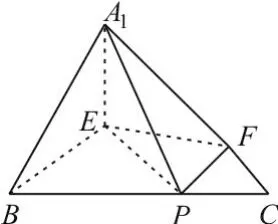
图2

(1)求证:A1E⊥平面BEP。

(2)求直线A1E与平面A1BP所成角的大小。

22.(本小题满分12分)如图3,梯形ABCD的底边AB在y轴上,原点O为AB的中点,,AC⊥BD,M为CD的中点。

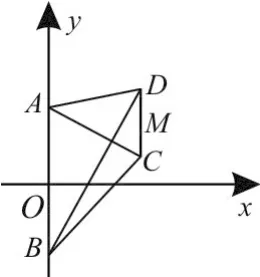
图3

(1)求点M的轨迹方程;

(2)过M作AB的垂线,垂足为N,若存在正常数λ0,使,且P点到A、B的距离和为定值,求点P的轨迹E的方程。

1.A2.C3.D4.B5.C6.B 提示:命题“若p,则q”的否命题为“若非p,则非q”。故选B。

7.A 提示:tanA＞0,tanB＞0⇒t＞1。再由tanC=-tan(A+B)=可得t＞。

8.D 提示:作出f(x)和y=x-1的图像,可知g(x)=f(x)-x+1的零点为自然数列,即an=n-1,故S10=45。

9.D 提示:由所构成的平面区域为图4中△OAG及其内部,其中,A(1,0)斜率为-1的直线与x轴交点在线段OA上(不含O点)或在点B的右侧时构成的平面区域为三角形区域,故0＜a≤ 1或

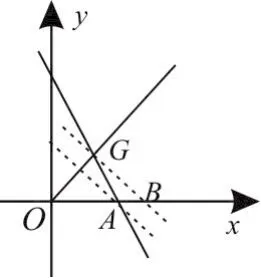
图4

10.B 提示:因为|PF1|∶|PF2|=3∶2,可设|PF1|=3x,|PF2|=2x,根据双曲线定义得|PF1|-|PF2|=x=2a=2,所以|PF1|=6,|PF2|=4,|F1F2|=2。

11.C 提示:因为a7=a6+2a5,所以q2-q-2=0,q=2或q=-1(舍去)。故m+n=6。

12.A 提示:作出可行域如图5(其中不包括线段OC)。

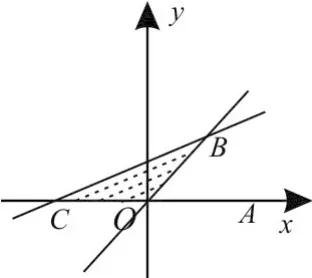
图5

13.

14

15.提示:令ab+1=t,由 4=a+b≥2得0＜ab≤4,1＜t≤5。原式

16提示:设△F1PF2的重心为G,则满足:

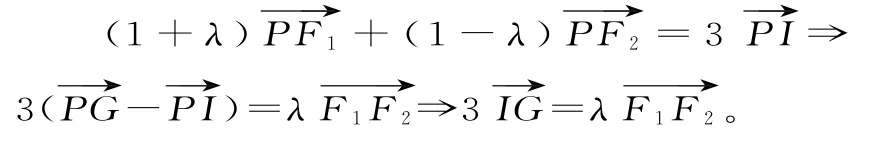
故设P(x,y),则△F1PF2的内切圆半径

17.(1)由于-x2-2x+8＞0,解得A= {x|-4＜x＜2}。

B={x|x≤-3或x≥1}。

A∩B={x|-4＜x≤-3或1≤x＜2}。

(2)∁RA={x|x＜-4或x≥2}。

18.(1)由正弦定理得

2sinAcosC=sinB可化为2acosC=b。

(2)在斜三角形ABC中满足A+B+ C=π。

sin(2A+B)=3sinB可化为: sin[π+(A-C)]=3sin[π-(A+C)]。

故-sin(A-C)=3sin(A+C)。

故-sinAcosC+cosAsinC= 3(sinAcosC+cosAsinC)。

整理得4sinAcosC=-2cosAsinC。

19.(1)由得代入递推关系式8an+1an-16an+1+2an+5= 0,整理得

由a1=1,得b1=2。

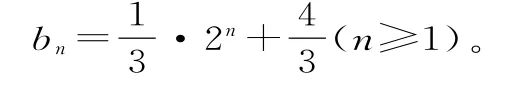
故Sn=a1b1+a2b2+…+anbn=

20.(1)依题意知,点N的坐标为N(0, -p),可设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+p。与x2=2py联立得消去y得:

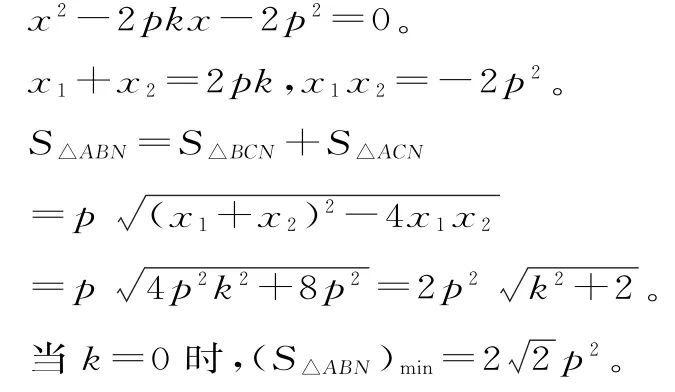
(2)假设满足条件的直线l存在,其方程为y=a,AC的中点为O',l与AC为直径的圆相交于点P、Q,PQ的中点为H,则O'H⊥ PQ,Q'点的坐标为

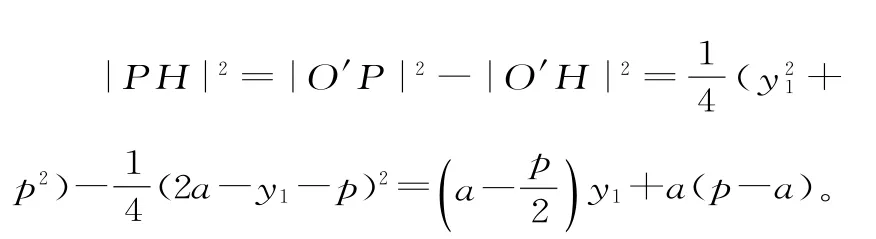
因此,|PQ|2=(2|PH|)2=

21.(1)取BE中点D,连接DF。因为AE=CF=1,DE=1,所以AF=AD=2。而∠A=60°,即△ADF是正三角形。

又因为AE=ED=1,所以EF⊥AD。

所以图2中,有A1E⊥EF,BE⊥EF。

∠A1EB为二面角A1-EF-B的平面角。

又二面角A1-EF-B为直二面角,所以A1E⊥BE。

又因为BE∩EF=E,所以A1E⊥平面BEP。

(2)由(1)可知A1E⊥平面BEP,BE⊥EF。如图6,以E为原点,建立空间直角坐标系E-xyz,则E(0,0,0),A1(0,0,1), B(2,0,0),F(0,0)。连接DP。

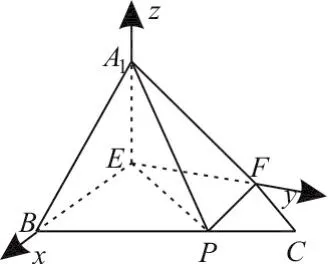
图6

不妨设平面A1BP的法向量n=(x,y, z),则即

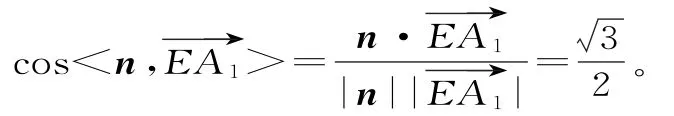
故直线A1E与平面A1BP所成角的大小为

22.(1)设点M的坐标为M(x,y)(x≠0),则

(2)设P(x,y),则M((1+λ0)x,y),代入M的轨迹方程有(1+λ0)2x2+y2=1(x≠ 0),即

点P的轨迹为椭圆(除去长轴的两个端点)。

解得λ0=2,从而所求点P的轨迹方程为9x2+y2=1(x≠0)。

设P(x1,y1),Q(x2,y2),则x1+x2=

(责任编辑 徐利杰)