弃繁就简，直达成功——谈谈抛物线问题的优化策略

■江苏省太仓市明德高级中学 王佩其

弃繁就简，直达成功
——谈谈抛物线问题的优化策略

■江苏省太仓市明德高级中学 王佩其

所谓解析几何,就是用代数的方法解决几何问题。而代数讲究的是运算,倘若解题方法不当,往往无法“将计算进行到底”,因此,同学们在平时解题时要探求优化运算的方法和技巧,降低运算量。那么在抛物线问题中,哪些策略能让我们弃繁就简,直达成功呢?

策略一:巧用定义,把握动点、焦点、准线三者互化

如图1,已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是____。

图1

分析:注意到l2:x=-1是抛物线y2=4x的准线,故可将抛物线上点P到直线l2:x=-1的距离转为它到焦点的距离,再依据几何图形,可轻而易举求出距离之和的最小值。

解:因为抛物线的方程为y2=4x,所以焦点坐标为F(1,0),准线方程为x=-1。设P到准线的距离为|PB|,则|PB|= |PF|。P到直线l1:4x-3y+6=0的距离为|PA|,所以|PA|+|PB|=|PA|+|PF|≥|FD|,其中|FD|为焦点到直线4x-3y+ 6=0的距离。又,故距离之和最小值是2。

点评:在抛物线的问题中,通过焦点弦或焦半径,与相关点到准线的距离之间可相互转化,避免了解方程组的烦琐,减少运算量。

策略二:巧用“点差”,速解弦所在直线的斜率

在抛物线问题中,直线与抛物线的相交弦问题是高考热点,其解法多种多样,“点差法”是其中一个巧妙的解题方法。“点差法”将弦所在的直线斜率、弦上的点坐标联系起来,相互转化,能起到事半功倍的效果。

过抛物线y2=x上的点A(4,2)作倾角互补的两条直线AB、AC,交抛物线于B、C,则直线BC的斜率为____。

分析:本题虽未涉及弦的中点,但A、B、C三点都在抛物线上,并探究的是三条弦的斜率关系,故可采用点差法。

解:设B(x1,y1),C(x2,y2),代入抛物线方程得:

①②两式作差整理得:

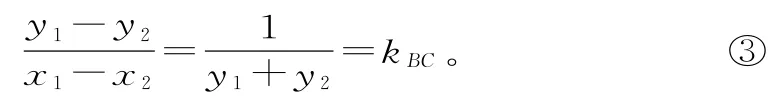
又因kAC=-kAB,整理得y1+y2=-4。代入③即得到直线BC的斜率为

点评:点差法在解析几何问题中经常用到,同学们一定要熟练应用。

策略三:数形结合,把握几何图形的特征

解析几何既有代数特性,又有几何特征,倘若我们在研究抛物线问题时,既能抓住抛物线的“个性”,又能把握住平面几何的特性,那么常常可以找到通向成功的“捷径”。

过抛物线x2=2py(p＞0)的焦点F作倾斜角为30°的直线,与抛物线分别交于A、B两点(点A在y轴左侧),则=____。

分析:依据图形特征,可将|AF|与|FB|之比转化为点A与点C两点的横坐标的绝对值之比。

图2

解法一:如图2,作AA'⊥x轴,BB'⊥x轴,则AA'∥FO∥ BB'。所以已知xA＜0,xB＞0,则因为直线AB方程为所以与x2=2py联立得

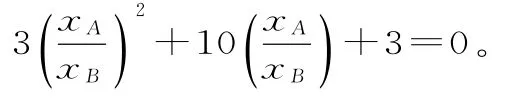
解法二:设AF=m,BF=n。如图2,过A作AC⊥BB'于C,则由抛物线的焦半径公式可得

所以|BC|=|BB'|-|AA'|=n-m。

在Rt△ABC中,由于∠BAC=30°,故|AB|=2|BC|。

m+n=2(n-m)。

点评:解法一注重代数运算,解题过程比较烦琐,而解法二注重抛物线的定义和图形的几何性质的应用,解题过程简洁明了。从本例可以看出,注重图形的几何特征,有时能简化解题过程。

策略四:设而不求,整体代换

在抛物线问题中,对相关点的坐标设而不求,进而建立方程(组),并运用韦达定理整体代换,可避免求交点,简化解题过程。

已知抛物线y2=4x,过点(0,-2)的直线交抛物线于A、B两点,O为坐标原点。若,求直线AB的方程。

分析:设直线AB的方程为y=kx-2 (k≠0),A(x1,y1),B(x2,y2),由得x1x2+y1y2=4。将直线方程与抛物线方程联立,运用韦达定理,整体代换可求出k。

解:(1)设直线AB的方程为y=kx-2 (k≠0),代入y2=4x得:

设A(x1,y1),B(x2,y2),则x1+x2=

又由方程①的判别式Δ=(4k+4)2-16k2＞0得故k=-1+。

点评:“设而不求,整体代换”,不仅可以用来求曲线的方程,而且可以解决抛物线中涉及弦长、弦中点、曲线与直线交点以及原点为垂足的垂直问题和定值定点问题。但必须注意对有关一元二次方程的根的存在性用判别式Δ加以检验。

(责任编辑 徐利杰)