基于有限元方法的混凝土泵车结构疲劳寿命预测
2017-03-23田相玉黄大为周志红
田相玉,黄大为,周志红
(国家混凝土机械工程技术研究中心,长沙 410013)
布料杆是混凝土泵车实施作业时的主要承载机构,其可靠性直接影响到泵车的工作性能和安全性.泵车作业时工况多种多样,油缸的伸展变幅和混凝土的冲击载荷等造成布料杆在垂直平面内振动,布料杆作为典型的薄壁箱型焊接梁结构,上下盖板处将承受交变载荷作用.布料杆振动一方面会影响布料精度和操作安全性,另一方面会增大危险截面处的动应力幅值和频次,加速疲劳损伤累计而降低疲劳寿命.
根据工程机械行业统计数据,由疲劳断裂引起的结构破坏占泵车失效故障的90%左右.国内外许多学者对布料杆的疲劳寿命进行了研究,但集中在基于理论力学模型和疲劳损伤累计等的解析法[1-3],研究对象大多为几何外形简单的截面或构件.本文提出的基于有限元仿真的布料杆疲劳寿命预测的方法,能对结构复杂的截面或构件进行疲劳寿命分析,并在疲劳试验台上进行试验验证,对提高布料杆的可靠性设计提出了一种新的解决思路.
1 疲劳强度计算
结构的疲劳强度取决于结构的工作级别(应力谱和应力循环次数)、构件连接类别、结构件材料种类、结构件的最大应力和应力循环特性等.
1.1 分析流程
本文在校核布料杆静强度的基础上,结合疲劳许用应力理论计算模型,提出了一种简便时效的有限元疲劳强度校核方法,如图1所示.

图1 疲劳强度校核基本流程Fig.1 The basic process of checking fatigue strength
首先,根据设计输入条件,建立布料杆的三维模型,并进行机构运动仿真分析,求出各构件的时间历程载荷谱.然后,将三维实体模型导入Hyper Mesh中,抽取中面、网格划分、材料和单元属性定义、局部坐标系建立、边界条件施加等.再将计算模型导入有限元分析软件ANSYS中求解,并提取关键部位(或高应力区)的结果.最后,按照疲劳许用应力理论计算模型进行校核.
1.2 应力集中系数确定[4]
按应力集中情况,将非焊接件构件连接分为W0一个应力集中情况等级,将焊接件构件连接分为K0,K1,K2,K3和K4等5个应力集中情况等级.在每个应力集中情况等级中,又有1种或多种不同的构件接头型式,见GB/T 3811—2008附录O.
随着连接应力集中等级的递增,结构疲劳强度递减.在疲劳强度校核时,应综合考虑现有的生产组织和质量控制水平,尽量采用较为合理的应力集中情况等级Ki值.本文推荐采用K2,尽量避免采用K4.
1.3 许用应力确定
通常结构的应力循环特性r越小,则疲劳强度越低,对称循环(r=-1)的疲劳强度最低,最易破坏.因此,金属结构常以应力对称循环的疲劳强度极限σ-1为基准,其他应力循环特性的疲劳强度则依此进行换算.
对称循环的疲劳强度极限σ-1由材料的疲劳试验得到,考虑安全系数(取1.34)后即可得到疲劳许用应力基本值[σ-1].非对称循环的疲劳许用应力[σr]以[σ-1]为基准和计算部位的应力比r,由表1所列公式求得对应应力比的疲劳许用应力[σr]和[τr].

表1 疲劳许用应力计算公式Tab.1 The calculation formula of fatigue allowable stress
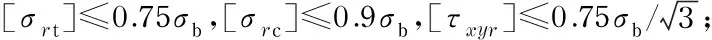
由材料的疲劳试验可知,相同的材料,当应力循环特性r不同时,疲劳曲线不同,但循环基数大致相同,为2×106.基本疲劳许用应力[σ-1]的所有数值是以工作级别E8(n/2×10-6,Ksp=1)为基础,推算出其他所有级别E1~ E7时的[σ-1]所有值.
按照表1的所列的许用应力计算公式,结合前期对高强钢的基础疲劳试验研究成果,本文给出了高强钢在不同工作级别、不同连接类型下的疲劳许用应力基本值,如表2所示.
1.4 名义应力确定
名义应力是不考虑接头本身引起的应力集中,而在相关截面上计算出的弹性应力,应考虑接头附近构件的宏观几何形状不连续导致的应力集中,如开孔、截面变化等.对于简单结构,可用材料力学的理论计算公式即可确定出名义应力;对于复杂结构形式的名义应力,不可能使用解析方法求解,可采用有限元计算方法,但要注意有限元模型中须排除任何引起应力增加的焊接接头结构细节.
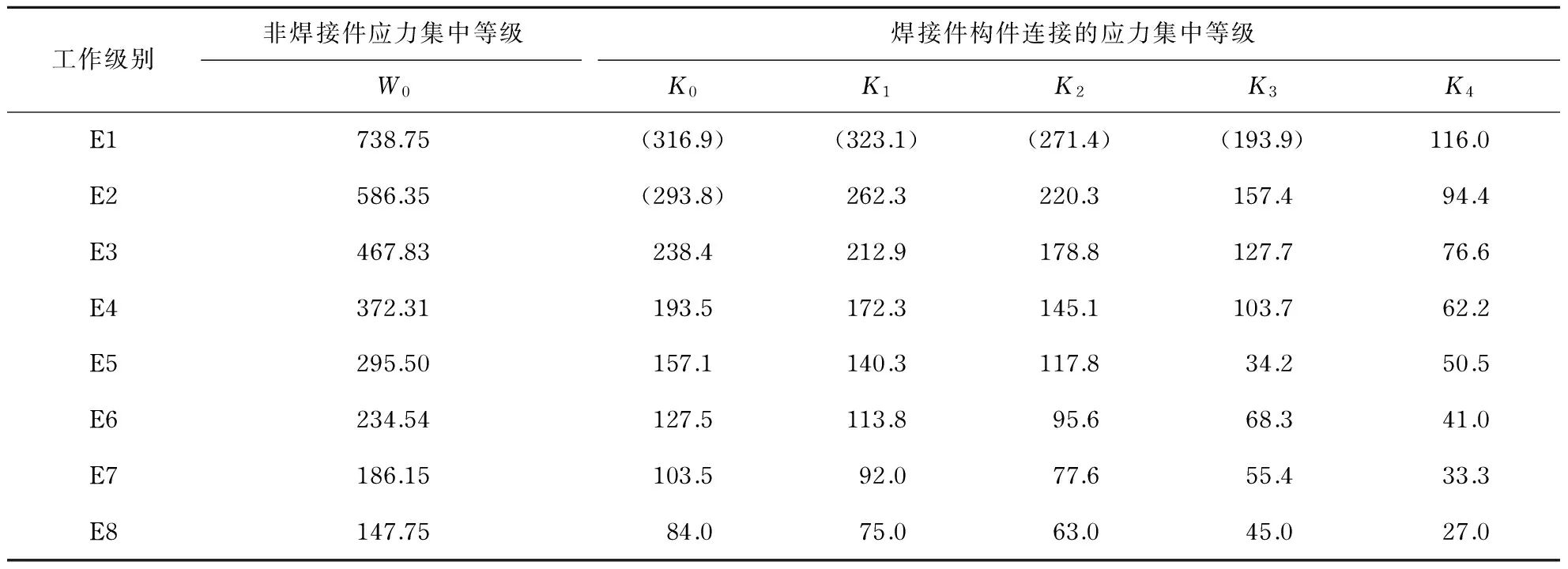
表2 疲劳许用应力的基本值Tab.2 The basic value of fatigue allowable stress MPa
注:括号内数值为大于σb的理论计算值.
布料杆结构相对复杂,评估其疲劳寿命应使用名义应力,且选择合适的名义应力参考点.对于非焊缝区域,选择应力最大的点作为名义应力参考点.对于焊缝区域,选择距焊缝一定距离(通常取距焊趾2倍板厚),且应力绝对值最大的点作为参考点,如图2所示.
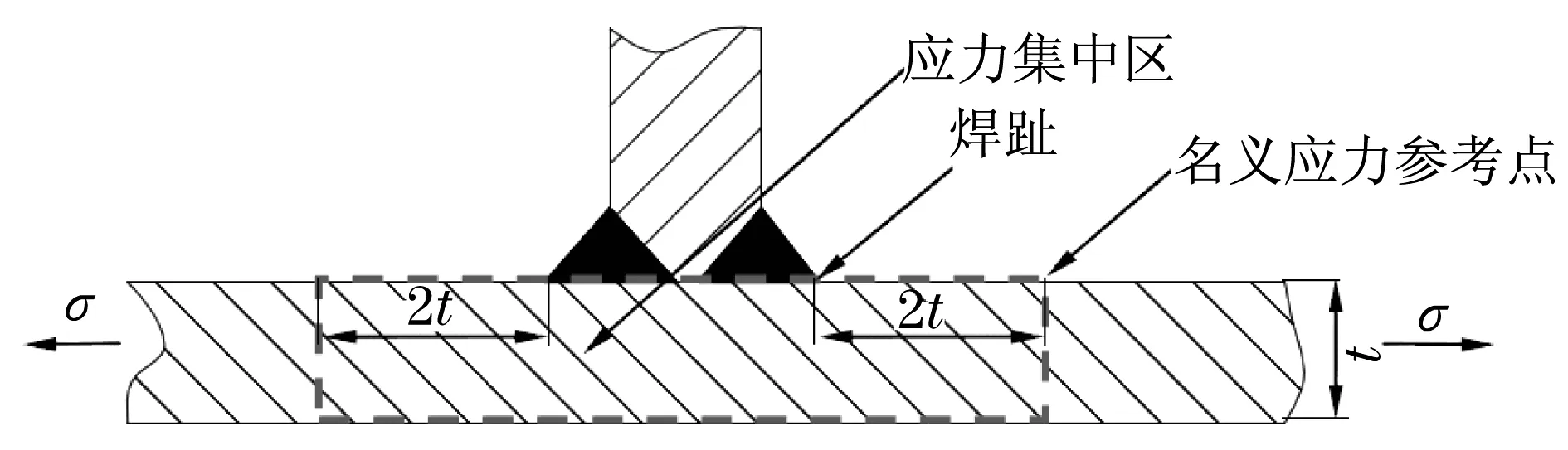
图2 应力集中几何示意图Fig.2 The geometry diagram of stress concentration
当名义应力与焊缝成一定角度θ时,应将全局坐标系下参考点的应力状态转换成局部焊缝坐标系下的相应状态,如图3所示.在模型中建立局部焊缝坐标系,x轴应与焊缝保持垂直,y轴应与焊缝保持平行;将结果映射到局部坐标系,即可求得应力分量[σ⊥],[τ⊥∥],见式(1)和式(2).

图3 斜对接焊缝名义应力坐标变换图Fig.3 The coordinate transformation diagram of diagonal butt weld nominal stress
(1)
(2)
1.5 疲劳强度校核
计算疲劳强度时,所选截面应是应力循环中产生最大正应力、剪应力,或两者都比较大的位置.疲劳计算时的最大应力不是采用等效载荷计算的,而是按照作用在构件上的基本载荷(自重载荷、工作载荷和惯性载荷等)计算的,将影响结构疲劳强度的其他因素都放入疲劳许用应力中去考虑.
1.5.1非焊接区域
对非焊接头区域(或母材)按第4强度理论进行校核:
(3)
式中:σ1,σ2,σ3为参考点的第1,2和3向主应力;[σr]为参考点的疲劳许用应力.当r=0时,单向主应力中绝对值最大的主应力的正负决定了受拉还是受压状态.
有限元分析完毕后处理时,提取参考点的综合应力(Von-Mises)与[σr]作比较分析,即可校核对应位置区域的疲劳强度.
1.5.2焊接接头区域
对焊接区域进行如下疲劳强度校核:
σmax≤[σr]
(4)
τmax≤[τr]
(5)
(6)
式中:σmax,τmax为最大正应力和最大剪应力;σxmax,σymax,τxymax为x,y向最大正应力,xoy平面最大剪应力;[σr],[σrx],[σry],[τrxy],[τr]为疲劳许用正应力和剪应力.
当按式(4)~(6)校核参考点处的疲劳强度时,应在局部焊缝坐标系下,比较参考点处的主应力、剪切应力(Sx,Sy及Sxy)和对应方向应力下的许用疲劳强度即可,最后按照式(6)核算焊缝的疲劳安全比.
2 实例分析
本文以某型号泵车的3节臂在水平工况下的可靠性设计为例,阐述布料杆的疲劳寿命预测过程.首先,根据该布料杆的RZ型折叠结构形式,初步拟定每节臂的应力循环特性r,如图4所示,其中3节臂的应力比r=0.

图4 布料杆整体应力循环特性Fig.4 The overall stress cycle characteristics of the placing boom
布料杆有限元分析模型采用板-梁组合单元,本体采用SHELL 63单元,砼管支撑和销轴采用beam 188单元,输送管采用pipe 18单元,连杆和油缸采用link 8单元.针对关注的焊缝区域,网格需细化,由于本文中分析对象为斜对接,建立了焊缝局部坐标系,如图5所示.

图5 疲劳分析有限元模型Fig.5 The finite element model of fatigue analysis
非焊接区域(或母材)的校核按照第4强度理论,提取3节臂水平工况下应力较大区域的Von-Mises应力,如图6所示.根部下盖板区域在水平工况下的第3主应力约为-450 MPa,且三向主应力中绝对值最大者,则重点关注区域处受力状态为单向压缩,而单向压缩许用应力为700 MPa,满足设计要求.

图6 非焊接区域疲劳强度校核Fig.6 The fatigue strength check of non-welded area
对于焊接接头,按照校核流程,首先确定关注焊缝的应力集中系数Ki,本文选取的分析对象为上盖板焊件上的t12对t8对接焊缝接头,设计时采用1∶5的斜坡平缓过渡,下料时机加斜坡段和V形坡口,焊接时采用引弧板、双面焊,并进行射线探伤,故定义其应力集中系数为K2.然后,选取距焊缝2倍距离处的节点集为分析对象,取主应力绝对值最大的作为名义参考点,分别校核主应力、剪切力和安全比,如图7所示.若参考点与单元节点不重合时,应采用ANSYS路径映射技术,选距该应力参考点相邻的节点进行线性插值,且所选择的插值点应位于非应力集中区内,并与参考点呈线性关系.

图7 对接焊缝疲劳强度校核Fig.7 The fatigue strength check of butt weld
通过有限元仿真分析,设计者可以清晰地了解布料杆的应力分布和疲劳强度相对薄弱的部位.结合疲劳许用应力理论计算模型,可对布料杆的疲劳寿命进行预测.
3 台架疲劳试验[5]
考虑混凝土泵车在实际工作中工况组合的多样性和随机性等特点,本文以被考核构件受力最大(或最恶劣工况)为原则设计了8种典型的试验工况,考虑构件间的相互作用和疲劳损伤累计等,每一工况中被考核构件的载荷循环次数按一定规律呈线性分布,如图8所示.
为使构件的台架疲劳强度试验接近于设备实际使用时的载荷分布,试验前需采集类似型号产品在各种典型工况下的时间载荷历程数据集,统计分析后结合本产品的载荷数据,拟合出研究对象的载荷谱.表3为理论研究对象的目标试验载荷.
另外,为提高台架试验结果的精确性以及与数值分析的匹配性等,亦可将试验载荷谱作为边界条件,对所设计的结构进行疲劳强度分析,估算出其疲劳使用寿命T1,待台架试验完毕统计分析出构件的试验寿命T2,比较分析两者的异同.
综合理论计算和疲劳试验的结果,研究对象的台架疲劳寿命与有限元仿真的疲劳寿命趋势一致,较为吻合,且布料杆疲劳开裂的部位主要集中于应力集中区,如对接焊缝、漏水孔等其他受载情况恶劣的部位,如图9所示.

图8 疲劳试验结构件工况分配Fig.8 The condition distribution of fatigue test structure
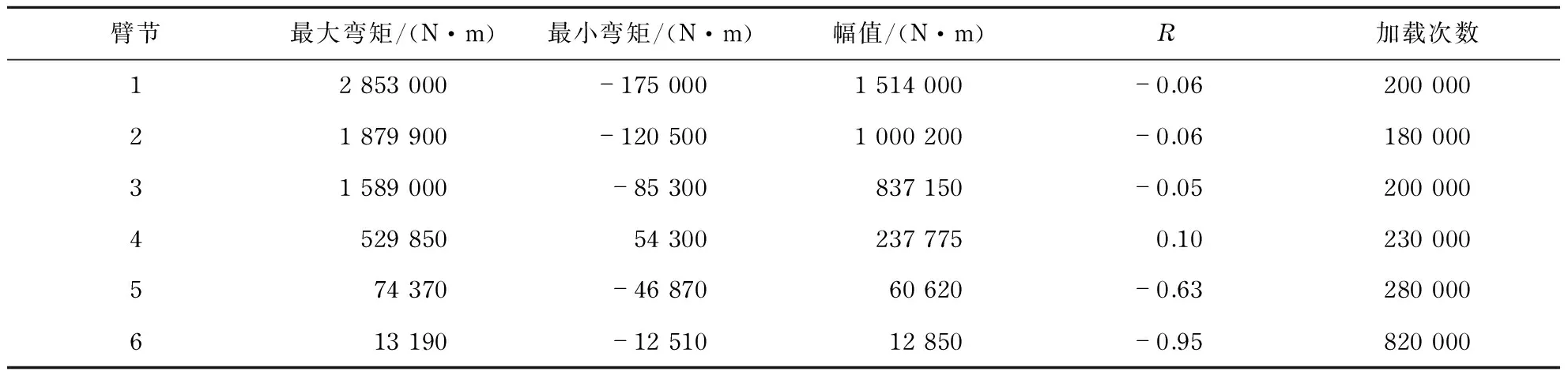
表3 臂架疲劳试验目标载荷Tab.3 The target load of placing boom fatigue test

图9 疲劳试验结果Fig.9 The results of fatigue test
4 结论
(1) 结合分析实例,阐述了基于有限元方法的预测疲劳寿命的基本步骤,简便时效.
(2) 有限元仿真分析的结果和疲劳试验的结果较为吻合,表明计算方法的正确性.
(3) 在设计承受交变载荷的焊接结构时,应以焊接接头的疲劳强度作为整体结构的疲劳强度.采取有效的工艺措施,严格控制焊接质量,减少或防止焊接缺陷的产生,保证焊接结构的制造质量满足设计要求.
(4) 设计者应增加对焊接结构抗疲劳强度的了解,合理设计截面和布置焊缝,选择最优的结构形式或接头形式,使所设计的焊接结构更合理,具有更高的疲劳强度.
[1] 范小宁,徐格宁,杨瑞刚.基于损伤-断裂力学理论的起重机疲劳寿命估算方法[J].中国安全科学学报,2011,21(9):58-63.
FAN X N,XU G N,YANG R G.Fatigue life prediction of crane based on damage-fracture mechanics[J].China Safety Science Journal,2011,21(9):58-63.
[2] 殷玉枫,曾光,徐格宁,等.起重机箱型梁疲劳裂纹与寿命预估[J].中国工程机械学报,2010,8(3):274-278.
YIN Y F,ZENG G,XU G N,et al.Fatigue cracks and life estimation for crane box girders[J].Chinese Journal of Construction Machinery,2010,8(3):274-278.
[3] 刘克格,阎楚良,张书明.模糊数学在疲劳寿命估算中的应用[J].航空学报,2006,27(2):227-231.
LIU K G,YAN C L,ZHANG S M.Fatigue life estimation for using fuzzy mathematics[J].Acta Aeronauticaet Astronautica Sinica,2006,27(2):227-231.
[4] 彼德森.应力集中系数[M].北京:国防工业出版社,1988.
PETERSON R E.Stress concentration factor[M].Beijing:National Defense Industry Press,1988.
[5] 石来德.机械的有限寿命设计和实验[M].上海:同济大学出版社,1992.
SHI L D.Mechanical finite life design & experiment[M].Shanghai:Tongji University Press,1992.
