海上浮式集装箱起重机非线性动力学模型及试验验证
2017-03-23孙友刚董达善李万莉强海燕刘玮杰
孙友刚,董达善,李万莉,强海燕,刘玮杰
(1.上海海事大学 物流工程学院,上海 201306; 2.同济大学 机械与能源工程学院,上海 201804)
集装箱起重机被广泛地应用于港口、码头和堆场的集装箱装卸[1].近年来,随着全球物流业的高速发展和运输成本竞争的日益激烈,集装箱运输船的尺寸不断增大.目前,已经有超过12 000 TEU级别的集装箱运输船在主航线上使用,并且更大级别的超过15 000 TEU的集装箱船已经交付客户.预计到2020年,超大型18 000 TEU的集装箱运输船将会在海上运行.因此,为了配合越来越大的运输船尺寸,集装箱起重机变得更大、更快和更高,这也使得起重机控制系统要满足快速装卸要求和严格的安全要求.除了这些提高以外,小型的集装箱码头和港口出现了新的问题:因为它们的水深相对较浅,大型的集装箱运输船无法靠岸过驳.为了解决这一问题,一种能在外海域作业的新型浮式集装箱起重机系统(又称“移动式港口”)被提出[2-4].图1为浮式集装箱起重机在外海上从大型集装箱运输船上装卸集装箱.
浮式集装箱起重机系统(又称“海上移动式港口”)这一概念起源于美国为军事行动而设计的可以移动的海上集装箱码头.2005年由荷兰代尔夫特理工大学的Beemen[5]设计的大型浮式集装箱起重机在鹿特丹港口服役,引起世界的广泛关注.韩国科学技术院主导设计的近海浮式集装箱起重A1-250在2012年丽水世界博览会上展出.在国内,为提高内河斜坡式港口的装卸效率,我国已在2003年开发了5 t内河浮式双悬臂桥式起重机[6].2004年,交通部水运科学研究院在《提高现有集装箱码头装卸效率》报告中,将浮式集装箱起重机列为未来重点发展机遇[7].上海振华重工(集团)股份有限公司也提出了浮式平台作业方案,并拟通过改造20万t级油轮进行论证.但是目前仍然缺少针对大干扰海上作业环境的非线性动力学机理研究.

图1 浮式集装箱起重机在海上装卸作业Fig.1 Offshore container crane handling operation at sea
在集装箱装卸的过程中,小车的运动和波浪引起的船体运动都会导致吊运的集装箱摆动.这不仅会引起潜在的安全事故,还会大大增加精确定位集装箱的时间.因此,必须设计高效的防摇控制策略.在设计控制系统之前,波浪作用下的集装箱起重机的动力学模型必须清晰.设计浮式起重机控制系统的第一步是分析对象的动力学特性.
集装箱(吊重)由4绳吊具悬挂在空中.根据不同的研究角度和目的,集装箱起重机能通过许多不同的方法建模.当看作集中参数系统时,吊重的摇摆被建立成单摆运动[8-10].当看作分布式参数系统时,吊绳当作柔性体被研究[11-13].岸边集装箱起重机的动力学也一直被研究[8,14].海上的起重机研究比较多的是浮吊系统[10,12,15].但浮吊的回转式和集装箱起重机的桥式结构有本质区别.除此之外,海洋结构物和波浪的相互作用也是研究热点[16]
本文针对浮式集装箱起重机,在非惯性坐标系中采用Lagrange法推导动力学方程.提出的动力学方程不但描述小车控制力以及小车运动对系统状态的影响,并且充分考虑波浪作用产生的船体运动对系统状态的影响.通过仿真和试验,证明了所提出的动力学模型的有效性.该模型可用于动力学特性分析,也可为控制器的设计提供数学对象.
1 模型假设
浮式集装箱起重机的船体在波浪作用下的运动非常复杂.如图2所示,船体存在6自由度运动,分别是3个平移运动(横荡、纵荡、升沉)和3个旋转运动(横摇、纵摇、艏摇).然而,本文只考虑3个运动,分别是升沉、横摇和纵摇.这样简化是因为移动式港口通过特殊的对接机构连接到母船(大型集装箱运输船),而具有巨型尺寸的母船可以被认为是在海里静止的[17-19].根据Fossen[17]提出的符号,船体的广义坐标可表示为
η=[0,0,z,φ,ψ,0]T
式中:z,φ,ψ分别为船体的升沉位移、横摇角度和纵摇角度.
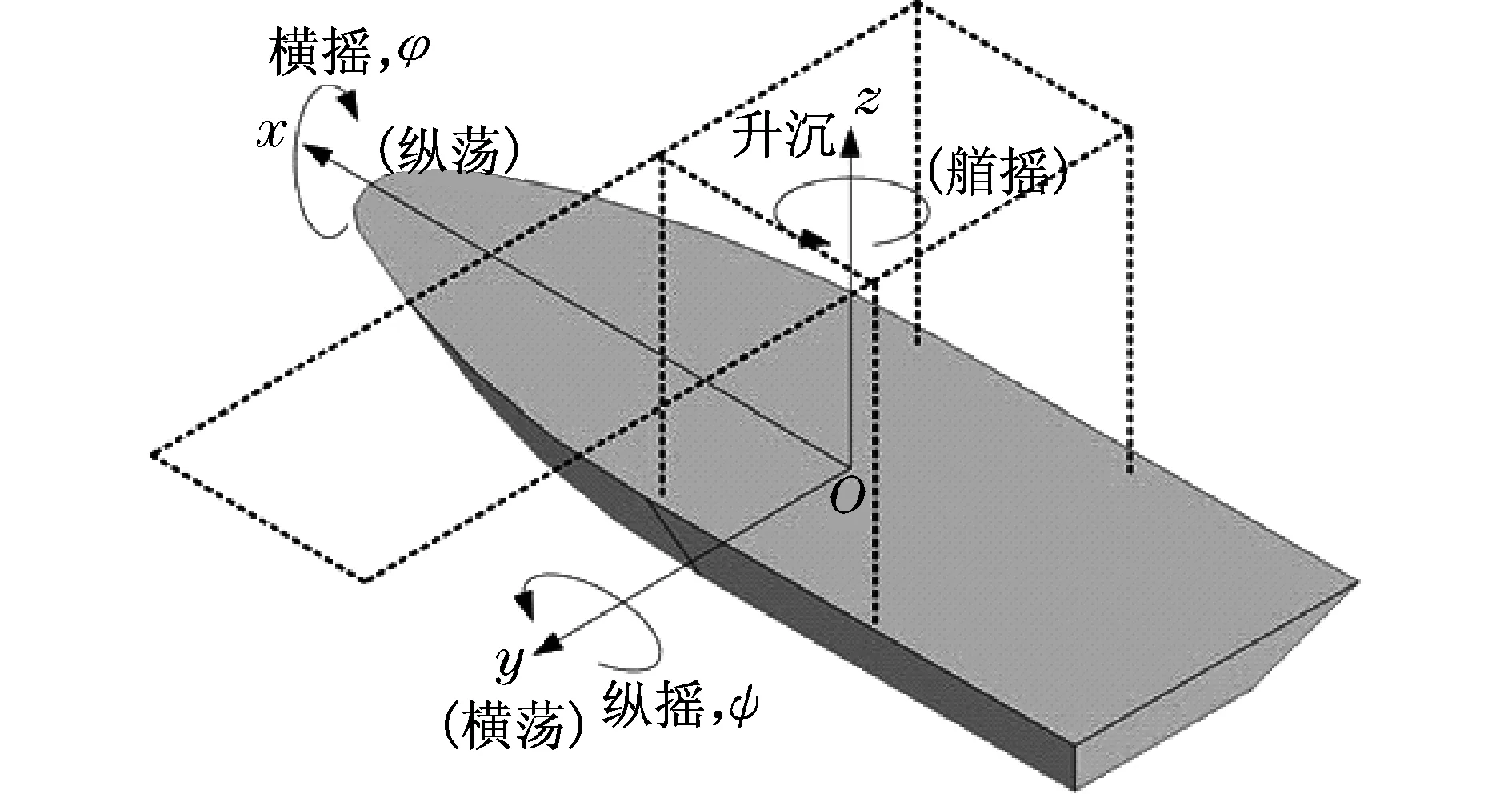
图2 移动式港口基座的运动Fig.2 Movement of mobile harbor
为了分析问题本质,给出如下假设:
(1) 将小车和集装箱吊重作为无体积的质点;
(2) 在小车运动过程中,假定驱动力fy即为牵引钢丝绳的合力;
(3) 忽略钢丝绳的质量且绳索刚度足够大;
(4) 不计风力和空气阻尼及系统弹性形变.
2 齐次坐标变换
对浮式集装箱起重机系统建立坐标系如图3所示.
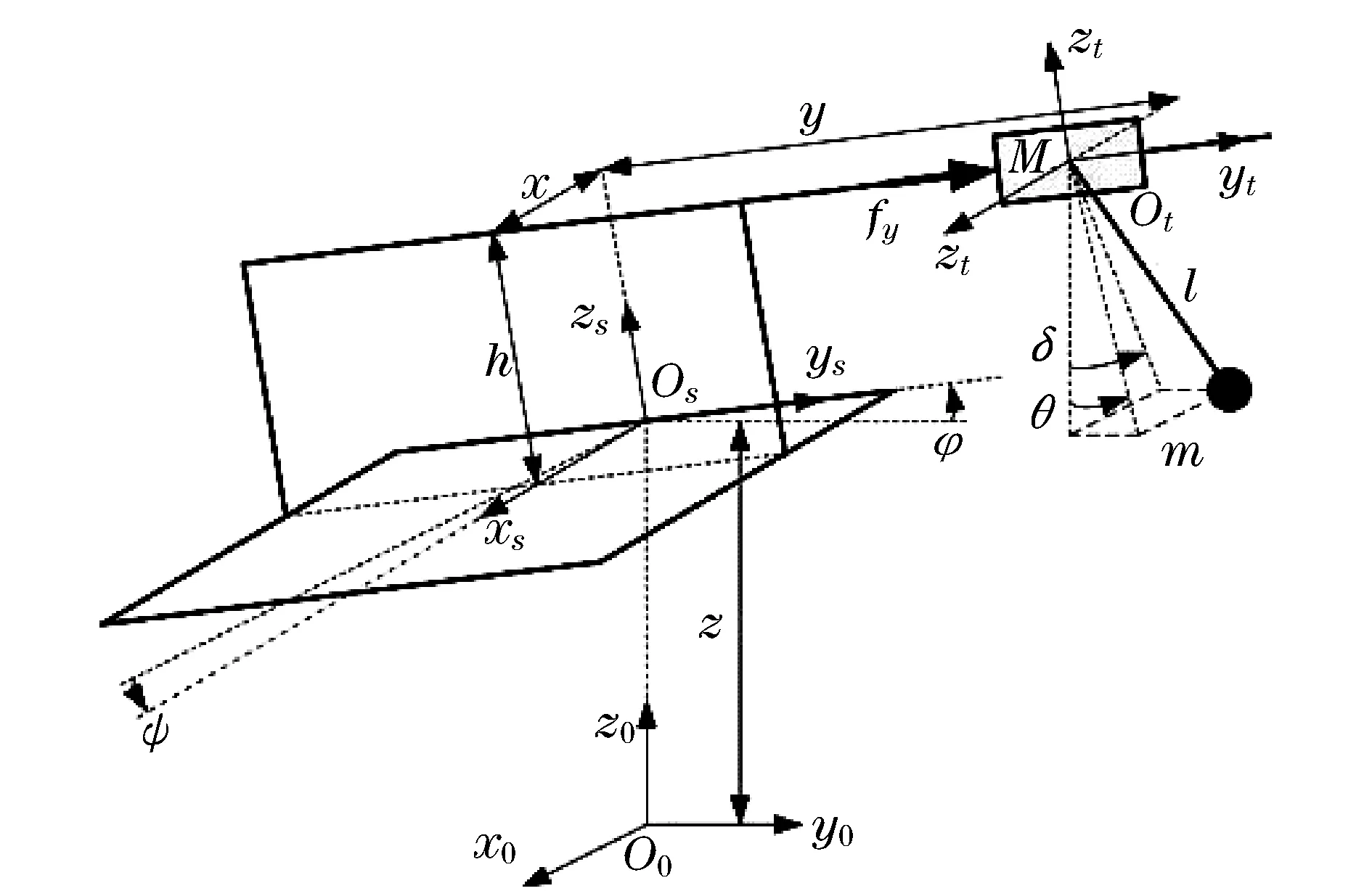
图3 坐标系统Fig.3 The coordinate system
图3中的各坐标系定义如下:
空间固定坐标系(O0-x0y0z0),又称惯性坐标系,是与地球固定的坐标系,也称为定坐标系.O0是任意选定、固定于地球表面的坐标系原点,坐标面O0x0y0在静水平面内.x0轴在船体的中性面内且平行于静水面,把指向船首的方向设为正方向,垂直平面O0x0y0竖直向上设为z0轴正方向.
随船移动的随动坐标系(Os-xsyszs)与(O0-x0y0z0)坐标系方向定义一致,原点设在船与起重机固定的平面上.小车随动坐标系(Ot-xtytzt)以小车中心为原点,小车沿导轨运动方向设为yt轴方向,与之垂直方向为xt轴指向.Os-xsyszs和Ot-xtytzt都是非惯性坐标系.
M和m点分别为小车和吊重(集装箱)简化成的质点,h为起重机门架高度,x和y为起重机小车在Osxsyszs参考坐标系中的坐标位置,l为吊绳长度,θ,δ分别为吊重在小车运行方向上摆动的面内角和面外角,fy为对小车施加的作用力.
船体的运动状态向量定义为(z,φ,ψ).从船体随动坐标系到惯性坐标系的齐次变换矩阵为
(1)
式中:
3 非线性动力学建模
3.1 小车及吊重的位移和速度
由图3对系统进行受力分析,小车位移pM和吊重位移pm分别为
(2)
(3)
对小车和吊重位移关于时间微分,小车和吊重的速度为


(4)
式中:



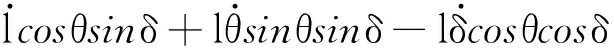


3.2 系统的动能和势能
(5)
U=Mg(z-xsinψ+ycosψsinφ+hcosψcosφ)+
mg(z-xsinψ+ycosψsinφ+hcosψcosφ)-
mglcosθcosδ
(6)
式中:g为重力加速度.需要指出的是本文对船的动能和势能不做讨论,船体运动视为对控制目标的干扰.
3.3 系统的拉格朗日算子
将q=(y,θ,δ)当作广义坐标,系统广义力为f=(fy,0,0).运用拉格朗日方程:
(7)
得到浮式集装箱起重机的船体-小车-吊重系统动力学方程如下:


(8)

(9)
(10)
式中:
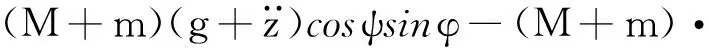
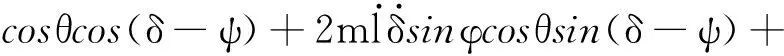







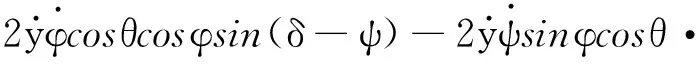



从这个数学模型上看,它的输入只有一个变量是驱动力fy,输出是两个变量,一个是吊重摆角θ,另一个是小车水平位移y,故为一个欠驱动系统,由于其中含有非线性项,所以是一个非线性二阶系统.
4 试验验证
4.1 试验装置
为了验证提出的动力学模型的正确性和精确度,需要通过一系列试验来评估.因为很难建立真实海浪干扰下的全尺寸浮式集装箱起重机实物,所以在实验室环境下搭建小型试验装置,总体结构如图4所示.试验系统包括三维起重机主体、6自由度运动平台、摆角及位移传感器(编码器)、伺服驱动系统、计算机及控制箱等.

图4 试验系统总体结构图Fig.4 Overall structure of the test system
如图5所示,6自由度运动平台用来模拟波浪作用下的船舶运动,三维起重机用来模拟缩比的集装箱起重机样机.实验平台的物理参数如下:起重机高度h=1.5 m,小车质量M=16 kg,吊重质量m=4 kg,吊绳长度l=0.7 m.
选取平台的运动(z,φ,ψ)分别如图6~图8所示.
4.2 试验结果及仿真对比
在Matlab环境中,基于Runge-Kutta法对本文提出的浮式集装箱起重机非线性动力学方程(8)~(10)进行理论数值求解.相关系统参数设置和试验样机保持一致.为了体现小车运动和吊重摆振的动力学耦合效果,关闭小车的刹车系统,使得小车和吊重保持自由运动.波浪的激励采用图6~图8所示的平台运动(z,φ,ψ).根据本文提出的动力学模型,面内摆角θ和面外角δ理论上的数字仿真结果如图9和图10中的实线所示.
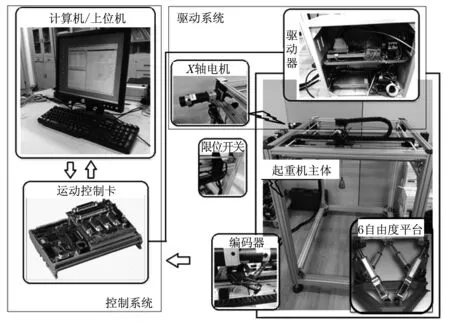
图5 试验平台实物系统Fig.5 Test platform system

图6 平台升沉运动z(m)Fig.6 Heaving movement of platform z(m)

图7 平台横摇运动φ(rad)Fig.7 Rolling motion of platform φ(rad)

图8 平台纵摇运动ψ(rad)Fig.8 Pitching motion of platform ψ(rad)
在搭建的试验平台中进行试验,6自由度平台的运动仅选取(0,0,z,φ,ψ,0)T,如图6~图8所示.用编码器测得的摆角试验结果如图9和图10中的虚线所示.理论仿真的结果和试验结果的误差如图11所示.
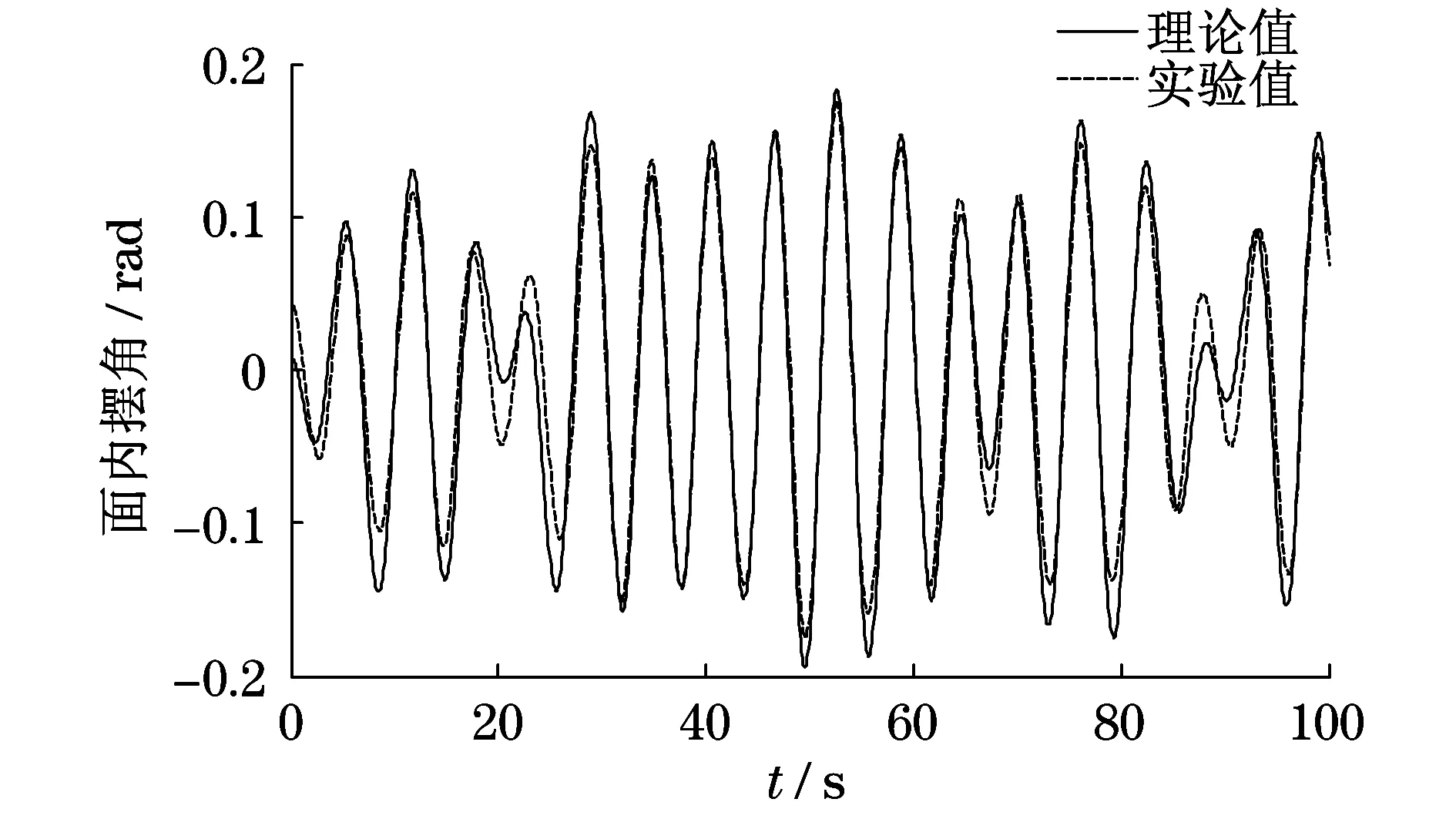
图9 理论仿真和试验结果对比(面内摆角θ)Fig.9 Comparison of the simulation and test results (angle θ in plane)

图10 理论仿真和试验结果对比(面外摆角δ)Fig.10 Comparison of the simulation and test results (outside angle δ)
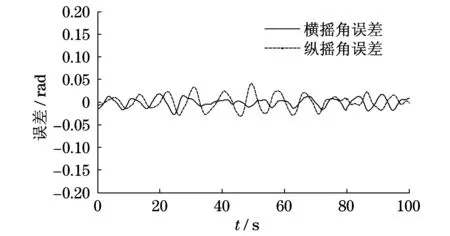
图11 理论仿真和试验结果误差Fig.11 Error between theoretical simulation and test results
5 结论
本文研究了浮式集装箱起重机的动力学模型,模型包括波浪引起的船体运动和船体运动引起的吊重摆振.采用Lagrange法推导了小车和吊重的运动方程,最后搭建试验平台进行试验验证.对比理论仿真和试验结果,可得出以下结论:
(1) 吊重摆角(面内角、面外角)的仿真结果和试验结果相当接近.这验证了本文所推导的非线性动力学方程组的有效性.
(2) 吊重的面内和面外摆角幅值较大,已经会影响到集装箱的对箱操作,需要对吊重进行防摇控制.面内摆角和小车运动方向共面,可以采用传统的控制小车的行走轨迹法来起到消摆的效果.
(3) 因为吊重的面外摆角方向和小车行走方向不共面,传统的防摇控制策略将会失效,面外摆角的防摇成为亟待解决的关键问题.课题组之后的工作将考虑开发侧向防摇机构.
[1] 董达善.港口起重机[M].上海:上海交通大学出版社,2014.
DONG D S.The port crane[M].Shanghai:Shanghai Jiao Tong University Press,2014.
[2] KIM J H,MORRISON J R.Offshore port service concepts:classification and economic feasibility[J].Flexible Services and Manufacturing Journal,2012,24:214-245.
[3] BAIRD A J,ROTHER D.Technical and economic evaluation of the floating container storage and transhipment terminal(FCSTT)[J].Transportation Research Part C-Emerging Technologies,2013,30:178-192.
[4] JANG I G,KIM K S,KWAK B M.Conceptual and basic designs of the mobile harbor crane based ontopology and shape optimization[J].Structural and Multidisciplinary Optimization,2014,50:505-515.
[5] 张荣忠.浮式集装箱起重机[J].港口装卸,2006(6):5-6.
ZHANG R Z.Floating container crane[J].Port Operation,2006(6):5-6.
[6] 郑见粹,杨建中.适用于斜坡式码头的浮式桥式集装箱起重机[J].水运科学研究,2006(4):28-32.
ZHENG J C,YANG J Z.Quay-side floating container crane for inland river terminals with slopping wharf[J].Research on Waterborne Transportation,2006(4):28-32.
[7] 彭传圣.浮式桥式集装箱起重机船岸作业系统效率分析[J].港口装卸,2005(5):13-18.
PENG C S.Efficiency analysis of shore operation system of floating bridge container crane[J].Port Operation,2005(5):13-18.
[8] KIM C S,HONG K S.Boundary control of container crane from the perspective of controlling an axially moving string system[J].International Journal of Control,Automation and Systems,2009,7(3):437-445.
[9] 孙友刚,李万莉,刘祥勇.海上浮吊平台作业的波浪补偿系统的仿真与研究[J].中国工程机械学报,2016,14(3):198-205.
SUN Y G,LI W L,LIU X Y.Simulation on heave compensation system for floating cranes during offshore operation[J].Chinese Journal of Construction Machinery,2016,14(3):198-205.
[10] 董达善,孙友刚,刘龙.浮吊海上补给作业的动态特性仿真分析与研究[J].科学技术与工程,2013,20:5872-5877.
DONG D S,SUN Y G,LIU L.Simulation studies on dynamic characters of floating cranes[J].Science Technology and Engineering,2013,20:5872-5877.
[11] ANDREA-NOVEL B,CORON J M.Exponential stabilization of an overhead crane with flexible cable via a back-stepping approach[J].Automatica,2000,36(4):587-593.
[12] 董达善,孙友刚,刘龙,等.基于虚拟样机技术的浮吊补给作业动态特性仿真研究[J].机械科学与技术,2015(3):393-397.
DONG D S,SUN Y G,LIU L,et al.Simulation study on dynamic characters of floating crane based on virtual prototype technology[J].Mechanical Science and Technology for Aerospace Engineering,2015(3):393-397.
[13] 董达善,孙友刚,刘龙.基于虚拟样机技术的钢丝绳动张力仿真研究[J].机床与液压,2013,17:156-162.
DONG D S,SUN Y G,LIU L.Study on dynamic tension of wire rope based on virtual prototype technology[J].Machine Tools and Hydraulic,2013,17:156-162.
[14] 张纪元,钟怀茂.岸边集装箱起重机起升动载系数的动力学模型及其解[J].上海海事大学学报,2006,27(2):12-16.
ZHANG J Y,ZHONG H M.Container crane uprising dynamic load coefficient dynamics model and its solution[J].Journal of Shanghai Maritime University,2006,27(2):12-16.
[15] SUN Y G,LI W L,DONG D S,et al.Dynamics analysis and active control of a floating crane[J].Technical Gazette,2015,22(6):1383-1391.
[16] 刘龙,董达善,沈佳辉,等.深海张力腿非线性动力学分析[J].船舶工程,2015,37(8):94-97.
LIU L,DONG D S,SHEN J H,et al.Nonlinear dynamic analysis of vortex-induced vibration of tension leg platform in deep sea[J].Ship Engineering,2015,37(8):94-97.
[17] FOSSEN T I.Guidance and control of ocean vehicles[M].New York:John Wiley & Sons,1994.
[18] NEYES M A S,RODRIGUEZ C A.On unstable ship motions resulting from strong non-linear coupling[J].Ocean Engineering,2006,33(14/15):1853-1883.
[19] SELYAM R P,BHATTACHARYYA S K.System identification of coupled heave-pitch motion of ships with forward speed in random ocean waves[J].Ships and Offshore Structures,2010,5(1):33-49.
