基于四元数法的运动平台红外图像旋转角推导
2017-03-22侃1石永彪1
吕 波,张 涌,黄 侃1,,石永彪1,
基于四元数法的运动平台红外图像旋转角推导
吕 波1,2,3,张 涌2,黄 侃1,2,石永彪1,2
(1.中国科学院大学,北京 100049;2.中国科学院上海技术物理研究所,上海 200083;3.中国科学院红外探测器与成像技术重点实验室,上海 200083)
在电子稳像领域,传统求取图像的旋转角是从连续帧图像序列中提取相关信息计算的,其缺点是计算量大、实时性不高等。本文在惯导模块给出的航向角、横滚角和纵倾角3个姿态角以及伺服模块给出的方位角和俯仰角两个角度的基础上,利用四元数法,结合空间解析几何知识,推导出图像旋转角。通过车载运动平台线列图像的验证实验表明,旋转角的推导正确,图像经矫正后起到了电子稳像的效果。
车载运动平台;红外图像;四元数
0 引言
在捷联式惯导系统中,安装在车载、舰载和机载等运动平台上的红外成像设备由于平台的晃动,导致光学成像器件相对平台的运动,最终使红外图像发生旋转,这部分旋转量给观察及操作人员带来视觉不便甚至带来错误的判断,所以对目标图像需要进行消旋[1-2]。在纯电子消旋技术中传统做法是从连续帧图像序列中提取相关信息求取旋转角度[3],其缺点在于计算量大,实时性不高等。
本文根据船摇的航向角、横滚角和纵倾角以及光电跟踪设备的方位角和俯仰角这5个角度,在刚体运动物理模型的基础上计算出图像的旋转角度。与传统的欧拉角相比,四元数对姿态转动的描述更简洁,并且具有计算速度快、精度高、非奇异的优点,使其在许多领域得到了广泛的应用[4]。本文即在四元数的基础上结合空间解析几何知识推导出旋转角度。对于红外视频图像在计算出旋转角度后通过图像处理几何校正,可以起到电子稳像的效果。
1 四元数方法描述
一个四元数是一个标量分量和一个3D向量分量构成的超复数[5]:




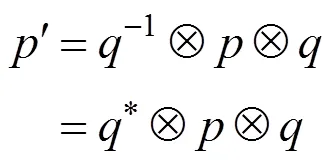

(4)式表明一个向量多次旋转等价于多个旋转变量乘积后的单一旋转[7]。
2 坐标系的设定与主要角度说明
方便旋转角度的推导,设定以下坐标系,如图1所示。

图1 坐标系定义
1)大地坐标系:X轴指向正东,Y轴指向正北,Z轴指向天空,构成右手系。
2)运动平台坐标系:Y为轴运动平台前进方向,Z轴垂直平台指向平台上方,X轴遵循右手系指向,初始与大地参考坐标系重合。
3)视场视轴坐标系:定义成像设备视轴作为Y轴,X轴和Z轴构成视场,遵循右手系,初始与运动平台坐标系重合。
航向角为运动平台前进方向绕Z轴旋转的角度,逆时针为正角度;横滚角为运动平台绕Y轴旋转的角度,X轴正方向向下为正角度;纵倾角为运动平台绕X轴旋转的角度,Y轴正方向向上为正角度。
方位角是光电经纬仪方位轴转动使视轴与Y正方向之间的角度,逆时针为正角度;俯仰角是光电经纬仪俯仰轴转动使视轴与运动平面之间的角度,视轴正方向向上为正角度。
3 红外运动图像旋转角的四元数推导
3.1 视场旋转角的定义
由于图像的旋转是视场成像相对运动产生的,所以旋转角度应该在大地坐标系下定义。如图2所示,矩形为视场,直线为视场与大地坐标系水平面XOY的相交直线,旋转角即为视场X轴与直线之间的夹角。

图2 旋转角q的定义
3.2 旋转角度的求解
推导旋转角的步骤如下:

2)系是方位轴和俯仰轴相对系转动得到的[8]。由四元数知识,系到系的旋转为沿X轴旋转―,再沿Z轴旋转―,因此,表示由系到系的四元数为:

3)系是运动平台相对系转动得到的。由四元数知识,系到系的旋转为沿Y轴旋转―,再沿X轴旋转―,最后沿B轴旋转―,因此,表示由系到系的四元数为:
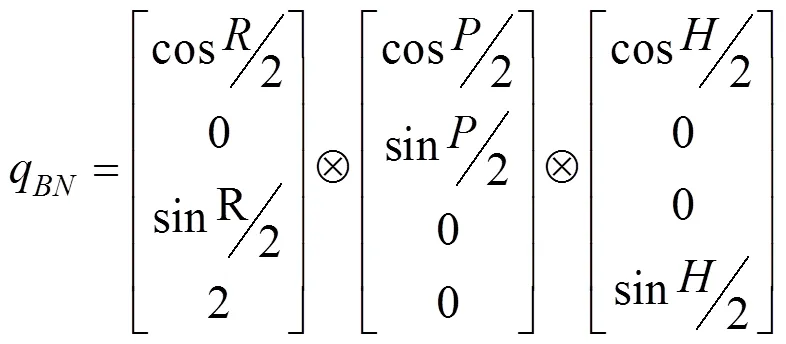
4)根据公式(4),多次旋转时可转化为一次旋转,系旋转至系,然后系旋转至系,可直接看成系旋转至系:
q=qÄ q(7)

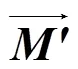



视场平面和水平面的相交直线一般方程:

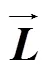

4 四元数求解旋转角验证实验
为验证本文算法推导的正确性,选择某车载红外告警项目的红外图像进行测试。红外成像设备进行360°旋转扫描,形成一幅二维全景图像。数据格式保存在研究室自定义的视频文件里,该文件由文件头和图像数据组成,文件头包括每列图像的3个惯导角度数据、方位角和俯仰角。对图像数据处理采用Matlab进行编程[10],读入视频文件后,提取文件头中的5个角度并计算出旋转角度,最后利用旋转角度,结合灰度值插值矫正图像,输出到显示设备显示。
图3~图7为抽取的某帧部分图像并提取其航向角、纵倾角、横滚角3个姿态角和方位角、俯仰角两个伺服模块采集的角度。图3为成像设备的红外探测器进行了0°~360°的旋转,形成一条直线;图4是在伺服模块控制下,红外探测器做-1.8°~2.5°范围内的俯仰制动,呈现正余弦状态;从图5、图6和图7来看,鉴于车载实验选择路面凹凸度不是很大,3个姿态角变化幅度变化缓慢,航向角变化范围为84.5°~88.5°之间,纵倾角变化范围为0.47°~0.53°之间,横滚角变化范围为1.96°~2.14°之间。即便车载运动平台没有剧烈运动,但在对图像没有矫正前,显示设备的视频图像总是在不断晃动。经前文所述方法计算后,其旋转角度如图8所示,范围在±2.2°内微动,呈现余弦状。

图3 方位角
Fig.3 Azimuth angle

图4 俯仰角
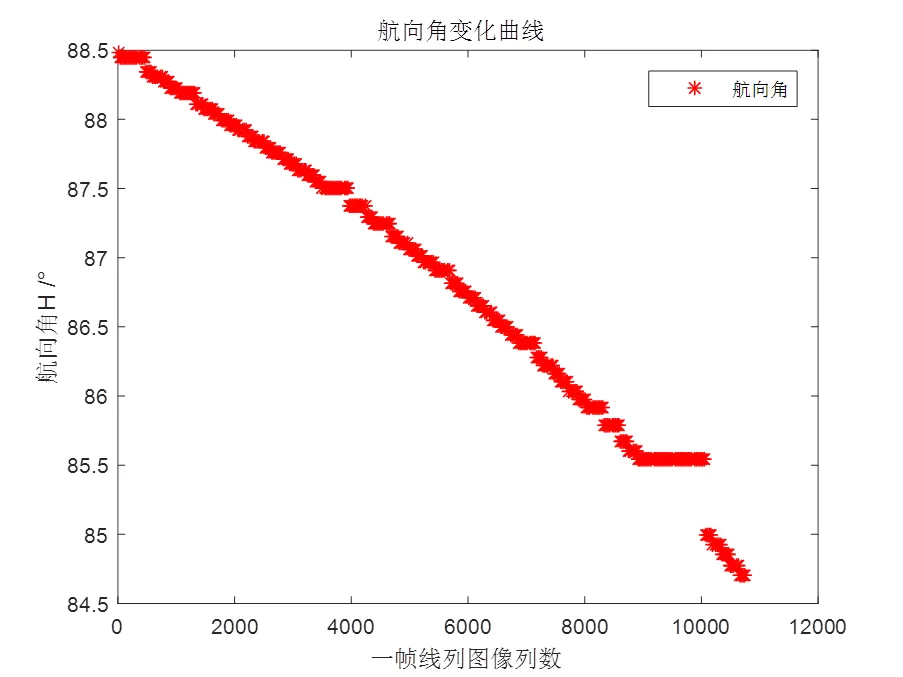
图5 航向角
Fig.5 Heading angle

图6 纵倾角

图7 横滚角

图8 旋转角度
图9是红外探测器扫描的连续5幅图像,截取大小为287×502,5幅图像的平均旋转角度依次为-0.8426°、-0.9391°、-0.8579°、-0.6951°、-0.8694°,选取双三次插值法灰度插值。其中图9的(a)、(c)、(e)、(g)、(i)为5幅原始图像,(b)、(d)、(f)、(h)、(j)为矫正后的图像,该矫正图像经过截取等处理后即可传输到显示设备显示。实验结果表明,该方法在视觉效果上得到了显著改观。

5 总结
本文在车载、舰载或机载等运动平台项目背景下,由于平台晃动致使红外图像发生了旋转,造成观察上不适以及给后续的图像处理造成了困扰,故提出了利用四元数法结合空间解析几何知识的方法,计算出红外图像产生的旋转角度,并再此基础上进行图像的旋转矫正,起到了电子稳像的效果。经实验验证,达到了预期目标。
[1] 孙莹涛. 船载实时图像消旋系统设计[D]. 西安: 西安电子科技大学, 2007.
SUN Yingtao. The Design of Real-time Image Rotation-elimination System Used on Ships[D]. Xi'an : Xidian University, 2007.
[2] 高宏昌. 机载电光跟踪系统图像消旋原理研究[J]. 电光与控制, 1995, 59(3):14-24.
GAO Hongchang. Study on the principle of image rotation elimination of airborne photoelectric tracking system[J]., 1995, 59(3): 14-24.
[3] 张浩钧. 红外系统中电子复原、稳像及嵌入式成像系统关键技术研究[D]. 上海: 中国科学院上海技术物理研究所, 2012.
ZHANG Haojun. Research on Key Technologies for Infrared Image Restoration, Video Stabilization and Imaging System Based on Embedded System[D]. Shanghai: The Shanghai Institute of Technical Physics(SITP) of the Chinese Academy of Sciences, 2012.
[4] 周江华, 苗育红, 李宏, 等. 四元数在刚体姿态仿真中的应用研究[J]. 飞行力学, 2000, 18(4): 28-32.
ZHOU Jianghua, MIAO Yuhong, LI Hong. Research of attitude simulation using quaternion[J]., 2000, 18(4): 28-32.
[5] 秦永元. 惯性导航[M]. 北京: 科学出版社, 2006.
QIN Yongyuan.[M]. Beijing: science press, 2006.
[6] 陈志明, 王惠南, 刘海颖. 全角度欧拉角与四元数转换研究[EB/OL]. [2006-11-09] http: //www. paper.edu.cn/ releasepaper/ content/200611-221.
CHEN Zhinming, WANG Huinan, LIU Haiying. Research on Large-scale Transformation Algorithm of Quaternion to Euler Angle[EB/OL]. [2006-11-09] http: //www. paper.edu.cn/ releasepaper/ content/200611-221.
[7] Fletcher Dunn, Ian Parberry. 3[M]. 2002: 147-193.
[8] 吕舒, 张涯辉, 包启亮, 等. 舰载光电跟踪系统视场消旋方法研究[J]. 中国激光, 2014: 042303-1-042303-6.
LV Shu, ZHANG Yahui, BAO Qiliang. Despinning scheme of shipboard electro-optical tracking system[J]., 2014: 042303-1-042303-6.
[9] 同济大学应用数学系. 高等数学[M]. 北京: 高等教育出版社, 2002.
Department of Applied Mathematics, Tongji University.[M]. Beijing: Higher Education Press, 2002.
[10] 刘卫国. MATLAB程序设计与应用: 第二版[M]. 北京: 高等教育出版社, 2006.
LIU Weiguo.: second edition[M] .Beijing: Higher Education Press, 2006.
The Derivation of Rotation Angle of Infrared Image in Moving Platform Based on Quaternion
LV Bo1,2,3,ZHANG Yong2,HUANG Kan1,2,SHI Yongbiao1,2
(1.University of Chinese Academy of Sciences, Beijing 100049, China; 2.Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai 200083, China; 3.Key Laboratory of Infrared System Detection and Imaging Technology, Chinese Academy of Sciences, Shanghai 200083, China)
In the field of electronic image stabilization, the traditional method of calculating the rotation angle of image is calculating by extracting the relevant information from the sequence of consecutive frames. The disadvantage is large calculation quantity and poor real-time ability. The inertial navigation module got the heading angle, roll angle and pitch angle and the servo module gotazimuth angle and elevation angle. Based on the five angles, the image rotation angle is derived by utilizing the quaternion and space analytic geometry. Through calculating the rotation angle of the linear images of vehicle moving platform shows that the derived rotation angle is correct, which plays a role in electronic image stabilization.
vehicle moving platform,infrared image,quaternion
TP391
A
1001-8891(2017)04-0353-05
2016-10-02;
2016-12-06.
吕波,男(1984-),男,博士研究生,主要研究方向:红外图像处理、FPGA和DSP开发等,E-mail:lvbo5167@sina.com。
国家“十二五”国防预研项目。
