基于多尺度自相似性和非局部均值的单幅图像超分辨率方法
2017-03-22黄世奇
刘 哲,黄世奇,姜 杰
基于多尺度自相似性和非局部均值的单幅图像超分辨率方法
刘 哲,黄世奇,姜 杰
(西京学院信息工程学院,陕西 西安 710123)
提出了一种基于多尺度局部自相似性和非局部均值的单幅图像超分辨率算法,该算法不依赖于外界图像,仅仅在原始图像的局部子窗口中搜索目标图像块的相似子块,利用非局部均值算法对相似子块进行加权求和来估计待复原图像,然后在复原图像上叠加最相似子块的高频细节图像,获得高分辨率图像。实验结果表明,本文算法不仅能很好地重构图像的高频细节,还能很好地恢复图像的纹理特征。
超分辨率;多尺度;局部自相似;非局部均值
0 引言
这些年,随着图像超分辨率技术的快速发展,使得实现低成本、高分辨率、高信噪比的图像设备成为可能。图像超分辨率技术,是指用图像处理算法将低分辨率图像转换成高分辨率图像,构建更高分辨率图像所缺失的高频细节。高分辨率意味着图像中的像素密度高,能够提供更多的细节,而这些细节在许多实际应用中不可或缺。图像超分辨率技术在医学诊断、模式识别、视频监控、生物鉴别、高清晰电视成像、遥感图像解译、高空对地观测等领域有着广泛的应用。一直以来,图像超分辨率技术是视频图像处理领域研究的热门方向和一个具有相当挑战性的理论分支[1]。
传统的图像超分辨率技术有基于插值的超分辨率重建、基于重建的图像超分辨方法和基于学习的超分辨率算法[2]。近年来,随着图像局部自相似性和非局部均匀理论[3-6]的出现,局部自相似性和非局部均匀理论在图像增强、图像降噪和图像复原等方面得到了很好的应用,尤其是在在图像超分辨率方面取得了比其它方法更好的效果。基于图像局部自相似性的超分辨率方法利用了图像广泛具有的局部自相似性,并将这种结构自相似性作为图像重构过程中的附加信息[3-6]。近年来相继出现了一些利用非局部(nonlocal, NL)自相似结构的超分辨率方法[3-4],其基本思路是在整幅图像中搜索相同尺度的相似图像块,利用这些相似图像块所提供的互补信息重构高分辨率图像。由于图像自身中相同尺度相似图像块所提供的附加信息具有一定的局限性,因而制约了这种方法图像重构效果的进一步提升,文献[5]构建与图像高、低频子图所对应的高、低频码本,并通过高频码本所提供的附加信息实现图像重构,这种方法实际上是利用了图像自身不同尺度相似图像块所提供的附加信息。文献[6]将相同尺度和不同尺度相似图像块所提供的附加信息均加入到图像重构过程中,利用相同尺度相似图像块就如同利用多幅低分辨率图像,而不同尺度相似图像块又提供了不同分辨率图像块间的对应关系,取得了良好图像重构效果和视觉效果。Freedman等[7]使用简单的灰度信息作为特征,使得复原效果提升有限。文献[8-11]使用稀疏表示技术,通过自相似性建立冗余字典或典书(codebook)进行超分辨率复原,取得不错的效果,但是该算法复杂度较大;Glasner等[12]由输入图像采用金字塔的形式构建训练库,利用图像块的冗余度并结合传统超分辨算法和基于样本的超分辨率算法,得到了较好的算法结果,但是算法容易产生人工痕迹。
针对传统插值超采样算法和相关的基于学习的超分辨率算法的缺陷[13-15,16-18],在考察了局部自相似性学习的超采样方法各自的优势后,本文针对单幅图像超分辨率重建问题,提出了一种基于多尺度局部自相似单幅和非局部均值单幅图像超分辨率方法。首先,给出了本文提出的“类高斯”引导滤波器技术,该滤波器具有良好的图像边缘保持和图像平滑降噪能力;其次利用该引导滤波器与该图像卷积求差,求出图像的高频细节图像HF(下文用HF表示高频细节图像);再次使用轮廓模板插值方法将原始图像放大倍,得到放大后的LR图像;接着,利用图像自身的局部自相似性,在LR图像上取一个小窗口,分别在原始图像和HF图像上对应的一个大窗口内,利用非局部均值(NLM)计算图像块间的相似重建系数,继而将此重建系数传递给对应原始图像中的图像块,通过相似块的加权平均来重建图像块的值;最后,将重建图像块和其对应最相似块的高频细节图像叠加,得到最终的超分辨率图像。重复这个过程,直至达到需要的放大倍数。
1 高频细节图像HF的求取
1.1 “类高斯”引导滤波器
引导滤波是近年才出现的滤波技术,在引导滤波的定义中,用到了局部线性模型。该模型认为,某函数上一点与其邻近部分的点成线性关系,一个复杂的函数就可以用很多局部的线性函数来表示,当需要求该函数上某一点的值时,只需计算所有包含该点的线性函数的值并进行平均即可。这种模型在表示非解析函数上非常有用。
同理,我们可以认为图像是一个二维函数,而且没法写出解析表达式,因此我们假设该函数的输出与输入在一个二维窗口内满足线性关系,我们构造如下函数:
q=aI+b(1)
式中:是输入图像;是输出图像;a和b的表达式为:
a=(I-)2/[+(I-)2]
b=-a(2)
式中:为满足0<<1的因子,用来控制a值的大小及函数宽度,同时避免a过大。
式(1)表示在以为中心的×方形区域内,输出图像和输入图像满足线性映射关系。×方形区域所有像素的均值用表示,其计算公式为:

式(1)~(3)组成了本文所提出的均值引导滤波器。下面对所给出的均值引导滤波器性质进行讨论:
1)Ñq=aÑI,即当输入图像有梯度时,输出图像也有类似的梯度,这就是可以解释均值滤波器具有边缘保持功能。
2)当I不是边缘点时,I的值趋近于时,即I®,此时a≈0,b≈,由此可得q=b,输出图像的像素点q被平滑。
3)当I是边缘点时,I的值和的值相差较大,此时a®0,b≈0,由此可得q=I,由此输出图像的像素点q的边缘点得以保持。
下面对函数a进行讨论,为了讨论方便,将I的归一化到[0,1]区间,此时=0.5。I在[0,1]区间内作为输入,a作为输出,分别画出=0.5、=0.1、=0.01、=0.05时a的图形,分别如图1所示。
由图1可知,函数a具有以下优良的性质:
1)该函数图形是“倒高斯分布图”,在本文中称作“类高斯核”,具有轴对称、各向同性,连续性、光滑性好。
2)它与图像卷积不会改变图像的整体动态特性。
3)当I®时,a®0;当I与差距越来越大时,a®1;所以该函数能自适应保持像素点的特性。
4)当尺度因子越来越小时,该函数宽度越来越小,函数变化越迅速;尺度因子越来越大时,该函数宽度越来越大,函数变化越缓慢;较大时,表现为平滑性越好,当较小时,表现为边缘保持性好。
5)具有与高斯函数相同的性质,可以做为核平滑函数,在图像处理领域可以得到广泛应用。
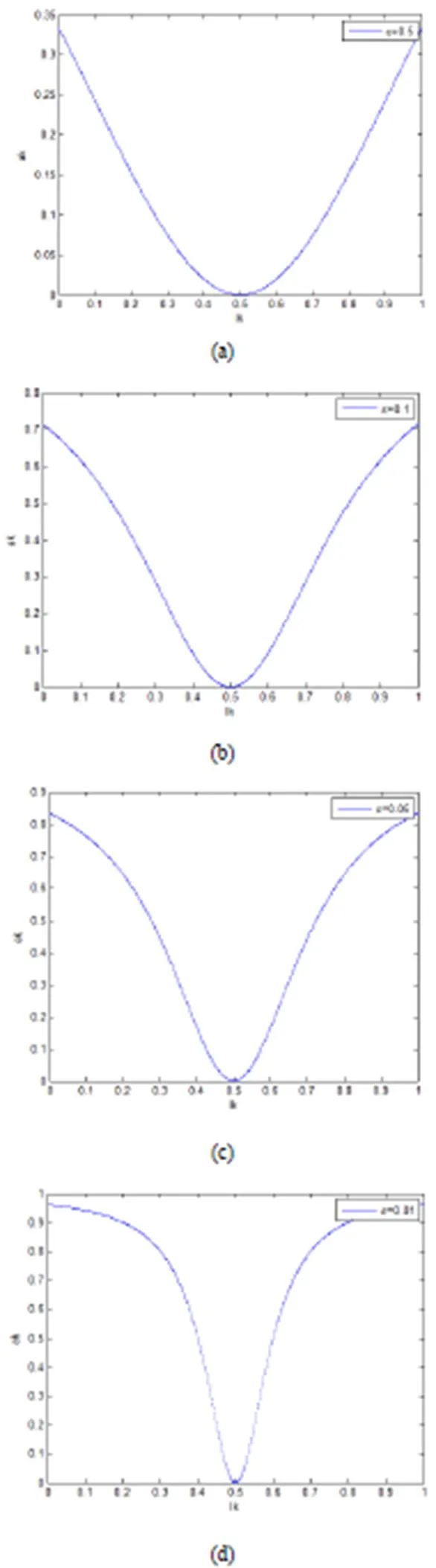
图1 当e取不同值时函数ak的图形
1.2 HF图像的求取
优异的图像超分辨率算法应该满足以下2个条件:
①能很好地恢复图像的高频细节部分;②能很好地恢复图像的局部纹理特征。
设输入图像为,是引导滤波器,则输入图像的高频细节图像HF计算如下:
HF=-*(4)
式中:*代表卷积;的尺寸选为5×5。
通过求HF,可以把隐藏在图像内部的高频信息给挖掘出来,如图2所示。图2左图是原始图像,右图是运用式(4)所求原始图像的高频细节图像。由图2可以看出,运用引导滤波器可以很好地获得图像丰富的边缘细节信息。

图2 高频细节图像求取结果
2 多尺度局部自相似超分辨率算法
2.1 基本思想
图像的局部自相似性是指在同一幅图像中存在相同尺度或不同尺度的相似结构,其具体表现为图像中相同尺度或不同尺度中位于局部邻域中的图像具有相似图像块。研究这种局部自相似性,提取这些相似块中的高频细节成分,进行分析处理和纹理细节合成,估计出高分辨率图像中的高频细节成分,以此实现图像的超分辨率。利用局部自相似性进行超分辨率重建的方法原理,训练集合包含3幅图像,分别是原始图像、原始图像对应的高频图像HF以及原始图像对应的插值放大图像LR。我们的目标是不依赖于任何外界图像,利用图像在不同尺度间的自相似性特征,生成超分辨率图像HR。
2.2 插值和块匹配搜索
对原始图像,首先采用插值算法将其放大倍得到初始高分辨率图像LR,插值算法的选取会对最终结果产生一定影响,一个较好的插值算法必然会得到一个较好的最终结果。选取Getreuer的轮廓模板插值算法[16]。算法利用高分辨率图像的轮廓与输入的低分辨率图像的轮廓保持一致的特性,事先估计自然图像轮廓的形状得到了具有57个轮廓模板的待选模板的集合。对于输入的低分辨率图像的每个像素点计算其为中心的邻域的轮廓模板值,选取合适的模板进行插值。最终得到了较好的高分辨率图像。轮廓模板插值算法在保持插值图像整体轮廓和细节等方面都取得了很好的效果,但是由于缺少先验知识,得到的高分辨率图像和自然图像相比,纹理部分有所缺失。本文进一步处理,补充高频的纹理细节部分。
在初始高分辨率图像LR中以像素(,)为中心,构造一个小窗口图像块作为待匹配窗,在中对应位置(,)为中心的一个大窗口邻域内搜索相似块,其中:
=/,=/(5)
式中:为缩放因子。
块匹配搜索如图3所示。图3的左侧代表插值放大后的图像LR,右图代表原始图像,在LR中选取大小为3×3的待匹配窗,在中选取大小为5×5的搜索窗,的中心坐标是(,),的中心坐标是(,),分别是图中黑框表示的像素坐标值。匹配窗在搜索窗内进行相似块的搜索,本文采用两个图像块对应点像素值之差的绝对值之和(sum of absolute difference, SAD)作为相似度的标识。

图3 块匹配搜索示意图
2.3 基于非局部均值的灰度图像自相似性重构
非局部均值滤波是一种基于块匹配来确定滤波权值的滤波算法,非局部均值滤波在计算中加入了每一个点的权重值,所以能够保证在相邻且相差很大的点在方框中求平均值时相互之间的影响减小,也就对图像边缘细节部分保留很多,这样图像看起来会更清晰,同时还能很好的抑制噪声。因此,首先进行基于非局部均值的灰度图像自相似性超分辨率重构。这样既保证了超分辨率重构图像大量边缘信息的保留,同时也抑制了噪声。


式中:()表示第个相似块p。权值()满足:

()可以表示为:
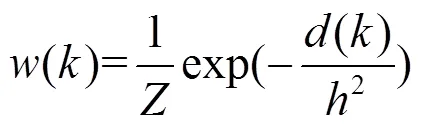
式中:()表示图像块与p之间的欧式距离;表示归一化常数。

于是根据式(9)可以求出归一化常数:

由上面的推导知道,利用式(6)可完成基于非局部均值的灰度图像自相似性的超分辨率重构。虽然利用这种方法进行超分辨率重构的图像能保留大部分边缘细节信息,但会使相当多的纹理特征损失。对于损失的纹理特征通过高频细节自相似性重构来进行恢复。
2.4 基于最佳匹配块的高频细节自相似性重构
下面利用图像自相似性,待匹配窗在搜索窗的邻域内进行匹配搜索,找到与最相似的匹配块,再在HF图像找到与最匹配块相对应的高频图像块h。本文中SAD作为相似度的标识,所以最匹配块就是SAD值最小的两个块。所以:
=argmin|-|(11)
根据式(4)可以求出最佳匹配块的高频图像块h:
h=-*0(12)


2.5 多尺度框架下超分辨率算法
在2.2节中,我们提到了用轮廓模板将原始图像放大倍,当这个取不同值时,最佳匹配块之间的SAD均值是否接近,这是我们进行多尺度设计的主要依据。为此,我们设计了一个实验,来说明尺度因子取不同值时,局部自相似性的效果。其中,匹配块的大小为3×3,搜索窗的大小为5×5,特征为RGB空间灰度值(0~255),并对SAD均值进行归一化。图4给出了放大因子取不同值时,SAD归一化均值的取值情况。

图4 放大因子a取不同值时SAD归一化均值
由图可知,随着放大因子的增大,SAD归一化均值也增大,即图像的局部自相似性变得越差,尤其是当逐步增大时,图像的局部自相似性急剧变差。所以我们设为放大尺度因子,它的取值可以比较小,通过逐步迭代把图像放大到需要的倍数。设为为每一次迭代时的尺度因子,为最终要达到的放大倍数,要达到放大倍数,需要迭代次:
=ln/ln(14)
这就是多尺度自相似性的主要原理。
由式(14)可以看出,当的取值过小,迭代次数过多,算法的时间复杂度就大大增加。当的取值逐步增大时,寻找到的匹配块相似度会下降很快。本文所处理的图像是放大到2倍,我们选取放大尺度因子的值为1.25,需要迭代4次就可以完成。
2.6 算法实现
基于引导滤波和多尺度局部自相似单幅图像超分辨率算法实现过程如下:
1)对原始图像,首先采用轮廓模板插值算法将其放大倍得到初始高分辨率图像LR。
2)将LR有重叠划分成3×3的子块,重叠区域宽度为1个像素,构成待匹配窗;将原始图像有重叠划分成5×5子块,重叠区域宽度为2个像素,构成搜索窗。

4)利用图像自相似性,待匹配窗在搜索窗的邻域内进行匹配搜索,找到与最相似的匹配块;利用式(12)求出最佳匹配块的高频细节图像块h。

6)合并所有的超分辨率重构的待匹配窗,相邻图像块重叠区域的像素值使用平均融合得到,得到最终的超分辨率图像HR。
7)令=HR,返回步骤1),直至得到最终放大倍数。
3 实验和分析
为了验证本文算法的有效性,将基于多尺度局部自相似性和非局部均值单幅图像超分辨率算法,与Freedman算法[7]、Glasner算法[12]进行综合分析比较。在所有实验中选取如下参数:
①放大尺度因子=1.25,通过4次迭代图像放大到2倍;②搜索窗的大小为5×5,匹配窗的大小为3×3;③引导滤波器的尺度因子=0.01。
测试环境为:①操作系统Windows XP SP3;②应用程序开发环境Matlab 2012a;③笔记本计算机配置Inter Core i5-Y430p,8.0GB内存。
3.1 高频细节对比分析
分别利用Freedman算法、Glasner算法和本文算法对图像进行2倍的超分辨率放大重构,分别如图5的(a)、(b)、(c)所示,而后利用本文提出的基于引导滤波算法,求取图像(a)~(c)的HF图像,其结果分别如图5的(d)~(f)所示。由图5可知,由本文超分辨重构图像的高频细节最为丰富,其次是Freedman算法,Glasner算法最差。由图5的(c)和(f)可以看出,本文算法可以很好地重构图像的细节部分,尤其是对具有大面积纹理特征(如毛发)的图像也能够进行有效的恢复。
3.2 主观对比分析
针对不同的算法,选取各自算法最合适的参数以达到最好的效果。同一算法对不同图像选取相同的参数。主观效果如图6~图8所示,选择超分辨率图像的局部(如图中方框标记的部分)进行局部对比。对图6的处理中,Freedman算法和Glasner算法在数字的边缘处有很宽的过渡、锐度不够,Freedman算法在数字的边缘处产生了轻微振铃效应,Glasner算法在数字边缘比较模糊,本文算法边缘保持的很好,没有伪影等不良现象产生,边缘锐度较好。对图7的处理中,Glasner算法在帽子纹理边缘没有很好的清晰度和锐度,Freedman算法和本文算法的清晰度和锐度都很好,Freedman算法在脸部的边缘有类似于残影的不良现象产生,在相同的地方,Glasner算法比Freedman算法有更为严重的类似于残影的不良现象,本文算法不仅没有不良现象产生,而且具有非常好的清晰度和锐度。图8中,Glasner、Freedman算法和本文算法得到了纹理较为丰富毛发,但对马腿部分,本文算法比Glasner和Freedman算法有更好的对比度和细节保持效果。因此,从主观效果来看,本文算法效果整体优于对比算法。

图5 高频细节对比图

图6 3种算法超分辨率对比图(1)

图7 3种算法超分辨率对比图(2)
Fig.7 Comparison of three super-resolution algorithms(Ⅱ)

图8 3种超分辨率算法整体对比图
Fig.8 Comparison of three super-resolution algorithms
3.3 客观指标对比分析
用图像峰值信噪比(PSNR)和图像结构的相似性(SSIM)评价不同算法的性能。表1是测试图像在2倍超分辨率放大情况下的客观评价结果。可以看出,本文方法在所有情况下都比其他2种方法获得的结果要好。
为进一步评价不同算法超分辨性能,图6~图8比较了分别使用3种不同算法重建的结果。可以看出,Glasner算法不能有效恢复图像的高频信息,生成的图像有些模糊。与Glasner算法结果相比较,经典的Freedman算法通过学习HR与LR图像间的对应关系,在一定程度上能有效恢复出LR图像中丢失的高频细节,得到的结果比较清晰。从视觉质量上看,Freedman算法能够得到比Glasner算法更多的高频细节,但由于重建过程直接使用1次放大到需要的倍数,得到的图像在纹理细节区域仍出现明显的失真。与上述2种方法得到的结果相比,基于引导滤波和多尺度局部自相似性单幅图像超分辨率算法在保持图像边缘和恢复纹理细节方面都有不同程度的改善,得到的结果不仅边缘更清晰更真实,而且纹理更加丰富。这是由于图像的局部自相似特性在小的尺度因子范围下可以保持良好的特性,在邻域选择过程中,结合局部自相似特性,使得参与重建的图像块均与目标图像块具有相似的结构,因而能获得较好的重建质量。
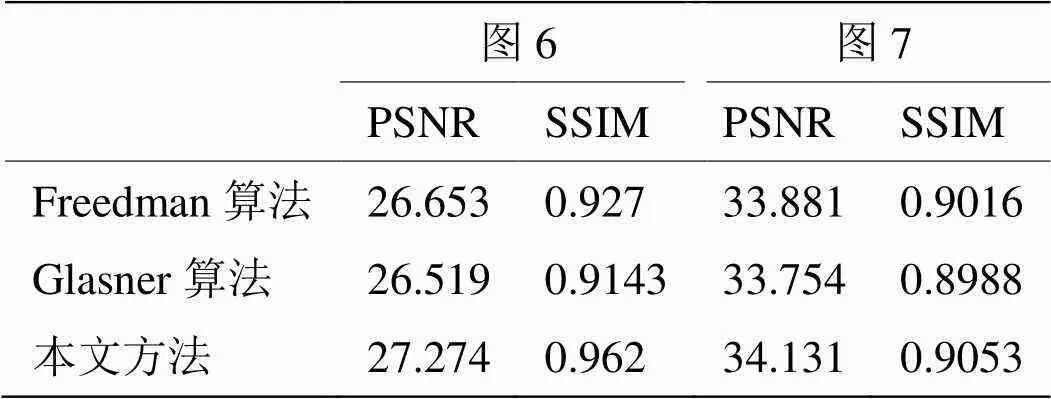
表1 3种超分辨率算法PSNR和SSIM的比较
4 结论
提出了基于多尺度局部自相似性和非局部均值单幅图像超分辨率算法。首先,引进了类高斯分布的“类高斯核”,在此基础上构建均值引导滤波器,该滤波器是一种线性边缘保持滤波器,可以得到图像的高频细节。其次,根据图像的自相似性,对初始高分辨率图像和原始低分辨率图像进行分块,得到待匹配窗和搜索窗,根据NLM,待匹配窗图像块的值利用搜索窗中相似块的加权平均计算得到。再次,利用图像自相似性,待匹配窗在搜索窗的邻域内进行匹配搜索,找到与待匹配窗最相似的匹配块,计算出最佳匹配块的高频细节图像块,与相似块的加权平均值相加,重构出高分辨率待匹配窗。最后,合并所有的超分辨率重构的待匹配窗,相邻图像块重叠区域的像素值使用平均融合得到,得到最终的超分辨率图像。实验结果表明,本文算法不仅能很好地重构图像的高频细节,还能很好地恢复图像的纹理特征,得到的结果不仅边缘更清晰更真实,而且纹理更加丰富。在下一步的研究中,将重点研究基于学习的多尺度自相似性单幅图像超分辨率算法。
[1] Nasrollahi K, Moeslund T B. Super-resolution: a comprehensive survey[J]., 2014, 25(6): 1423-1468. doi:10.1007/ s00138-014-0623-4.
[2] Van Ouwerkerk J D. Image super resolution survey[J]., 2006, 24(10):1039-1052.doi:10.1016/j.imavis.2006.02.026.
[3] Protter M, Elad M, Takeda H, et al. Generalizing the nonlocal-means to super-resolution reconstruction[J]., 2009, 18(1): 36-51.doi:10.1109/TIP.2008.2008067.
[4] Mairal J, Bach F, Ponce J, et al. Non-local sparse models for image restoration[C]//12th,Kyoto, Japan, 2009: 2272-2279.
[5] Suetake N, Sakano M, Uchino E. Image super-resolution based on localself similarity[J]., 2013, 15(1): 26 -30 .doi:10.1007/ s10043-008-0005-0.
[6] Glasner D, Bagon S, Irani M. Super-resolution from a single image[C] //12th, Kyoto, Japan, 2009: 349-356 . doi:10.1109/ICCV.2009.5459271.
[7] Freedman G, Fattal R. Image and video up scaling from localself -examples[J]., 2011, 30(2):1-11. doi: 10.1145/1944846.1944852.
[8] Kawano H, Suetake N, Cha B, et al. Sharpness preservingimage enlargement by using self-decomposed codebook and Mahalanob is distance[J]., 2014, 27(6): 684-693. doi:10.1016/j.imavis.2008.07.013
[9] ZHANG Y Q, LIU J Y, YANG W H, et al. Image super-resolution based on structure-modulated sparse representation[J]., 2015, 24(9): 2797-2810. doi:10.1017/ s11444-014 -5768-4.
[10] ZHANG Y Q, XIAO J S, LI S H, et al. Learning block-structured incoherent dictionaries for sparse representation[J]., 2015, 58(10): 1-15. doi:10.1007/s 11432-014-5258-6.
[11] YANG C Y, HUANG J B, YANG M H. Exploiting self-similarities for single frame super-resolution[C]//10th(ACCV), Queen-stown, New Zealand: Springer, 2016: 497-510.
[12] Glasner D, Bagon S, Irani M. Super-resolution from a single image[C]//12th(ICCV). Kyoto, Japan, 2009: 349-356. doi:10.1109/ ICCV.2009. 5459271.
[13] Schulter S, Leistner C, Bischof H. Fast and accurate image up scaling with super-resolution forests[C]//2015, Boston, MA, 2015: 3791-3799.
[14] Sajjad M, Ejaz N, Baik S W. Multi-kernel based adaptiveinterpolation for image super-resolution[J]., 2015, 72(3): 2063-2085. doi:10.1109/CVPR.2015.7299003.
[15] Catalin Ionescu, Orestis Vantzos, Cristian Sminchisescu. Matrix back propagation for deep networks with structured layers[C]//, 2015: doi:10.1101/ ICCV.2015.65789987.
[16] Getreuer P. Contour stencils: total variation along curvesfor adaptive image interpolation[J]., 2011, 4(3): 954-979. doi:10.1137/100802785.
[17] XIAO Jinsheng, DU Kanghua, TU Chaoping, et al. Bokeh display based on depth information extraction of multi-focus images[J]., 2015,41(2): 304-311.
[18] XIAO J S, LI W H, LIU G X, et al. Hierarchical tone mapping based on image colour appearance model[J]., 2015, 8(4): 358-364.
Single Image Super Resolution Method Based on Multi-scale Self-similarity and Non Local Means
LIU Zhe,HUANG Shiqi,JIANG Jie
(,,’710123,)
In this paper, we propose a new single image super resolution algorithm based on multi-scale local self-similarity and non local means. This algorithm does not rely on an external example database nor use the whole input image as a source for example patches. Instead, we extract similar patches from extremely localized region in the input image, similar patches are weighted summed to estimate the image to be restored using a non-local mean algorithm, and then the high frequency detail image of the most similar patch is added to the restored image to obtain a high-resolution image. Experimental results show that the proposed algorithm can not only reconstruct the high frequency details of the image, but also restore the texture features of the image.
super resolution,multi-scale,self-similarity,non-local mean
O121.8,G558
A
1001-8891(2017)04-0345-08
2016-11-02;
2016-12-28.
刘哲(1972-),男,博士,教授级高工,研究方向为机器视觉、人工智能及模式识别。
国家自然科学基金(61473237)资助。
