基于组合赋权法的多元SPA-ITFN模型在再生水评估中的应用研究

张铖铖，杨 侃，刘建林，钟金华，邱光树，谷桂华，文娅丹，姜 敏，范 莹

(1.河海大学水文水资源学院，南京 210098；2.云南省水利水电学校，昆明 650224；3.云南省水文水资源局玉溪分局，云南 玉溪 653100；4.云南省水文水资源局丽江分局，云南 丽江 674199)

0 引 言

再生水综合发展能力是多种确定性因素与不确定性因素相互作用的产物，其评估工作对于缺水地区的再生水开发利用具有指导性意义。现阶段的再生水评估工作取得了一定的进展，但仍存在一定的缺陷。传统的再生水评价指标体系[1]多集中于效益、风险和水质等单方面评估，这些指标体系只能反映再生水的单方面特性，具有一定的局限性，难以对再生水进行综合评估。结合再生水评估工作的实际情况，需建立再生水综合评价指标体系，从再生水需求程度、利用条件及效益风险等角度全面评价再生水综合发展能力。常用的评估方法，例如模糊综合评价法、人工神经网络法、突变级数法等，其在不同评估工作中取得了不同的优越性，但这些方法均是根据确定的指标等级标准进行求解，忽略了评价指标在各个评价等级具有同异反联系的客观事实[2]。集对分析(Set Pair Analysis，SPA)理论通过建立联系度概念，能够准确剖析系统的同异反特性；利用多元联系度和区间三角模糊数(Interval Triangular Fuzzy Number，ITFN)克服标准SPA理论中同异反评语的细化问题和差异度系数的量化问题，葛康等[3]将该理论应用于土壤污染评价，彭涛等[4]将该理论应用于湿地生态系统的健康评价，均取得了合理的结果。指标权重计算方法各有优劣，如熵值法能有效减少主观性，但单考虑评价标准间的差异性会得出荒谬的结论[2]；超标倍数法作为一种主因素突出赋权法，能有效避免熵值法的缺陷，但不同的权重定义使评价结果相差很大[5]。王颖等[2]利用超标倍数法和熵值法进行组合赋权，避免了使用单一赋权方法容易出现的问题，在水质综合评价工作中取得了良好的结果。本文综合考虑再生水评估工作中主客观因素及实际情况，首先建立“压力-条件-影响”再生水综合评价指标体系，利用基于组合赋权法的多元SPA-ITFN模型对再生水进行评估，并通过实例对该模型的合理性进行验证。

1 再生水综合评价指标体系

再生水综合评价的前提，就是要建立合适的评价指标体系，其需遵循一致性、系统性、独立性、客观性、简洁性和数据可获得性等原则。为描述再生水综合发展能力，本文根据前人研究成果，结合实际情况并考虑诸多因素，建立了如表1所示的“压力-条件-影响”再生水综合评价指标体系。

该指标体系中，压力指标(B1)描述再生水利用的需求状况，包括现阶段的水资源压力(D1～D3)与环境压力(D4～D5)；条件指标(B2)描述再生水开发利用的经济条件(D6～D7)、技术条件(D8～D10)和社会条件(D11～D12)；影响指标(B3)则描述再生水利用的经济影响(D13)和潜在风险(D14～D16)。

部分指标的含义如下：地下水替代量D3是指为解决现阶段供水不足的难题而增加的地下水供水量；一级A/B处理水平D9/D10是指污水处理厂排水水质所能达到的处理标准；系统综合净效益D13为再生水开发利用效益与费用的差值；污水回用不确定性D14是指再生水项目后期能力发挥的衰退程度；水质风险D15是指处理后的再生水水质的潜在危害程度；施工影响D16是指项目实施对周边环境的负面效应。在各项指标中，D1～D13为越大越优型指标，D14～D16为越小越优型指标。

表1 “压力-条件-影响”再生水综合评价指标体系Tab.1 “Pressure-Condition-Influence” comprehensive evaluation index system of reclaimed water

2 基于组合赋权法的多元SPA-ITFN再生水评估模型

2.1 标准集对分析(SPA)与多元联系度

集对分析的基本原理是将评价指标实际值{Xgp|g=1,2,…,h;p=1,2,…,m}与评价标准{Skp|k=1,2,…,n;p=1,2,…,m}两个集合视为一组集对，对其进行同异反的系统剖析，并计算联系度：

μ=a+bi+cj

(1)

式中：a为同一度，描述该组集对中共有特性所占的比例；c为对立度，描述对立特性所占的比例；b为差异度，描述除共有、对立以外的特性所占的比例。a,b,c均为非负，且a+b+c=1。i,j分别为差异度系数和对立系数，取值范围为i∈[-1,1]，j=-1，均可仅视为一种标记。

标准SPA理论仅能对样本所处的状态“一分为三”，由此建立的三元联系度通常不能满足实际要求，需对联系度表达式进行不同层次的拓展，即实现同异反评语的细化[3]，建立多元(k元)联系度表达式为：

μ=a+b1i1+b2i2+…+bk-2ik-2+cj

(2)

式中：a+b1+b2+…+bk-2+c=1，b1,b2,…,bk-2为差异度；i1,i2,…,ik-2∈[-1,1]均为差异度系数。

本文在再生水评估问题中引入五元联系度，能充分满足再生水评估的实际要求，同时避免使问题复杂化，其联系度公式为：

μ=a+b1i1+b2i2+b3i3+cj

(3)

2.2 区间三角模糊数(ITFN)

联系度表达式中差异度系数i的量化一直是集对分析评价模型中亟待解决的问题，两相邻评价等级之间的i呈现着十分显著的模糊性，同一等级的i也有所差别。三角模糊数能较好地处理不确定性问题中信息的模糊性和随机性，但单一三角模糊数不足以清楚表示实际问题[3]，故本文引入ITFN来解决差异度系数i的量化问题，彻底解决再生水评估问题中的模糊性和随机性。

定义1：设在实数域R上的一个模糊数A，定义一个隶属函数：μA(x):R→[0,1](x∈R)，假如隶属函数μA(x)表示为：

(4)

那么称A为ITFN，即A=(a1,b1,c1,a2,b2,c2)，ITFN分布图如图1所示。

图1 区间三角模糊数Fig.1 Interval triangular fuzzy numbers

2.3 组合赋权法

引入距离函数将熵值法和超标倍数法进行组合赋权，对二者进行线性加权，得到综合权重。

2.3.1 熵值法

将第g个样本的第p个实测指标值{Xgp|g=1,2,…,h;p=1,2,…,m}按式：

(5)

求解其归一化矩阵：

(6)

利用式：

(7)

计算X′gp在不同样本的同指标值之和中所占的比重。计算第p个指标的熵：

(8)

最终得到由熵值法计算出的第p个指标的权重：

(9)

2.3.2 超标倍数法

由超标倍数法计算第p个指标的权重：

(10)

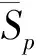
2.3.3 组合赋权得综合权重

利用线性加权得综合权重：

wp=αw′p+βw″p

(11)

式中：α,β分别为熵值法与超标倍数法权重的分配系数，α+β=1。

为将α,β量化，引入距离函数d(w′,w″)建立二者之间的关系式：

(12)

[d(w′,w″)]2=(α-β)2

(13)

式中：距离函数d(w′,w″)为熵值法与超标倍数法所得权重的差异程度，令其与α,β的差异程度相等，可保证差异程度的一致性[6]。α,β值确定后，由公式(11)求得各指标综合权重wp。

2.4 基于组合赋权法的多元SPA-ITFN再生水评估

按照标准SPA理论，将再生水综合评价指标体系中各指标的实际值与评价标准两集合视为一组集对，结合多元联系度理论构建五元联系度表达式，以实现同异反评语的细化；结合ITFN对联系度表达式中的差异度系数进行量化，对联系度进行定量表示；利用熵值法与超标倍数法对各指标进行综合赋权，进而实现再生水的综合评价，具体步骤如下：

步骤1：再生水评价中各指标实际值与评价标准的五元联系度表达式写成如下形式：

(15)

式中：μgp指第g个评价样本中第p项指标的联系度；x指某项指标实测值；s1～s4分别表示一到五级评价等级的界限值。公式(14)对应于越小越优型指标，公式(15)对应于越大越优型指标。

步骤2：引入区间三角模糊数(ITFN)理论量化i，即通过分析取值法将评价等级二到四级中心点处的i分别确定为i1=0.5，i2=0，i3=-0.5，两等级界限之间的i如图2所示。

图2 差异度系数的量化Fig.2 Quantification of the difference coefficient

指标的差异度系数按下式计算：

(16)

(19)

(20)

(21)

式中：公式(16)～(18)表示越小越优型指标的差异度系数计算表达式，公式(19)～(21)则表示越大越优型指标的差异度系数计算表达式。将公式(16)～(18)与公式(14)联立，得越小越优型指标的联系度表达式：

(22)

同理，将公式(19)～(21)与公式(15)联立，得越大越优型指标的联系度表达式：

(23)

步骤3：利用式(11)计算各指标综合权重，再结合SPA单指标联系度，可得总体联系度μg，以实现再生水的综合评价。

(24)

式中：wp为各指标综合权重。再生水综合发展能力等级划分为：当μg∈[0.6,1]时为一级；μg∈[0.2,0.6)时为二级；μg∈[-0.2,0.2)时为三级；μg∈[-0.2,-0.2)时为四级；μg∈[-1,-0.6)时为五级。

图3为基于组合赋权法的多元SPA-ITFN再生水评估流程图。

图3 基于组合赋权法的多元SPA-ITFN再生水评估流程图Fig.3 Calculation flow chart of diversified SPA-ITFN reclaimed water assessment based on combination Weighting Method

3 实例应用

3.1 数据收集

利用本文所构建的再生水评估模型评价某市Q、Z、F、M共4个县区的再生水发展能力，以说明该模型的合理性。各县区基本情况如下: Q县为该市政治经济中心，GDP及工业总产值较高，废污水排放量大，6个污水处理厂均为一级A处理水平，污水处理技术水平高，其再生水开发利用的需求大、条件好，其再生水发展能力较高； M县的经济发展水平低，废污水排放量也少，仅有一个一级A处理水平的污水处理厂，用户接受度低，利用风险较高，再生水开发利用的需求小、条件差，其再生水发展能力较低；Z、F为该市经济发展水平较为一般的城市，相应的再生水处理水平、用户接受度较为一般，其再生水发展能力一般。根据现有资料，4个县区的再生水综合发展能力由高到低为Q>F>Z>M。

数据的收集工作主要包括两部分：再生水综合评价指标体系中各项指标实际值和各项评价指标的分级标准。表2为4个县区再生水综合评价各项指标实际值，其中大部分数据是通过查阅该市2015年统计年鉴与水资源公报获得；其他指标如定量指标D9、D10根据污水量与污水处理量计算求得；定量指标D13参考文献[7]中的效益-费用模型计算求得；定性指标D11、D14、D15、D16根据经验丰富的专家打分并结合实际情况获得；定性指标D12以调查问卷与数据统计的形式获得。

通过查阅相关资料、咨询专家，最终确定4个县区再生水综合发展能力评价等级标准如表3所示。在该标准中，各项指标的等级越低，表明该县再生水的综合发展能力越好。

表2 某市四县再生水相关指标值统计表Tab.2 Index statistics related to reclaimed water

表3 评价指标分级标准Tab.3 Grading standards of evaluation index

3.2 数据处理

数据处理包括三部分：单项指标联系度的计算、各指标综合权重的确定、各县区总体联系度的求解，其具体步骤如下：

步骤1：用越大越优型单项指标联系度公式计算4个县区D1～D13；用越小越优型单项指标联系度公式计算4个县区D14～D16。

步骤2：分别计算各指标熵值法权重和超标倍数法权重；根据分配系数 ，计算各指标的综合权重。

步骤3：计算各县区的压力联系度、条件联系度和影响联系度，最终得总体联系度。

计算结果见表4。

表4 4个县区再生水综合评价结果Tab.4 Comprehensive evaluation results of reclaimed water in four counties

3.3 结果分析

分析表4可知：对于Q县，D1～D10联系度大，说明该县再生水开发利用的需求压力大、经济和污水处理技术条件好，且再生水开发利用条件>压力>影响，再生水综合发展能力强，属一级水平，但D14和D16联系度一般，说明该县再生水利用存在一定的风险；对于F县，其再生水需求压力较大，但经济水平却较为一般，且再生水开发利用压力>条件>影响，其再生水综合发展能力较强，属二级水平，其D6、D7和D8联系度偏低，说明该县应着重提高其经济水平与污水处理规模；对于Z县，其水资源压力小，水环境压力大，污水处理条件较差，但经济水平一般，且再生水开发利用条件>压力>影响，其再生水综合发展能力一般，属三级水平，其D8和D9联系度低，说明该县当务之急应着重提高其污水处理规模及技术水平；M县的16项指标的联系度多数均为负值，经济发展水平低，废污水排放量也少，反映该县再生水开发利用的需求程度低、经济条件差，且再生水开发利用影响>条件>压力，因而再生水综合发展能力较差，属四级水平，现阶段可不着重要求发展再生水。

图4是4个县区再生水综合评价结果图。4个县区再生水综合发展能力评估值由大到小分别为Q县、F县、Z县、M县。Q县的再生水综合发展能力最高，F县和Z县的再生水综合发展能力一般并相近，M县的再生水综合发展能力最差，这与各县区的实际情况一致，说明了本文构建的再生水综合评估模型具有合理性。

图4 再生水综合评价结果图Fig.4 Comprehensive evaluation results graph of reclaimed water

4 结 论

本文引入“压力-条件-影响”再生水综合评价指标体系，建立了基于组合赋权法的多元SPA-ITFN模型，并对某市4个县区的再生水综合能力进行评估，四个县区再生水综合发展能力大小为Q县>F县>Z县>M县，计算结果与实际相符。说明本文构建的指标体系完整，模型正确，分析方法可行，在再生水综合发展能力评价方面具有一定的实用性。

□

[1] 孙 静. 北京市非传统水资源利用潜力及效益综合评价研究[D].北京：中国水利水电科学研究院,2007.

[2] 王 颖, 邵 磊, 杨方廷,等. 改进的集对分析水质综合评价方法[J]. 水力发电学报, 2012,31(3):99-106.

[3] 葛 康, 汪明武, 陈光怡. 基于集对分析与三角模糊数耦合的土壤重金属污染评价模型[J]. 土壤, 2011,43(2):216-220.

[4] 彭 涛, 陈晓宏, 王高旭,等. 基于集对分析与三角模糊数的滨海湿地生态系统健康评价[J]. 生态环境学报, 2014,(6):917-922.

[5] 阚宝珠, 付 强, 宋族鑫. 基于超标倍数赋权法的模糊物元在湿地水质评价中的应用[J]. 安全与环境学报, 2009,9(1):97-99.

[6] 李 浩, 杨 侃, 陈 静,等. 灰色三角白化权集对分析模型在河流健康评价中的应用[J]. 水电能源科学, 2015,(8):33-36.

[7] 张光连. 北京市再生水综合利用规划研究[D]. 北京:中国农业大学, 2005.

[8] 舒持恺, 杨 侃, 王启明, 等. 河流健康评价中赋权方法的研究[J]. 水电能源科学,2017,(2):61-65.

[9] 孟宪萌, 胡和平. 基于熵权的集对分析模型在水质综合评价中的应用[J]. 水利学报, 2009,40(3).