离心泵水力设计及流固耦合数值模拟
2017-03-22李林军王建国
李林军,王建国
(江苏振华泵业股份有限公司,江苏 泰州 225500)
0 引 言
计算流体力学(CFD)作为流体力学的学科分支,在计算机技术和多领域交叉学科的推动下,取得了相当迅速的发展并趋于成熟。当前,计算流体力学从定性分析发展到定量计算,成为CAD系统中一个重要组成部分。通过数值模拟计算,可以充分认识泵内流动规律,方便地评价、选择多种设计方案,进行优化设计,大幅减少实体试验工作量,因此,CFD计算结果越来越多地被水泵生产者所使用。
本文采用水力设计与CFD数值计算相结合的方式对离心泵优化设计,基础水力模型经过三维制图、网格划分后进行CFD计算,获得的水力性能参数反馈给水力设计,进行水力修正,重复这一过程,直至获得较好的泵内流态和外特性。随着时代的进步,在水泵业节能高效的要求下,现有的水力模型大部分不能达到节能标准,故相关企业需要新型的高效水力模型来达到国内的节能标准。水力设计中,出现了很多值得借鉴的宝贵经验[1],同时亦存在一些误区,列举部分如下:①单一的考虑叶片的水力性能,却忽略了叶轮与蜗壳(导叶)的匹配特性;②计算出口角时,普遍采用滑移计算,实际计算结果偏大,造成叶片脱流,效率较低,甚至出现性能曲线驼峰。③受传统叶片加工方法的限制,叶片包角取值偏小。
在CFD计算的基础上,流固耦合计算把水动力学与固体力学结合起来,使其真正成为一个跨学科领域。近年来,国内外不少学者尝试采用流固耦合的方法对泵转子系统进行力学性能分析,取得了许多有价值的成果[2-5],但也存在以下问题:①往往局限于叶轮等单个零件的力学分析,未能考虑整个转子系统;②施加到固体结构的流场载荷仅限于叶轮和蜗壳内流场,未能考虑叶轮前后腔的流场载荷。
根据上述情况,本文运用ANSYS workbench软件,对离心泵包括叶轮、螺母和轴等转子系统进行单向流固耦合分析[6]。在流固耦合计算中,施加到固体结构上的流场载荷不仅有叶轮和蜗壳内流场,同时还考虑叶轮前后腔的流场载荷。此外,为了解泵转子系统的固有频率和振型等问题,本文还对转子系统进行模态分析,得到其固有频率和振型。
1 离心泵性能参数及水力设计
1.1 计算模型
离心泵参数如下:流量Q=160 m3/h,扬程H=32 m,转速n=2 960 rpm,汽蚀余量NPSHr=5.5 m。
1.2 水力设计
1.2.1 比转速
(1)
美标比转速:
Ns=2 393
(2)
通用比转速:
(3)
气蚀比转速:
(4)
1.2.2 借助经验公式近似确定泵的总效率
(5)
1.2.3 叶轮主尺寸计算
1.2.3.1 Stepanoff、Paul Cooper设计理论计算
流量转速比Q/N=0.24 (Anderson研究成果)。
压头系数:
(6)
出口半径:
(7)
出口流量分数:

(8)
出口宽度:
(9)
进口半径:

Dj=106.8~122.2 mm
(10)
1.2.3.2 Lobanoff、Ross设计理论计算
按Lobanoff设计法计算叶轮外径,5叶片与6叶片模型共用取值曲线(图1~图3)。

图1 ku-Ns取值曲线Fig.1 ku-Ns take parameter on trendline

图2 km2-Ns取值曲线图Fig.2 km2-Ns take parameter on trendline

图3 (Dj/D2)-Ns取值曲线图Fig.3 (Dj/D2)-Ns take parameter on trendline
查图1:
ku=0.93+0.000 083Ns=1.129
(11)
叶轮外径:
(12)
查图2:
km2=0.159
(14)
出口宽度:
(15)
查图3:
(16)
综合两种设计方法,经前言所述设计流程,迭代优化36次,得到最佳叶轮尺寸D2=180 mm,b2=35 mm,Dj=110 mm。
1.2.3.3 叶片其他尺寸计算
根据设计要求,设计点到关死点斜率为25%~30%,流量扬程曲线较平坦,根据Lobanoff设计要求:
取叶片数为Z=5,β2=23°,包角φ=135°。
何希杰经验公式:
β2Z0.723≤90
(17)
式(17)保证流量扬程曲线不出现驼峰。
泵体沿用原泵体,经过叶轮蜗壳尺寸匹配,面积比Y=1.1,根据Anderson面积比原理[7],面积比取值在最佳选择范围内。
其余叶片水力模型设计过程在此不再赘述。
2 全流场CFD分析及试验结果
2.1 过流部件及固体部件三维造型
采用三维软件Creo对进水管、叶轮、泵体、前后腔、出水管等流体部件,叶轮、螺母及轴等固体部件进行三维造型,各部件造型如图4、图5所示。

图4 流体域各部件Fig.4 Components of fluid domain

图5 固体域各部件Fig.5 Components of solid domain
2.2 网格划分及控制方程
2.2.1 网格无关性
采用CFX前处理软件ICEM对过流部件进行网格划分,网格质量(均大于0.25)并对网格数进行无关性检查,表1中,中密两种网格数,对扬程的计算结果影响很小,认为网格无关性。流体域及固体域网格见图6,图7。
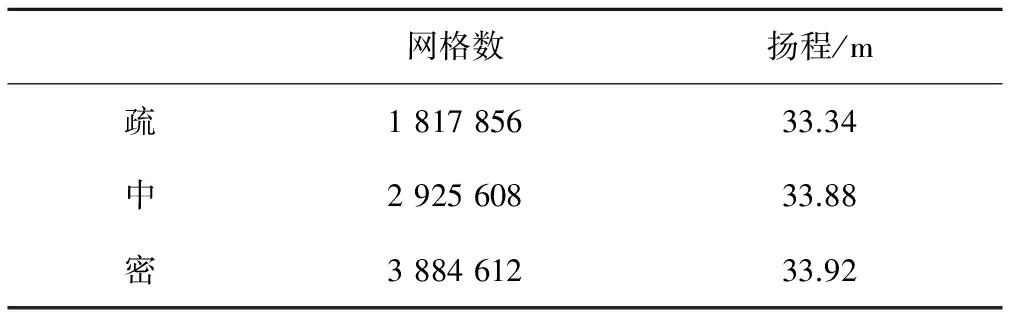
表1 网格无关性Tab.1The grid independence

图6 流体域网格Fig.6 Grid of fluid domain

图7 固体域网格Fig.4 Grid of solid domain
2.2.2 控制方程
质量守恒:
(18)
动量守恒:
(19)
湍流时均N-S方程:
(20)
湍流模型选用SSTk-w模型:在自由流区域和边界层外层使用k-ε模型,在近壁面区域使用k-w模型,在混合区域通过加权函数来混合使用这两种模型。
2.2.3 边界条件及计算设置
(1)进口边界条件采用速度进口,设置为inlet,根据不同流量计算不同进口速度值。
(2)出口边界条件采用压力出口且假定压力为均匀分布,设置为outlet。
(3)叶片、前后腔边界均设置为固壁条件,采用无滑移的边界,壁面粗糙度为12.5。
(4)叶轮设置为旋转体,动静交接面为Frozen Rotor。
(5)设置计算残差和监视水泵扬程的稳定程度判断计算收敛情况,残差值设置为10-5。
2.3 外特性计算结果
外特性计算结果见表2。
2.4 泵内流场分布(160 m3/h工况)
从图8中可以看出,叶轮内流线在设计工况下,完全贴合叶片壁面,从叶尖至叶末无脱流、回流、漩涡等现象,速度变化线性稳定。

图8 叶轮内流线Fig.8 streamline in the impeller
3 流固耦合计算
3.1 转子系统结构及约束条件
离心泵转子系统简化为叶轮、螺母和轴3部分,组装图如图5所示,计算泵转子的材料为结构钢,其物性参数见表3。将离心泵转子实体导入ANSYS workbench中进行实体和边界定义,对转子系统进行网格划分,网格如图7所示,网格数为235 452。

表3 转子材料物性参数Tab.3 Material physical parameters of the rotor
载荷条件如下:
(1)转子旋转产生的离心力,此力通过对叶轮施加旋转角速度来实现,ω=309.97 rad/s;
(2)自身重力,通过设置标准重力实现,方向为-Z轴;
(3)流体对转子的内外压力,流场压力载荷从流场计算获得,并通过流固耦合界面传递到固体结构。
对于转子系统的约束条件,通过两个滚动轴承进行刚性支撑,对转子进行轴向和径向限制。在计算中采用了圆柱(Cylindrical)方法对轴与轴承接触部位进行轴向和径向约束,对切向采用自由约束,转子结构的受力和约束如图9所示。

图9 转子系统的受力和约束Fig.9 The stress of the rotor system and constraints
3.2 转子系统计算结果与分析
3.2.1 应力分布
图10为转子系统在设计工况下的等效应力分布,从图10中可以看出转子系统的最大应力位于叶轮轮毂圆柱面上,最大等效应力为14.48 MPa。

图10 设计工况下转子的等效应力分布Fig.10 The equivalent stress distribution of the rotor at design point
3.2.2 变形分布
图11为转子系统在设计工况下的变形分布。从图11中可以看出,转子系统的最大变形位置在叶轮的外缘处,最大总变形量约为0.086 mm,叶轮变形主要表现为沿径向的拉伸变现,变形量随半径的增大而增大,轴的变形相对较小,因此在离心泵转子设计时需考虑叶轮出口的变形量。

图11 设计工况下转子的变形分布Fig.11 The deformation distribution of the rotor at design point
3.2.3 转子的模态分析
表4为计算得到离心泵前6阶固有频率,通过分析各阶振型图12发现,1阶振型变形量呈轴中心对称分布且叶轮的变形随半径增大而增大;2阶和3阶振型均为弯曲振动,最大变形量出现在叶轮轮毂处和叶轮外缘;4阶和5阶振型为弯曲和扭转的复合振动;6阶振型的变形较小,但轴产生了严重的扭转变形且变形量呈轴中心对称分布。

表4 离心泵前6阶固有频率Tab.4 6 extended natural frequency of centrifugal pump

图12 各阶振型变化规律Fig.12 Change rule of each order modal
从表4中可以得到,该系统的一阶临界转速为1 046 r/min,二阶临界转速为15 548 r/min,由于一阶振型为轴中心对称分布且叶轮的变形随半径增大而增大,可认为为安全转速,二阶临界转速远大于实际运转速度2 960 r/min,故认为该转子系统运转安全。
4 CFD计算结果及试验结果对比
按GB/ T 3216-2005《回转动力泵水力性能验收试验1 级和2 级》标准在B 级精度试验台上对离心泵的样机进行性能试验,测得试验数据如表5所示,试验结果与计算结果相差也不大,其差异是离心泵在铸造、机加工及表面粗糙度等因素引起的,因此,建立的数值模型和计算方法是可信的,可以用数值模拟对离心泵进行汽蚀性能预测和分析。
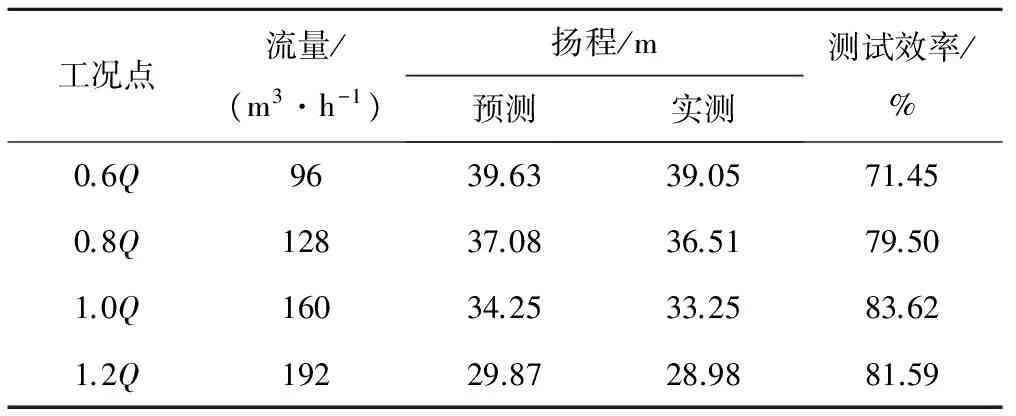
表5 计算与试验结果对比Tab.5 Calculation compared with experimental results
原模型性能参数:流量Q=160 m3/h;扬程H=34.82 m;转速n=2 960 rpm;效率η=77.53%。
从表5中可以看出,通过分析CFD计算结果,对水力设计进行优化,多步迭代,得到了令人满意的结果,该水力模型效率超过现模型6.09%,超过节能标准2.12%。
5 结 语
经过对离心泵的水力优化及全流场流固耦合分析,验证了水力设计和CFD数值分析相结合的科学性和可靠性。
(1)在水力设计过程中,采用新的水力设计方法与CFD数值计算结合,多次迭代计算至获得满意的泵内流态及其外特性。经过CFD预测结果与试验结果的对比分析,认为CFD计算结果准确可靠,优化后的水力模型效率达到83.6%,超过现模型6.1%,超过节能标准2.1%。
(2)对叶轮转子系统力学的分析中,对轴承与轴承接触处采用轴向与径向约束,进行模态分析,得到其6阶模态的固有频率和振型。计算结果表明:二阶临界转速为15 548 r/min,二阶临界转速远大于实际运转速度2 960 r/min,故认为该转子系统运转安全。
□
[1] 李 彤,周建佳,袁寿其. 基于流场计算的螺旋离心泵叶轮静力学分析[J].流体机械,2013,41(12):22-26.
[2] 黄浩钦,刘厚林,王 勇,等. 基于流固耦合的船用离心泵转子应力应变及模态研究[J]. 农业工程学报,2014,30(15):98-105.
[3] 陈 宁,成晓伟,陈乃娟. 多级离心泵转子部件有限元分析[J]. 科学计算与工程,2010,(6):18-21.
[4] 刘 君,袁建平. 带预应力的高速离心泵转子模态分析[J]. 中国农村水利水电,2014,(2):117-121.
[5] 王海玉,张德胜,施卫东,等. 基于流固耦合的离心泵蜗壳结构分析与优化[J]. 排灌机械工程学报,2014,32,(3):185-190.
[6] Saeed R A,Galybin A N. Simplified model of the turbine runner blade[J]. Engineering Failure Analysis,2009,16(7):2 473-2 484.
[7] 关醒凡. 现代泵技术手册[M]. 北京:宇航出版社,2011:359-362.
