节制闸调控下明渠输水系统水力特性研究
2017-03-22李毅佳
李毅佳,马 斌,周 芳
(1. 天津理工大学 管理学院,天津 300384; 2. 天津大学水利工程仿真与安全国家重点实验室,天津 300072)
0 引 言
我国水资源丰富,但在时间和空间上存在分布不均匀的特点,随着经济社会的发展,我国水资源问题日益突出。为实现水资源在空间上的合理配置[1],我国先后在长江、黄河、淮河和海河等流域建成和在建了很多调水工程,其实质是通过水力控制改变水流的自然流动方向。其中长距离明渠输水工程作为一种重要输水方式,在跨流域调水工程中占有重要地位[2],很多输水工程均采用该方式,例如南水北调中线工程。长距离明渠输水工程通常会在沿线设置众多的节制闸,通过对各节制闸的调控来实现对输水工程运行过程中渠道水量输运的控制与调度。因此,对长距离输水工程中明渠输水系统的水力控制问题开展研究,特别是对其控制运行方式、闸门启闭方式和调控方法的优化,将有助于实现输水工程的高效运行,提升输水工程的安全可靠性。
20世纪30年代,法国最早研制了水力自动闸门并提出了渠系控制方法。20世纪50年代以后,法国、美国、日本等发达国家大力发展了渠系自动化技术。我国这方面的研究虽然起步较晚,但得益于大量输水工程的规划、设计、建设和运行的实际需求,我国的水利工作者对长距离输水系统的实时控制相关问题开展了大量研究工作。王长德[3,4]针对渠道水力闸门控制运行的稳定问题和上游常水位自动控制渠道明渠非恒定流动态边界条件等问题开展了研究,完善了单渠池水力自动闸门的运行控制问题。王念慎[5]等将状态空间方程和现代控制理论引入到渠道水力控制研究中,提出了明渠瞬变流的等容量最优控制模型。王涛、杨开林[6]在线性化明渠瞬变流的圣维南方程的基础上,结合现代控制理论和数字仿真技术,实现了输水系统水力控制过程动态仿真的可视化。韩延成[7]对长距离调水工程中的渠道运行控制模型进行了研究,提出将传统渠道下游常水位输水PID控制和RBF人工神经网络结合的非线性输水控制方法。但总体来说,输水工程中的水力自动控制理论尚不完善,闸门的优化控制和启闭方式等诸多方面还存在很多问题亟待解决。
本文以南水北调中线总干渠的陶岔至黄金河段为工程背景,建立非恒定流模型,对几种节制闸调控工况下的输水系统水力特性进行研究,包括节制闸调节速度对水面线影响、节制闸突然关闭时引起的水力震荡及水流漫溢现象,以及节制闸间距对渠道响应时间、闸前水位壅高、事故排空时间、建闸投资比等的影响。
1 明渠输水系统非恒定流数学模型
1.1 基本方程
渠道水流特征可以采用圣维南方程表示:
(2)
式中:Q为流量;y为水深;x为沿水流运动方向的距离坐标;t为沿水流运动方向的时间坐标;A为过水断面面积;B为过水断面宽度;Sf为能坡;S0为底坡;g为重力加速度。
1.2 求解步骤
将渠道离散化,概化的渠道系统离散图[8]如图1所示,其中i表示渠段,j表示渠段内的计算断面,Qij为第i渠段第j计算断面的流量,Zij为第i渠段内第j计算断面的水位,i=1,2,…,m;j=l,2,…,n。当采用不同的运行控制方式时,对各断面的水位要求是不同的,当采用闸前常水位运行方式时,要求渠段末端(即闸前)计算断面的水位Zn不变,采用中点常水位运行方式时则要求渠段中点的水位Z中不变,而采用上游常水位运行方式时则要求上游水位Z1不变。
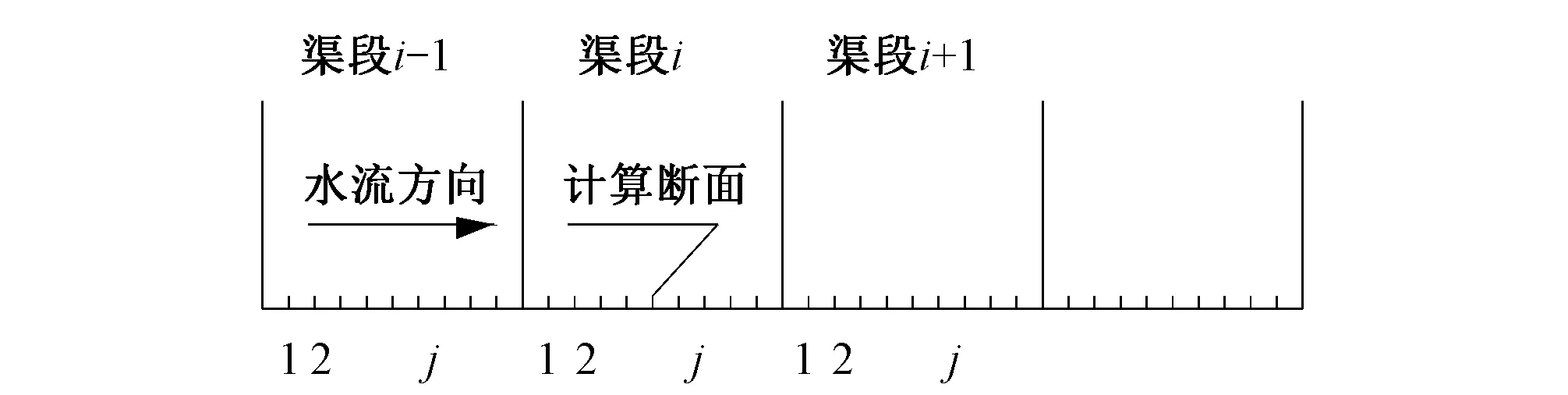
图1 渠道系统离散图Fig.1 Discrete graph of channel system
(1)恒定流计算。

② 水位。当不同调度方式时的水位计算方法略有差别。上游常水位调度模式与闸前常水位调度模式的计算方法类似。以闸前常水位调度方式为例,将第i渠段的下游节制闸的闸前水位设为已知恒定值Zn,采用龙格库塔法求解明渠渐变流常微分方程,即可自下游向上游逐步计算出各断面水位,至第i渠段的第1个计算断面终止。若采用中点常水位调度模式时,计算时将渠道中点水位Z中设为已知的恒定值,然后依次向上游和下游逐断面计算。
③闸门开度。若计算第i-1渠段设置的节制闸的闸门开度,可先通过上述的流量及水位计算过程分别求出其闸前水位、闸后水位、过闸流量,再利用闸孔出流公式采用迭代法计算得到。
(2)非恒定流计算。利用恒定流计算模型可以计算得到输水系统在初始稳定运行工况和调控后形成的新稳定运行工况下的各种参数,包括各渠段的水面线、各断面的水位、各分水口及节制闸的过流量、各节制闸的闸门开度等。而当各节制闸的启闭控制规律已知时,可通过非恒定流计算求出整个输水渠道系统的水力瞬变过程,本文中的非恒定流计算采用特征线法。
1.3 算 例
本文以南水北调中线一期工程总干渠的陶岔至黄金河段为算例,对节制闸调控时各种工况下的输水系统水力特性进行研究。该渠系全长160 km,将其闸首段作为典型渠段进行计算分析。渠段1长36 488 m,底宽20 m,底坡1/25 000,边坡系数是3,糙率是0.014,设计流量350 m3/s。假设渠段上游为一大型水库,保持水深8.5 m不变。渠段1下游闸前常水深是8.0 m,渠段示意图如图2所示。假定在渠道的运行过程中,渠段2末段水位保持不变,闸门同步启闭。

图2 渠段运行示意图Fig.2 Schematic diagram of canal operation
2 结果与分析
2.1 不同闸门启闭速率下输水系统的水力特性
当输水流量变化时,为了保证输水系统的稳定性和输水工程的稳定安全,通常会通过调控节制闸启闭速率,使得渠道能够保持一个比较稳定的水位或一定的水位变率。
建立典型渠段的非恒定流数学模型,研究渠段输水流量由200 m3/s降至100 m3/s时,不同的闸门启闭速率下的水力过渡过程,渠段的上、下游闸门以0.01,0.02,0.05,0.1 m/min的速率同步调节。图3、图4为各断面的水位变化和流量变化曲线。

图3 各断面水位变化曲线Fig.3 Variation curve of water level of each section
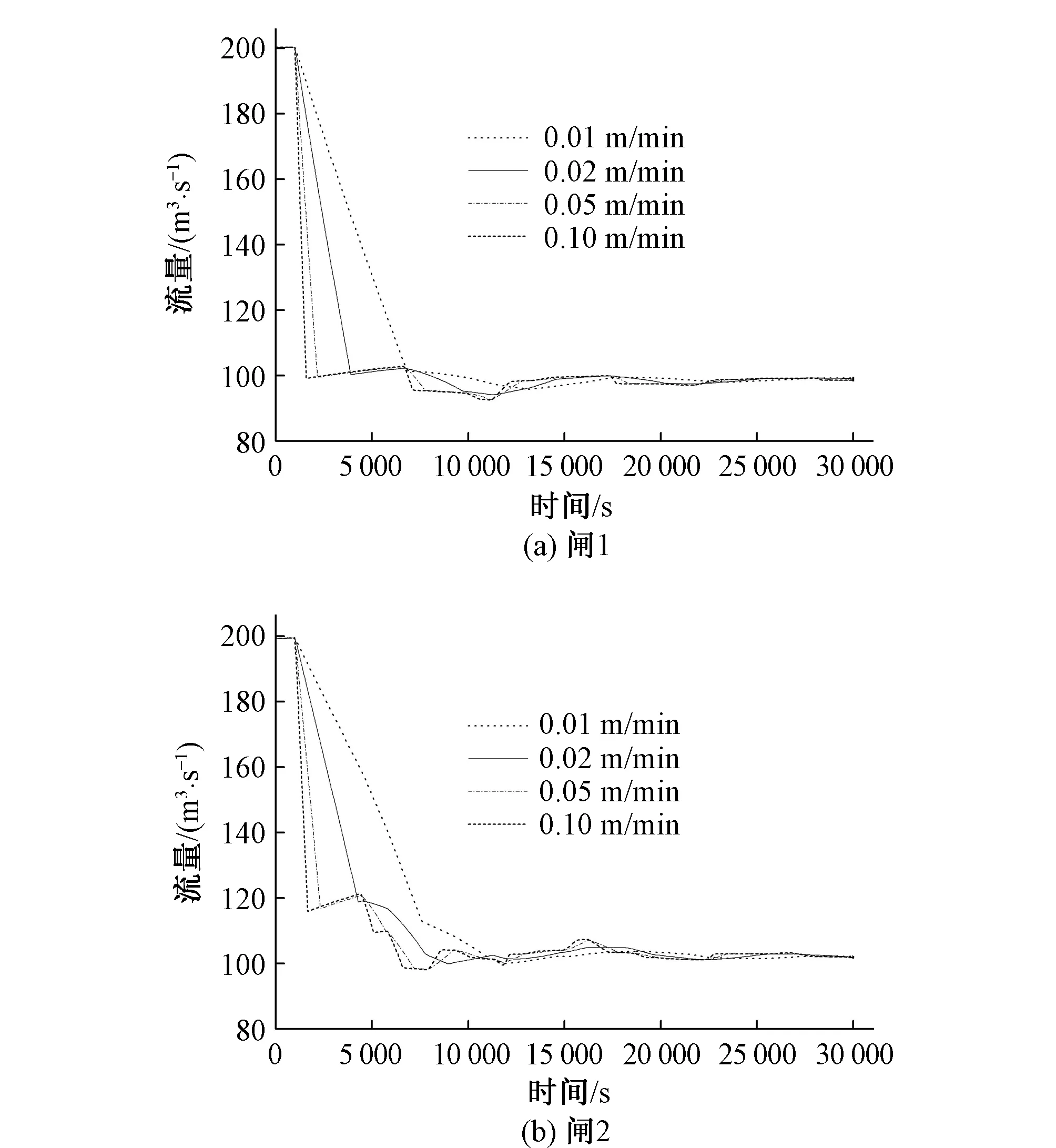
图4 过闸流量变化曲线Fig.4 Curve of water discharge through gate
由计算结果可知:
(1)闸门的启闭速率对渠段的水位波动、流量变化的影响比较显著。水位波动范围、流量变化速率与闸门的启闭速率呈正相关。即闸门的启闭速率越大,各断面的水位波动范围越大,流量变化速率越大,出现波动的时间越早,但同时各断面恢复到新的恒定流状态所需的时间越少。
(2)节制闸调控时会产生一定的干扰波,其传播需要一个过程,上下游闸操作时所产生的顺水波和逆水波在渠道内出现相互叠加、衰减或加剧的情况,这就导致两节制闸断面处的水位波动最大,渠道中间断面的水位波动要小且水位变化会滞后一段时间,并且在某些闸门启闭速率下中间断面的水位波动会比较混乱。
(3)当输水流量由200 m3/s降至100 m3/s,采用闸前常水位调控,闭门速度小于0.01 m/min时,渠段水位最大下降速率为0.137 m/h,水位波动变化速率能满足长江委规定的南水北调中线总干渠允许下降速率0.2 m/h的要求[9]。
2.2 水力震荡现象
在输水工程运行中,节制闸除了调节水位流量,还需担负事故情况下的挡水功能。例如当某渠段发生事故或上游渠段水质受到污染时,事故渠段两端的闸门可能需要在短时间内快速关闭防止事故的进一步发展。节制闸的突然关闭会引起水力振荡现象,并在渠道内产生壅水。本文模拟了典型渠段输水流量由设计流量变为零的工况,两端节制闸以相同的速度同时关闭。图5为模拟的各断面水位变化结果。图6为不同的闸门关闭速度时下游闸前水位变化过程。

图5 各断面的水位变化Fig.5 Variation curve of water level of each section

图6 不同闭门速率下的下游闸前水位Fig.6 Variation curve of water level before downstream gate of different closed rates
当渠段两端节制闸同时关闭时,渠道内流量必然会发生变化,渠道内的流量改变以移动波的形式进行传播。因此,两端节制闸处产生的顺行落水波和逆水波会不断地发生反射、交叉、重叠,并进行能量交换和传递,进而导致上下游水位交替升降现象的产生。
由图5、图6的计算结果可知:
(1)两节制闸突然关闭时,水位发生骤降和骤涨最大的断面分别位于上游闸门的下游断面和下游闸门的上游断面。当闸门调节速率为0.1 m/min时,水位下降最大值为1.217 m,水位上涨最大值为1.06 m。
(2)渠段水力震荡现象受闭门速率影响显著。当闸门闭门速率降低时,水力振荡现象会减弱,水位出现波动的时间延后,水位波动的幅度和水位的壅高均减小。
因此应尽量降低闸门的闭门速率,以减轻水力振荡现象的不利影响。
2.3 水流漫溢现象
当某一节制闸开度突然减小或关闭时,渠道内的一部分水量来不及排出,必然会在闸前产生一定程度的瞬态壅水,壅水达到一定程度时,某一断面的水位若超过渠顶高程,就会发生水流漫溢现象。
本文模拟了典型渠段以设计流量运行时,上游节制闸开度保持不变,下游节制闸以不同的闭门速率关闭时的水力过程。模拟结果如图7~图9所示。
由图7可以看出,当下游节制闸闸2逐渐关闭时,过闸流量逐渐减少为零,闸前水位开始抬升,并产生向上游传播的逆水波,从而引起渠段水位由下游向上游依次抬升,渠段末端水位最先达到渠顶高程,出现水流漫溢现象。由图8可知,发生溢流现象所需时间与闸门的闭门速率呈负相关,且当闭门速率达到一定值后,发生溢流现象所需时间趋于一定值。

图7 渠道各断面水位变化Fig.7 Variation curve of water level of each section
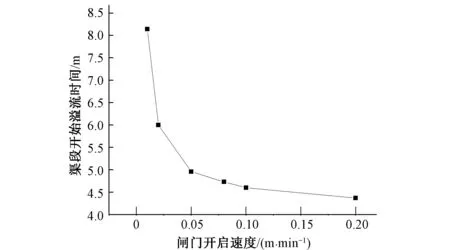
图8 漫溢时间与闸门开启速度的关系图Fig.8 Relation between time of overflow and open rate of gate
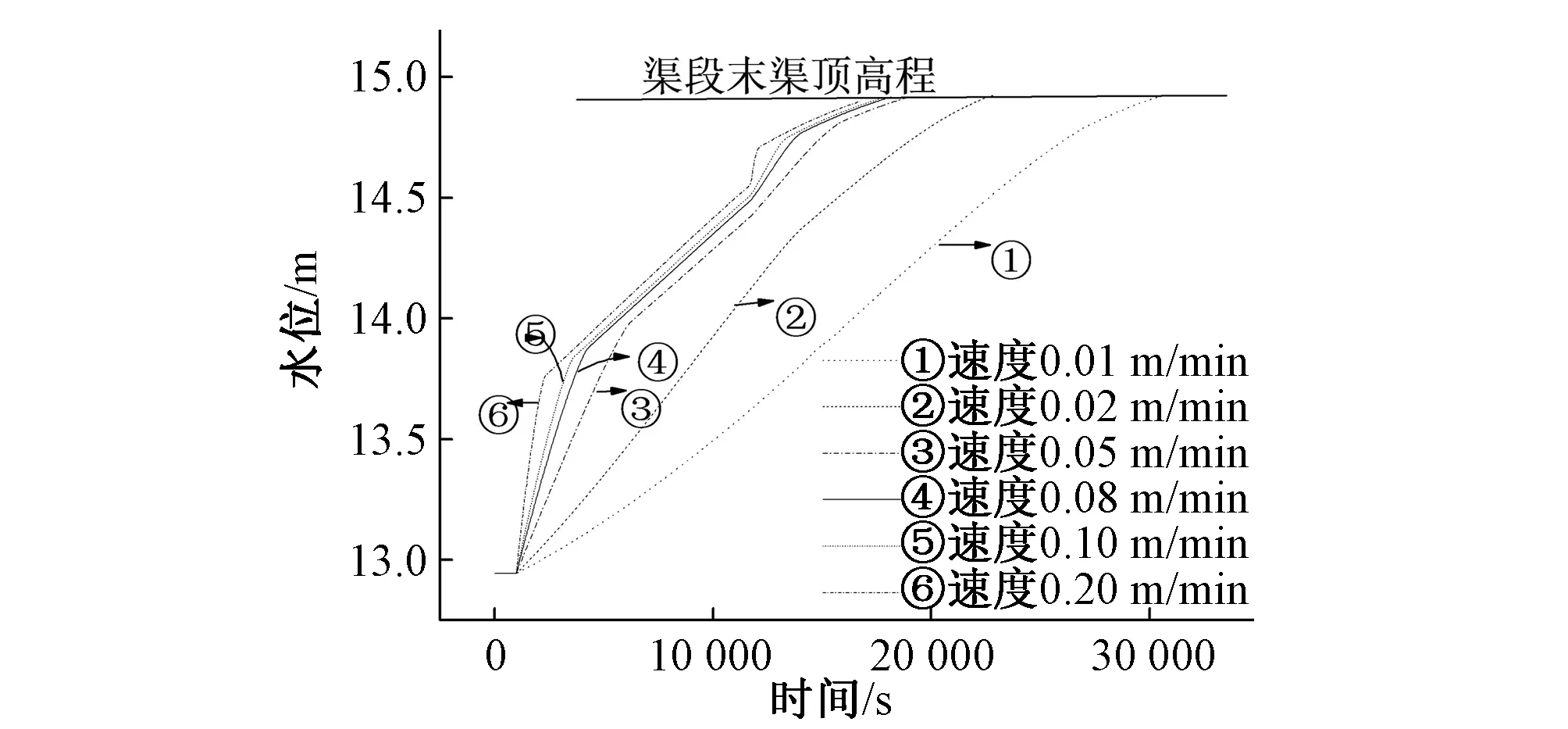
图9 不同闭门速度下的闸2闸前水位Fig.9 Water level before No.2 gate of different closed rates
图9为不同闸门闭门速度下的闸2闸前水位变化情况。可以看出,闸2的闸前水位变化分为两个阶段:第一阶段为闸门关闭过程中的水位变化曲线,闸前水位的变化速度随闸门的闭门速率增大而增大;第二阶段为闸门完全关闭后的水位变化曲线,此阶段不同闸门调节速度下的水位变化曲线基本平行,水位上涨速度大致相同,约为0.3 m/h。
因此,当输水系统需要关闭某一节制闸时,为尽量避免渠道出现漫溢事故,应尽量缓慢关闭闸门,延缓水流漫溢发生的时间,以争取更多的反应时间采取相应措施保证渠道的安全运行。
2.4 不同节制闸间距下输水系统的水力特性
节制闸间距的选取会影响到工程投资以及工程的安全运行。本节对不同节制闸间距下的水力特性进行比较分析计算,分别取10、20、25、30、40、50 km的节制闸间距,输水流量变化为200 m3/s降至100 m3/s,两端节制闸以0.05 m/min速度同步调节,采用闸前常水位控制模式。
(1)渠道响应时间。在渠道输水工程中,通常采用渠道的响应时间[10]来衡量渠道供水的及时程度。渠道的响应时间反映了输水调度的稳定性和速动性。渠道的响应时间越短,渠道的输水调度越灵活,渠道内的水流会在越短的时间内达到新的稳定状态。
当输水流量由200 m3/s降至100 m3/s时,不同节制闸间距下渠道的响应时间计算结果如表1所示。由表1可知,渠道的闸间距越大,渠道响应时间越长,达到新的稳定状态就越慢。

表1 不同节制闸间距下的渠道响应时间Tab.1 The channel response time of different interval of control gates
(2)闸前水位壅高。“是否会弃水”是衡量明渠输水工程的一个重要性能指标。当水量需求急剧减小时,渠道内的一部分水量可能会来不及排出而发生壅水;此外,闸门的启闭动作也会导致在闸前出现一定程度的壅水,再考虑风浪的影响,有可能导致渠道某一时刻的瞬时水位超过堤顶高程产生弃水。要使渠道在调控过程中不发生弃水或少弃水,就需要研究不同节制闸间距下的渠道安全超高。
安全超高包括风浪超高和水位壅高两部分。风浪超高可采用莆田试验站公式[11]计算得到,由此公式可知风浪超高与节制闸的间距、渠道过流量无关。因此,只需研究闸门动作所引起的水位壅高。不同节制闸间距对应的水位壅高计算结果见表2。显然,节制闸间距越大,水位壅高值越大,渠道就需要越大的安全超高来保证安全。

表2 不同节制闸间距下的闸前水位壅高Tab.2 The backup water level before gate ofdifferent interval of control gates
(3)事故排空时间。在输水工程管理运行过程中,当需要对某渠段进行检修维护时,需将该渠段内的水量排空。两节制闸的间距越小,渠道内的蓄水量越小,排空和检修所需的时间就越短。此外,如果输水渠道可能发生溃堤时,渠道内蓄水量的多少也将直接影响到事故损失的大小。因此,从安全性考虑,节制闸间距也不宜取得过长。本节计算了流量q=50 m3/s时,不同节制闸间距的排空时间,计算结果见表3。可以看出,节制闸间距越小,节制闸间的蓄水量越少,排空时间就越短。
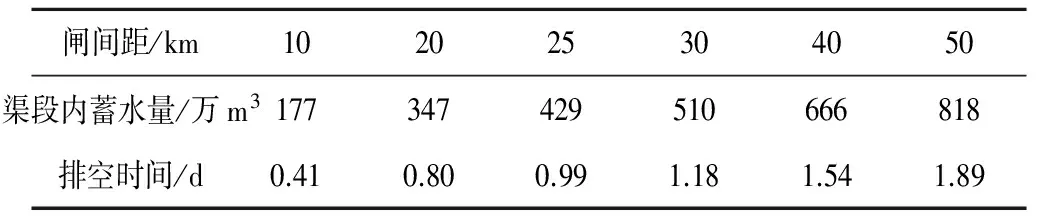
表3 不同节制闸间距下的排空时间Tab.3 The eliminating time of different interval of control gates
(4)建闸投资。对于一个长距离明渠工程,节制闸间距的选取直接关系到工程投资及运行后的管理成本。由于获取资料的限制,本文只是粗略地估算由于节制闸间距的不同而引起的投资差异情况。假设渠系陶岔首至黄河南段渠系总长480 km,不同节制闸间距下的建闸个数以及以30 km为闸间距时的节制闸投资为基础的投资比如表4所示。显然,闸间距越小,需建节制闸越多,投资越大。

表4 节制闸建闸个数与投资比Tab.4 The number and investment ratio of gate building
(5)节制闸间距影响综合分析。将节制闸间距与渠道响应时间、闸前水位壅高、排空时间、建闸投资比等参数的关系曲线绘于图10。由图10可知:闸前水位壅高、排空时间和渠道响应时间与闸间距呈单调递增关系,而投资比与闸间距呈单调递减关系。因此,通过综合分析比较,可得到最优节制闸间距为25~35 km。但在实际工程中,还应根据工程的具体地形地质条件、水力条件、当地经济社会情况等影响因素来综合确定。
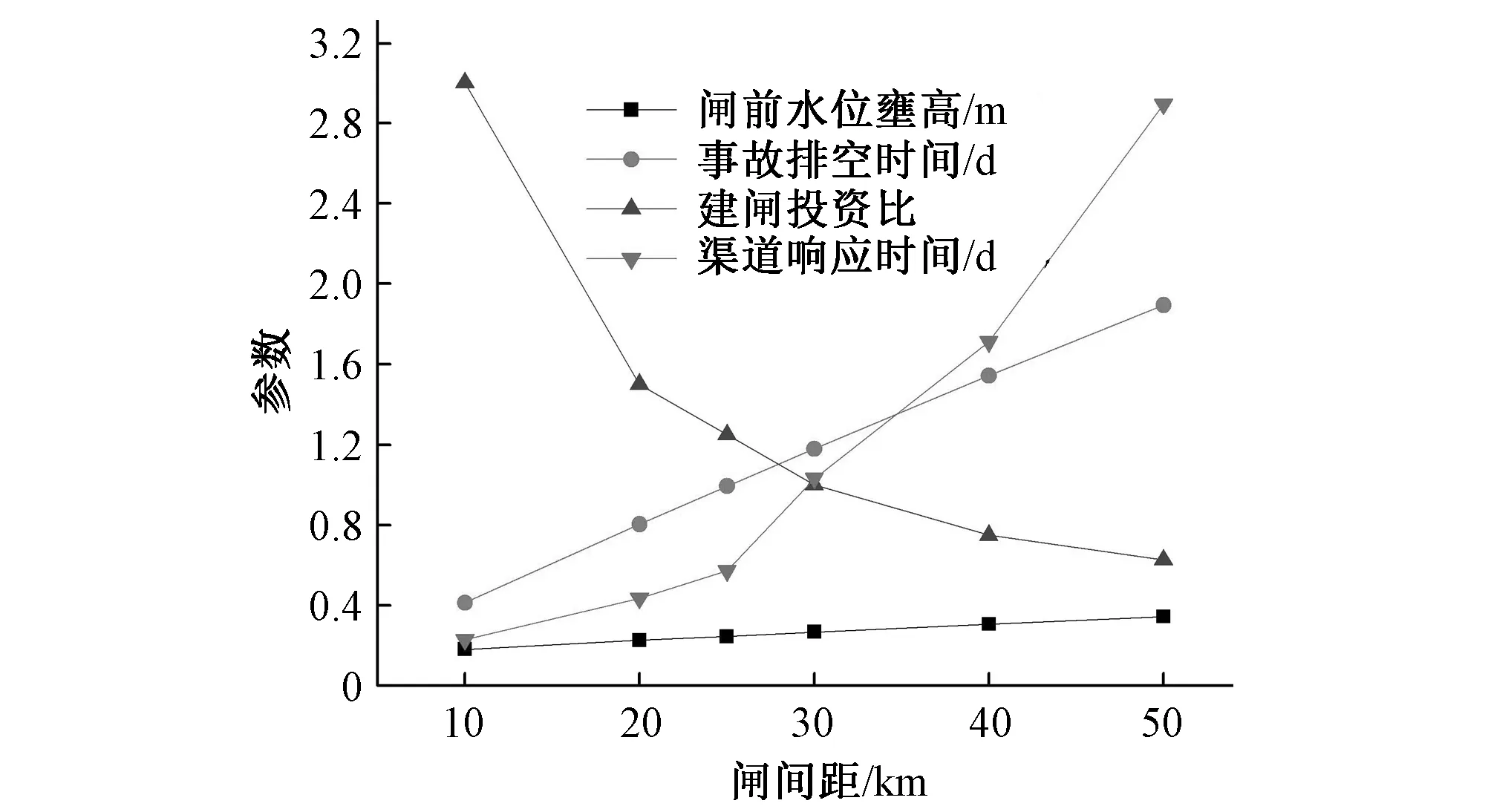
图10 不同节制闸间距下各参数Fig.10 Parameters of different interval of control gates
3 结 语
本文以南水北调中线总干渠的陶岔至黄金河段的渠首段为算例,分析了节制闸调控下的输水系统水力特性,得到以下结论。
(1)当流量变化相同时,水位波动范围、流量变化速率与闸门的启闭速率呈正相关。即闸门的启闭速率越大,水位波动范围越大,流量变化速率越大,且出现波动的时间越早,但同时各断面恢复到新的恒定流状态所需的时间越少。
(2)水力震荡现象受闭门速率影响显著。实际工程应以尽量降低闸门闭门速率,以减弱水力振荡现象,延缓水位出现波动的时间,降低水位波动的幅度,减小水位壅高。
(3)发生溢流现象所需时间与闸门的闭门速率呈负相关,且当闭门速率达到一定值后,发生溢流现象所需时间趋于一定值。实际运行时,应尽量缓慢关闭闸门,延缓水流漫溢发生的时间,以争取更多的反应时间采取相应措施保证渠道的安全运行。
(4)综合比较不同节制闸间距下的渠道响应时间、闸前水位壅高、事故排空时间、建闸投资比,认为南水北调中线渠首段明渠节制闸间距取在25~35 km之间最优。
□
[1] 杨开林.南水北调中线工程水力控制实时数字三维视景仿真[J].南水北调与水利科技,2004,2(1):1-3.
[2] 王 涛.神经网络渠道PID控制理论及其动态仿真研究[D].武汉:武汉大学,2004.
[3] 王长德.灌溉渠道水力自动闸门的运行稳定问题[J].武汉水利电力学院学报,1982,(4):25-33.
[4] 王长德,韦直林,张礼卫.上游常水位自动控制渠道明渠非恒定流动态边界条件[J].水利学报,1995,26(2):46-57.
[5] 王念慎,郭 军,董兴林.明渠瞬变流最优等容量控制[J].水利学报,1989,20(12):12-20.
[6] 王 涛,杨开林.调水工程系统的水力控制仿真与参数的优化[J].水利学报,2006,37(9):2 070-1 077.
[7] 韩延成.长距离调水工程渠道输水控制数学模型研究及非恒定流仿真模拟系统[D].天津:天津大学,2007.
[8] 吴泽宇,周 斌.南水北调中线渠道控制计算模型[J].人民长江,2000,31(5):10-11.
[9] 周 芳.调水工程中明渠输水系统的水力控制研究[D].天津:天津大学,2008
[10] 章晋雄,牛争鸣. 南水北调中线输水渠道系统的仿真研究[J].系统仿真学报,2002,14(12):1 588-1 590.
[11] 潘少华.江河风浪计算中的一些问题[J].人民黄河,1994,(7):13-16.
