基于Copula-Monte Carlo法的水库防洪调度多目标风险分析

陈 凯，彭 杨，吴志毅

(华北电力大学 可再生能源学院，北京102206)

0 引 言

水库防洪调度是减少洪灾损失的重要非工程措施。水库防洪调度需要考虑水库自身安全、上下游防洪目标和众多约束条件，是一个典型的多阶段、多约束的多目标决策问题。受流域降雨、洪水、工程状态等客观不确定性以及各种人为调度管理等主观因素的影响，有可能导致在防洪调度实际过程中，难以避免地出现实际调度结果不能达到预期调度目标，不仅影响水库汛期的安全稳定运行和水库综合效益的发挥，也会给调度决策带来一定的风险。因此，有必要进行水库防洪调度多目标风险分析。

自20世纪80年代初以来，我国学者已开始水库调度风险问题研究，提出了概率法[1]、一次二阶矩法[2]、事故树法[3]、蒙特卡洛随机模拟法[4]等解决方法。对于入库径流和洪水的不确定性带来的风险，常采用蒙特卡洛随机模拟法进行估算[4]。在水库防洪调度风险研究方面，李英海等[5]通过对三峡水库入库洪水预报误差进行随机模拟，并利用灰色关联法对防洪调度方案进行了风险决策。覃晖等[6]采用蒙特卡洛法对三峡水库入库径流进行随机模拟，并通过调度确定了防洪风险，并应用基于相对优势度的风险型多属性决策方法对各调度方案进行了评价。王丽萍等[7]通过对预报误差进行随机模拟来修正溪洛渡-三峡梯级水库的预报洪水，并通过建立的梯级防洪调度风险估计模型对梯级水库的防洪风险进行了分析。周研来等[8]采用Copula-MC法对万家寨水库上游区间洪水进行了模拟，并与干流洪水叠加组成了万家寨水库的入库洪水，通过对水库汛限水位动态控制分析了各调洪方案的风险。而当水库下游与防洪控制区之间有支流汇入时，支流来水的不确定性也会对下游防洪控制区带来一定的风险。闫宝伟等[9,10]考虑干支流来水不确定性，利用Copula函数建立联合分布，分析了长江与清江洪水发生时间与发生量级的遭遇风险。刘章军等[11]利用Copula-MC法通过对干支流洪水进行随机模拟，通过水库调洪函数计算了隔河岩水库下游高坝洲断面的洪水概率分布。上述学者虽考虑了干支流洪水的不确定性，但却没有结合水库调度对风险进行进一步分析。

本文考虑干支流洪水的不确定性对水库防洪调度的影响，提出了一种基于Copula-MC法的水库防洪调度多目标风险分析方法。将该方法应用于向家坝水库防洪调度风险分析中，给出兼顾上下游防洪目标要求的最优调度方案，为水库汛期防洪调度决策提供参考。

1 水库防洪调度多目标风险分析

本文考虑入库流量和区间支流流量的相关性，采用Copula-MC法对干支流洪水同时进行模拟，在对模拟洪水进行防洪优化调度的基础上，计算不同调度方案的防洪目标值与风险率，并采用基于组合权重的理想点法对调度方案进行风险决策，给出最优调度方案。整个防洪调度多目标风险分析的过程如图1所示。

图1 防洪调度多目标风险分析流程图Fig.1 Flowchart of multiobjective risk analysis for flood control operation

1.1 干支流洪水随机模拟

当水库下游有支流汇入时，下游防护区的安全需在调度过程中同时兼顾区间来水，故本文考虑入库洪水和区间来水之间的相关性，利用Copula-MC法对干支流洪水同时进行模拟。

一般情况下，干支流洪水间既存在着随机性又有相关性，可采用Copula函数描述干流洪峰X和支流洪峰Y的联合分布[9]。由Sklar定理[12]可知，一个二维联合分布可以由两个独立的边缘分布和一个Copula函数构成。设干流洪峰X和支流洪峰Y的边缘分布分别为u=FX(x)和v=FY(y)，可采用P-Ⅲ型分布[13]对它们进行描述。采用Clayton Copula函数[14]作为联接函数，则干支流洪峰的联合分布可表示为：

C(u,v)=(u-θ+v-θ-1)-1/θ

(1)

式中：θ为Copula参数，可根据与Kendall秩相关系数的关系求出[14]。

随机变量X和Y之间存在相关性，由Monte Carlo产生的二维随机数须保持相应的相关性。鉴于边缘分布u和v是服从[0,1]的均匀分布，则支流洪峰为某一定值时干流洪峰的条件分布为：

C(u|v)=[1+vθ(u-θ-1)]-(1+θ)/θ

(2)

由于条件分布C(u|v)也服从[0,1]之间的均匀分布，因此采用Copula-Monte Carlo方法对干支流洪峰进行随机模拟的基本思路为：首先由计算机产生二维随机数m1和m2，令v=m1；然后通过求解方程m2=C(u|v)得到u；u和v分别为两随机变量不超过某值的概率，可通过二者的边缘分布推求出X和Y的随机数值。

根据上述方法可推求出干支流洪水的洪峰流量，然后选取相应的典型洪水放大得到各自的洪水过程。

1.2 防洪优化调度

水库防洪任务主要有三类，即保证坝体自身的安全、减轻下游洪涝灾害和减少上游淹没损失。本文主要考虑水库自身安全和下游防洪控制区的安全，选取最高坝前水位最低和下游防洪控制区最大流量最小为目标函数，建立防洪优化调度模型，其目标函数为

Zm=min[maxZ(t)]

(3)

qm=min{max[Qck(t)+Qqj(t)]}

(4)

式中：Z(t)表示各时段的坝前水位；Qck(t)表示水库各时段的下泄流量；Qqj(t)表示区间洪水的各时段流量。

约束条件：主要包括水量平衡约束、最大泄流能力约束、调度期末水位约束、下泄流量约束、水位库容约束及防洪调度规程等[15]。

在防洪调度准则和约束条件的限制下，可利用权重协调法[16]将多目标优化问题转化为单目标优化问题，进而利用动态规划法进行求解，得到非劣解集。

1.3 风险率推求

在考虑干支流来水不确定性的情况下，不同调度方案的防洪目标值及其带来的风险是决策者们所关心的最重要的问题。因此有必要对每一种方案进行风险估计，确定不同目标突破安全阈值的风险率。

将上述随机模拟得到的干支流洪水序列作为防洪优化调度模型的输入条件，通过求解可得到不同方案下(即非劣方案)坝前最高水位系列Zm和下游防洪区最大流量序列qm，分别统计坝前最高水位超出安全阈值(防洪高水位)和下游防洪区组合流量超过安全阈值(防洪控制点安全过流量)的次数，计算其越限的概率，即为防洪控制区的出险率和水库自身的出险率。

1.4 基于组合权重的理想点法多目标风险决策

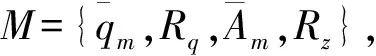
多目标非劣方案的综合评价方法有很多，但在水库防洪运用中，为追求防洪效益最佳，应尽可能选取能够反映目标值与最优值接近程度的评价方法，其中理想点法[17]不失为一种切实可行的方法。由于各个目标的相对重要程度不同，可将各指标的权重系数与评价方法相结合，综合考虑各目标的主客观权重，建立起基于组合权重的理想点法，对非劣解进行排序，选出令决策者满意的方案。整个决策过程主要分为两步：首先通过层次分析法和熵权法[18]分别获得主观权重wzj和客观权重wkj，然后将主客观权重进行组合[19]，得到组合权重wj=αwzj+(1-α)wkj，其中α代表决策者对主观经验和客观数据的偏好程度；然后将根据组合权重，采用理想点法[20]对各方案进行排序，选出最优方案。

2 实例应用

向家坝水库是金沙江水电开发基地的最后一级，工程开发任务以发电为主，同时改善上、下游通航条件，结合防洪拦沙，兼顾灌溉，并对溪洛渡水库起反调节等作用。水库正常蓄水位380.00 m，死水位和防洪限制水位均为370.00 m，总库容51.63 亿m3，调节库容和防洪库容均为9.03 亿m3，具有季调节性能。水库汛期不仅可以与溪洛渡水库联合运用，提高下游川江河段沿岸宜宾、泸州、重庆等城市的防洪标准，还可以配合三峡水库运用为长江中下游地区发挥积极的防洪作用。水库下游左岸有长江一级支流岷江的汇入。由于岷江是长江流域水量最大的支流，汛期暴雨洪水活动频繁，与金沙江洪水遭遇后，会增加水库下游李庄防洪控制点的风险。

分别选取屏山站和高场站1951-2010年实测流量资料和历史特大洪水资源来拟合金沙江洪峰和岷江洪峰的边缘分布。采用年最大法取样，分别得到这两个站的洪峰流量序列，其边缘分布可用PIII型分布函数表示，采用线性矩法估计参数，并采用χ2检验方法进行假设检验，结果如表1所示。

表1 P-Ⅲ型分布参数及检验结果Tab.1 Parameters and hypothesis test results ofP-Ⅲ margin distributions

由表1可见，在5%的显著性水平下，自由度为k-r-1的χ2检验的结果均小于临界值(表示括号中数据为检验的临界值)，落在接受域内，因此这2个站的P-Ⅲ型分布都通过假设检验。经统计计算可得金沙江和岷江洪水洪峰的秩相关系数为τ=0.123，由此可根据文献[14]推出Clayton Copula函数的参数θ=0.28。

采用上述Copula-Monte Carlo方法，可以得到10 000组金沙江洪水和岷江区间洪水的洪峰流量，如图2所示。选取1998年8月份洪水为典型洪水，根据同倍比原则按照洪峰进行放大，即可得到模拟的金沙江和岷江相应的10 000场洪水过程。

图2 干支流洪水洪峰随机模拟值Fig.2 Simulated flood peaks of mainstream and its tributary

将模拟得到的10 000场金沙江洪水和岷江洪水带入防洪优化调度模型式(3)和式(4)中，通过求解可以得到非劣解方案，每个解都可用其目标均值来表示，如图3所示。

图3 向家坝防洪优化调度非劣解集Fig.3 Pareto solutions of flood control optimal operation in Xiangjiaba reservoir

向家坝水库防洪运用时，下游防洪控制区李庄的安全流量是40 000 m3/s，水库自身的安全水位为380 m。根据计算得到的9组非劣调度方案，统计两目标各自超过其安全阈值的次数，即可得到防洪控制区的出险率和水库自身的出险率。表2给出了各非劣方案的防洪目标均值与相应的风险率。

由表2可见，从方案一至方案九，防洪控制区的最大流量呈逐渐降低的趋势，其风险率也随之减小，而坝前最高水位逐渐升高，其风险率呈现出非减的趋势。其中，方案一的下游防洪区的风险最高且最大下泄流量最大，方案九的坝前水位最高，且对于水库自身防洪具有一定的风险。

将表2中防洪目标的均值和风险率作为原始评价指标，同时将各指标均视为成本型指标，根据文献[17]中的标准0～1变换对其进行归一化处理，可得到标准化指标矩阵：

表2 各防洪调度方案目标均值及风险率Tab.2 Objective mean value and risk of different floodcontrol operation scheme

方案防洪区最大流量均值/(m3·s-1)风险率/%坝前最高水位均值/(m3·s-1)风险率/%一32921．4212．72370．260．02二32768．1412．33370．390．02三32582．6111．76370．550．03四32384．1511．25370．770．03五32098．7410．31371．090．03六31748．899．12371．620．18七31448．347．73372．430．61八31043．556．27374．092．01九30676．124．70376．074．19

采用熵权法可以得到各评价指标的客观权重，对于主观权重，依据侧重下游防洪区安全、侧重水库自身安全两种偏好给出两组主观权重。将主客观组合因子皆取为0.5，则可得到不同侧重对象下的组合权重，具体见表3。

表3 评价指标权重Tab.3 Weights of different evaluation index

据此采用理想点法对各组调度进行排序，具体结果见表4。

由表4可见水库自身的风险率和风险损失较低，最优方案基本集中在中下部，表明排序结果合理。根据侧重下游安全、侧重水库安全两种决策偏好不同，最优有所差别，当侧重水库下游安全时，下游最大下流流量较小的方案八更优；侧重水库自身安全时，坝前水位较低且最大下泄流量不大的方案七更优。因此，决策者可以根据自己的主观偏好给予各目标不同的权重，最终决策出的方案必定是一个综合协调了下游安全和水库自身安全的均衡解。

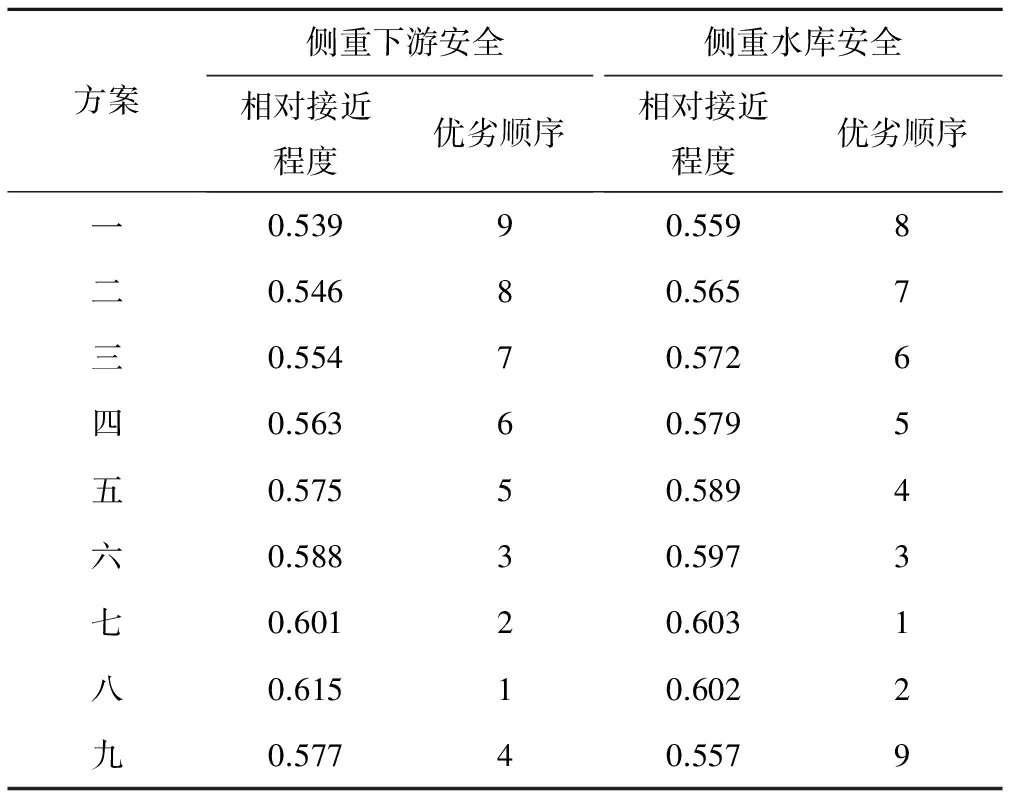
表4 各调度方案优选排序结果Tab.4 Ranking results of each operation scheme

3 结 语

本文以向家坝水库为研究对象，以干支流洪水不确定性作为对防洪优化调度过程中的主要风险因子，采用Copula-Monte Carlo法对其进行定量描述，在对模拟洪水进行防洪优化调度的基础上，对不同调度方案的防洪目标值与风险进行计算，并采用基于组合权重的理想点法对调度方案进行风险决策，选出最优调度方案。结果表明：①所建模型能对水库汛期干支流洪水不确定性给向家坝水库给上下游防洪带来的风险进行估计、评价和决策，有助于决策者制定出效益与风险均衡的防洪调度决策方案；②水库下游防洪控制区的过流量越小，其超过安全泄量的风险也越小，但水库坝前最高水位会增加，且最高坝前水位超过防洪安全水位的风险也会增加，因此，控制下游防洪区的过流量，势必会以增加水库自身的防洪风险为代价；③针对决策者的主观倾向不同，其决策出的最优方案也会有差异，评价时需谨慎处理下游防洪区安全和水库安全两个目标之间的矛盾。

□

[1] 傅 湘,王丽萍,纪昌明. 洪水遭遇组合下防洪区的洪灾风险率估算[J]. 水电能源科学,1999,(4):23-26.

[2] 曾玉红,胡敏良,梁在潮. 防洪系统风险分析及其预报阈值研究[J]. 武汉大学学报(工学版),2003,(6):27-30.

[3] 程卫帅,陈 进. 防洪体系统风险评估模型研究[J]. 水科学进展,2005,(1):114-120.

[4] 刁艳芳,王本德. 基于不同风险源组合的水库防洪预报调度方式风险分析[J]. 中国科学:技术科学,2010,(10):1 140-1 147.

[5] 李英海,周建中,张勇传,等. 水库防洪优化调度风险决策模型及应用[J]. 水力发电,2009,(4):19-21,37.

[6] 覃 晖,李清清,周建中. 基于相对优势度的水库防洪调度多属性风险决策方法研究[J]. 长江科学院院报,2011,(12):58-63.

[7] 王丽萍,黄海涛,张验科,等. 梯级水库群联合防洪调度风险估计模型[J]. 中国农村水利水电,2014,(1):69-72,76.

[8] 周研来,梅亚东. 基于Copula函数和Monte Carlo法的防洪调度风险分析[J]. 水电能源科学,2010,(8):37-39.

[9] 闫宝伟,郭生练,陈 璐,等. 长江和清江洪水遭遇风险分析[J]. 水利学报,2010,(5):553-559.

[10] 闫宝伟,郭生练,余 维. 长江和清江洪水过程遭遇风险分析[J]. 水力发电学报,2013,(1):50-53.

[11] 刘章君,郭生练,胡 瑶,等. 基于Copula-Monte Carlo法的水库下游洪水概率分布研究[J]. 水力发电,2015,(8):17-22.

[12] Nelsen R B. An introduction to Copulas[M]. Springer, New York, 1999.

[13] 中华人民共和国水利部. 中华人民共和国水利行业标准:水利水电工程设计洪水计算规范[M]. 北京：中国水利水电出版社, 2006.

[14] 郭生练,闫宝伟,肖 义,等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文,2008,(3):1-7.

[15] 陈森林. 水电站水库运行与调度[M]. 北京:中国电力出版社, 2008.

[16] 贾本有,钟平安,陈 娟,等. 复杂防洪系统联合优化调度模型[J]. 水科学进展,2015,(4):560-571.

[17] 刘 方. 水库水沙联合调度优化方法与应用研究[D]. 北京：华北电力大学,2013.

[18] Liping Wang，Yanke Zhang, Changming Ji, et al. Risk calculation method for complex engineering system [J]. Water Science and Engineering, 2011,4(3):345-355.

[19] 王汉斌,杨 鑫. 一种基于AHP-RS的组合权重确定方法[J]. 中国安全生产科学技术,2010,(6):155-160.

[20] 方志耕,刘思峰. 决策理论与方法[M]. 北京:科学出版社, 2009.