基于突变理论的北京市水资源安全分析

谢开杰，李继清

(华北电力大学 可再生能源学院，北京 102206)

0 引 言

水资源是人类社会赖以生存和发展的重要物质资源。随着人口增长和社会经济不断发展，水资源短缺形势越发严峻，水资源安全问题日益成为人类社会关注的焦点问题之一。广义的水资源安全，是指水资源对国家的可持续发展具有良好的支撑和保障能力[1]。具体到某一区域，则指可供水资源量要满足其正常发展所必需的水量，又不致产生洪涝灾害，社会经济和生态环境才能维持可持续发展。因此，水资源安全问题研究对区域水资源的合理开发、高效利用和综合管理具有重要意义。

近年来，很多学者对水资源安全问题进行了不同层次的研究，主要包括水资源安全定义、评价指标体系以及评价模型的建立。郦建强[2]等提出水资源系统的状态稳定和功能健全是水资源安全的标志，其安全状况与水资源承载状况、水环境承载状况、水生态安全状况和经济社会的供水保障状况有关。Van Leeuwen[3]等通过分析水资源系统特性，提出了水资源压力指数和水资源安全指数的概念，并基于此建立了水资源安全评价指标体系。贾绍凤[4]等利用包含水资源状况、社会、经济和生态四方面因素的水资源安全评价指标体系，对海河流域水资源安全现状进行了评价，分析了造成海河流域水资源安全问题的主要原因。Schneider[5]等提出从水资源容量的角度衡量水资源安全，并建立了水资源供需平衡指标来分析流域水资源安全程度。高媛媛[6]等采用改进的层次分析法和基于因子分析的聚类分析法，对福建泉州2008年的水资源安全状况进行了评价，并分析了2000-2008年泉州市的水资源安全变化趋势。Lu[7]等采用基于模糊集理论的水安全评价方法对成都的水资源安全形势进行了评价，计算得到成都市水安全保障指数和水环境压力指数。

北京是水资源严重匮乏的特大城市，近年来，北京地区上游来水量大幅下降，深层地下水资源日益枯竭，然而城市规模扩大、人口增长、社会发展和居民生活水平的不断提高使得城市用水刚性需求持续增长。保障社会经济稳定发展和人民生活水平有赖于水资源的支撑，在资源禀赋不佳的情况下进行合理的水资源管理是北京市城市发展的重中之重，因而寻求保障城市发展的水资源安全阈值具有重要意义。本文应用突变理论，建立了北京市水资源安全尖点突变模型，应用突变评价法对模型变量进行量化归一，得出了保障北京市水资源安全的水量供需差值。同时，利用灰色系统模型对北京市2020年和2030年的需水量进行了预测，并结合北京市近30年来的供水状况，在特定供水保证率下对北京市2020年和2030年的用水安全状况进行了评估。

1 水资源安全分析突变模型

1.1 突变理论

突变理论最初由法国数学家Rene Thom创立，是一门研究由渐变引起突变的系统理论。它通过简洁的数学模型(研究对象的势函数)研究变化交界处的奇异性态，可用于分析复杂的系统行为。系统的势函数可以表示系统的任一状态，不同状态的取值取决于状态变量和控制变量的变化。通过研究系统的势函数，可以直接分析其临界点附近的不连续特征，使得突变理论尤其适用于研究内部机理尚不明了的系统。

水资源系统安全问题涉及的变量繁多，且安全性评价指标和方法不一，难以客观评价系统处于稳定连续状态还是突变状态；此外，水资源系统危机发生的机理符合突变理论的一般性特征，在水资源系统中，若水资源供需差值不在保障区域稳定发展的合理区间内，则可能会导致其发展状态的破坏，即发生突变。因此，适宜将突变理论用于水资源安全分析。近年也有不少学者将突变理论用于水资源系统的分析评价当中。孙雪峰[8]等将突变理论应用于水生态系统的分析，建立了水生态系统的尖点突变模型，用于水生态系统状态的判断、预警、改善和规划。李继清[9]等应用突变评价理论，通过构建长江流域洪灾综合风险评价指标体系，对长江流域1995-2000各年的洪灾综合风险进行了评估。Chen[10]等建立了城市水资源可持续利用水平突变评价模型，并对大连市进行了水资源可持续利用评估。尖点突变模型是常用的、最易被人接受的突变模型，通过构建水资源安全的尖点突变模型，能够客观地把握水资源安全状态与其影响因子之间的响应模式，判断水资源安全情势，从而能科学合理地进行水资源管理。

1.2 水资源安全分析尖点突变模型

尖点突变模型的势函数由一个状态变量x和两个控制变量u，v组成，其标准型为：

V(x)=x4+ux2+vx

(1)

式中：x为系统状态变量；u、v分别为系统的主、次控制变量。

势函数的临界点由V′(x)=0决定，该方程的几何图形是一个曲面，称为势函数的平衡超曲面(如图1),即：

4x3+2ux+v=0

(2)

对势函数(1)二次求导，得到奇点方程为：

12x2+2u=0

(3)

联立式(2)、式(3)消去x得到分歧集方程为：

B=8u3+27v2=0

(4)

通过图1的平衡超曲面，可以更为直观地理解突变的机理。平衡超曲面在平面上的投影即分歧集B，超曲面上的点在折叠曲线的边缘位置发生突跳，随着控制变量的变化，平衡超曲面逐渐发生扭曲并产生折叠。最终，在超曲面上形成了3个可能的平衡位置，上下两部分是稳定的，中间部分产生突跳，是不稳定的。跨越中间的折叠线，系统状态就会发生突变，据此便可判断突变是否发生，即突变判别式Δ=8u3+27v2<0时，系统发生突变。因此，水资源安全尖点突变模型的目标就是找出这个突变的区间Δ<0,从而进行系统管控，防止突变的发生。

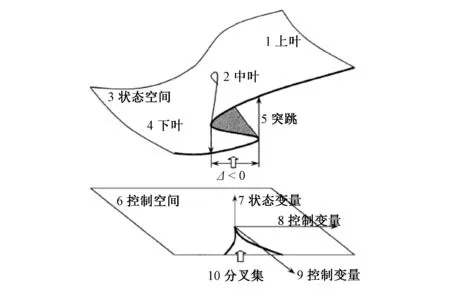
图1 尖点突变平衡超曲面 Fig.1 Cusp catastrophe hypersurface

1.3 水资源安全突变模型变量分析

建立水资源安全分析的突变模型，首先要确定模型的状态变量和控制变量。

突变模型的状态变量应反映水资源与经济发展指标的匹配程度及其对进一步发展的支撑能力。在区域水资源发展特性分析的基础上,可在水资源及其利用、区域发展和生态环境状况三个方面选取指标，分析区域发展的水资源支撑能力，即“水资源与社会经济发展协调度”指标。本文选取的三方面的指标包括：综合反映区域发展水资源条件的人均水资源量、反映水资源开发利用程度对区域社会经济发展支撑能力的人均供水量、反映区域经济发展富裕程度的人均GDP和反映水资源对农业发展和粮食生产保障能力的人均耕地面积，以及反映水资源对生态环境良性发展保障能力的单位面积产水量。水资源与社会经济发展协调度层次模型如图2。

图2 水资源与社会经济发展协调度层次模型Fig.2 Hierarchical model of the coordination between water resources and soci-economic development

突变模型的控制变量主要表征水资源系统的变化，而水资源系统是以水量和水质为基础的，因此，主、次控制变量可分别选为水量指标集合和水质指标集合。在选取具体的水量、水质指标时，应综合考虑对经济、社会和水生态发展产生影响的多方面因素，本文选取的指标包括：人均水资源量、降雨量和单位面积产水量；人均供水量、万元GDP耗水量和灌溉率；再生水

利用量和环境用水量；污水处理率和化学需氧量排放量；污染河长比和城市绿化覆盖率。图3给出了水资源安全突变分析控制变量的层次模型。水量指标方面，自然条件指标是区域水资源先天条件的直接体现，最能反映区域水资源的丰枯状况；社会经济指标反映了区域经济发展状况和水资源开发利用状况，直接关系到城市生产和生活用水安全；生态安全是水资源安全的重要方面，但对水资源系统整体安全的作用受自然条件和社会经济条件的影响，因此将自然条件指标和社会经济指标置于水量指标集合中的优先位置。水质指标方面，废、污水处理是保障区域水体不受污染最为重要的途径，对防止区域水质恶化起着关键性作用，因此将污水处理指标置于水质指标集合中的优先位置。

在突变模型状态变量和控制变量层次模型的基础上，采用突变评价法对各层指标进行量化递归运算，最终得到最上层指标的值。进行归一运算时，由于各指标的量纲不同，需要对实际指标值进行规范化处理，得到各指标的突变隶属函数值。规范化公式如下：

图3 水资源安全分析控制变量层次模型 Fig.3 Hierarchical model of the control variables in water security analysis

对正向型指标：X′i=(Xi-Xmin)/(Xmax-Xmin)

(5)

对负向型指标：X′i=(Xmax-Xi)/(Xmax-Xmin)

(6)

式中：X′i为各指标规范化后的值；Xi为各指标实际值；Xmax和Xmin分别为各指标逐年的最大值和最小值。

突变理论的特点是根据系统的势函数将系统的临界点分类，研究分类临界点附近非连续变化状态的特征，从而归纳出若干个初等突变模型[11]。进行综合评价时，根据评价指标的个数，常用的突变模型有以下3种：单个评价指标(a)的折迭突变；2个评价指标(a,b)的尖点突变；3个评价指标(a,b,c)的燕尾突变。通过前述分歧方程的分解形式可导出突变理论的归一公式，归一公式将系统内部各评价指标的不同质态归化为可比较的同一种质态，运用归一公式，可求出表征系统总体特征的总突变隶属函数值，即最上层指标值。以上三种突变模型的归一公式如下[12]：

Xa=a1/2

(7)

Xa=a1/2,Xb=b1/3

(8)

Xa=a1/2,Xb=b1/3,Xc=c1/4

(9)

计算出X值后，根据同一子系统中各指标是否互补，即各指标的作用是否相互关联，分别采用“大中取小”或“取平均值”原则得到上层指标的值。

2 实例研究

北京市人均水资源量不足200 m3，远低于世界公认的人均水资源量1 000 m3的缺水警戒线，不足全国平均水平的1/10。为满足城市供水需求，北京市常年超量开采难以补充恢复的深层地下水，造成了一系列生态环境问题，与此同时，社会经济不断发展，城市生产和生活用水需求居高不下。为保障北京市经济社会的正常运行，寻求水资源安全阈值可为水资源管理提供依据。

2.1 突变模型状态变量和控制变量计算

计算北京市水资源与社会经济发展协调度时，各指标的协调度是相对于全国平均水平设定的，计算公式如下[13]：

Wj=Wpj/Wp,Oj=Ocj/Oc,Cj=Wj/Oj

(10)

式中：Wj为北京市人均水资源相对指数；Wpj为北京市人均水资源量；Wp为全国人均水资源量；Oj为北京市其他指标(人均GDP，人均耕地面积，人均供水量和单位面积产水)相对指数；Ocj为北京市(人均GDP，人均耕地面积，人均供水量和单位面积产水)指标；Oc为全国(人均GDP，人均耕地面积，人均供水量和单位面积产水)指标；Cj为协调度指标。

由中国统计年鉴和北京市统计年鉴查得全国和北京市2001-2014年各指标值，根据公式(10)计算得各指标协调度，规范化后根据突变评价归一公式进行逐层量化递推运算。北京市2001-2014年各指标协调度和水资源与经济社会发展协调度计算结果如表1。以2001年为例，最下层各指标规范化值分别为：0.08，0.23，0.10，1.00，则中层3类指标值分别为：0.081/2=0.28，min(0.231/2,0.11/3)=0.46，1.001/2=1.00。区域发展指标、水资源利用状况指标和生态环境状况指标构成燕尾突变，由于任一方面的缺陷都会导致区域总体水资源支撑能力的破坏，因此应采用“大中取小”原则，则2001年北京市水资源与社会经济发展协调度为：min(0.281/2,0.461/3,1.001/4)=0.53。

由北京市水资源公报和北京市统计年鉴查得北京市2001-2014年水量、水质指标值分别如表2、表3。

以2001年水量指标为例，最下层各指标分别构成燕尾突变、燕尾突变和尖点突变，中层自然条件指标、社会经济指标和生态安全指标相互影响，构成燕尾突变。最下层各指标规范化后的值分别为：0.43，0.05，0.13，1.00，0，0.67，0，0，则中层3类指标值分别为：(0.431/2+0.051/3+0.131/4)=0.54，min(1.001/2,01/3,0.671/4)=0，(01/2+01/2/2)=0，2001年水量指标归一化值为：

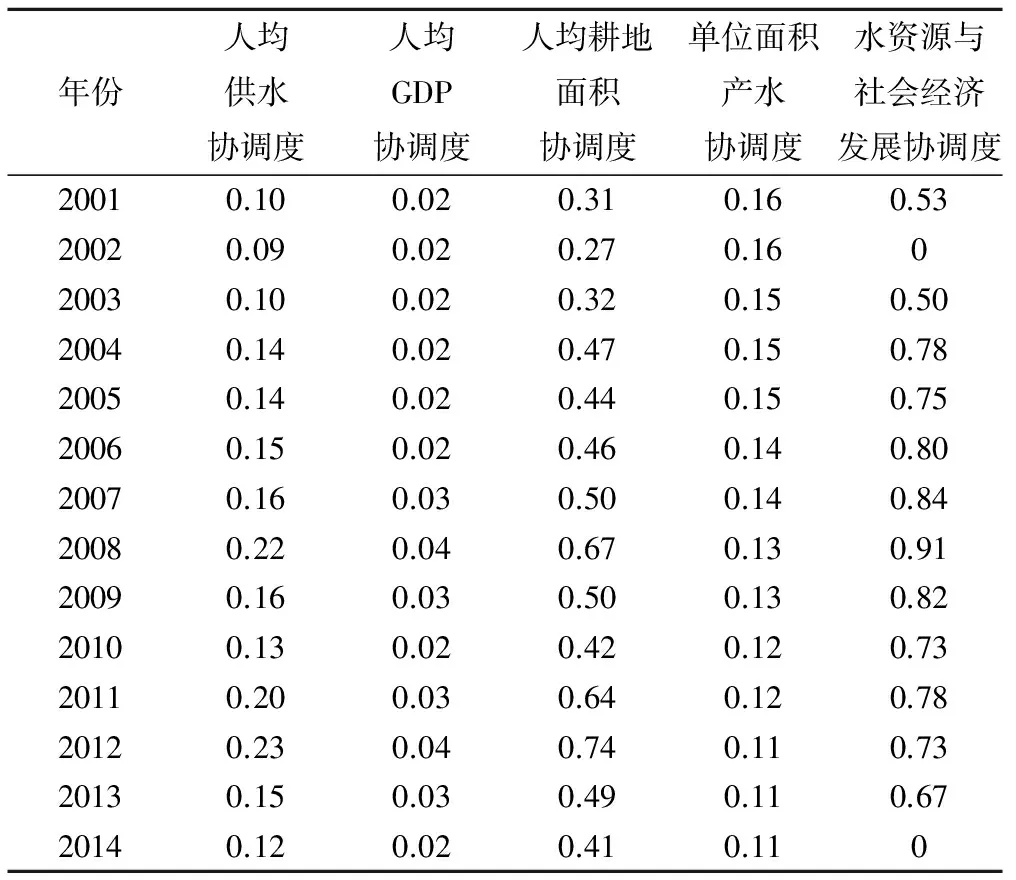
表1 北京市2001-2014年水资源与社会经济发展协调度Tab.1 Values of coordination between water resources andsoci-economic development of Beijing from 2001 to 2014

表2 北京市2001-2014年水量指标值Tab.2 Water quantity index set of Beijing from 2001 to 2014

(0.541/2+01/3+01/4)/3=0.25，以此类推，可得2001-2014年北京市水量、水质指标归一化值如图4。

2.2 水资源安全突变分析

水资源安全突变分析的目的是通过建立表征水资源安全状态的变量(状态变量)与其影响因子(控制变量)之间的关系，探寻水资源状况对社会经济发展的影响规律，判断水资源安全系统是否存在突变的威胁。

由尖点突变的平衡曲面4x3+2ux+v=0变换可得：

4x3=-2ux-v

(11)

式中：x为水资源系统安全尖点突变模型状态变量即水资源与社会经济发展协调度；u为尖点突变模型主控制变量即水量指标；v为次控制变量即水质指标。

令y=4x3,u=k1u′,v=k2v′-k3，则平衡曲面拟合式为：

y=k1(-2u′x)+k2(-v′)+k3

(12)

式中：u′为水量指标归一化值；v′为水质指标归一化值。

上式用矩阵表示即：

Y=XB

(13)

表3 北京市2001-2014年水质指标值Tab.3 Water quality index set of Beijing from 2001 to 2014

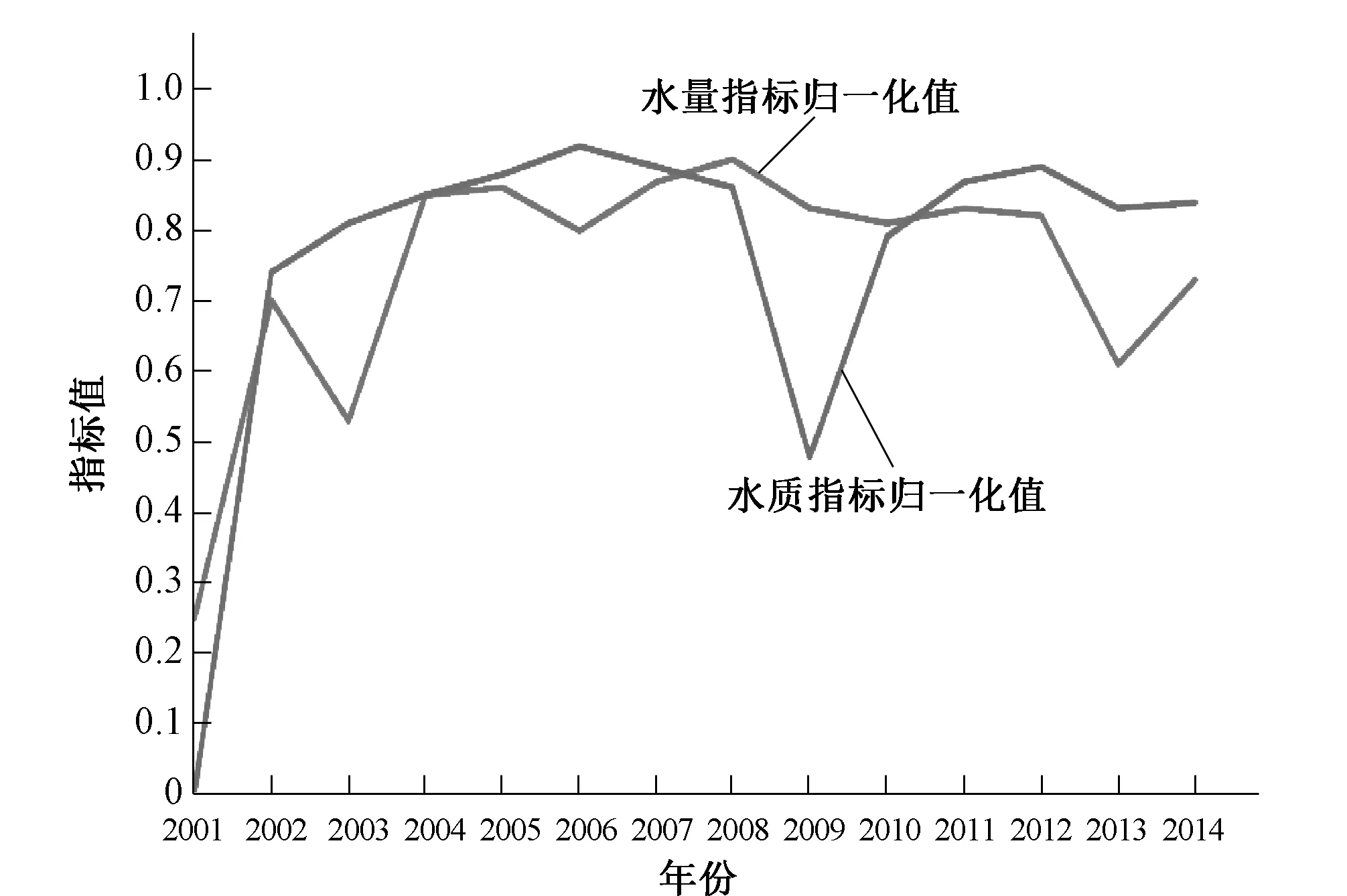
图4 北京市2001-2014年水量、水质指标归一化值Fig.4 Normalized Values of water quantity index and water quality index of Beijing between 2001 to 2014

将2001-2014年北京市水资源系统安全尖点突变模型的状态变量值和水量、水质指标归一化值代入式(13)，并利用Matlab中的regress函数求解得到系数矩阵B，得到拟合系数结果为k1=-1.64，k2=0.38，k3=0.16，R2为0.95，拟合效果良好，表明可以用此系数矩阵来表征状态变量与控制变量之间的关系。由u=k1u′，v=k2v′-k3, 可得北京市水资源安全尖点突变模型主次控制变量和突变判别式Δ的计算结果，同时与各年份的供需水量差值(需水量满足各部门用水需求)进行比较，结果见表4。

表4 北京市2001-2014年突变判别式值与水量供需差值对比Tab.4 Catastrophe indicator Δ and differences between watersupply and demand of Beijing from 2001 to 2014

图5 突变判别式Δ与水量供需差值关系拟合图Fig.5 Fitting graph of Catastrophe indicator Δ and difference between water supply and demand

根据表4绘制突变判别式Δ与水量供需差值的趋势线，采用多项式拟合，如图5。由图5得Δ与水量供需差值的拟合公式为Δ=2.779 4x2+32.263x+71.174，R2为0.86。由拟合公式可得当Δ=0时，水量供需差值为-2.96 亿m3，此时水资源系统安全状态处于临界点。

2.3 远景年份水资源安全情势评估

建立水资源安全突变模型的目的是寻求水资源安全状态变化的规律，防止水资源安全形势的破坏，保障区域社会经济发展，同时也能为远景年份的资源规划和管理提供依据。根据突变模型求得的水资源安全状态处于临界位置(Δ=0)时的水量供需差值，在对远景年份需水量合理预测的基础上，计算该年份安全供水的下限值，对该年的水资源安全情势进行评估，对区域水资源规划和可持续利用具有重要意义。

本文根据北京市2001-2014年需水量数据，采用灰色系统模型[14]，得出需水量预测模型为：Y(t)=84.739.69 e0.000 48(t-1)-84 697.55，由此预测2020年(t=20)和2030年(t=30)的需水量分别为：Y(20)-Y(19)=40.77 亿m3，Y(30)-Y(29)=40.96 亿m3。因此2020年、2030年北京市的安全供水下限值分别为：40.77-2.96=37.81 亿m3和40.96-2.96=38.00 亿m3。

查阅1988年至2014年北京市水资源公报得逐年供水量，通过频率计算，可得北京市供水保证率与供水量对应关系如图6，在50%、75%和90%的供水保证率下供水量分别为38.52、35.99和34.14 亿m3。在50%的供水保证率对应的供水量条件下，北京市2020年和2030年的安全供水需求均能得到满足，而在75%和90%的供水保证率对应的供水量下则会发生水资源安全破坏，75%的供水保证率下北京市2020年和2030年分别存在1.82和2.01 亿m3的供水缺口，90%的供水保证率下则分别存在3.67和3.86 亿m3的缺口，与《北京市“十二五”时期水资源保护及利用规划》[15]中的预测结果相近，表明本文建立的尖点突变模型和安全评价模型合理，计算结果可为北京市水资源可持续利用规划提供数据支撑。

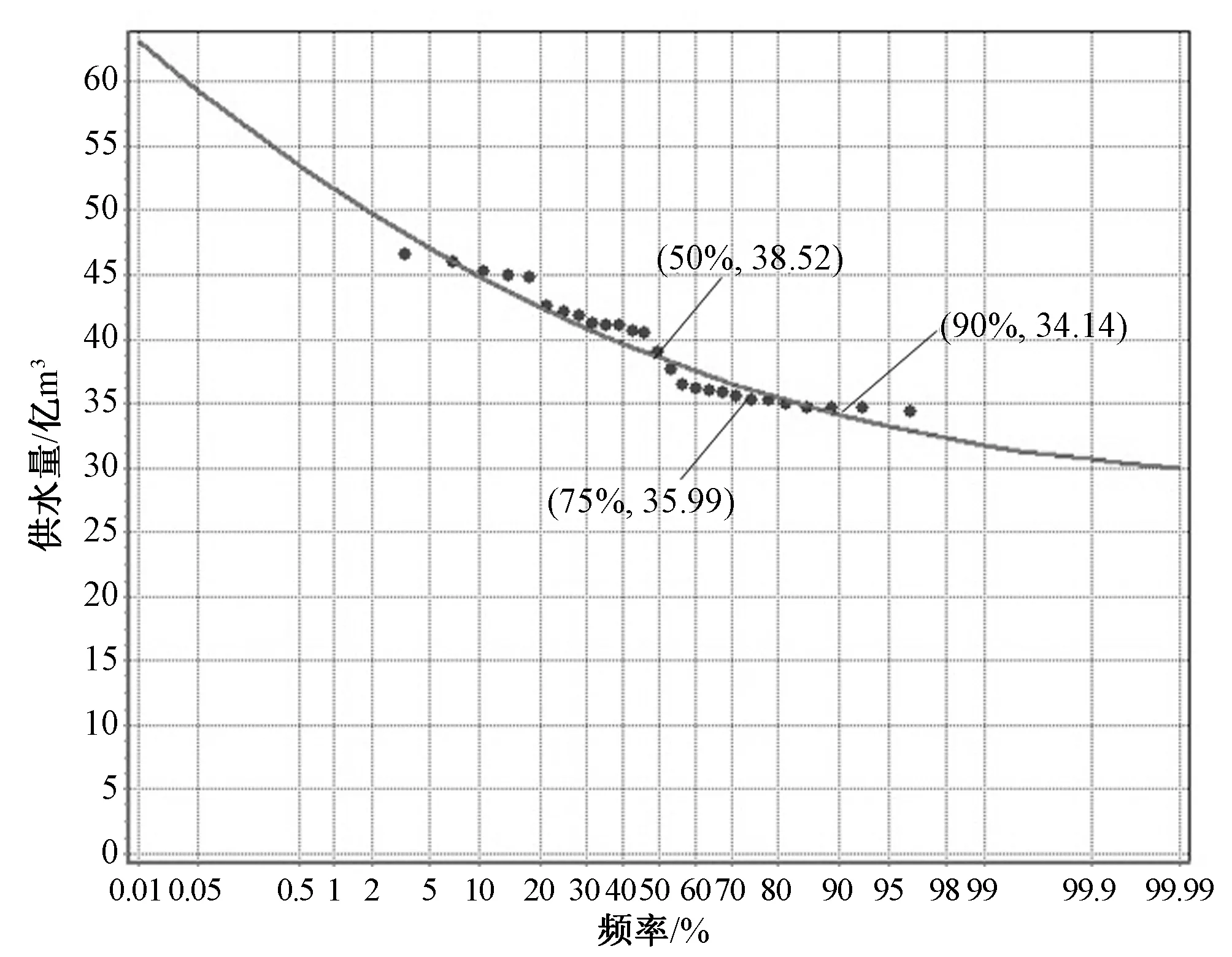
图6 北京市供水保证率曲线Fig.6 Water supply assurance rate curve of Beijing

3 结 语

(1)水资源安全研究聚焦水资源系统安全状况对区域社会经济发展的影响，通过探求水资源安全阈值，为区域水资源管理和规划提供重要依据，有助于促进水资源系统和社会经济的可持续发展，具有重要的理论和实践意义。

(2)水资源安全突变模型通过应用突变理论中的势函数，可建立表征水资源安全的状态变量与其影响因子即控制变量之间的关系。状态变量和控制变量的选取应综合考虑与水相关的自然环境、社会经济和生态安全等因素，从而在进行变量归一评价时根据指标的层次结构应用突变评价的方法。

(3)依据北京市水资源开发利用的现状，建立北京市水资源安全尖点突变模型，得出北京市水资源安全处于临界状态下的水量供需缺口为2.96 亿m3,并对远景年份2020和2030年的供水情势进行了评估，得出其安全供水下限分别为37.81和38.00 亿m3。

□

[1] 张玉山, 李继清, 梅艳艳,等. 基于突变理论的天津市水资源安全阈值分析模型[J]. 辽宁工程技术大学学报(自然科学版), 2013,(4):562-567.

[2] 郦建强, 王建生, 颜 勇. 我国水资源安全现状与主要存在问题分析[J]. 中国水利, 2011(23):42-51.

[3] Leeuwen C J V, Frijns J, Wezel A V, et al. City Blueprints: 24 Indicators to Assess the Sustainability of the Urban Water Cycle[J]. Water Resources Management, 2012,26(8):2 177-2 197.

[4] 贾绍凤, 张士锋. 海河流域水资源安全评价[J]. 地理科学进展, 2003,22(4):379-387.

[5] Schneider K, Turner J L, Jaffe A, et al. Choke point china: confronting water scarcity and energy demand in the world's largest country. [J]. Vermont Journal of Environmental Law, 2011.

[6] 高媛媛, 王红瑞, 许新宜,等. 水资源安全评价模型构建与应用----以福建省泉州市为例[J]. 自然资源学报, 2012,27(2):204-214.

[7] Lu S, Bao H, Pan H. Urban water security evaluation based on similarity measure model of Vague sets[J]. International Journal of Hydrogen Energy, 2016.

[8] 孙雪峰, 于 莲. 水生态系统的突变模型[J]. 水科学与工程技术, 2007,(1):39-41.

[9] 李继清, 张玉山, 纪昌明,等. 突变理论在长江流域洪灾综合风险社会评价中的应用[J]. 武汉大学学报(工学版), 2007,40(4):26-30.

[10] Chen Y, Zhang S, Zhang Y, et al. Comprehensive assessment and hierarchical management of the sustainable utilization of urban water resources based on catastrophe theory[J]. Journal of the Taiwan Institute of Chemical Engineers, 2016,60:430-437.

[11] Catastrophe Theory[M]. Springer Berlin Heidelberg, 1992,196.

[12] 王文俊, 张树深, 刘素玲,等. 基于突变理论的营口近岸海域环境灾害性风险分析[J]. 农业环境科学学报, 2010,29(s1):184-190.

[13] 汪党献, 王 浩, 马 静. 中国区域发展的水资源支撑能力[J]. 水利学报, 2000,(11):21-26.

[14] 程 辉, 尚琳琳, 牛彦涛,等. 基于灰色系统模型的北京市需水量预测分析[J]. 广东水利水电, 2013,(7):55-58.

[15] 北京市“十二五”时期水资源保护及利用规划[J]. 北京水务, 2012,(2):13-18,23.