基于正交试验设计的离心风机多因素优化研究

张 波，吕玉坤

1 前言

离心风机是火电厂的重要辅机，是仅次于泵的耗电大户［1］，其耗电量约占发电机组发电量的1.5%～3%，占厂用电的25%～30%［2］。因此，研究和改造风机，提高其性能，对火电厂的节能增效具有重要意义。

国内外对离心风机的研究多集中于叶轮和蜗壳结构，而对蜗壳型线的优化、叶轮与蜗壳之间轴向相对位置及径向相对位置的研究不多。黄东涛、张建、王建等对叶片通流部分进行了改造［3～5］。Dawes、Nursen、杨静等研究了蜗壳内部的三维旋转流动［6～8］。区颖达、吕玉坤等研究得出了合适的蜗舌间隙，可较好地降低泄漏损失和噪声［9，10］。宋宝军、程博利用数值模拟手段，分别对蜗壳宽度和蜗壳型线优化，提高了风机效率和全压［11,12］。郑金等提出多种节能改造方案，增压风机节电效果显著［13］。因此，耦合蜗壳宽度、蜗舌间隙及叶轮轴向相对位置三因素，探寻最优耦合方案，就有可能提高风机性能。

本文以G4-73№8D型离心风机为研究对象，在蜗壳型线优化的基础上，采用正交试验设计方法耦合蜗壳宽度、蜗舌间隙及叶轮轴向相对位置三因素［14］，利用Fluent数值模拟软件，对耦合风机的内部三维流场进行数值模拟，研究其蜗壳内部流动特性，以提高风机性能。

2 正交试验

正交试验设计是利用正交性原理编制并已标准化的正交表，科学安排试验方案，得到的试验结果再用数理统计方法进行处理，使之得出科学结论。

2.1 试验目的

探索基于蜗壳型线优化，耦合蜗壳宽度A、蜗舌间隙B、叶轮轴向相对位置C（叶轮后盘与蜗壳后端的间距）三因素后，离心风机全压与效率都提升的方案。

2.2 试验因素与试验方案

本文试验因素为蜗壳宽度A、蜗舌间隙B、叶轮轴向相对位置C，通过文献可知因素水平。选择因素水平如表1所示。选用正L9（34）交表，确定试验方案如表2所示。正交表安排试验，理论试验方案 9 组：A1B1C3、A2B1C1、A3B1C2、A1B2C2、A2B2C3、A3B2C1、A1B3C1、A2B3C2、A3B3C3；由于计算周期及模型建立耗时较长，本文实际选取G4-73原风机、A1B3C1（型线优化风机）、A3B3C3（耦合风机）3组试验方案。

表1 因素水平

表2 试验方案

3 几何结构的对比和数值方法

3.1 原风机和蜗壳型线优化风机几何结构对比

蜗壳型线优化风机减小了小旋转角处的蜗壳型线半径，增加了大旋转角处的蜗壳型线半径，其与原风机几何结构对比，如图1所示。

图1 原风机与蜗壳型线优化风机几何结构

3.2 原风机和蜗壳宽度优化风机几何结构对比

根据文献［11］计算得到，当G4-73№8D型离心风机叶轮前盘与蜗壳前端面间的距离减小20mm，叶轮后盘与蜗壳后端面间的距离增加40mm时，与原风机相比，风机效率和全压得到较大幅度提高，其与原风机几何结构对比，如图2所示。

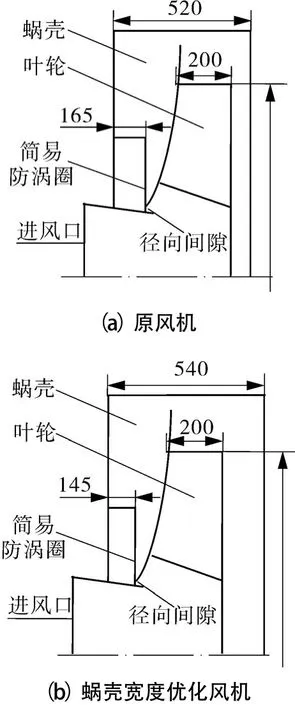
图2 原风机与蜗壳宽度优化风机几何结构

3.3 数值方法

3.3.1 网格划分

本文将风机模型分为集流器、叶轮、蜗壳及进口延长段4个流动区域，对风机叶轮和风机蜗壳采用非结构网格，而集流器和进口延长段采用结构网格。经网格无关性验证，风机的网格总数约为220万个，如图3所示。

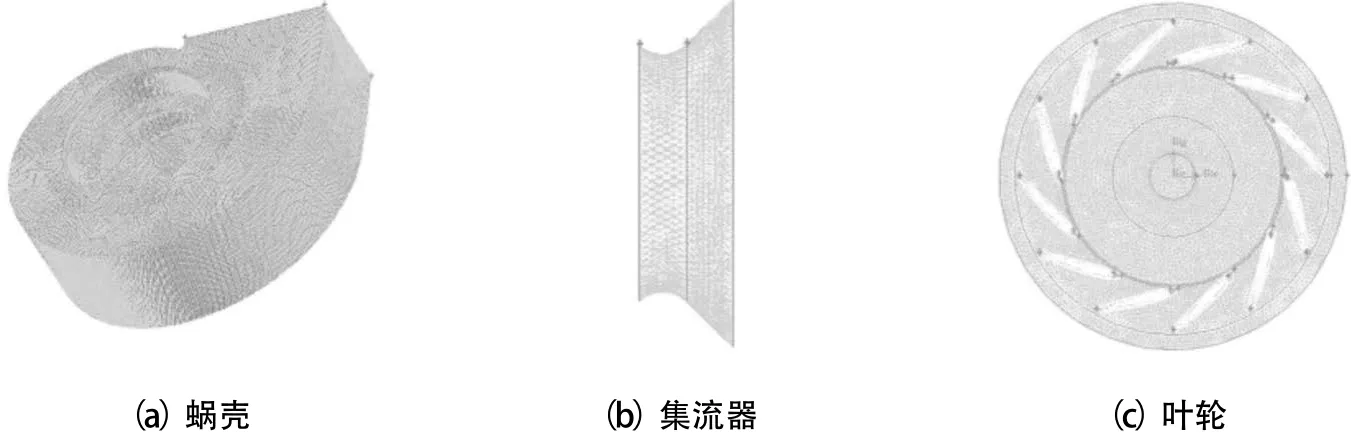
图3 风机网格示意

3.3.2 边界条件设置

（1）进口边界条件：以进口延长段进口作为速度进口，进气方向为轴向，速度大小是18 m/s，温度是293 K。

（2）出口边界条件：蜗壳出口设置为压力出口，出口静压为1.675kPa。

（3）壁面边界条件：风机模型包含旋转的动边界和静止的静边界，将整个计算域划分成定子和转子2个子区域［15～20］。旋转叶轮和静止蜗壳之间的耦合采用多参考坐标系模型（简称MRF）。先设置转子和静子的交界面，然后设置对应实体的转速，旋转壁转速为1450 r/min非旋转壁面为0。

4 计算结果分析

4.1 蜗壳型线优化风机与原风机结果分析

以风机的全压和效率作为衡量改造方案优劣的指标。当风机处于额定转速（1450 r/min），分别对蜗壳型线优化和原风机在负荷为65%、75%、82%、86%、100%、105%和110%5个工况下进行数值计算，并对改造风机的全压和效率与原风机的全压和效率进行比较，如图4，5所示。

图4 型线优化风机与原风机的全压对比

图5 型线优化风机与原风机的效率对比

表3为型线优化风机相对于原风机在风机负荷为65%～110%内的全压和效率的平均增长值。

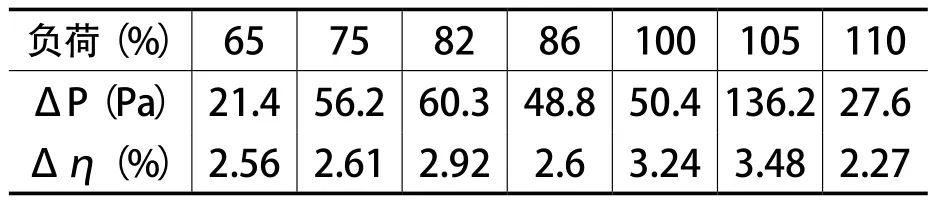
表3 全压和效率的平均增长值

从图4、5和表3可以看出：在负荷为65%、75%、82%、86%、100%、105%和110%的7个工况下，型线优化后风机的全压和效率较原风机都提高了；从总体上，型线优化风机与原风机比较，全压平均提高57.3 Pa，相对提高了3.64%，效率平均提高了2.81%。

4.2 耦合风机与原风机结果分析

当风机处于额定转速（1450 r/min），分别对原风机和耦合风机在风机负荷为65%、75%、82%、86%、100%、105%和110%的7个工况下进行数值计算，并对耦合风机的效率和全压与原风机的效率与全压进行比较，结果如图6，7所示。表4为耦合风机相对于原风机在风机负荷为65%～110%内的效率和全压的平均增长值。从图6，7和表4可以看出：在负荷为65%、75%、82%、86%、100%、105%和110%的7个工况中，65%负荷的工况下，耦合风机较原风机，全压和效率略微下降，其它负荷下耦合风机的全压和效率都提高了；从总体上，耦合风机与原风机比较，全压平均提高32.5 Pa，相对提高了2.07%，效率平均提高了1.36%。

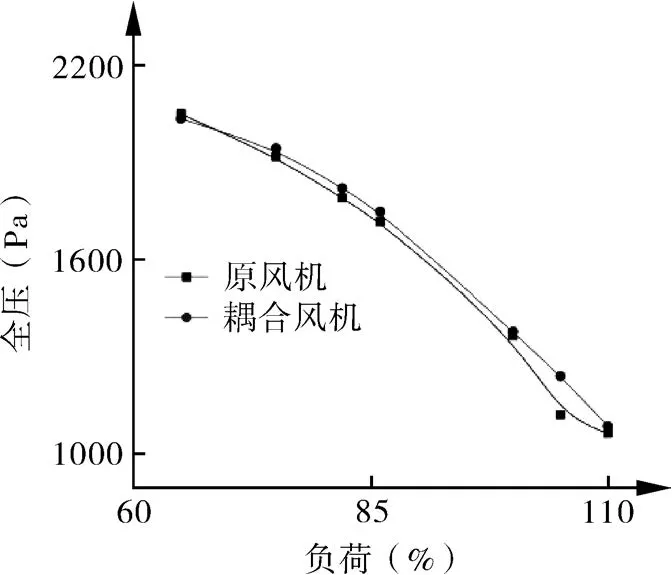
图6 耦合风机和原风机的全压对比

图7 耦合风机与原风机的效率对比

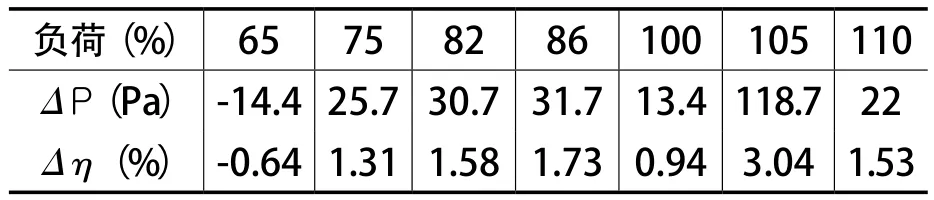
表4 全压和效率的平均增长值

4.3 耦合风机内流场分析

图8为原风机、型线优化风机和耦合风机的全压对比云图。

图8 3种风机全压云图

从图上可以看出，型线优化风机和耦合风机蜗壳区域内全压得到很大提高，主要是由于型线优化风机和耦合风机都减小了蜗舌间隙，增加了蜗壳的扩压区域，从而提高了风机全压

图9所示为原风机、型线优化风机和耦合风机的静压对比云图，从图上可以看出，在叶轮内，静压沿半径方向是逐渐增大的；在蜗壳通道中，静压随蜗壳半径的增大亦增大，这表明速度在迅速减小，动能转化为压力能。在原风机的L处，存在压力较低的区域，其形成是因为从叶轮出来的高速气流没有蜗壳环壁阻挡，不能马上减速扩压，而是通过一个缓慢过程减速升压，从而该处压力相对较低；另外，由于蜗壳出口通流截面积较小，导致速度增加，从而降低了静压。原设计蜗壳通流面积较窄小，而优化后风机蜗壳通流面积变宽，气流在蜗壳通道出口处加速不明显，低压区L也就缩小了。

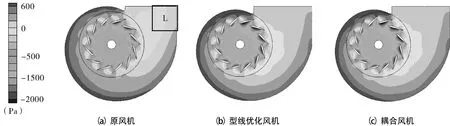
图9 3种风机静压云图

图10所示为原风机、型线优化风机和耦合风机的速度对比云图，从图上可以看出原风机在蜗壳出口处流场较为混乱，低压区域处的速度较高，此处部分压能转化为动能。比较型线优化风机和耦合风机，风机出口速度场分布均匀。

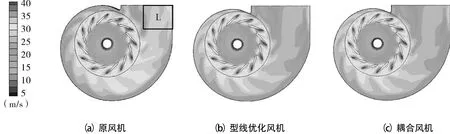
图10 3种风机速度云图

4.4 性能曲线分析

由图11可看出，当相对流量在27%～110%之间时，优化风机的全压整体高于原风机。在相对流量为27%～65%时，耦合风机全压高于型线优化风机；当相对流量大于65%时，型线优化风机全压高于耦合风机，较原风机提高3.61%，较耦合风机提高1.54%。

图11 3种风机全压曲线

由图12可看出，当相对流量在27%～110%之间时，优化风机的静压亦整体高于原风机。在相对流量为27%～65%时，耦合风机静压高于型线优化风机；当相对流量大于65%时，耦合风机静压和型线优化风机静压相差不大。

图12 3种风机静压曲线

由图13可以看出，对风机进行型线优化和耦合优化改造，在相对流量处于30%～110%之间时，两种优化蜗壳后的风机，效率较原风机整体提高。当相对流量为22%～40%时，耦合风机的效率高于型线优化风机。

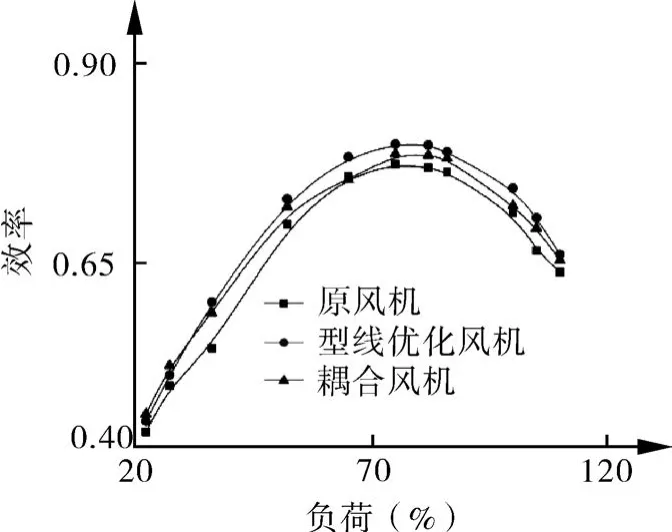
图13 3种风机效率曲线

综合图11～13，在小流量工况下，耦合风机的全压、静压、效率高于原风机和蜗壳型线优化风机，因而，变工况能力更强；当相对流量处在40%～110%之间时，耦合风机与型线优化风机较原风机，全压、静压、效率都提高，型线优化风机提高的更多，因而，此段负荷区间，蜗壳型线优化风机变工况能力更强。

图14为3种风机轴功率曲线。由图14可以看出，随着流量的增大，两种风机的轴功率也随之增大，且优化风机功率均小于原风机；相对流量处在22%～30%时，耦合风机轴功率小于型线优化风机；当相对流量处于30%～110%时，型线优化风机轴功率小于耦合风机。从风机运行耗电量来考虑，小流量运行时，耦合风机较为节能；而在大流量运行时，型线优化风机相对节能。

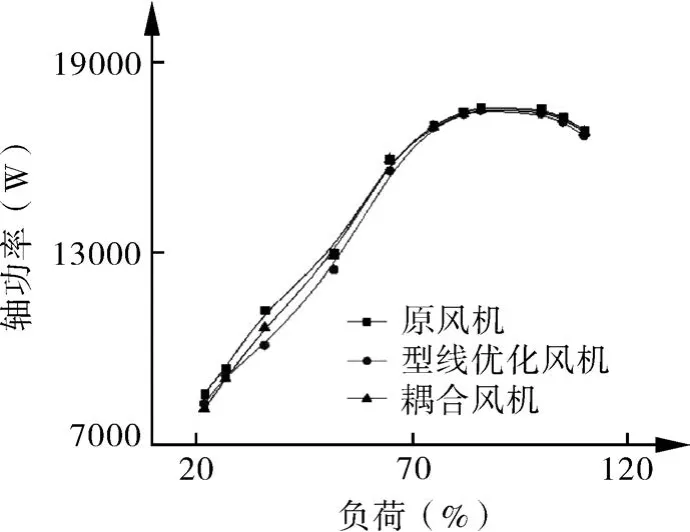
图14 3种风机轴功率曲线

5 结论

（1）正交试验设计方法耦合蜗壳宽度、蜗舌间隙及叶轮轴向相对位置三因素，为离心风机优化研究提供借鉴意义。

（2）当风机负荷处于65%～110%之间，型线优化后风机的全压和效率较原风机都提高了，全压平均提高57.3Pa，相对提高3.64%，效率平均提高2.81%；耦合风机在65%负荷的工况下，较原风机，全压和效率略微下降，其它负荷下耦合风机的全压和效率较原风机都提高了，全压平均提高32.5Pa，相对提高2.07%，效率平均提高1.36%。

（3）在小流量工况下，耦合风机变工况能力更强，其它工况下，型线优化风机变工况能力较强。从风机运行耗电量来考虑，小流量运行时，耦合风机较为节能；而在大流量运行时，型线优化风机相对节能。

［1］ 吕玉坤，葛则锟，李春曦.基于折算转速的离心泵并联节流调节经济性分析［J］.试验室研究与探索，2012,31（2）：33-35.

［2］ 王松岭，骞宏伟，李春曦，等.基于最小二乘法的离心风机叶轮参数优化研究［J］.热力发电，2009，38（12）：24-28.

［3］ 黄东涛，边晓东，唐旭东,等.长短叶片开缝技术在离心风机设计中的应用［J］.清华大学学报（自然科学版），1999，39（4）：6-9.

［4］ 张建.G4-73№8D风机叶轮改造数值模拟与试验研究［D］.保定：华北电力大学，2006.

［5］ 王建.离心风机叶轮附加小叶片长度的优化研究［D］.保定：华北电力大学，2006.

［6］ Dawes WN.A simulation of the unsteady interaction of a centrifugal impeller with its vaned diffuser：flow analysis［J］.Journal of Turbomachinery.1995；117:213-22.

［7］ NursenEC,Ayder E.Numerical calculation of the three-dimensional swirling flow inside the centrifugal pump volutes［J］.International Journal of Rotating Machinery.2003（9）:247-253.

［8］ 杨静.叶轮机械轴向蜗壳内部流动的数值分析［D］.武汉：华中科技大学，2005.

［9］ 区颖达，游 斌. 分体空调室内体贯流风机蜗舌间隙对气动特性的影响［J］.风机技术，2001（4）:8-11.

［10］ 吕玉坤，张波，程博.基于CFD的离心风机叶轮中心位置优化研究［J］.风机技术，2015（4）:38-43.

［11］ 宋宝军. 基于CFD的离心风机蜗壳与叶轮相对位置优化研究［D］.保定：华北电力大学，2013.

［12］ 程博.G4-73离心风机叶轮与蜗壳径向适配性研究［D］.保定：华北电力大学，2014.

［13］ 郑金，何建业，周欣安.330MW机组脱硫增压风机节能改造［J］.热力发电，2011,40（3）：69-71.

［14］ 董如何，肖必华，方永水.正交试验设计的理论分析方法及应用［J］.安徽建筑工业学院学报（自然科学版），2004（6）:103-106.

［15］ 陈阳，黄友根，王军，等.倾斜蜗舌对前弯离心风机蜗舌区域流动影响的数值研究［J］.流体机械，2015，43（9）：26-30.

［16］ 常超，何奕为，吴俊锋，等.双进气后向离心机的气动性能数值模拟及其改进［J］.流体机械，2016，43（6）：44-46.

［17］ 贾志彬，陈强，汪军，等.微穿孔消声器在小型高速离风机中的应用研究［J］.流体机械，2015，43（8）：6-10.

［18］ 韩平，王天堃，孟永毅.基于LS-SVM的一次风机振动在线监测及故障预警研究［J］.机电工程，2016，33（5）：629-632.

［19］ 王小华，任轶，戴侃，等.高速泵效率影响因素的正交试验研究［J］.化工设备与管道，2016，53（2）：43-46.

［20］ 游斌，Elhadi E E，谢军龙，等.多翼离心风机的三维数值模拟［J］.工程热物理学报,2003,24（3）：439-422.