浙江近海热带气旋极值风速统计及重现期分析

刘甜甜,汪一航,2*,裴军峰,梅秋莹

(1.宁波大学理学院,浙江宁波315211;2.宁波非线性海洋和大气灾害系统协同创新中心,浙江宁波315211) 3.国家海洋局东海信息中心,上海200136)

浙江近海热带气旋极值风速统计及重现期分析

刘甜甜1,汪一航1,2*,裴军峰3,梅秋莹1

(1.宁波大学理学院,浙江宁波315211;2.宁波非线性海洋和大气灾害系统协同创新中心,浙江宁波315211) 3.国家海洋局东海信息中心,上海200136)

极值风速重现期不仅是海岸工程设计的重要参考项,也是海洋预报部门发布预报、预警的重要依据。因此,本文通过统计分析1949-2015年之间经过浙江近海的热带气旋过程中的风速极值,采用P-III分布和Gumbel分布求矩适线法对其进行重现期的计算。由最小二乘法准则可知,P-III分布求矩适线法的拟合曲线优于Gumbel分布求矩适线法的拟合曲线,能够很好地拟合实测数据序列。比较P-III分布和Gumbel分布的计算结果可知, P-III分布计算结果更符合实测数据,且其计算的百年一遇极值风速设计值为92.26 m/s。此外,文中还对计算方法进行了Matlab编程设计,以自适应的过程选取与数据序列拟合最好的曲线,不仅在计算方法上,而且在操作方式上,都较传统适线法更具有客观性和有效性。

极值风速;P-III分布;Gumbel分布;重现期

极值风速重现期作为海岸工程设计的重要参考项,也是政府及海洋预报部门发布预警、预报的重要依据,其在海洋防灾减灾中具有重要意义[1]。而海岸工程设计中,极值风速重现期的计算普遍采用P-III分布和Gumbel分布(也称极值Ⅰ型分布)。

目前,P-III分布常用的估计方法有线性矩法、概率权重矩法、极大似然法和优化适线法:其中,线性矩法是概率权重矩的线性组合,是在传统矩法基础上做的改进,其计算结果都只能作为估计的初值[2-3];极大似然法在理论上是无偏和有效的,但因其似然方程在Cs≥2时无解,故很少使用[4-5];优化适线法是在一定的准则下,选出与经验点据拟合最好的频率曲线参数的方法,是一种较好的估计方法[3,5]。Gumbel分布常用的参数估计方法有矩法、概率加权矩法、极大似然法和适线法(包含Gumbel):黄浩辉等[6]认为Gumbel法在大多数情况下对广东省风速序列的拟合效果最好。

国内对极值风速重现期计算的研究有:陈朝晖等[7]通过3种分布函数包含极值Ⅰ型、II型、反向Weibull分布,对厦门地区年最大风速进行不同重现期的计算;金连根[8]以台湾岛花莲港海域热带气旋资料为例,采用Poisson-P-III分布计算了设计风速;李运斌[9]采用Poisson-Weibull复合极值分布对湛江近海36 a的风速极值进行了多年一遇设计风速的计算。

基于上述分析,本文通过搜集1949-2015年之间所有经过浙江近海的共99个热带气旋过程中的风速极值,采用矩法初估P-III分布和Gumbel分布的参数,然后以最小二乘法准则来选配拟合最好的曲线,并对拟合结果进行了K-S检验,以期为海洋防灾减灾中的相关工作提供参考。

(王佳实 编辑)

由于MATLAB软件具有可读性和简便性,其得到了越来越多学者的认可:李清富等[10],张炳蔚等[11]实现了P-III分布在MATLAB平台上的计算,尚英姿和安润秋[12]基于MATLAB计算了Gumbel分布。基于前人的研究,本文的所有计算都在MATLAB软件平台上编程实现。

1 分布函数

1.1 P-III分布

Pearson III型分布(P-III分布),数学上常称伽玛分布,对陆机变量(x),其概率密度函数为

式中,形状参数α、尺度参数β和位置参数a0分别由下式计算:

对密度函数进行积分,可以得到等于及大于一定数值xp的累积频率P值,即

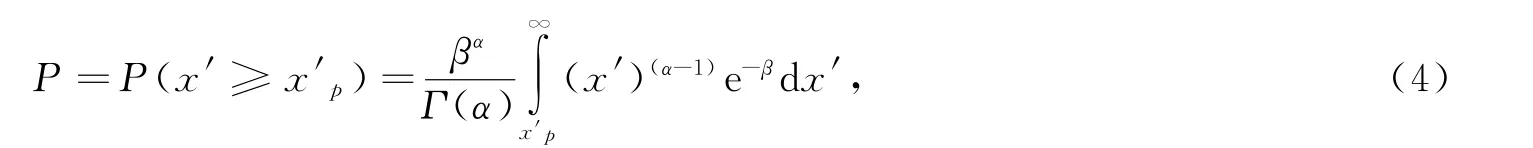
则上式中x'服从参数为(α,1/β)的伽玛分布,且xp=x'p+a0。

1.2 Gumbel分布

Gumbel分布,也称极值Ⅰ型分布,分布函数为

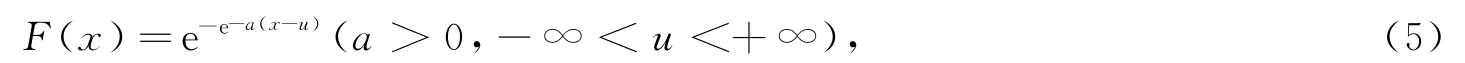
式中,a为尺度参数;u为位置参数[13]。

当重现期为T时,极值风速设计值为

令x'=x-a0,则x=x'+a0,上述积分式变为

2 参数估计

2.1 P-III分布求矩适线法

2.1.1 求 矩

2.1.2 计算经验频率

把实测数据按从大到小的顺序排列,得到序列{x1,x2,…,xm,…,xn},序列中某一变量大于等于xm的可能性即为频率,一般用符号Pm来表示,计算公式为

2.1.3 适线准则

最小二乘法准则又称离差平方和最小准则(即OLS准则),是通过样本数据与由拟合分布计算出的对应频率处设计值之间的差的平方和,来反映样本数据与拟合曲线的偏离程度的一种方法。与另外两种准则:离差绝对值和准则、相对离差平方和准则相比,其得到的频率曲线与点据拟合最好,且对大数据反应灵敏[14],其目标函数为

式中,xPm为第m项的累积频率Pm对应计算出来的极值风速设计值;xm为第m项样本值。

2.2 Gumbel分布求矩适线法

求矩适线法,即用求矩公式计算出均值和均方差,然后用OLS准则(最小二乘法准则)拟合曲线,估计参数。

2.2.1 求 矩

一阶矩即数学期望E(x)、二阶矩即均方差σ的计算公式为

2.2.2 适线准则

根据经验频率公式(9),计算如下序列:

3 估计方法实现

P-III分布的参数求解,在Matlab中实现的具体步骤如下:

1)用xlsread函数导入实测数据,并用mean函数算出。由式(7)算出,Cv,Cs,再由式(8)算出其均方误差σ,σCv,σCs,进而求出其相对误差sσ,sσCv,sσCs;

2)第1层循环,Cv在[Cv(1-sσCv),Cv(1+sσCv)]内以一定的步长(如0.01,0.1等;步长越小,计算结果越精确,但相应的循环次数越多,程序运行时间越长)变化;第2层循环,Cs在[Cs(1-sσCs),Cs(1+sσCs)]内以一定的步长变化,这时对于每一个Cs,都可以算出一组对应的(α,β,a0);

3)对于每一组(α,β,a0),都对应一个P-III分布,可用Matlab中伽玛函数的逆函数ga min v (Pr obability,α,β)来求解,对于经验频率Pm,其对应的设计值为xPm=ga min v(1-Pm,α,1/β)+a0。按照OLS准则,计算出xPm与样本值x之间的离差平方和Δ=sum(xPm-x)2;

4)选择出最小的Δ,并记录对应的(α,β,a0),然后计算出Cv,Cs,绘出P-III曲线,并由x1/T=ga min v(1 -1/T,α,1/β)+a0计算出T年一遇的极值风速。

4 K-S检验

Kolmogorov-Smirnov检验(K-S检验)是通过比较样本数据的累积频率分布P(x)与特定理论分布G(x)的差距来推论该样本是否取自某一特定分布族的检验方法[15]。其原假设H0:样本来自的总体分布服从某一特定分布。设D为P(x)与G(x)差距的最大值,则有

当实际观测的D＜D(n,α)时(其中n为样本数,α为信度),接受H0假设,否则不接受H0[15]。

在Matlab中用[h,p,k,c]=kstest(X,cdf,alpha)函数来检验样本数据X是否服从累积分布函数为cdf的分布。式中,cdf为指定累积分布函数;alpha为指定测试水平;h值为0表示接受原假设,值为1表示不接受原假设;p为原假设成立的概率;k为测试统计量的值,小于c时接受原假设;c为是否接受原假设的临界值。

5 实例计算与分析

5.1 资料搜集与整理

搜集1949-2015年期间内所有经过浙江近海(120°6'～123°6'E,27°～31°N)区域的热带气旋资料,并整理热带气旋过程期间的最大风速值,共得到99个热带气旋的风速极值。其中,1949-1980年的数据来源于上海热带气旋研究所编写的《西北太平洋台风基本资料集》[16];1981-1988年的热带气旋数据来源于《台风年鉴》[17],1989-2014年的热带气旋数据来源于《热带气旋年鉴》[18],还参考了一些学者文章中的数据和资料[19-22]。

对搜集整理完成的热带气旋极值风速资料进行分析,可得:统计资料中,属于热带风暴(极值风速在17.2～24.4 m/s)的共有4个;属于强热带风暴(极值风速在24.5～32.6 m/s)的有16个;属于台风(极值风速在32.7～41.4 m/s)的有24个;属于强台风(极值风速在41.5～50.9 m/s)的有16个;属于超强台风的(极值风速大于等于51 m/s)有39个。以上统计中,台风、强台风和超强台风一共有79个,表明经过统计区域的台风中12级及以上强度的热带气旋居多。

所统计资料中,极值风速在80 m/s以上的有5822号、5612号和5310号台风,其过程中的最大风速分别为84,82和82 m/s,且在浙江附近的路径图如图2所示。

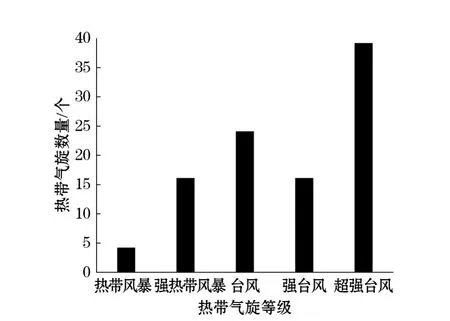
图1 1949-2015年热带气旋类型分布图Fig.1 Numbers of different types of tropical cyclones during 1949-2015

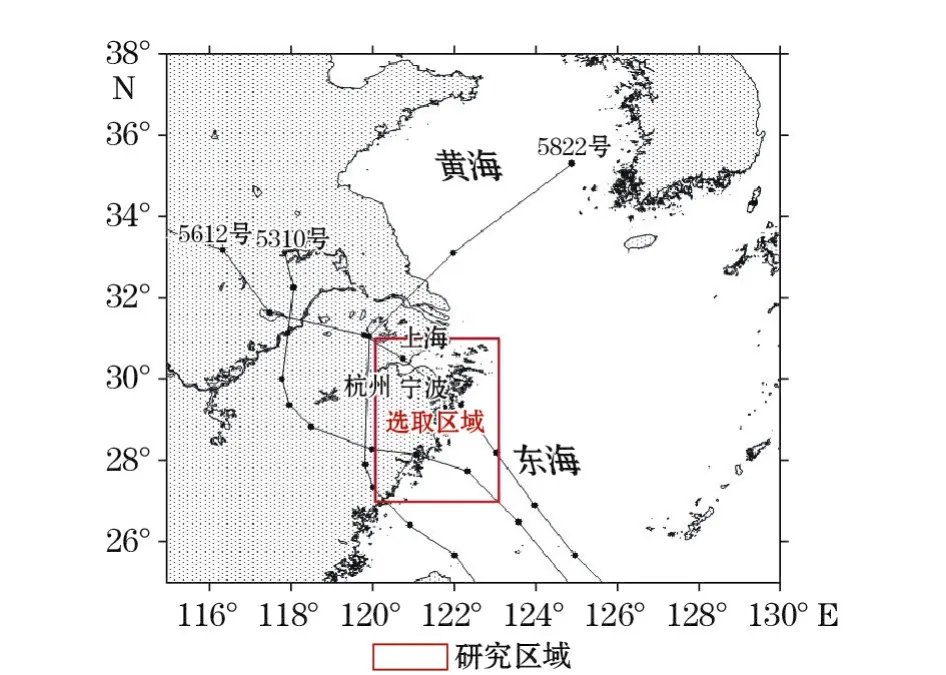
图2 3个最大极值风速热带气旋路径图Fig.2 Paths of the three tropical cyclones with extreme wind speed greater than 80 m/s

5.2 计算结果分析

用P-III分布求矩适线法对极值风速序列进行拟合,结果如图3所示,得到相关计算结果如表1和表2所示。

图3 P-III分布拟合曲线示意图Fig.3 Fitting curve of P-III distribution of extreme wind speed

由图3可知,实测数据点能够均匀的分布在拟合曲线两边,表示曲线与实测数据的拟合效果较好。

表1 矩法计算参数的结果和相对误差Table 1 Coefficients and relative errors based on moments method

表2 P-III分布拟合结果Table 2 Results based on fitting curve of P-III distribution

由表2可知,P-III分布求矩适线法拟合结果的K-S检验k,c值分别为0.08和0.13,在K-S检验的Matlab计算结果中,c表示接受原假设的临界值,k表示测试统计量的值,当k小于c时,表示接受原假设,即样本来自的总体分布服从拟合得到的分布;用P-III分布求矩适线法拟合的曲线与实测数据点的离差平方和为384.93,计算得到的100 a一遇的极值风速设计值为92.26 m/s;调整之后的,Cv,Cs)值为(47.28,0.35, 0.52),其中值未做调整,Cv值调整了2%,Cs值调整了约44%。另外,由表2中的计算结果可知,统计资料中出现的最大极值风速84 m/s的重现期约为50 a一遇。

其次,用Gumbel分布求矩适线法对极值风速序列进行拟合分析,结果如图4所示,相关计算结果如表3所示。

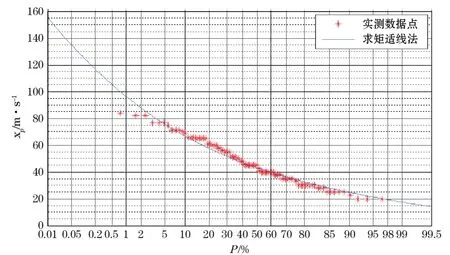
图4 Gumbel分布拟合曲线示意图Fig.4 Fitting curve of Gumbel distribution of extreme wind speed

由图4可知,横坐标P值在10%～40%之间的实测数据点都在拟合曲线的上侧,而在70%～95%的实测数据点都在拟合曲线的下侧,未均匀的分布在曲线两侧,故Gumbel分布求矩适线法与实测数据的拟合结果稍差。

表3 Gumbel分布拟合结果Table 3 Results based on fitting curve of Gumbel distribution

由表3可知,Gumbel分布求矩适线法拟合结果的K-S检验k,c值分别为0.08和0.13,k值小于C值,表示接受原假设,即样本来自的总体分布服从拟合得到的分布;用Gumbel分布求矩适线法拟合的曲线与实测数据点的离差平方和为854.50;计算得到的100 a一遇的极值风速设计值为100.1 m/s。

表4 P-III分布和Gumbel分布适线法拟合结果Table 4 Fitting results of P-III distribution and Gumbel distribution with moments method

表4是P-III分布和Gumbel分布求矩适线法的拟合结果对比,从表中可知,P-III分布的离差平方和384.93明显小于Gumbel分布的离差平方和854.50,表示实测数据点与P-III分布求矩适线法拟合曲线的偏离程度明显小于Gumbel分布拟合曲线与实测数据的偏离程度。

由表4可知,Gumbel分布的计算结果都大于P-III分布的计算结果;且随着重现期的增加,相对偏差也增大,整体相对偏差介于0.06%到11.13%之间。Gumbel分布求矩适线法计算的50 a一遇的极值风速为90.97 m/s,100 a一遇的极值风速为100.10 m/s;P-III分布求矩适线法计算的50 a一遇的极值风速为85.95 m/s,100 a一遇的极值风速为92.26 m/s。但由统计资料可知,67 a间经过统计区域的99个热带气旋中,极值风速的最大值为84 m/s。因此,P-III分布的计算结果(50 a一遇的极值风速为85.95 m/s)与实际统计资料(67 a间最大极值风速84 m/s)较接近。

6 结 论

本文通过搜集1949-2015年经过浙江近海区域的热带气旋的极值风速,采用P-III分布和Gumbel分布求矩适线法拟合实测序列,并计算极值风速重现期,以期为海岸工程规划和风速预报、预警等海洋防灾减灾相关工作提供参考。所有方法均采用Matlab编程实现,并给出了算法设计。主要内容及结果如下:

1)对P-III分布和Gumbel分布用求矩适线法计算经过浙江近海统计区域的极值风速重现期,可得: P-III分布和Gumbel分布的拟合结果均通过了K-S检验,表示样本来自的总体分布服从拟合得到的分布;但P-III分布与实测序列的离差平方和384.93明显小于Gumbel分布与实测数据的离差平方和854.50,表示PIII分布求矩适线法与统计的极值风速序列拟合较好。用P-III分布求矩适线法计算的100 a一遇的极值风速设计值为92.26m/s。

2)P-III分布与实测序列的离差平方和384.93明显小于Gumbel分布与实测数据的离差平方和854.50,表示P-III分布求矩适线法与统计的极值风速序列拟合较好,由P-III分布计算结果可知,50 a一遇的极值风速设计值为85.95 m/s;由Gumbel分布的计算结果可知,50 a一遇的极值风速设计值为90.97 m/s。但统计的67 a间共99个热带气旋中,只有1个台风的风速极值达到了84 m/s,有2个达到了82 m/s。所以,P-III分布求矩适线法的拟合结果更符合实际观测数据。

3)目前工程计算中经常采用的传统适线法是通过矩法计算参数,Cv,Cs)的值,作为初值,然后由操作人员对Cs/Cv的比值进行调整,以选配对数据序列拟合最好的曲线,其拟合结果会在一定程度上依赖于操作人员的经验,人为主观因素影响较大。文中给出的P-III分布和Gumbel分布下的求矩适线法,采用搜索算法,由适线准则来选配对数据序列拟合较好的曲线,这种自适应的过程,能够很大程度的避免操作人员的主观性,同时还能规避数据本身的局限性带来的缺陷。但文中的研究问题是对未来情况的预测,对其结果的合理性检验,除了从计算方法和数据规律为出发点,还需要更多、更长的历史观测数据和实际应用的检验。

[1] MA Y,ZHANG Q H.Approaches to several problems about progress in the study of typhoon[J].Journal of Oceanography of Huanghai& Bohai Seas,1999,17(1):61-65.马艳,张庆华.关于台风风场研究进展的若干问题探讨[J].黄渤海海洋,1999,17(1):61-65.

[2] LI T X,SONG M B.Comparative analysis of parameter estimating methods of Pearson Type-III distribution[J].Journal of Changjiang Engineering Vocational College,2008,25(3):44-47.李太星,宋萌勃.皮尔逊III型分布参数估计方法的对比分析[J].长江工程职业技术学院学报,2008,25(3):44-47.

[3] JIN G Y.Rationality analysis of the results from hydrologic frequency computation[J].Journal of China Hydrology,2009,29(2):10-14.金光炎.水文频率计算成果的合理性分析[J].水文,2009,29(2):10-14.

[4] YU Y Y,HE X.Maximum likelihood estimation of P-III curve and its application[J].Yangtze River,2012,42(21):21-23.余泱悦,贺信.PIII型曲线的极大似然估计及应用[J].人民长江,2012,42(21):21-23.

[5] CONG S Z,TAN W Y,HUANG S X,et al.Statistical testing research on the methods of parameter estimation in hydrological computation [J].Journal of Hydraulic Engineering,1980,(3):1-15.丛树铮,谭维炎,黄守信,等.水文频率计算中参数估计方法的统计试验研究[J].水利学报,1980,(3):1-15.

[6] HUANG H H,SONG L L,ZHI S Q,et al.Comparison of estimation of wind speed extreme-Ⅰdistribution parameters in Guangdong province[J].Meteorological Monthly,2007,33(3):101-106.黄浩辉,宋丽莉,植石群,等.广东省风速极值Ⅰ型分布参数估计方法的比较[J].气象,2007,33(3):101-106.

[7] CHEN C H,TANG H T.Distribution models of extreme typhoon winds based on numerical simulation of wind data[J].Journal of Chongqing University,2008,31(11):1285-1289.陈朝晖,汤海涛.台风极值风速的数值模拟及分布模型[J].重庆大学学报,2008,31(11): 1285-1289.

[8] JIN L G.Compound extreme value distribution and its application in calculation of design wind velocity in typhoon areas[J].Journal of Water Resources and Architectural Engineering,2014,12(3):138-168.金连根.复合极值分布及其在台风多发海域设计风速推算中的应用[J].水利与建筑工程学报,2014,12(3):138-168.

[9] LI Y B.Compound extreme value analysis of typhoon wind speed of Zhanjiang coastal waters[J].Journal of Meteorological Research and Application,2010,31(S2):111-113.李运斌.湛江近海台风风速复合极值分析[J].气象研究与应用,2010,31(S2):111-113.

[10] LI Q F,YAN P F,SUN J T,et al.Development of Matlab program for hydrological frequency curve drawing[J].Henan Science,2013,31 (8):1250-1254.李清富,闫鹏飞,孙静涛,等.水文频率曲线绘制的Matlab程序设计[J].河南科学,2013,31(8):1250-1254.

[11] ZHANG B W,HE W L,ZHOU C.Realization of matrix curve-fitting method in P-III distribution based on MATLAB and estimation of Beihai hydrological station's design wave height[J].Journal of Water Resources and Architectural Engineering,2013,11(5):27-31.张炳蔚,何文亮,周冲.P-III分布求矩适线法MATLAB实现与北海海域设计波高估计[J].水利与建筑工程学报,2013,11(5):27-31.

[12] SHANG Y Z,AN R Q.Maximum likelihood estimation of the parameters of the extreme value distribution and computer implementation [J].Journal of Hebei Normal University(Natural Science Edition),2006,30(6):643-646.尚英姿,安润秋.极值分布的极大似然估计及计算机实现[J].河北师范大学学报(自然科学版),2006,30(6):643-646.

[13] GUMBEL E J.Statistical theory of extreme values and some practical applications[M].US:National Bureau of Standards,1954.

[14] ZHOU A X,ZHANG X N.The use of optimized fitting method in hydrological frequency analysis[J].Yangtze River,2007,38(6):38-39.周爱霞,张行南.优化适线法在水文频率分析中的应用[J].人民长江,2007,38(6):38-39.

[15] CHEN S J,YU J Y.Numerical solution of extreme wind speed advantage fitting and parameters of weibull distribution[J].Haiyang Xue bao,1987,9(3):302-310.陈上及,于继业.威布尔分布对风速年极值的拟合优势及其参数的数值解法[J].海洋学报,1987,9(3):302-310.

[16] Shanghai Typhoon Institute.Typhoon basic data set of the northwestern Pacific(1981—1988)[M].Beijing:China Meteorological Press, 1984.上海台风研究所.西北太平洋台风基本资料集(1949-1980)[M].北京:气象出版社,1984.

[17] China Meteorological Administration.Typhnoon yearbook[M].Beijing:Meteorological Press,1989-2014.中国气象局.台风年鉴[M].北京:气象出版社,1981-1988.

[18] China Meteogological Administration.Tropical cyclone yearbook[M].Beijing:Meteorological Press,1989-2014.中国气象局.热带气旋年鉴[M].北京:气象出版社,1989-2014.

[19] YANG T Z,YING R F.The study on the typhoon surge in the regions of Zhejiang islands[J].Marine Forecasts,1997,14(2):28-43.羊天柱,应仁方.浙江海岛风暴潮研究[J].海洋预报,1997,14(2):28-43.

[20] LIANG H S.Diagnostic analysis on track and precipitation of typhoon Molave[J].Advances in Marine Science,2011,29(1):28-36.梁宏升.台风“莫拉菲”移动路径和降水诊断分析[J].海洋科学进展,2011,29(1):28-36.

[21] HOU S M,SUN Z X.Analysis of“9711”typhoon track[J].Coastal Engineering,1998,17(2):63-69.侯淑梅,孙忠欣.9711号台风的路径分析与预报[J].海岸工程,1998,17(2):63-69.

[22] LU Y B,MA L F.The main character of super typhoon No.0608(SAOMAI)and characteristics analysis of its storm surge[J].Marine Forecasts,2007,24(4):92-96.卢益炳,马林芳.0608号超强台风“桑美”的主要特点和风暴潮影响特征分析[J].海洋预报,2007,24(4): 92-96.

Extreme Wind Speed and Return Period of Tropical Cyclones Passing Through Zhejiang Coastal Area

LIU Tian-tian1,WANG Yi-hang1,2,PEI Jun-feng3,MEI Qiu-ying1
(1.Faculty of Science,Ningbo University,Ningbo 315211,China; 2.Ningbo Collaborative Innovation Center of Nonlinear Hazard System of Ocean and Atmosphere,Ningbo 315211,China; 3.East Sea Information Center,SOA,Shanghai 200136,China)

The return period of extreme wind speed is not only an important parameter for coastal engineering,but also an critical index of forecast or early warning released by marine forecasting divisions.This paper analyzes extreme wind speed of the tropical cyclones passing through Zhejiang coastal area during 1949 -2015,and uses curve-fitting method based on moment of P-III distribution and Gumbel distribution to calculate the return periods of the extreme wind speed.The fitting curve of P-III distribution is better than that of Gumbel distribution according to the least square method,and can better fit the measurements. Comparing the results based on the two distributions,we found that the results of P-III distribution are more closer to the measurements,and according to this method the hundred year extreme wind speed is 92. 26 m/s.In addition,with application of Matrix Laboratory(Matlab),this study also gives the programming design for the calculation methods,which uses the self-adapting process to choose fitted curve.That is more objective and valid than the empirical fitting on the calculation method and in the operation way.

extreme wind speed;P-III distribution;Gumbel distribution;return period

P425

A

1671-6647(2017)01-0107-10

10.3969/j.issn.1671-6647.2017.01.011

2016-04-20

中国海洋工程咨询协会项目——沿海大型工程海洋灾害风险排查(宁波大榭岛石化集中区)(HS2015000171);国家海洋局海洋减灾中心项目——漫滩溃决水流与近岸建筑物的相互作用规律研究(HX2016000010)

刘甜甜(1991-),女,河南漯河人,硕士研究生,主要从事海洋数值模拟方面研究.E-mail:tiantianliu1991@163.com

*通讯作者:汪一航(1963-),男,浙江富阳人,副教授,博士,主要从事海洋潮流潮汐计算与海洋灾害风险评估方面的研究. E-mail:wangyihang@nbu.edu.cn

Received:April 20,2016